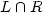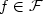Refine search
Actions for selected content:
48585 results in Computer Science
Maximal circular codes versus maximal codes
-
- Journal:
- RAIRO - Theoretical Informatics and Applications / Volume 35 / Issue 4 / July 2001
- Published online by Cambridge University Press:
- 15 April 2002, pp. 351-365
- Print publication:
- July 2001
-
- Article
- Export citation
Atoms and partial orders of infinite languages
-
- Journal:
- RAIRO - Theoretical Informatics and Applications / Volume 35 / Issue 4 / July 2001
- Published online by Cambridge University Press:
- 15 April 2002, pp. 389-401
- Print publication:
- July 2001
-
- Article
- Export citation
Automata-based Representations for Infinite Graphs
-
- Journal:
- RAIRO - Theoretical Informatics and Applications / Volume 35 / Issue 4 / July 2001
- Published online by Cambridge University Press:
- 15 April 2002, pp. 311-330
- Print publication:
- July 2001
-
- Article
- Export citation
On the expressive power of the shuffle operator matched with intersection by regular sets
-
- Journal:
- RAIRO - Theoretical Informatics and Applications / Volume 35 / Issue 4 / July 2001
- Published online by Cambridge University Press:
- 15 April 2002, pp. 379-388
- Print publication:
- July 2001
-
- Article
- Export citation
Towards parametrizing word equations
-
- Journal:
- RAIRO - Theoretical Informatics and Applications / Volume 35 / Issue 4 / July 2001
- Published online by Cambridge University Press:
- 15 April 2002, pp. 331-350
- Print publication:
- July 2001
-
- Article
- Export citation
The Helping Hierarchy
-
- Journal:
- RAIRO - Theoretical Informatics and Applications / Volume 35 / Issue 4 / July 2001
- Published online by Cambridge University Press:
- 15 April 2002, pp. 367-377
- Print publication:
- July 2001
-
- Article
- Export citation
2 - Models
-
- Book:
- Modal Logic
- Published online:
- 05 July 2014
- Print publication:
- 28 June 2001, pp 50-122
-
- Chapter
- Export citation
3 - Frames
-
- Book:
- Modal Logic
- Published online:
- 05 July 2014
- Print publication:
- 28 June 2001, pp 123-187
-
- Chapter
- Export citation
Appendix B - An Algebraic Toolkit
-
- Book:
- Modal Logic
- Published online:
- 05 July 2014
- Print publication:
- 28 June 2001, pp 497-503
-
- Chapter
- Export citation
Preface
-
- Book:
- Modal Logic
- Published online:
- 05 July 2014
- Print publication:
- 28 June 2001, pp xi-xxii
-
- Chapter
- Export citation
References
-
- Book:
- Modal Logic
- Published online:
- 05 July 2014
- Print publication:
- 28 June 2001, pp 524-543
-
- Chapter
- Export citation
Contents
-
- Book:
- Modal Logic
- Published online:
- 05 July 2014
- Print publication:
- 28 June 2001, pp vii-x
-
- Chapter
- Export citation
4 - Completeness
-
- Book:
- Modal Logic
- Published online:
- 05 July 2014
- Print publication:
- 28 June 2001, pp 188-260
-
- Chapter
- Export citation
Dedication
-
- Book:
- Modal Logic
- Published online:
- 05 July 2014
- Print publication:
- 28 June 2001, pp v-vi
-
- Chapter
- Export citation
Appendix D - A Guide to the Literature
-
- Book:
- Modal Logic
- Published online:
- 05 July 2014
- Print publication:
- 28 June 2001, pp 516-523
-
- Chapter
- Export citation
6 - Computability and Complexity
-
- Book:
- Modal Logic
- Published online:
- 05 July 2014
- Print publication:
- 28 June 2001, pp 332-412
-
- Chapter
- Export citation
5 - Algebras and General Frames
-
- Book:
- Modal Logic
- Published online:
- 05 July 2014
- Print publication:
- 28 June 2001, pp 261-331
-
- Chapter
- Export citation