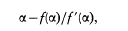Refine search
Actions for selected content:
13588 results in History of science and technology
Marcello Pera and William R. Shea (eds). Persuading Science: The Art of Scientific Rhetoric. Canton, MA: Science History Publications, 1991. Pp. xi + 212. ISBN 0-88135-071-0. $39.95.
-
- Journal:
- The British Journal for the History of Science / Volume 25 / Issue 3 / September 1992
- Published online by Cambridge University Press:
- 05 January 2009, pp. 387-388
- Print publication:
- September 1992
-
- Article
- Export citation
Karl Hufbauer. Exploring The Sun: Solar Science since Galileo. Baltimore: Johns Hopkins University Press, 1991. Pp. xv + 370. ISBN 0-8018-4098-8. £28.50, $46.00.
-
- Journal:
- The British Journal for the History of Science / Volume 25 / Issue 3 / September 1992
- Published online by Cambridge University Press:
- 05 January 2009, pp. 383-384
- Print publication:
- September 1992
-
- Article
- Export citation
William Aspray. John von Neumann and the Origins of Modern Computing. Cambridge, Mass, and London: MIT Press, 1991. Pp. xvii + 376. ISBN 0-262-01121-2. £31.50.
-
- Journal:
- The British Journal for the History of Science / Volume 25 / Issue 3 / September 1992
- Published online by Cambridge University Press:
- 05 January 2009, pp. 386-387
- Print publication:
- September 1992
-
- Article
- Export citation
Bill Luckin. Questions of Power: Electricity and Environment in Inter-War Britain. Manchester and New York: Manchester University Press, 1990. Pp. viii + 200. ISBN 0-7190-3302-0. £29.95.
-
- Journal:
- The British Journal for the History of Science / Volume 25 / Issue 3 / September 1992
- Published online by Cambridge University Press:
- 05 January 2009, pp. 378-379
- Print publication:
- September 1992
-
- Article
- Export citation
Thomas Simpson and ‘Newton's method of approximation’: an enduring myth
-
- Journal:
- The British Journal for the History of Science / Volume 25 / Issue 3 / September 1992
- Published online by Cambridge University Press:
- 05 January 2009, pp. 347-354
- Print publication:
- September 1992
-
- Article
- Export citation
-
A resurgence of interest has occurred in ‘Newton's method of approximation’ for deriving the roots of equations, as its repetitive and mechanical character permits ready computer use. If x = α is an approximate root of the equation f(x) = 0, then the method will in most cases give a better approximation as
where f′(x) is the derivative of the function into which α has been substituted. Older books sometimes called it ‘the Newton–Raphson method’, although the method was invented essentially in the above form by Thomas Simpson, who published his account of the method in 1740. However, as if through a time-warp, this invention has migrated back in time and is now matter-of-factly placed by historians in Newton's De analysi of 1669. This paper will describe the steps of this curious historical transposition, and speculate as to its cause.
F. Abbri and F. Crispini (eds.). Atti del IIIe Convegno Nazionale di Storia e Fondamenti della Chimica. Cosenza: Brenner editore, 1991. Pp. 402. L. 35,000.
-
- Journal:
- The British Journal for the History of Science / Volume 25 / Issue 3 / September 1992
- Published online by Cambridge University Press:
- 05 January 2009, pp. 372-373
- Print publication:
- September 1992
-
- Article
- Export citation
Milton Wainwright. Miracle Cure: The Story of Penicillin and the Golden Age of Antibiotics. Oxford: Basil Blackwell, 1990. Pp. xi + 196. ISBN 0-631-16492-8. £16.95.
-
- Journal:
- The British Journal for the History of Science / Volume 25 / Issue 3 / September 1992
- Published online by Cambridge University Press:
- 05 January 2009, pp. 376-377
- Print publication:
- September 1992
-
- Article
- Export citation
G. E. R. Lloyd. Methods and Problems in Greek Science: Selected Papers. Cambridge: Cambridge University Press, 1991. Pp. xiv + 457. ISBN 0-521-37419-7. £45.00, $59.50.
-
- Journal:
- The British Journal for the History of Science / Volume 25 / Issue 3 / September 1992
- Published online by Cambridge University Press:
- 05 January 2009, pp. 357-358
- Print publication:
- September 1992
-
- Article
- Export citation
E. B. Adams. In Search of Truth: A Portrait of Don Craib. London: Royal Society of Medicine Services, 1989. Pp. xii + 123, illus. ISBN 1-85315-119-X, £12.95 (hardback); 1-85315-118-1, £7.95 (paperback).
-
- Journal:
- The British Journal for the History of Science / Volume 25 / Issue 2 / June 1992
- Published online by Cambridge University Press:
- 05 January 2009, pp. 285-286
- Print publication:
- June 1992
-
- Article
- Export citation
Tore Frängsmyr (ed.). Solomon's House Revisited: The Organization and Institutionalization of Science. Canton, Mass.: Science History Publications (USA), 1990. Pp. xiii + 350. ISBN 0-88135-066-4. $49.50 (USA & Canada), $54.00 (elsewhere).
-
- Journal:
- The British Journal for the History of Science / Volume 25 / Issue 2 / June 1992
- Published online by Cambridge University Press:
- 05 January 2009, pp. 291-292
- Print publication:
- June 1992
-
- Article
- Export citation
David B. Wilson (ed.). The Correspondence Between Sir George Gabriel Stokes and Sir William Thomson, Baron Kelvin of Largs. Volume 1: 1846–1869; Volume 2: 1870–1901. Cambridge: Cambridge University Press, 1990. Pp. lvi + ix + 783. ISBN 0-521-32831-4. £125.00, $195.00.
-
- Journal:
- The British Journal for the History of Science / Volume 25 / Issue 2 / June 1992
- Published online by Cambridge University Press:
- 05 January 2009, pp. 278-279
- Print publication:
- June 1992
-
- Article
- Export citation
Lucille B. Ritvo. Darwin's Influence on Freud: A Tale of Two Sciences. New Haven and London: Yale University Press, 1990. pp. xii + 267. ISBN 0-300-04131-4. £19.95, $35.00.
-
- Journal:
- The British Journal for the History of Science / Volume 25 / Issue 2 / June 1992
- Published online by Cambridge University Press:
- 05 January 2009, pp. 280-281
- Print publication:
- June 1992
-
- Article
- Export citation
Ilana Löwy (ed.). The Polish School of Philosophy of Medicine: From Tytus Chalubinski (1820–1889) to Ludwik Fleck (1896–1961). Compiled, translated and with introductions by the editor. Dordrecht: Kluwer, 1990. Pp. viii + 287. ISBN 0-7923-0958-8. £44.00, $78.00, Dfl. 130.00.
-
- Journal:
- The British Journal for the History of Science / Volume 25 / Issue 2 / June 1992
- Published online by Cambridge University Press:
- 05 January 2009, pp. 281-282
- Print publication:
- June 1992
-
- Article
- Export citation
Richard L. Kremer. The Thermodynamics of Life and Experimental Physiology, 1770–1880. New York and London: Garland Publishing, 1990. Pp. xii + 512. ISBN 0-8240-0039-0. $50.00.
-
- Journal:
- The British Journal for the History of Science / Volume 25 / Issue 2 / June 1992
- Published online by Cambridge University Press:
- 05 January 2009, pp. 274-275
- Print publication:
- June 1992
-
- Article
- Export citation
Kameshwar C. Wall. Chandra: A Biography of S. Chandrasekhar. Chicago: University of Chicago Press, 1991. Pp. x + 341, illust. ISBN 0-226-87054-5. $34.50.
-
- Journal:
- The British Journal for the History of Science / Volume 25 / Issue 2 / June 1992
- Published online by Cambridge University Press:
- 05 January 2009, pp. 287-288
- Print publication:
- June 1992
-
- Article
- Export citation
J. W. Boag, P. W. Rubinin and D. Shoenberg (eds.). Kapitza in Cambridge and Moscow: Life and Letters of a Russian Physicist. Amsterdam: Elsevier Science, 1990. Pp. xvi + 429, illus. ISBN 0-444-98753, $77.00, Dfl. 150.00 (hardback); 0-444-98749-5; $38.00, Dfl. 75.00 (paperback).
-
- Journal:
- The British Journal for the History of Science / Volume 25 / Issue 2 / June 1992
- Published online by Cambridge University Press:
- 05 January 2009, pp. 286-287
- Print publication:
- June 1992
-
- Article
- Export citation
Adrian Desmond. The Politics of Evolution. Morphology, Medicine, and Reform in Radical London. Chicago and London: The University of Chicago Press, 1989. Pp. x + 503. ISBN 0-226-14346-5. £27.95.
-
- Journal:
- The British Journal for the History of Science / Volume 25 / Issue 2 / June 1992
- Published online by Cambridge University Press:
- 05 January 2009, pp. 275-278
- Print publication:
- June 1992
-
- Article
- Export citation
Geological thrusting
-
- Journal:
- The British Journal for the History of Science / Volume 25 / Issue 2 / June 1992
- Published online by Cambridge University Press:
- 05 January 2009, pp. 241-246
- Print publication:
- June 1992
-
- Article
- Export citation
Michael Eckert and Helmut Schubert. Crystals, Electrons, Transistors: From Scholar's Study to Industrial Research, translated by Thomas Hughes. New York: American Institute of Physics, 1990. Pp. xxii + 241. ISBN 0-88318-622-5, £45 (hardback); 0-88318-719-1, £15 (paperback).
-
- Journal:
- The British Journal for the History of Science / Volume 25 / Issue 2 / June 1992
- Published online by Cambridge University Press:
- 05 January 2009, pp. 288-289
- Print publication:
- June 1992
-
- Article
- Export citation
J. A. Bennett. Church, State and Astronomy in Ireland: 200 Years of Armagh Observatory. Armagh and Belfast: Armagh Observatory in association with The Institute of Irish Studies, The Queen's University of Belfast, 1990. Pp. vi + 277. ISBN (hardback) 0-9504478-1-1 (Armagh Observatory); 0-85389-350-0 (Queen's University). ISBN (paperback) 0-9504478-2-X (Armagh Observatory); 0-85389-351-9 (Queen's University). £17.95 (hardback).
-
- Journal:
- The British Journal for the History of Science / Volume 25 / Issue 2 / June 1992
- Published online by Cambridge University Press:
- 05 January 2009, p. 284
- Print publication:
- June 1992
-
- Article
- Export citation
