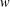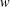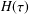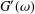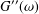Refine search
Actions for selected content:
8124 results in Fluid dynamics and solid mechanics
7 - Critical Flow Venturi Nozzle
-
- Book:
- Flow Measurement Handbook
- Published online:
- 05 August 2016
- Print publication:
- 25 August 2016, pp 177-194
-
- Chapter
- Export citation
4 - Calibration
-
- Book:
- Flow Measurement Handbook
- Published online:
- 05 August 2016
- Print publication:
- 25 August 2016, pp 67-115
-
- Chapter
- Export citation
ANZ VOLUME 58 ISSUE 1 COVER AND BACK MATTER
-
- Journal:
- The ANZIAM Journal / Volume 58 / Issue 1 / July 2016
- Published online by Cambridge University Press:
- 15 August 2016, pp. b1-b4
-
- Article
-
- You have access
- Export citation
ANZ VOLUME 58 ISSUE 1 COVER AND FRONT MATTER
-
- Journal:
- The ANZIAM Journal / Volume 58 / Issue 1 / July 2016
- Published online by Cambridge University Press:
- 15 August 2016, pp. f1-f2
-
- Article
-
- You have access
- Export citation

Flow Measurement Handbook
- Industrial Designs, Operating Principles, Performance, and Applications
-
- Published online:
- 05 August 2016
- Print publication:
- 25 August 2016
ON THE ALGEBRAIC PROPERTIES OF THE HUMAN ABO-BLOOD GROUP INHERITANCE PATTERN
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 58 / Issue 1 / July 2016
- Published online by Cambridge University Press:
- 21 July 2016, pp. 78-95
-
- Article
-
- You have access
- Export citation
UNSTEADY TWO-LAYERED BLOOD FLOW THROUGH A
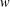 $w$ -SHAPED STENOSED ARTERY USING THE GENERALIZED OLDROYD-B FLUID MODEL
$w$ -SHAPED STENOSED ARTERY USING THE GENERALIZED OLDROYD-B FLUID MODEL
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 58 / Issue 1 / July 2016
- Published online by Cambridge University Press:
- 21 July 2016, pp. 96-118
-
- Article
-
- You have access
- Export citation
DIRECT EXPRESSION OF INCOMPATIBILITY IN CURVILINEAR SYSTEMS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 58 / Issue 1 / July 2016
- Published online by Cambridge University Press:
- 08 July 2016, pp. 33-50
-
- Article
-
- You have access
- Export citation
SIMPLE JOINT INVERSION LOCALIZED FORMULAE FOR RELAXATION SPECTRUM RECOVERY
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 58 / Issue 1 / July 2016
- Published online by Cambridge University Press:
- 05 July 2016, pp. 1-9
-
- Article
-
- You have access
- Export citation
THE COST–TIME CURVE FOR AN OPTIMAL TRAIN JOURNEY ON LEVEL TRACK
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 58 / Issue 1 / July 2016
- Published online by Cambridge University Press:
- 01 July 2016, pp. 10-32
-
- Article
-
- You have access
- Export citation
PERFORMANCE OF A REAL CODED GENETIC ALGORITHM FOR THE CALIBRATION OF SCALAR CONSERVATION LAWS
-
- Journal:
- The ANZIAM Journal / Volume 58 / Issue 1 / July 2016
- Published online by Cambridge University Press:
- 01 July 2016, pp. 51-77
-
- Article
-
- You have access
- Export citation
Contributors
-
- Book:
- Coarse Grained Simulation and Turbulent Mixing
- Published online:
- 05 June 2016
- Print publication:
- 30 June 2016, pp ix-x
-
- Chapter
- Export citation
12 - Spray Combustion in Swirling Flow
- from Part III - Complex Mixing Consequences
-
-
- Book:
- Coarse Grained Simulation and Turbulent Mixing
- Published online:
- 05 June 2016
- Print publication:
- 30 June 2016, pp 351-392
-
- Chapter
- Export citation
Index
-
- Book:
- Coarse Grained Simulation and Turbulent Mixing
- Published online:
- 05 June 2016
- Print publication:
- 30 June 2016, pp 443-444
-
- Chapter
- Export citation
4 - Material Conservation of Passive Scalar Mixing in Finite Scale Navier Stokes Fluid Turbulence
- from Part I - Fundamentals
-
-
- Book:
- Coarse Grained Simulation and Turbulent Mixing
- Published online:
- 05 June 2016
- Print publication:
- 30 June 2016, pp 87-104
-
- Chapter
- Export citation
9 - Laser Driven Turbulence in High Energy Density Physics and Inertial Confinement Fusion Experiments
- from Part III - Complex Mixing Consequences
-
-
- Book:
- Coarse Grained Simulation and Turbulent Mixing
- Published online:
- 05 June 2016
- Print publication:
- 30 June 2016, pp 232-281
-
- Chapter
- Export citation
Preface
-
- Book:
- Coarse Grained Simulation and Turbulent Mixing
- Published online:
- 05 June 2016
- Print publication:
- 30 June 2016, pp xi-xii
-
- Chapter
- Export citation
Prologue
-
-
- Book:
- Coarse Grained Simulation and Turbulent Mixing
- Published online:
- 05 June 2016
- Print publication:
- 30 June 2016, pp 1-12
-
- Chapter
- Export citation
10 - Drive Asymmetry, Convergence, and the Origin of Turbulence in Inertial Confinement Fusion Implosions
- from Part III - Complex Mixing Consequences
-
-
- Book:
- Coarse Grained Simulation and Turbulent Mixing
- Published online:
- 05 June 2016
- Print publication:
- 30 June 2016, pp 282-324
-
- Chapter
- Export citation
8 - Shock Driven Turbulence
- from Part III - Complex Mixing Consequences
-
-
- Book:
- Coarse Grained Simulation and Turbulent Mixing
- Published online:
- 05 June 2016
- Print publication:
- 30 June 2016, pp 193-231
-
- Chapter
- Export citation