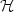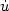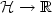Refine search
Actions for selected content:
6997 results in Mathematical modeling and methods
Probabilistic methods for semilinearpartial differential equations.Applications to finance
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 44 / Issue 5 / September 2010
- Published online by Cambridge University Press:
- 26 August 2010, pp. 1107-1133
- Print publication:
- September 2010
-
- Article
- Export citation
Existence, uniqueness and convergence of a particle approximation for the AdaptiveBiasing Force process
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 44 / Issue 5 / September 2010
- Published online by Cambridge University Press:
- 26 August 2010, pp. 831-865
- Print publication:
- September 2010
-
- Article
- Export citation
Stochastic Lagrangian method for downscaling problemsin computational fluid dynamics
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 44 / Issue 5 / September 2010
- Published online by Cambridge University Press:
- 26 August 2010, pp. 885-920
- Print publication:
- September 2010
-
- Article
- Export citation
Trend to equilibrium and particle approximation for a weakly selfconsistent Vlasov-Fokker-Planck equation
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 44 / Issue 5 / September 2010
- Published online by Cambridge University Press:
- 26 August 2010, pp. 867-884
- Print publication:
- September 2010
-
- Article
- Export citation
Low-variance direct Monte Carlo simulationsusing importance weights
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 44 / Issue 5 / September 2010
- Published online by Cambridge University Press:
- 26 August 2010, pp. 1069-1083
- Print publication:
- September 2010
-
- Article
- Export citation
Numerical algorithms for backward stochasticdifferential equations with 1-d brownian motion:Convergence and simulations* **
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 45 / Issue 2 / March 2011
- Published online by Cambridge University Press:
- 24 August 2010, pp. 335-360
- Print publication:
- March 2011
-
- Article
- Export citation
On the null-controllability of diffusion equations
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 17 / Issue 4 / October 2011
- Published online by Cambridge University Press:
- 23 August 2010, pp. 1088-1100
- Print publication:
- October 2011
-
- Article
- Export citation
Optimality conditions for semilinear parabolic equations withcontrols in leading term*
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 17 / Issue 4 / October 2011
- Published online by Cambridge University Press:
- 23 August 2010, pp. 975-994
- Print publication:
- October 2011
-
- Article
- Export citation
Optimized Schwarz coupling of Bidomainand Monodomain models in electrocardiology
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 45 / Issue 2 / March 2011
- Published online by Cambridge University Press:
- 20 August 2010, pp. 309-334
- Print publication:
- March 2011
-
- Article
- Export citation
A null controllability data assimilation methodologyapplied to a large scale ocean circulation model*
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 45 / Issue 2 / March 2011
- Published online by Cambridge University Press:
- 20 August 2010, pp. 361-386
- Print publication:
- March 2011
-
- Article
- Export citation
Solving the Cahn-Hilliard variational inequalitywith a semi-smooth Newton method
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 17 / Issue 4 / October 2011
- Published online by Cambridge University Press:
- 18 August 2010, pp. 931-954
- Print publication:
- October 2011
-
- Article
- Export citation
Analytical results on a model for damagingin domains and interfaces*
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 17 / Issue 4 / October 2011
- Published online by Cambridge University Press:
- 18 August 2010, pp. 955-974
- Print publication:
- October 2011
-
- Article
- Export citation
Convergence and regularization resultsfor optimal control problems with sparsity functional
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 17 / Issue 3 / July 2011
- Published online by Cambridge University Press:
- 06 August 2010, pp. 858-886
- Print publication:
- July 2011
-
- Article
- Export citation
Deterministic state-constrained optimal control problems without controllability assumptions
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 17 / Issue 4 / October 2011
- Published online by Cambridge University Press:
- 06 August 2010, pp. 995-1015
- Print publication:
- October 2011
-
- Article
- Export citation
Complete asymptotic expansions for eigenvaluesofDirichlet Laplacian in thin three-dimensional rods*
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 17 / Issue 3 / July 2011
- Published online by Cambridge University Press:
- 06 August 2010, pp. 887-908
- Print publication:
- July 2011
-
- Article
- Export citation
Numerical analysis of some optimal control problemsgoverned by a class of quasilinear elliptic equations*
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 17 / Issue 3 / July 2011
- Published online by Cambridge University Press:
- 06 August 2010, pp. 771-800
- Print publication:
- July 2011
-
- Article
- Export citation
Logarithmic decay of the energyfor an hyperbolic-parabolic coupled system
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 17 / Issue 3 / July 2011
- Published online by Cambridge University Press:
- 06 August 2010, pp. 801-835
- Print publication:
- July 2011
-
- Article
- Export citation
Variational approximation for detectingpoint-like target problems*
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 17 / Issue 4 / October 2011
- Published online by Cambridge University Press:
- 06 August 2010, pp. 909-930
- Print publication:
- October 2011
-
- Article
- Export citation
Numerical solution of an inverse initial boundary value problem forthe wave equation in the presenceof conductivity imperfections ofsmall volume
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 17 / Issue 4 / October 2011
- Published online by Cambridge University Press:
- 06 August 2010, pp. 1016-1034
- Print publication:
- October 2011
-
- Article
- Export citation
Asymptotic behavior of second-order dissipative evolution equations combining potential with non-potential effects*
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 17 / Issue 3 / July 2011
- Published online by Cambridge University Press:
- 06 August 2010, pp. 836-857
- Print publication:
- July 2011
-
- Article
- Export citation