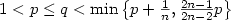Refine search
Actions for selected content:
6997 results in Mathematical modeling and methods
2 - First-Order and Simple Higher-Order Differential Equations
-
- Book:
- Differential Equations for Engineers
- Published online:
- 05 June 2012
- Print publication:
- 26 April 2010, pp 16-86
-
- Chapter
- Export citation
Appendix A - Tables of Mathematical Formulas
-
- Book:
- Differential Equations for Engineers
- Published online:
- 05 June 2012
- Print publication:
- 26 April 2010, pp 531-541
-
- Chapter
- Export citation
1 - Introduction
-
- Book:
- Differential Equations for Engineers
- Published online:
- 05 June 2012
- Print publication:
- 26 April 2010, pp 1-15
-
- Chapter
- Export citation
Frontmatter
-
- Book:
- Differential Equations for Engineers
- Published online:
- 05 June 2012
- Print publication:
- 26 April 2010, pp i-vi
-
- Chapter
- Export citation
4 - Linear Differential Equations
-
- Book:
- Differential Equations for Engineers
- Published online:
- 05 June 2012
- Print publication:
- 26 April 2010, pp 140-187
-
- Chapter
- Export citation
5 - Applications of Linear Differential Equations
-
- Book:
- Differential Equations for Engineers
- Published online:
- 05 June 2012
- Print publication:
- 26 April 2010, pp 188-243
-
- Chapter
- Export citation
9 - Series Solutions of Differential Equations
-
- Book:
- Differential Equations for Engineers
- Published online:
- 05 June 2012
- Print publication:
- 26 April 2010, pp 390-430
-
- Chapter
- Export citation
3 - Applications of First-Order and Simple Higher-Order Equations
-
- Book:
- Differential Equations for Engineers
- Published online:
- 05 June 2012
- Print publication:
- 26 April 2010, pp 87-139
-
- Chapter
- Export citation
8 - Applications of Systems of Linear Differential Equations
-
- Book:
- Differential Equations for Engineers
- Published online:
- 05 June 2012
- Print publication:
- 26 April 2010, pp 357-389
-
- Chapter
- Export citation
Preface
-
- Book:
- Differential Equations for Engineers
- Published online:
- 05 June 2012
- Print publication:
- 26 April 2010, pp xiii-xvi
-
- Chapter
- Export citation
Contents
-
- Book:
- Differential Equations for Engineers
- Published online:
- 05 June 2012
- Print publication:
- 26 April 2010, pp vii-xii
-
- Chapter
- Export citation
10 - Numerical Solutions of Differential Equations
-
- Book:
- Differential Equations for Engineers
- Published online:
- 05 June 2012
- Print publication:
- 26 April 2010, pp 431-456
-
- Chapter
- Export citation
7 - Systems of Linear Differential Equations
-
- Book:
- Differential Equations for Engineers
- Published online:
- 05 June 2012
- Print publication:
- 26 April 2010, pp 300-356
-
- Chapter
- Export citation
Higher-order phase transitions with line-tension effect
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 17 / Issue 3 / July 2011
- Published online by Cambridge University Press:
- 23 April 2010, pp. 603-647
- Print publication:
- July 2011
-
- Article
- Export citation
Nonlinear dynamic systems and optimal control problems on time scales*
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 17 / Issue 3 / July 2011
- Published online by Cambridge University Press:
- 23 April 2010, pp. 654-681
- Print publication:
- July 2011
-
- Article
- Export citation
Partial regularity of minimizers of higher order integrals with (p, q)-growth
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 17 / Issue 2 / April 2011
- Published online by Cambridge University Press:
- 23 April 2010, pp. 472-492
- Print publication:
- April 2011
-
- Article
- Export citation
Analysis of a time optimal control problem relatedto the management of a bioreactor***
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 17 / Issue 3 / July 2011
- Published online by Cambridge University Press:
- 23 April 2010, pp. 722-748
- Print publication:
- July 2011
-
- Article
- Export citation
Strong unique continuation for the Lamé system with Lipschitz coefficients in three dimensions*
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 17 / Issue 3 / July 2011
- Published online by Cambridge University Press:
- 23 April 2010, pp. 761-770
- Print publication:
- July 2011
-
- Article
- Export citation
Feedback stabilization of a boundary layer equation: Part 1: Homogeneous state equations*
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 17 / Issue 2 / April 2011
- Published online by Cambridge University Press:
- 23 April 2010, pp. 506-551
- Print publication:
- April 2011
-
- Article
- Export citation
Stochastic differential games involving impulse controls*
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 17 / Issue 3 / July 2011
- Published online by Cambridge University Press:
- 23 April 2010, pp. 749-760
- Print publication:
- July 2011
-
- Article
- Export citation