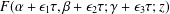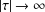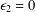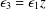Refine search
Actions for selected content:
6997 results in Mathematical modeling and methods
10 - Should I Take This Drug for My Headache?
-
- Book:
- Quantitative Reasoning
- Published online:
- 21 September 2020
- Print publication:
- 16 January 2020, pp 143-156
-
- Chapter
- Export citation
8 - Why Is It Dark at Night?
-
- Book:
- Quantitative Reasoning
- Published online:
- 21 September 2020
- Print publication:
- 16 January 2020, pp 113-130
-
- Chapter
- Export citation
Preface
-
- Book:
- Quantitative Reasoning
- Published online:
- 21 September 2020
- Print publication:
- 16 January 2020, pp ix-xii
-
- Chapter
- Export citation
Frontmatter
-
- Book:
- Quantitative Reasoning
- Published online:
- 21 September 2020
- Print publication:
- 16 January 2020, pp i-iv
-
- Chapter
- Export citation
Skills Assessments
-
- Book:
- Quantitative Reasoning
- Published online:
- 21 September 2020
- Print publication:
- 16 January 2020, pp 222-228
-
- Chapter
- Export citation
1 - Is College Worth the Cost?
-
- Book:
- Quantitative Reasoning
- Published online:
- 21 September 2020
- Print publication:
- 16 January 2020, pp 1-20
-
- Chapter
- Export citation
5 - What Is the Economic Impact of the Undocumented?
-
- Book:
- Quantitative Reasoning
- Published online:
- 21 September 2020
- Print publication:
- 16 January 2020, pp 61-80
-
- Chapter
- Export citation
Index
-
- Book:
- Quantitative Reasoning
- Published online:
- 21 September 2020
- Print publication:
- 16 January 2020, pp 237-242
-
- Chapter
- Export citation
Acknowledgements
-
- Book:
- Quantitative Reasoning
- Published online:
- 21 September 2020
- Print publication:
- 16 January 2020, pp xiii-xiii
-
- Chapter
- Export citation
7 - Can We Recycle Pollution?
-
- Book:
- Quantitative Reasoning
- Published online:
- 21 September 2020
- Print publication:
- 16 January 2020, pp 97-112
-
- Chapter
- Export citation
9 - Where Do the Stars Go in the Daytime?
-
- Book:
- Quantitative Reasoning
- Published online:
- 21 September 2020
- Print publication:
- 16 January 2020, pp 131-142
-
- Chapter
- Export citation
6 - Should I Buy Health Insurance?
-
- Book:
- Quantitative Reasoning
- Published online:
- 21 September 2020
- Print publication:
- 16 January 2020, pp 81-96
-
- Chapter
- Export citation
Glossary
-
- Book:
- Quantitative Reasoning
- Published online:
- 21 September 2020
- Print publication:
- 16 January 2020, pp 229-236
-
- Chapter
- Export citation
Introduction
-
- Book:
- Quantitative Reasoning
- Published online:
- 21 September 2020
- Print publication:
- 16 January 2020, pp xiv-xviii
-
- Chapter
- Export citation
Appendices
-
- Book:
- Quantitative Reasoning
- Published online:
- 21 September 2020
- Print publication:
- 16 January 2020, pp 157-221
-
- Chapter
- Export citation
2 - How Many People Died in the Civil War?
-
- Book:
- Quantitative Reasoning
- Published online:
- 21 September 2020
- Print publication:
- 16 January 2020, pp 21-34
-
- Chapter
- Export citation
3 - How Much Will This Car Cost?
-
- Book:
- Quantitative Reasoning
- Published online:
- 21 September 2020
- Print publication:
- 16 January 2020, pp 35-46
-
- Chapter
- Export citation
Contents
-
- Book:
- Quantitative Reasoning
- Published online:
- 21 September 2020
- Print publication:
- 16 January 2020, pp v-viii
-
- Chapter
- Export citation
4 - Should We Worry about Arsenic in Rice?
-
- Book:
- Quantitative Reasoning
- Published online:
- 21 September 2020
- Print publication:
- 16 January 2020, pp 47-60
-
- Chapter
- Export citation
ASYMPTOTICS OF A GAUSS HYPERGEOMETRIC FUNCTION WITH TWO LARGE PARAMETERS: A NEW CASE
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 62 / Issue 4 / October 2020
- Published online by Cambridge University Press:
- 10 December 2019, pp. 446-452
-
- Article
-
- You have access
- Export citation