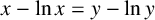Refine search
Actions for selected content:
6993 results in Mathematical modeling and methods
ANALYTICAL APPROXIMATIONS OF LOTKA–VOLTERRA INTEGRALS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 67 / 2025
- Published online by Cambridge University Press:
- 02 April 2025, e10
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
DYNAMICAL ANALYSIS OF A PARAMETRICALLY FORCED MAGNETO-MECHANICAL OSCILLATOR
-
- Journal:
- The ANZIAM Journal / Volume 67 / 2025
- Published online by Cambridge University Press:
- 02 April 2025, e15
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ANALYSIS OF A DISCRETIZED FRACTIONAL-ORDER PREY–PREDATOR MODEL UNDER WIND EFFECT
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 67 / 2025
- Published online by Cambridge University Press:
- 02 April 2025, e9
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ESTIMATION OF MEAN SQUARED ERRORS OF NON-BINARY A/D ENCODERS THROUGH FREDHOLM DETERMINANTS OF PIECEWISE-LINEAR TRANSFORMATIONS II: GENERAL CASE
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 67 / 2025
- Published online by Cambridge University Press:
- 19 March 2025, e14
-
- Article
- Export citation
MICRO-MACRO PARAREAL, FROM ORDINARY DIFFERENTIAL EQUATIONS TO STOCHASTIC DIFFERENTIAL EQUATIONS AND BACK AGAIN
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 67 / 2025
- Published online by Cambridge University Press:
- 17 March 2025, e13
-
- Article
- Export citation
A SIXTH-ORDER HERMITE COLLOCATION TECHNIQUE FOR NUMERICAL STUDY OF NONLINEAR FISHER AND BURGERS–FISHER EQUATIONS
-
- Journal:
- The ANZIAM Journal / Volume 67 / 2025
- Published online by Cambridge University Press:
- 14 March 2025, e12
-
- Article
- Export citation
CONFORMAL IMAGE REGISTRATION USING THE DISCRETIZED CAUCHY–RIEMANN EQUATIONS
-
- Journal:
- The ANZIAM Journal / Volume 67 / 2025
- Published online by Cambridge University Press:
- 18 February 2025, e8
-
- Article
- Export citation
INDEX
-
- Journal:
- The ANZIAM Journal / Volume 66 / Issue 4 / October 2024
- Published online by Cambridge University Press:
- 12 February 2025, pp. 285-286
-
- Article
- Export citation
EARLY WARNING PREDICTION WITH AUTOMATIC LABELLING IN EPILEPSY PATIENTS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 67 / 2025
- Published online by Cambridge University Press:
- 27 January 2025, e4
-
- Article
- Export citation
NONLINEAR MODULATION OF RANDOM WAVE SPECTRA FOR SURFACE-GRAVITY WAVES WITH LINEAR SHEAR CURRENTS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 66 / Issue 4 / October 2024
- Published online by Cambridge University Press:
- 10 January 2025, pp. 222-237
-
- Article
- Export citation
OPTIMAL CONTROL PROBLEMS GOVERNED BY MARGUERRE–VON KÁRMÁN EQUATIONS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 67 / 2025
- Published online by Cambridge University Press:
- 01 January 2025, e38
-
- Article
- Export citation
DISSIPATION OF WAVE ENERGY AND MITIGATION OF WAVE FORCE BY MULTIPLE FLEXIBLE POROUS PLATES
-
- Journal:
- The ANZIAM Journal / Volume 66 / Issue 4 / October 2024
- Published online by Cambridge University Press:
- 26 December 2024, pp. 258-284
-
- Article
- Export citation
SYMMETRY RESTORATION IN COLLISIONS OF SOLITONS IN FRACTIONAL COUPLERS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 67 / 2025
- Published online by Cambridge University Press:
- 03 December 2024, e7
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
HARMONIC RESONANCE OF SHORT-CRESTED GRAVITY WAVES ON DEEP WATER: ON THEIR PERSISTENCY
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 67 / 2025
- Published online by Cambridge University Press:
- 03 December 2024, e1
-
- Article
- Export citation
FURTHER ACCURACY VERIFICATION OF A 2D ADAPTIVE MESH REFINEMENT METHOD USING STEADY FLOW PAST A SQUARE CYLINDER
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 67 / 2025
- Published online by Cambridge University Press:
- 19 November 2024, e3
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
AN INVESTIGATION ON NONLINEAR OPTION PRICING BEHAVIOURS THROUGH A NEW FRÉCHET DERIVATIVE-BASED QUADRATURE APPROACH
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 66 / Issue 4 / October 2024
- Published online by Cambridge University Press:
- 15 November 2024, pp. 238-257
-
- Article
- Export citation
STABILITY ANALYSIS FOR STOCHASTIC MCKEAN–VLASOV EQUATION
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 67 / 2025
- Published online by Cambridge University Press:
- 06 November 2024, e6
-
- Article
- Export citation
ON WELL-POSED BOUNDARY CONDITIONS AND ENERGY STABLE FINITE-VOLUME METHOD FOR THE LINEAR SHALLOW WATER WAVE EQUATION
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 66 / Issue 3 / July 2024
- Published online by Cambridge University Press:
- 22 October 2024, pp. 181-200
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
EFFECT OF NONUNIFORM POROSITY IN CURVED BREAKWATER ON WATER WAVES
-
- Journal:
- The ANZIAM Journal / Volume 66 / Issue 3 / July 2024
- Published online by Cambridge University Press:
- 21 October 2024, pp. 201-221
-
- Article
- Export citation
IRROTATIONAL FLOW DUE TO FORCED OSCILLATIONS OF A BUBBLE
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 66 / Issue 3 / July 2024
- Published online by Cambridge University Press:
- 18 October 2024, pp. 152-180
-
- Article
-
- You have access
- Open access
- HTML
- Export citation