Refine search
Actions for selected content:
6993 results in Mathematical modeling and methods
IMPLICIT–EXPLICIT TIME INTEGRATION METHOD FOR FRACTIONAL ADVECTION–DIFFUSION-REACTION EQUATIONS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 67 / 2025
- Published online by Cambridge University Press:
- 16 October 2024, e2
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
EFFECT OF EXTERNAL HARMONIC VIBRATION ON THE FORMATION OF SOLITARY WAVES IN FALLING TWO-LAYER LIQUID FILMS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 67 / 2025
- Published online by Cambridge University Press:
- 16 October 2024, e5
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
PRODUCTION OPTIMIZATION FOR AGENTS OF DIFFERING WORK RATES
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 66 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 24 September 2024, pp. 98-120
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
EMBED IN ENSEMBLE TO RIGOROUSLY AND ACCURATELY HOMOGENIZE QUASI-PERIODIC MULTI-SCALE HETEROGENEOUS MATERIAL
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 66 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 19 September 2024, pp. 1-34
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ANALYTICALLY PRICING EUROPEAN OPTIONS UNDER A TWO-FACTOR STOCHASTIC INTEREST RATE MODEL WITH A STOCHASTIC LONG-RUN EQUILIBRIUM LEVEL
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 66 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 19 September 2024, pp. 132-151
-
- Article
- Export citation
SPECTRAL CLUSTERING AND LONG TIMESERIES CLASSIFICATION
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 66 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 18 September 2024, pp. 121-131
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
CAPILLARY LEVELLING OF THIN LIQUID FILMS OF POWER-LAW RHEOLOGY
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 66 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 16 September 2024, pp. 62-76
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
METHODOLOGY AND CHALLENGES OF SURROGATE MODELLING METHODS FOR MULTI-FIDELITY EXPENSIVE BLACK-BOX PROBLEMS
-
- Journal:
- The ANZIAM Journal / Volume 66 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 31 May 2024, pp. 35-61
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
17 - Linear Equations II
-
- Book:
- Mathematics for Economics and Finance
- Published online:
- 24 May 2024
- Print publication:
- 30 May 2024, pp 173-189
-
- Chapter
- Export citation
28 - Second-Order Differential Equations
-
- Book:
- Mathematics for Economics and Finance
- Published online:
- 24 May 2024
- Print publication:
- 30 May 2024, pp 319-333
-
- Chapter
- Export citation
6 - Introduction to Calculus
-
- Book:
- Mathematics for Economics and Finance
- Published online:
- 24 May 2024
- Print publication:
- 30 May 2024, pp 51-60
-
- Chapter
- Export citation
9 - The Derivative in Economics I
-
- Book:
- Mathematics for Economics and Finance
- Published online:
- 24 May 2024
- Print publication:
- 30 May 2024, pp 85-92
-
- Chapter
- Export citation
13 - Optimisation in Two Variables
-
- Book:
- Mathematics for Economics and Finance
- Published online:
- 24 May 2024
- Print publication:
- 30 May 2024, pp 123-136
-
- Chapter
- Export citation
20 - Determinants
-
- Book:
- Mathematics for Economics and Finance
- Published online:
- 24 May 2024
- Print publication:
- 30 May 2024, pp 212-223
-
- Chapter
- Export citation
Dedication
-
- Book:
- Mathematics for Economics and Finance
- Published online:
- 24 May 2024
- Print publication:
- 30 May 2024, pp v-vi
-
- Chapter
- Export citation
30 - Applications of Diagonalisation
-
- Book:
- Mathematics for Economics and Finance
- Published online:
- 24 May 2024
- Print publication:
- 30 May 2024, pp 347-360
-
- Chapter
- Export citation
19 - The Input–Output Model
-
- Book:
- Mathematics for Economics and Finance
- Published online:
- 24 May 2024
- Print publication:
- 30 May 2024, pp 204-211
-
- Chapter
- Export citation
10 - The Derivative in Economics II
-
- Book:
- Mathematics for Economics and Finance
- Published online:
- 24 May 2024
- Print publication:
- 30 May 2024, pp 93-100
-
- Chapter
- Export citation
Index
-
- Book:
- Mathematics for Economics and Finance
- Published online:
- 24 May 2024
- Print publication:
- 30 May 2024, pp 416-421
-
- Chapter
- Export citation
24 - Macroeconomic Applications
-
- Book:
- Mathematics for Economics and Finance
- Published online:
- 24 May 2024
- Print publication:
- 30 May 2024, pp 264-273
-
- Chapter
- Export citation
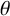
 ) and the Zimm chain solution (
) and the Zimm chain solution ( ). Numerical simulations of the viscoelastic channel flow effectively capture the nonhomogeneous regions of high viscosity at low fluid inertia (or the so-called “spatiotemporal macrostructures”), experimentally observed in the flow-instability transition of subdiffusive flows.
). Numerical simulations of the viscoelastic channel flow effectively capture the nonhomogeneous regions of high viscosity at low fluid inertia (or the so-called “spatiotemporal macrostructures”), experimentally observed in the flow-instability transition of subdiffusive flows.