Refine search
Actions for selected content:
6993 results in Mathematical modeling and methods
ANZ VOLUME 57 ISSUE 2 COVER AND FRONT MATTER
-
- Journal:
- The ANZIAM Journal / Volume 57 / Issue 2 / October 2015
- Published online by Cambridge University Press:
- 17 December 2015, pp. f1-f2
-
- Article
-
- You have access
- Export citation
NUMERICAL STABILITY AND ACCURACY OF THE SCALED BOUNDARY FINITE ELEMENT METHOD IN ENGINEERING APPLICATIONS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 57 / Issue 2 / October 2015
- Published online by Cambridge University Press:
- 17 December 2015, pp. 114-137
-
- Article
-
- You have access
- Export citation

Doing the Scholarship of Teaching and Learning in Mathematics
-
- Published by:
- Mathematical Association of America
- Published online:
- 05 December 2015
- Print publication:
- 15 December 2014
-
- Book
- Export citation
A CELL GROWTH MODEL ADAPTED FOR THE MINIMUM CELL SIZE DIVISION
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 57 / Issue 2 / October 2015
- Published online by Cambridge University Press:
- 01 December 2015, pp. 138-149
-
- Article
-
- You have access
- Export citation

Partial Differential Equation Methods for Image Inpainting
-
- Published online:
- 05 November 2015
- Print publication:
- 26 October 2015
HETEROGENEOUS SYSTEMS IN
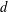 $d$ DIMENSIONS: LOWER SPECTRUM
$d$ DIMENSIONS: LOWER SPECTRUM
-
- Journal:
- The ANZIAM Journal / Volume 57 / Issue 2 / October 2015
- Published online by Cambridge University Press:
- 03 November 2015, pp. 150-165
-
- Article
-
- You have access
- Export citation
7 - The Mumford-Shah Image Model for Inpainting
-
- Book:
- Partial Differential Equation Methods for Image Inpainting
- Published online:
- 05 November 2015
- Print publication:
- 26 October 2015, pp 161-173
-
- Chapter
- Export citation
3 - The Principle of Good Continuation
-
- Book:
- Partial Differential Equation Methods for Image Inpainting
- Published online:
- 05 November 2015
- Print publication:
- 26 October 2015, pp 26-31
-
- Chapter
- Export citation
Appendix C - MATLAB Implementation
-
- Book:
- Partial Differential Equation Methods for Image Inpainting
- Published online:
- 05 November 2015
- Print publication:
- 26 October 2015, pp 229-230
-
- Chapter
- Export citation
Frontmatter
-
- Book:
- Partial Differential Equation Methods for Image Inpainting
- Published online:
- 05 November 2015
- Print publication:
- 26 October 2015, pp i-iv
-
- Chapter
- Export citation
1 - Introduction
-
- Book:
- Partial Differential Equation Methods for Image Inpainting
- Published online:
- 05 November 2015
- Print publication:
- 26 October 2015, pp 1-7
-
- Chapter
- Export citation
Preface
-
- Book:
- Partial Differential Equation Methods for Image Inpainting
- Published online:
- 05 November 2015
- Print publication:
- 26 October 2015, pp ix-x
-
- Chapter
- Export citation
References
-
- Book:
- Partial Differential Equation Methods for Image Inpainting
- Published online:
- 05 November 2015
- Print publication:
- 26 October 2015, pp 237-252
-
- Chapter
- Export citation
6 - Transport Inpainting
-
- Book:
- Partial Differential Equation Methods for Image Inpainting
- Published online:
- 05 November 2015
- Print publication:
- 26 October 2015, pp 137-160
-
- Chapter
- Export citation
4 - Second-Order Diffusion Equations for Inpainting
-
- Book:
- Partial Differential Equation Methods for Image Inpainting
- Published online:
- 05 November 2015
- Print publication:
- 26 October 2015, pp 32-62
-
- Chapter
- Export citation
Contents
-
- Book:
- Partial Differential Equation Methods for Image Inpainting
- Published online:
- 05 November 2015
- Print publication:
- 26 October 2015, pp vii-viii
-
- Chapter
- Export citation
Dedication
-
- Book:
- Partial Differential Equation Methods for Image Inpainting
- Published online:
- 05 November 2015
- Print publication:
- 26 October 2015, pp v-vi
-
- Chapter
- Export citation
Appendix D - Image Credits
-
- Book:
- Partial Differential Equation Methods for Image Inpainting
- Published online:
- 05 November 2015
- Print publication:
- 26 October 2015, pp 231-232
-
- Chapter
- Export citation
Appendix B - Mathematical Preliminaries
-
- Book:
- Partial Differential Equation Methods for Image Inpainting
- Published online:
- 05 November 2015
- Print publication:
- 26 October 2015, pp 217-228
-
- Chapter
- Export citation
Index
-
- Book:
- Partial Differential Equation Methods for Image Inpainting
- Published online:
- 05 November 2015
- Print publication:
- 26 October 2015, pp 253-254
-
- Chapter
- Export citation