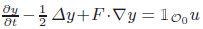Refine search
Actions for selected content:
6993 results in Mathematical modeling and methods
Constant Versus Periodic Fishing: Age Structured OptimalControl Approach
-
- Journal:
- Mathematical Modelling of Natural Phenomena / Volume 9 / Issue 4 / 2014
- Published online by Cambridge University Press:
- 20 June 2014, pp. 20-37
- Print publication:
- 2014
-
- Article
- Export citation
Preface
-
- Journal:
- Mathematical Modelling of Natural Phenomena / Volume 9 / Issue 2 / 2014
- Published online by Cambridge University Press:
- 24 April 2014, pp. 1-3
- Print publication:
- 2014
-
- Article
- Export citation
CMV Matrices with Super Exponentially Decaying VerblunskyCoefficients
-
- Journal:
- Mathematical Modelling of Natural Phenomena / Volume 9 / Issue 5 / 2014
- Published online by Cambridge University Press:
- 17 July 2014, pp. 282-294
- Print publication:
- 2014
-
- Article
- Export citation
Coupling Vector-host Dynamics with Weather Geography andMitigation Measures to Model Rift Valley Fever in Africa
-
- Journal:
- Mathematical Modelling of Natural Phenomena / Volume 9 / Issue 2 / 2014
- Published online by Cambridge University Press:
- 24 April 2014, pp. 161-177
- Print publication:
- 2014
-
- Article
- Export citation
Linear Size-structured Population Models with Spacial Diffusion and Optimal Harvesting Problems
-
- Journal:
- Mathematical Modelling of Natural Phenomena / Volume 9 / Issue 4 / 2014
- Published online by Cambridge University Press:
- 20 June 2014, pp. 122-130
- Print publication:
- 2014
-
- Article
- Export citation
Preface
-
- Journal:
- Mathematical Modelling of Natural Phenomena / Volume 9 / Issue 4 / 2014
- Published online by Cambridge University Press:
- 20 June 2014, pp. 1-5
- Print publication:
- 2014
-
- Article
- Export citation
Preface
-
- Journal:
- Mathematical Modelling of Natural Phenomena / Volume 9 / Issue 1 / 2014
- Published online by Cambridge University Press:
- 07 February 2014, pp. 1-3
- Print publication:
- 2014
-
- Article
- Export citation
Diffusion and Deterministic Systems
-
- Journal:
- Mathematical Modelling of Natural Phenomena / Volume 9 / Issue 1 / 2014
- Published online by Cambridge University Press:
- 07 February 2014, pp. 139-150
- Print publication:
- 2014
-
- Article
- Export citation
Tridiagonal Substitution Hamiltonians
-
- Journal:
- Mathematical Modelling of Natural Phenomena / Volume 9 / Issue 5 / 2014
- Published online by Cambridge University Press:
- 17 July 2014, pp. 204-238
- Print publication:
- 2014
-
- Article
- Export citation
Variational approximation of a functional of Mumford–Shah typein codimension higher than one
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 20 / Issue 1 / January 2014
- Published online by Cambridge University Press:
- 27 January 2014, pp. 190-221
- Print publication:
- January 2014
-
- Article
- Export citation
Patient Specific Haemodynamic Modeling after OcclusionTreatment in Leg
-
- Journal:
- Mathematical Modelling of Natural Phenomena / Volume 9 / Issue 6 / 2014
- Published online by Cambridge University Press:
- 31 July 2014, pp. 85-97
- Print publication:
- 2014
-
- Article
- Export citation
Inverse Scattering Problem with UnderdeterminedData
-
- Journal:
- Mathematical Modelling of Natural Phenomena / Volume 9 / Issue 5 / 2014
- Published online by Cambridge University Press:
- 17 July 2014, pp. 244-253
- Print publication:
- 2014
-
- Article
- Export citation
Exact null internal controllability for the heat equation on unbounded convex domains∗
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 20 / Issue 1 / January 2014
- Published online by Cambridge University Press:
- 27 January 2014, pp. 222-235
- Print publication:
- January 2014
-
- Article
- Export citation
Modelling Biological Evolution: Introduction to the SpecialIssue
-
- Journal:
- Mathematical Modelling of Natural Phenomena / Volume 9 / Issue 3 / 2014
- Published online by Cambridge University Press:
- 28 May 2014, pp. 1-4
- Print publication:
- 2014
-
- Article
-
- You have access
- Export citation
Optimal Control of Leukemic Cell PopulationDynamics
-
- Journal:
- Mathematical Modelling of Natural Phenomena / Volume 9 / Issue 1 / 2014
- Published online by Cambridge University Press:
- 07 February 2014, pp. 4-26
- Print publication:
- 2014
-
- Article
- Export citation
Optimal Vaccination, Treatment, and Preventive Campaigns inRegard to the SIR Epidemic Model
-
- Journal:
- Mathematical Modelling of Natural Phenomena / Volume 9 / Issue 4 / 2014
- Published online by Cambridge University Press:
- 20 June 2014, pp. 105-121
- Print publication:
- 2014
-
- Article
- Export citation
Blood Flow Simulation Using Traceless Variant ofJohnson-Segalman Viscoelastic Model
-
- Journal:
- Mathematical Modelling of Natural Phenomena / Volume 9 / Issue 6 / 2014
- Published online by Cambridge University Press:
- 24 September 2014, pp. 117-141
- Print publication:
- 2014
-
- Article
- Export citation
Controllability of 3D low Reynolds numberswimmers
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 20 / Issue 1 / January 2014
- Published online by Cambridge University Press:
- 27 January 2014, pp. 236-268
- Print publication:
- January 2014
-
- Article
- Export citation
Spectral Analysis of the Efficiency of Vertical Mixing in theDeep Ocean due to Interaction of Tidal Currents with a Ridge Running down a ContinentalSlope
-
- Journal:
- Mathematical Modelling of Natural Phenomena / Volume 9 / Issue 5 / 2014
- Published online by Cambridge University Press:
- 17 July 2014, pp. 119-137
- Print publication:
- 2014
-
- Article
- Export citation
Toward a General Model for the Evolution of DNA Replication inThree Domains of Life
-
- Journal:
- Mathematical Modelling of Natural Phenomena / Volume 9 / Issue 3 / 2014
- Published online by Cambridge University Press:
- 28 May 2014, pp. 96-106
- Print publication:
- 2014
-
- Article
- Export citation