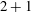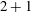Refine search
Actions for selected content:
6993 results in Mathematical modeling and methods
THREE-DIMENSIONAL WAVE-FREE POTENTIALS IN THE THEORY OF WATER WAVES
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 55 / Issue 2 / October 2013
- Published online by Cambridge University Press:
- 18 March 2014, pp. 175-195
-
- Article
-
- You have access
- Export citation
ANZ VOLUME 55 ISSUE 2 COVER AND BACK MATTER
-
- Journal:
- The ANZIAM Journal / Volume 55 / Issue 2 / October 2013
- Published online by Cambridge University Press:
- 18 March 2014, pp. b1-b11
-
- Article
-
- You have access
- Export citation
AN OPTIMAL DIVIDEND POLICY WITH DELAYED CAPITAL INJECTIONS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 55 / Issue 2 / October 2013
- Published online by Cambridge University Press:
- 18 March 2014, pp. 129-150
-
- Article
-
- You have access
- Export citation
ANZ VOLUME 55 ISSUE 2 COVER AND FRONT MATTER
-
- Journal:
- The ANZIAM Journal / Volume 55 / Issue 2 / October 2013
- Published online by Cambridge University Press:
- 18 March 2014, pp. f1-f2
-
- Article
-
- You have access
- Export citation
BLOW-UP OF THE NONEQUIVARIANT (
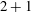 $2+1$)-DIMENSIONAL WAVE MAP
$2+1$)-DIMENSIONAL WAVE MAP
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 55 / Issue 2 / October 2013
- Published online by Cambridge University Press:
- 18 March 2014, pp. 151-161
-
- Article
-
- You have access
- Export citation
BIASED RANDOM WALKS, PARTIAL DIFFERENTIAL EQUATIONS AND UPDATE SCHEMES
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 55 / Issue 2 / October 2013
- Published online by Cambridge University Press:
- 18 March 2014, pp. 93-108
-
- Article
-
- You have access
- Export citation
A CARTOPT METHOD FOR BOUND-CONSTRAINED GLOBAL OPTIMIZATION
-
- Journal:
- The ANZIAM Journal / Volume 55 / Issue 2 / October 2013
- Published online by Cambridge University Press:
- 18 March 2014, pp. 109-128
-
- Article
-
- You have access
- Export citation
Adaptive stabilization of coupled PDE–ODE systems with multipleuncertainties∗
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 20 / Issue 2 / April 2014
- Published online by Cambridge University Press:
- 14 March 2014, pp. 488-516
- Print publication:
- April 2014
-
- Article
- Export citation
Second-order sufficient conditions for strong solutions to optimal control problems∗
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 20 / Issue 3 / July 2014
- Published online by Cambridge University Press:
- 14 March 2014, pp. 704-724
- Print publication:
- July 2014
-
- Article
- Export citation
Minimising convex combinations of low eigenvalues∗
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 20 / Issue 2 / April 2014
- Published online by Cambridge University Press:
- 07 March 2014, pp. 442-459
- Print publication:
- April 2014
-
- Article
- Export citation
A certified reduced basis method for parametrized ellipticoptimal control problems∗
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 20 / Issue 2 / April 2014
- Published online by Cambridge University Press:
- 07 March 2014, pp. 416-441
- Print publication:
- April 2014
-
- Article
- Export citation
Regularity results for an optimal design problem with a volumeconstraint
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 20 / Issue 2 / April 2014
- Published online by Cambridge University Press:
- 07 March 2014, pp. 460-487
- Print publication:
- April 2014
-
- Article
- Export citation
Multiplicity and concentration behavior of positive solutionsfor a Schrödinger–Kirchhoff type problem via penalization method∗∗∗
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 20 / Issue 2 / April 2014
- Published online by Cambridge University Press:
- 03 March 2014, pp. 389-415
- Print publication:
- April 2014
-
- Article
- Export citation
Global minimizer of the ground state for two phase conductorsin low contrast regime∗∗∗
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 20 / Issue 2 / April 2014
- Published online by Cambridge University Press:
- 03 March 2014, pp. 362-388
- Print publication:
- April 2014
-
- Article
- Export citation
Polyharmonic homogenization, rough polyharmonic splines and sparse super-localization
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 48 / Issue 2 / March 2014
- Published online by Cambridge University Press:
- 11 March 2014, pp. 517-552
- Print publication:
- March 2014
-
- Article
- Export citation
Machine Computation Using the Exponentially Convergent Multiscale Spectral Generalized Finite Element Method∗
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 48 / Issue 2 / March 2014
- Published online by Cambridge University Press:
- 11 March 2014, pp. 493-515
- Print publication:
- March 2014
-
- Article
- Export citation
A Multiscale Enrichment Procedure for Nonlinear Monotone Operators
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 48 / Issue 2 / March 2014
- Published online by Cambridge University Press:
- 11 March 2014, pp. 475-491
- Print publication:
- March 2014
-
- Article
- Export citation
Corrector Analysis of a Heterogeneous Multi-scale Scheme forElliptic Equations with Random Potential
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 48 / Issue 2 / March 2014
- Published online by Cambridge University Press:
- 20 February 2014, pp. 387-409
- Print publication:
- March 2014
-
- Article
- Export citation
A Multiscale Model Reduction Method for Partial DifferentialEquations
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 48 / Issue 2 / March 2014
- Published online by Cambridge University Press:
- 20 February 2014, pp. 449-474
- Print publication:
- March 2014
-
- Article
- Export citation
Sweeping preconditioners for elastic wave propagation withspectral element methods
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 48 / Issue 2 / March 2014
- Published online by Cambridge University Press:
- 20 February 2014, pp. 433-447
- Print publication:
- March 2014
-
- Article
- Export citation