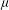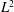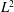Refine search
Actions for selected content:
6997 results in Mathematical modeling and methods
MODELLING OF RESISTIVE PULSE SENSING: FLEXIBLE METHODS FOR SUBMICRON PARTICLES
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 55 / Issue 3 / January 2014
- Published online by Cambridge University Press:
- 06 June 2014, pp. 197-213
-
- Article
-
- You have access
- Export citation
EXACT SOLUTIONS FOR INTERFACIAL OUTFLOWS WITH STRAINING
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 55 / Issue 3 / January 2014
- Published online by Cambridge University Press:
- 05 June 2014, pp. 232-244
-
- Article
-
- You have access
- Export citation
Dirichlet control of unsteady Navier–Stokes type system related to Soret convection by boundary penalty method
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 20 / Issue 3 / July 2014
- Published online by Cambridge University Press:
- 05 June 2014, pp. 840-863
- Print publication:
- July 2014
-
- Article
- Export citation
OPTIMAL
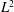 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}L^2$ ESTIMATES FOR THE SEMIDISCRETE GALERKIN METHOD APPLIED TO PARABOLIC INTEGRO-DIFFERENTIAL EQUATIONS WITH NONSMOOTH DATA
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}L^2$ ESTIMATES FOR THE SEMIDISCRETE GALERKIN METHOD APPLIED TO PARABOLIC INTEGRO-DIFFERENTIAL EQUATIONS WITH NONSMOOTH DATA
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 55 / Issue 3 / January 2014
- Published online by Cambridge University Press:
- 05 June 2014, pp. 245-266
-
- Article
-
- You have access
- Export citation
New regularity results and improved error estimates for optimal control problems with state constraints∗
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 20 / Issue 3 / July 2014
- Published online by Cambridge University Press:
- 05 June 2014, pp. 803-822
- Print publication:
- July 2014
-
- Article
- Export citation
NEW DEVELOPMENT OF NONRIGID REGISTRATION
-
- Journal:
- The ANZIAM Journal / Volume 55 / Issue 3 / January 2014
- Published online by Cambridge University Press:
- 05 June 2014, pp. 289-297
-
- Article
-
- You have access
- Export citation
HOPF BIFURCATION ANALYSIS FOR A RATIO-DEPENDENT PREDATOR–PREY SYSTEM INVOLVING TWO DELAYS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 55 / Issue 3 / January 2014
- Published online by Cambridge University Press:
- 05 June 2014, pp. 214-231
-
- Article
-
- You have access
- Export citation

Complexity Science
- The Warwick Master's Course
-
- Published online:
- 05 June 2014
- Print publication:
- 21 November 2013
MEMBRANE-COUPLED GRAVITY WAVE SCATTERING BY A VERTICAL BARRIER WITH A GAP
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 55 / Issue 3 / January 2014
- Published online by Cambridge University Press:
- 05 June 2014, pp. 267-288
-
- Article
-
- You have access
- Export citation
Global Carleman estimate for stochastic parabolic equations, and its application∗
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 20 / Issue 3 / July 2014
- Published online by Cambridge University Press:
- 05 June 2014, pp. 823-839
- Print publication:
- July 2014
-
- Article
- Export citation
Control of underwater vehicles in inviscidfluids: I. Irrotational flows
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 20 / Issue 3 / July 2014
- Published online by Cambridge University Press:
- 27 May 2014, pp. 662-703
- Print publication:
- July 2014
-
- Article
- Export citation
Linearized plastic plate models as Γ-limits of 3D finiteelastoplasticity
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 20 / Issue 3 / July 2014
- Published online by Cambridge University Press:
- 27 May 2014, pp. 725-747
- Print publication:
- July 2014
-
- Article
- Export citation
Curve cuspless reconstruction via sub-Riemannian geometry∗∗∗
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 20 / Issue 3 / July 2014
- Published online by Cambridge University Press:
- 27 May 2014, pp. 748-770
- Print publication:
- July 2014
-
- Article
- Export citation
The value function representing Hamilton–Jacobi equation with Hamiltonian depending on value of solution
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 20 / Issue 3 / July 2014
- Published online by Cambridge University Press:
- 21 May 2014, pp. 771-802
- Print publication:
- July 2014
-
- Article
- Export citation
A deterministic affine-quadratic optimal control problem∗
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 20 / Issue 3 / July 2014
- Published online by Cambridge University Press:
- 21 May 2014, pp. 633-661
- Print publication:
- July 2014
-
- Article
- Export citation

The Finite-Difference Modelling of Earthquake Motions
- Waves and Ruptures
-
- Published online:
- 05 May 2014
- Print publication:
- 24 April 2014
Contents
-
- Book:
- The Finite-Difference Modelling of Earthquake Motions
- Published online:
- 05 May 2014
- Print publication:
- 24 April 2014, pp vii-xiv
-
- Chapter
- Export citation
The Finite-Difference Modelling of Earthquake Motions - Half title page
-
- Book:
- The Finite-Difference Modelling of Earthquake Motions
- Published online:
- 05 May 2014
- Print publication:
- 24 April 2014, pp i-i
-
- Chapter
- Export citation
Part IV - Finite-difference modelling of seismic motion at real sites
-
- Book:
- The Finite-Difference Modelling of Earthquake Motions
- Published online:
- 05 May 2014
- Print publication:
- 24 April 2014, pp 305-326
-
- Chapter
- Export citation
Acknowledgements
-
- Book:
- The Finite-Difference Modelling of Earthquake Motions
- Published online:
- 05 May 2014
- Print publication:
- 24 April 2014, pp xv-xvi
-
- Chapter
- Export citation