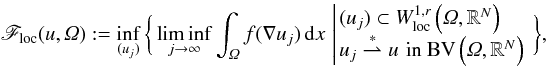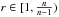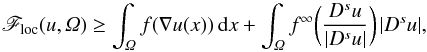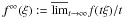Refine search
Actions for selected content:
6993 results in Mathematical modeling and methods
Monotone (A,B) entropy stable numerical scheme for ScalarConservation Laws with discontinuous flux
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 48 / Issue 6 / November 2014
- Published online by Cambridge University Press:
- 26 September 2014, pp. 1725-1755
- Print publication:
- November 2014
-
- Article
- Export citation
Highly anisotropic nonlinear temperature balance equation andits numerical solution using asymptotic-preserving schemes of second order in time ∗
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 48 / Issue 6 / November 2014
- Published online by Cambridge University Press:
- 26 September 2014, pp. 1701-1724
- Print publication:
- November 2014
-
- Article
- Export citation
Study of a low Mach nuclear core model for two-phase flows withphase transition I: stiffened gas law
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 48 / Issue 6 / November 2014
- Published online by Cambridge University Press:
- 24 September 2014, pp. 1639-1679
- Print publication:
- November 2014
-
- Article
- Export citation
The splitting in potential Crank–Nicolson scheme with discretetransparent boundary conditions for the Schrödinger equation on a semi-infinitestrip
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 48 / Issue 6 / November 2014
- Published online by Cambridge University Press:
- 24 September 2014, pp. 1681-1699
- Print publication:
- November 2014
-
- Article
- Export citation
EFFECTS OF TIME DELAY ON THE DYNAMICS OF A KINETIC MODEL OF A MICROBIAL FERMENTATION PROCESS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 55 / Issue 4 / April 2014
- Published online by Cambridge University Press:
- 10 September 2014, pp. 336-356
-
- Article
-
- You have access
- Export citation
ANZ VOLUME 55 ISSUE 4 COVER AND FRONT MATTER
-
- Journal:
- The ANZIAM Journal / Volume 55 / Issue 4 / April 2014
- Published online by Cambridge University Press:
- 10 September 2014, pp. f1-f2
-
- Article
-
- You have access
- Export citation
A CLOSED-FORM PRICING FORMULA FOR VARIANCE SWAPS WITH MEAN-REVERTING GAUSSIAN VOLATILITY
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 55 / Issue 4 / April 2014
- Published online by Cambridge University Press:
- 10 September 2014, pp. 362-382
-
- Article
-
- You have access
- Export citation
MOTION OF A SLIP SPHERE IN A NONCONCENTRIC FICTITIOUS SPHERICAL ENVELOPE OF MICROPOLAR FLUID
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 55 / Issue 4 / April 2014
- Published online by Cambridge University Press:
- 10 September 2014, pp. 383-401
-
- Article
-
- You have access
- Export citation
ANZ VOLUME 55 ISSUE 4 COVER AND BACK MATTER
-
- Journal:
- The ANZIAM Journal / Volume 55 / Issue 4 / April 2014
- Published online by Cambridge University Press:
- 10 September 2014, pp. b1-b7
-
- Article
-
- You have access
- Export citation
A Posteriori Error Estimation for ReducedOrder Solutions of Parametrized Parabolic Optimal Control Problems∗
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 48 / Issue 6 / November 2014
- Published online by Cambridge University Press:
- 09 September 2014, pp. 1615-1638
- Print publication:
- November 2014
-
- Article
- Export citation
A posteriori error estimates for ellipticproblems with Dirac measure terms in weighted spaces
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 48 / Issue 6 / November 2014
- Published online by Cambridge University Press:
- 09 September 2014, pp. 1557-1581
- Print publication:
- November 2014
-
- Article
- Export citation
Derivation of a homogenized two-temperature model from the heatequation
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 48 / Issue 6 / November 2014
- Published online by Cambridge University Press:
- 09 September 2014, pp. 1583-1613
- Print publication:
- November 2014
-
- Article
- Export citation
𝒞1,β regularity for Dirichlet problems associated to fully nonlineardegenerate elliptic equations
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 20 / Issue 4 / October 2014
- Published online by Cambridge University Press:
- 13 August 2014, pp. 1009-1024
- Print publication:
- October 2014
-
- Article
- Export citation
Error estimates for Stokes problem with Tresca frictionconditions
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 48 / Issue 5 / September 2014
- Published online by Cambridge University Press:
- 13 August 2014, pp. 1413-1429
- Print publication:
- September 2014
-
- Article
- Export citation
Measuring the Irreversibility of Numerical Schemes forReversible Stochastic Differential Equations∗
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 48 / Issue 5 / September 2014
- Published online by Cambridge University Press:
- 13 August 2014, pp. 1351-1379
- Print publication:
- September 2014
-
- Article
- Export citation
Mathematical analysis of a discrete fracture model couplingDarcy flow in the matrix with Darcy–Forchheimer flow in the fracture∗
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 48 / Issue 5 / September 2014
- Published online by Cambridge University Press:
- 13 August 2014, pp. 1451-1472
- Print publication:
- September 2014
-
- Article
- Export citation
Relaxation in BV of integrals with superlineargrowth
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 20 / Issue 4 / October 2014
- Published online by Cambridge University Press:
- 13 August 2014, pp. 1078-1122
- Print publication:
- October 2014
-
- Article
- Export citation
A localized orthogonal decomposition method for semi-linearelliptic problems∗∗∗
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 48 / Issue 5 / September 2014
- Published online by Cambridge University Press:
- 13 August 2014, pp. 1331-1349
- Print publication:
- September 2014
-
- Article
- Export citation
Adaptive mesh refinement strategy for a non conservativetransport problem∗
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 48 / Issue 5 / September 2014
- Published online by Cambridge University Press:
- 13 August 2014, pp. 1381-1412
- Print publication:
- September 2014
-
- Article
- Export citation
Scalar boundary value problems on junctions of thin rods andplates: I. Asymptotic analysis and error estimates
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 48 / Issue 5 / September 2014
- Published online by Cambridge University Press:
- 13 August 2014, pp. 1495-1528
- Print publication:
- September 2014
-
- Article
- Export citation