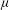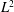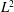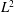Refine search
Actions for selected content:
6993 results in Mathematical modeling and methods
Convergence of mass redistribution method for theone-dimensional wave equation with a unilateral constraint at the boundary
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 48 / Issue 4 / July 2014
- Published online by Cambridge University Press:
- 08 July 2014, pp. 1147-1169
- Print publication:
- July 2014
-
- Article
- Export citation
Formal passage from kinetic theory to incompressible Navier–Stokes equations for a mixture of gases
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 48 / Issue 4 / July 2014
- Published online by Cambridge University Press:
- 15 July 2014, pp. 1171-1197
- Print publication:
- July 2014
-
- Article
- Export citation
A reduced model for Darcy’s problem in networks offractures∗
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 48 / Issue 4 / July 2014
- Published online by Cambridge University Press:
- 02 July 2014, pp. 1089-1116
- Print publication:
- July 2014
-
- Article
- Export citation
Basic principles of mixed Virtual Element Methods
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 48 / Issue 4 / July 2014
- Published online by Cambridge University Press:
- 15 July 2014, pp. 1227-1240
- Print publication:
- July 2014
-
- Article
- Export citation
Anisotropic mesh refinement in polyhedral domains: error estimates with data in L2(Ω)
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 48 / Issue 4 / July 2014
- Published online by Cambridge University Press:
- 04 July 2014, pp. 1117-1145
- Print publication:
- July 2014
-
- Article
- Export citation
ON THE ORGANIZATION OF ROUND ROBIN TOURNAMENTS WITH CONSTRAINTS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 55 / Issue 4 / April 2014
- Published online by Cambridge University Press:
- 01 July 2014, pp. 357-361
-
- Article
-
- You have access
- Export citation
An efficient computational framework for reducedbasis approximation and a posteriori error estimation of parametrized Navier–Stokes flows
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 48 / Issue 4 / July 2014
- Published online by Cambridge University Press:
- 15 July 2014, pp. 1199-1226
- Print publication:
- July 2014
-
- Article
- Export citation
A weighted empirical interpolation method: a prioriconvergence analysis and applications
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 48 / Issue 4 / July 2014
- Published online by Cambridge University Press:
- 30 June 2014, pp. 943-953
- Print publication:
- July 2014
-
- Article
- Export citation
Reconstruction of thickness variation of a dielectric coatingthrough the generalized impedance boundary conditions∗
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 48 / Issue 4 / July 2014
- Published online by Cambridge University Press:
- 30 June 2014, pp. 1011-1027
- Print publication:
- July 2014
-
- Article
- Export citation
A mixed formulation of a sharp interface model of stokes flow with moving contact lines∗
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 48 / Issue 4 / July 2014
- Published online by Cambridge University Press:
- 30 June 2014, pp. 969-1009
- Print publication:
- July 2014
-
- Article
- Export citation
A new quadrilateral MINI-element for Stokes equations
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 48 / Issue 4 / July 2014
- Published online by Cambridge University Press:
- 30 June 2014, pp. 955-968
- Print publication:
- July 2014
-
- Article
- Export citation
Analysis of a time discretization scheme for a nonstandardviscous Cahn–Hilliard system
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 48 / Issue 4 / July 2014
- Published online by Cambridge University Press:
- 30 June 2014, pp. 1061-1087
- Print publication:
- July 2014
-
- Article
- Export citation
High order semi-Lagrangian particle methodsfor transport equations:numerical analysis and implementation issues
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 48 / Issue 4 / July 2014
- Published online by Cambridge University Press:
- 30 June 2014, pp. 1029-1060
- Print publication:
- July 2014
-
- Article
- Export citation
On the Fattorini criterion for approximate controllability and stabilizability of parabolic systems
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 20 / Issue 3 / July 2014
- Published online by Cambridge University Press:
- 13 June 2014, pp. 924-956
- Print publication:
- July 2014
-
- Article
- Export citation
On the relation of delay equations to first-order hyperbolic partial differential equations
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 20 / Issue 3 / July 2014
- Published online by Cambridge University Press:
- 13 June 2014, pp. 894-923
- Print publication:
- July 2014
-
- Article
- Export citation
Riemannian metrics on 2D-manifolds related to the Euler−Poinsot rigid body motion∗
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 20 / Issue 3 / July 2014
- Published online by Cambridge University Press:
- 10 June 2014, pp. 864-893
- Print publication:
- July 2014
-
- Article
- Export citation
MODELLING OF RESISTIVE PULSE SENSING: FLEXIBLE METHODS FOR SUBMICRON PARTICLES
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 55 / Issue 3 / January 2014
- Published online by Cambridge University Press:
- 06 June 2014, pp. 197-213
-
- Article
-
- You have access
- Export citation
EXACT SOLUTIONS FOR INTERFACIAL OUTFLOWS WITH STRAINING
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 55 / Issue 3 / January 2014
- Published online by Cambridge University Press:
- 05 June 2014, pp. 232-244
-
- Article
-
- You have access
- Export citation
Dirichlet control of unsteady Navier–Stokes type system related to Soret convection by boundary penalty method
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 20 / Issue 3 / July 2014
- Published online by Cambridge University Press:
- 05 June 2014, pp. 840-863
- Print publication:
- July 2014
-
- Article
- Export citation
OPTIMAL
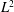 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}L^2$ ESTIMATES FOR THE SEMIDISCRETE GALERKIN METHOD APPLIED TO PARABOLIC INTEGRO-DIFFERENTIAL EQUATIONS WITH NONSMOOTH DATA
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}L^2$ ESTIMATES FOR THE SEMIDISCRETE GALERKIN METHOD APPLIED TO PARABOLIC INTEGRO-DIFFERENTIAL EQUATIONS WITH NONSMOOTH DATA
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 55 / Issue 3 / January 2014
- Published online by Cambridge University Press:
- 05 June 2014, pp. 245-266
-
- Article
-
- You have access
- Export citation