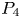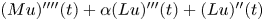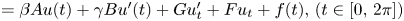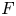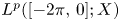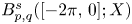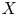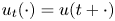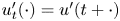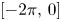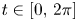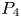Refine listing
Actions for selected content:
82 results in 34Kxx
Periodic dynamics of a general switching dynamical system
- Part of
-
- Journal:
- European Journal of Applied Mathematics , First View
- Published online by Cambridge University Press:
- 08 August 2025, pp. 1-15
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Optimal stopping zero-sum games in continuous hidden Markov models
- Part of
-
- Journal:
- Advances in Applied Probability , First View
- Published online by Cambridge University Press:
- 28 July 2025, pp. 1-44
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A DELAY DYNAMICAL SYSTEM’S PERSPECTIVE ON THE GLUCOSE–INSULIN REGULATORY RESPONSE TO ON–OFF GLUCOSE INFUSION
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 67 / 2025
- Published online by Cambridge University Press:
- 22 July 2025, e26
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Impact of prey-taxis on a harvested intraguild predation predator–prey model
- Part of
-
- Journal:
- European Journal of Applied Mathematics , First View
- Published online by Cambridge University Press:
- 10 March 2025, pp. 1-38
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Two dynamical approaches to the notion of exponential separation for random systems of delay differential equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 24 February 2025, pp. 1-39
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Hopf bifurcations for a delayed discrete single population patch model in advective environments
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 36 / Issue 4 / August 2025
- Published online by Cambridge University Press:
- 11 November 2024, pp. 705-737
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A diffusive plant-sulphide model: spatio-temporal dynamics contrast between discrete and distributed delay
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 36 / Issue 4 / August 2025
- Published online by Cambridge University Press:
- 28 October 2024, pp. 811-828
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The dynamical analysis of a nonlocal predator–prey model with cannibalism
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 35 / Issue 5 / October 2024
- Published online by Cambridge University Press:
- 29 January 2024, pp. 707-731
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Branching patterns of wave trains in mass-in-mass lattices
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 4 / August 2025
- Published online by Cambridge University Press:
- 11 January 2024, pp. 1240-1266
- Print publication:
- August 2025
-
- Article
- Export citation
Long-time dynamics and semi-wave of a delayed nonlocal epidemic model with free boundaries
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 05 October 2023, pp. 564-610
- Print publication:
- April 2025
-
- Article
- Export citation
Periodic solutions of four-order degenerate differential equations with finite delay in vector-valued function spaces
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 14 September 2023, pp. 395-412
- Print publication:
- April 2025
-
- Article
- Export citation
NOVEL STABILITY CONDITIONS FOR SOME GENERALIZATION OF NICHOLSON’S BLOWFLIES MODEL WITH STOCHASTIC PERTURBATIONS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 64 / Issue 4 / October 2022
- Published online by Cambridge University Press:
- 23 August 2023, pp. 394-405
-
- Article
- Export citation
Spreading dynamics of a diffusive epidemic model with free boundaries and two delays
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 34 / Issue 6 / December 2023
- Published online by Cambridge University Press:
- 11 August 2023, pp. 1133-1169
-
- Article
- Export citation
Local and global existence and uniqueness of solution for abstract differential equations with state-dependent argument
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 2 / May 2023
- Published online by Cambridge University Press:
- 26 April 2023, pp. 305-345
-
- Article
- Export citation
Dynamics of a delayed population patch model with the dispersion matrix incorporating population loss
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 34 / Issue 4 / August 2023
- Published online by Cambridge University Press:
- 21 March 2023, pp. 870-895
-
- Article
- Export citation
HOPF BIFURCATION ANALYSIS OF A FRACTIONAL-ORDER HOLLING–TANNER PREDATOR-PREY MODEL WITH TIME DELAY
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 64 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 05 April 2022, pp. 23-39
-
- Article
- Export citation
Convergence rate of the EM algorithm for SDEs with low regular drifts
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 14 February 2022, pp. 447-470
- Print publication:
- June 2022
-
- Article
- Export citation
On meromorphic solutions of functional-differential equations
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 10 February 2022, pp. 263-278
-
- Article
- Export citation
Conley index for manifold-valued retarded functional differential equations without uniqueness of solutions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 19 April 2021, pp. 428-449
- Print publication:
- April 2022
-
- Article
- Export citation
Exact simulation for multivariate Itô diffusions
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 52 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 03 December 2020, pp. 1003-1034
- Print publication:
- December 2020
-
- Article
- Export citation