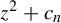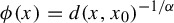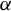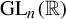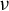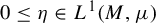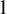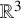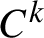Refine listing
Actions for selected content:
38 results in 37Hxx
Sub-additivity of measure theoretic entropies of commuting transformations on Banach spaces
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 10 July 2025, pp. 1-35
-
- Article
- Export citation
Mean topological dimension of a random dynamical system for amenable groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society , First View
- Published online by Cambridge University Press:
- 07 July 2025, pp. 1-32
-
- Article
- Export citation
Two dynamical approaches to the notion of exponential separation for random systems of delay differential equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 24 February 2025, pp. 1-39
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Asymptotic expansion of the invariant measure for Markov-modulated ODEs at high frequency
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 62 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 30 January 2025, pp. 898-924
- Print publication:
- September 2025
-
- Article
- Export citation
Geometric properties of disintegration of measures
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 5 / May 2025
- Published online by Cambridge University Press:
- 11 October 2024, pp. 1619-1648
- Print publication:
- May 2025
-
- Article
- Export citation
On the stochastic bifurcations regarding random iterations of polynomials of the form
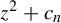 $z^{2} + c_{n}$
$z^{2} + c_{n}$
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 11 / November 2024
- Published online by Cambridge University Press:
- 26 February 2024, pp. 3358-3384
- Print publication:
- November 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Stable laws for random dynamical systems
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 11 / November 2024
- Published online by Cambridge University Press:
- 14 February 2024, pp. 3041-3090
- Print publication:
- November 2024
-
- Article
- Export citation
Random and mean Lyapunov exponents for
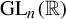 $\operatorname {\mathrm {GL}}_n(\mathbb {R})$
$\operatorname {\mathrm {GL}}_n(\mathbb {R})$
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 8 / August 2024
- Published online by Cambridge University Press:
- 11 December 2023, pp. 2063-2079
- Print publication:
- August 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Statistical determinism in non-Lipschitz dynamical systems
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 7 / July 2024
- Published online by Cambridge University Press:
- 11 October 2023, pp. 1856-1884
- Print publication:
- July 2024
-
- Article
- Export citation
On the quasi-ergodicity of absorbing Markov chains with unbounded transition densities, including random logistic maps with escape
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 7 / July 2024
- Published online by Cambridge University Press:
- 25 September 2023, pp. 1818-1855
- Print publication:
- July 2024
-
- Article
- Export citation
On the dimension of stationary measures for random piecewise affine interval homeomorphisms
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 6 / June 2024
- Published online by Cambridge University Press:
- 04 August 2023, pp. 1473-1488
- Print publication:
- June 2024
-
- Article
- Export citation
Weak random periodic solutions of random dynamical systems
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 12 July 2023, pp. 137-151
- Print publication:
- March 2024
-
- Article
- Export citation
Counting periodic orbits on fractals weighted by their Lyapounov exponents
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 3 / August 2023
- Published online by Cambridge University Press:
- 03 July 2023, pp. 710-757
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Beltrami fields exhibit knots and chaos almost surely
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 27 June 2023, e56
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The natural extension of the random beta-transformation
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 11 / November 2023
- Published online by Cambridge University Press:
- 04 November 2022, pp. 3861-3896
- Print publication:
- November 2023
-
- Article
- Export citation
Equilibrium states for non-transitive random open and closed dynamical systems
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 10 / October 2023
- Published online by Cambridge University Press:
- 13 October 2022, pp. 3193-3215
- Print publication:
- October 2023
-
- Article
- Export citation
Quenched and annealed equilibrium states for random Ruelle expanding maps and applications
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 9 / September 2023
- Published online by Cambridge University Press:
- 09 September 2022, pp. 3150-3192
- Print publication:
- September 2023
-
- Article
- Export citation
Simplicity of the Lyapunov spectrum for classes of Anosov flows
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 7 / July 2023
- Published online by Cambridge University Press:
- 02 May 2022, pp. 2437-2463
- Print publication:
- July 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A multiplicative ergodic theoretic characterization of relative equilibrium states
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 5 / May 2023
- Published online by Cambridge University Press:
- 24 March 2022, pp. 1455-1470
- Print publication:
- May 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Statistical stability and linear response for random hyperbolic dynamics
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 2 / February 2023
- Published online by Cambridge University Press:
- 07 December 2021, pp. 515-544
- Print publication:
- February 2023
-
- Article
- Export citation