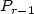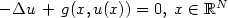Refine search
Actions for selected content:
4288 results in Numerical analysis and computational science
Regularity of the multi-configuration time-dependent Hartree approximation in quantum molecular dynamics
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 41 / Issue 2 / March 2007
- Published online by Cambridge University Press:
- 16 June 2007, pp. 315-331
- Print publication:
- March 2007
-
- Article
- Export citation
The time-dependent Born-Oppenheimer approximation
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 41 / Issue 2 / March 2007
- Published online by Cambridge University Press:
- 16 June 2007, pp. 297-314
- Print publication:
- March 2007
-
- Article
- Export citation
On the inf-sup condition for higher order mixed FEMon mesheswith hanging nodes
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 41 / Issue 1 / January 2007
- Published online by Cambridge University Press:
- 26 April 2007, pp. 1-20
- Print publication:
- January 2007
-
- Article
- Export citation
A continuous finite element method with face penaltyto approximate Friedrichs' systems
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 41 / Issue 1 / January 2007
- Published online by Cambridge University Press:
- 26 April 2007, pp. 55-76
- Print publication:
- January 2007
-
- Article
- Export citation
On the rate of convergence of a collocation projectionof the KdV equation
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 41 / Issue 1 / January 2007
- Published online by Cambridge University Press:
- 26 April 2007, pp. 95-110
- Print publication:
- January 2007
-
- Article
- Export citation
A multiscale correction method for local singular perturbations of the boundary
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 41 / Issue 1 / January 2007
- Published online by Cambridge University Press:
- 26 April 2007, pp. 111-127
- Print publication:
- January 2007
-
- Article
- Export citation
Convergence of the time-discretized monotonic schemes
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 41 / Issue 1 / January 2007
- Published online by Cambridge University Press:
- 26 April 2007, pp. 77-93
- Print publication:
- January 2007
-
- Article
- Export citation
Generalized combined field integral equationsfor the iterative solution of the three-dimensional Helmholtz equation
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 41 / Issue 1 / January 2007
- Published online by Cambridge University Press:
- 26 April 2007, pp. 147-167
- Print publication:
- January 2007
-
- Article
- Export citation
Locking free matching of different three dimensional models in structural mechanics
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 41 / Issue 1 / January 2007
- Published online by Cambridge University Press:
- 26 April 2007, pp. 129-145
- Print publication:
- January 2007
-
- Article
- Export citation
Godunov method for nonconservative hyperbolic systems
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 41 / Issue 1 / January 2007
- Published online by Cambridge University Press:
- 26 April 2007, pp. 169-185
- Print publication:
- January 2007
-
- Article
- Export citation
Schwarz domain decomposition preconditioners for discontinuous Galerkin approximationsof elliptic problems: non-overlapping case
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 41 / Issue 1 / January 2007
- Published online by Cambridge University Press:
- 26 April 2007, pp. 21-54
- Print publication:
- January 2007
-
- Article
- Export citation
Finite volume schemes for fully non-linear elliptic equationsin divergence form
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 40 / Issue 6 / November 2006
- Published online by Cambridge University Press:
- 15 February 2007, pp. 1069-1100
- Print publication:
- November 2006
-
- Article
- Export citation
Theoretical and numerical study of a quasi-linear Zakharov system describing Landau damping
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 40 / Issue 6 / November 2006
- Published online by Cambridge University Press:
- 15 February 2007, pp. 961-990
- Print publication:
- November 2006
-
- Article
- Export citation
Periodic solutions for nonlinear elliptic equations.Application to charged particle beam focusing systems
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 40 / Issue 6 / November 2006
- Published online by Cambridge University Press:
- 15 February 2007, pp. 1023-1052
- Print publication:
- November 2006
-
- Article
- Export citation
A second-order finite volume element methodon quadrilateralmeshes for elliptic equations
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 40 / Issue 6 / November 2006
- Published online by Cambridge University Press:
- 15 February 2007, pp. 1053-1067
- Print publication:
- November 2006
-
- Article
- Export citation
Robust a posteriori error estimates for finite element discretizations of the heat equation with discontinuous coefficients
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 40 / Issue 6 / November 2006
- Published online by Cambridge University Press:
- 15 February 2007, pp. 991-1021
- Print publication:
- November 2006
-
- Article
- Export citation
Numerical simulation of a pulsatile flow through a flexible channel
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 40 / Issue 6 / November 2006
- Published online by Cambridge University Press:
- 15 February 2007, pp. 1101-1125
- Print publication:
- November 2006
-
- Article
- Export citation
4 - Famous disasters
-
- Book:
- Writing Scientific Software
- Published online:
- 28 January 2010
- Print publication:
- 07 September 2006, pp 36-38
-
- Chapter
- Export citation
Part I - Numerical Software
-
- Book:
- Writing Scientific Software
- Published online:
- 28 January 2010
- Print publication:
- 07 September 2006, pp 1-2
-
- Chapter
- Export citation
Part IV - Tools
-
- Book:
- Writing Scientific Software
- Published online:
- 28 January 2010
- Print publication:
- 07 September 2006, pp 217-218
-
- Chapter
- Export citation