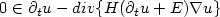Refine search
Actions for selected content:
4288 results in Numerical analysis and computational science
Index
-
- Book:
- Dynamic Data Assimilation
- Published online:
- 18 December 2009
- Print publication:
- 03 August 2006, pp 648-654
-
- Chapter
- Export citation
15 - Maximum likelihood method
- from PART IV - STATISTICAL ESTIMATION
-
- Book:
- Dynamic Data Assimilation
- Published online:
- 18 December 2009
- Print publication:
- 03 August 2006, pp 254-260
-
- Chapter
- Export citation
28 - Linear filtering: part II
- from PART VII - DATA ASSIMILATION: STOCHASTIC/DYNAMIC MODELS
-
- Book:
- Dynamic Data Assimilation
- Published online:
- 18 December 2009
- Print publication:
- 03 August 2006, pp 485-508
-
- Chapter
- Export citation
Acknowledgements
-
- Book:
- Dynamic Data Assimilation
- Published online:
- 18 December 2009
- Print publication:
- 03 August 2006, pp xxi-xxii
-
- Chapter
- Export citation
Epilogue
-
- Book:
- Dynamic Data Assimilation
- Published online:
- 18 December 2009
- Print publication:
- 03 August 2006, pp 628-629
-
- Chapter
- Export citation
5 - Linear least squares estimation: method of normal equations
- from PART II - DATA ASSIMILATION: DETERMINISTIC/STATIC MODELS
-
- Book:
- Dynamic Data Assimilation
- Published online:
- 18 December 2009
- Print publication:
- 03 August 2006, pp 99-120
-
- Chapter
- Export citation
Finite element analysis of a simplified stochastic Hookean dumbbells model arising from viscoelastic flows
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 40 / Issue 4 / July 2006
- Published online by Cambridge University Press:
- 15 November 2006, pp. 785-814
- Print publication:
- July 2006
-
- Article
- Export citation
New unilateral problems in stratigraphy
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 40 / Issue 4 / July 2006
- Published online by Cambridge University Press:
- 15 November 2006, pp. 765-784
- Print publication:
- July 2006
-
- Article
- Export citation
Study of a three component Cahn-Hilliard flow model
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 40 / Issue 4 / July 2006
- Published online by Cambridge University Press:
- 15 November 2006, pp. 653-687
- Print publication:
- July 2006
-
- Article
- Export citation
Diffusion and propagation problems in some ramified domains with a fractal boundary
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 40 / Issue 4 / July 2006
- Published online by Cambridge University Press:
- 15 November 2006, pp. 623-652
- Print publication:
- July 2006
-
- Article
- Export citation
Vibrations of a beam between obstacles. Convergence of a fully discretized approximation
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 40 / Issue 4 / July 2006
- Published online by Cambridge University Press:
- 15 November 2006, pp. 705-734
- Print publication:
- July 2006
-
- Article
- Export citation
The approximate Riemann solver of Roe appliedto a drift-flux two-phase flow model
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 40 / Issue 4 / July 2006
- Published online by Cambridge University Press:
- 15 November 2006, pp. 735-764
- Print publication:
- July 2006
-
- Article
- Export citation
A new domain decomposition method for the compressible Euler equations
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 40 / Issue 4 / July 2006
- Published online by Cambridge University Press:
- 15 November 2006, pp. 689-703
- Print publication:
- July 2006
-
- Article
- Export citation
3 - Sparse Grids for Higher Dimensional Problems
-
-
- Book:
- Foundations of Computational Mathematics, Santander 2005
- Published online:
- 13 May 2010
- Print publication:
- 29 June 2006, pp 106-161
-
- Chapter
- Export citation
6 - Eigenvalues and Nonsmooth Optimization
-
-
- Book:
- Foundations of Computational Mathematics, Santander 2005
- Published online:
- 13 May 2010
- Print publication:
- 29 June 2006, pp 208-229
-
- Chapter
- Export citation
5 - Dispersive Properties of Numerical Schemes for NSE
-
-
- Book:
- Foundations of Computational Mathematics, Santander 2005
- Published online:
- 13 May 2010
- Print publication:
- 29 June 2006, pp 181-207
-
- Chapter
- Export citation
Frontmatter
-
- Book:
- Foundations of Computational Mathematics, Santander 2005
- Published online:
- 13 May 2010
- Print publication:
- 29 June 2006, pp i-iv
-
- Chapter
- Export citation
10 - High-dimensional Transport-dominated Diffusion Problems
-
-
- Book:
- Foundations of Computational Mathematics, Santander 2005
- Published online:
- 13 May 2010
- Print publication:
- 29 June 2006, pp 343-370
-
- Chapter
- Export citation
9 - Smoothed Analysis of Algorithms and Heuristics
-
-
- Book:
- Foundations of Computational Mathematics, Santander 2005
- Published online:
- 13 May 2010
- Print publication:
- 29 June 2006, pp 274-342
-
- Chapter
- Export citation
Preface
-
- Book:
- Foundations of Computational Mathematics, Santander 2005
- Published online:
- 13 May 2010
- Print publication:
- 29 June 2006, pp vii-viii
-
- Chapter
- Export citation