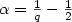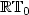Refine search
Actions for selected content:
4288 results in Numerical analysis and computational science
Relaxation models of phase transition flows
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 40 / Issue 2 / March 2006
- Published online by Cambridge University Press:
- 21 June 2006, pp. 331-352
- Print publication:
- March 2006
-
- Article
- Export citation
Numerical evidence of nonuniqueness in the evolutionof vortex sheets
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 40 / Issue 2 / March 2006
- Published online by Cambridge University Press:
- 21 June 2006, pp. 225-237
- Print publication:
- March 2006
-
- Article
- Export citation
Equivalence between lowest-order mixed finite elementand multi-pointfinite volume methods on simplicial meshes
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 40 / Issue 2 / March 2006
- Published online by Cambridge University Press:
- 21 June 2006, pp. 367-391
- Print publication:
- March 2006
-
- Article
- Export citation
Dynamic frictional contact of a viscoelastic beam
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 40 / Issue 2 / March 2006
- Published online by Cambridge University Press:
- 21 June 2006, pp. 295-310
- Print publication:
- March 2006
-
- Article
- Export citation
On the accuracy of Reissner–Mindlinplate modelfor stress boundary conditions
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 40 / Issue 2 / March 2006
- Published online by Cambridge University Press:
- 21 June 2006, pp. 269-294
- Print publication:
- March 2006
-
- Article
- Export citation
A viscosity solution method for Shape-From-Shadingwithout image boundary data
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 40 / Issue 2 / March 2006
- Published online by Cambridge University Press:
- 21 June 2006, pp. 393-412
- Print publication:
- March 2006
-
- Article
- Export citation
Numerical analysis of the quasistatic thermoviscoelastic thermistor problem
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 40 / Issue 2 / March 2006
- Published online by Cambridge University Press:
- 21 June 2006, pp. 353-366
- Print publication:
- March 2006
-
- Article
- Export citation
Discrete compactness for a discontinuous Galerkin approximation of Maxwell's system
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 40 / Issue 2 / March 2006
- Published online by Cambridge University Press:
- 21 June 2006, pp. 413-430
- Print publication:
- March 2006
-
- Article
- Export citation
An equilibrated residual method with a computableerror approximation for a singularly perturbed reaction-diffusion problem on anisotropicfinite element meshes
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 40 / Issue 2 / March 2006
- Published online by Cambridge University Press:
- 21 June 2006, pp. 239-267
- Print publication:
- March 2006
-
- Article
- Export citation
Finite volume methods for the valuationof American options
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 40 / Issue 2 / March 2006
- Published online by Cambridge University Press:
- 21 June 2006, pp. 311-330
- Print publication:
- March 2006
-
- Article
- Export citation
A numerical study on Neumann-Neumann methodsfor hp approximations on geometricallyrefined boundary layer meshes II. Three-dimensional problems
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 40 / Issue 1 / January 2006
- Published online by Cambridge University Press:
- 23 February 2006, pp. 99-122
- Print publication:
- January 2006
-
- Article
- Export citation
New mixed finite volume methods for second ordereliptic problems
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 40 / Issue 1 / January 2006
- Published online by Cambridge University Press:
- 23 February 2006, pp. 123-147
- Print publication:
- January 2006
-
- Article
- Export citation
Best N-term approximation in electronic structure calculations I.One-electron reduced density matrix
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 40 / Issue 1 / January 2006
- Published online by Cambridge University Press:
- 23 February 2006, pp. 49-61
- Print publication:
- January 2006
-
- Article
- Export citation
Convergence of a fully discrete finite element methodfor a degenerate parabolic system modelling nematic liquid crystals withvariable degree of orientation
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 40 / Issue 1 / January 2006
- Published online by Cambridge University Press:
- 23 February 2006, pp. 175-199
- Print publication:
- January 2006
-
- Article
- Export citation
Asymptotic analysis of an approximate model for time harmonic waves in media with thin slots
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 40 / Issue 1 / January 2006
- Published online by Cambridge University Press:
- 23 February 2006, pp. 63-97
- Print publication:
- January 2006
-
- Article
- Export citation
A viscoelastic model with non-local damping application to the human lungs
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 40 / Issue 1 / January 2006
- Published online by Cambridge University Press:
- 23 February 2006, pp. 201-224
- Print publication:
- January 2006
-
- Article
- Export citation
Convergence rates of symplectic Pontryaginapproximations in optimal control theory
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 40 / Issue 1 / January 2006
- Published online by Cambridge University Press:
- 23 February 2006, pp. 149-173
- Print publication:
- January 2006
-
- Article
- Export citation
Evaluation of the condition number in linear systems arising in finiteelement approximations
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 40 / Issue 1 / January 2006
- Published online by Cambridge University Press:
- 23 February 2006, pp. 29-48
- Print publication:
- January 2006
-
- Article
- Export citation
Analysis of a new augmented mixed finite element methodfor linear elasticity allowing $\mathbb{RT}_0$
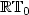 - $\mathbb{P}_1$
- $\mathbb{P}_1$ 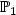 - $\mathbb{P}_0$
- $\mathbb{P}_0$ 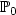 approximations
approximations
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 40 / Issue 1 / January 2006
- Published online by Cambridge University Press:
- 23 February 2006, pp. 1-28
- Print publication:
- January 2006
-
- Article
- Export citation
On nonoverlapping domain decomposition methodsfor the incompressible Navier-Stokes equations
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 39 / Issue 6 / November 2005
- Published online by Cambridge University Press:
- 15 November 2005, pp. 1251-1269
- Print publication:
- November 2005
-
- Article
- Export citation