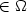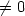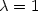Refine search
Actions for selected content:
4288 results in Numerical analysis and computational science
2 - Direct methods
-
- Book:
- Matrix Preconditioning Techniques and Applications
- Published online:
- 06 January 2010
- Print publication:
- 14 July 2005, pp 66-109
-
- Chapter
- Export citation
8 - Sparse wavelet preconditioners [T5]: approximation of Ãn×n and Ãn×n−1
-
- Book:
- Matrix Preconditioning Techniques and Applications
- Published online:
- 06 January 2010
- Print publication:
- 14 July 2005, pp 310-339
-
- Chapter
- Export citation
Plate section
-
- Book:
- Matrix Preconditioning Techniques and Applications
- Published online:
- 06 January 2010
- Print publication:
- 14 July 2005, pp -
-
- Chapter
- Export citation
The numerical interface coupling of nonlinearhyperbolic systems of conservation laws: II. The case of systems
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 39 / Issue 4 / July 2005
- Published online by Cambridge University Press:
- 15 August 2005, pp. 649-692
- Print publication:
- July 2005
-
- Article
- Export citation
Iteratively solving a kind of signorinitransmission problem in a unbounded domain
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 39 / Issue 4 / July 2005
- Published online by Cambridge University Press:
- 15 August 2005, pp. 715-726
- Print publication:
- July 2005
-
- Article
- Export citation
Finite element approximation for degenerate parabolic equations. an application of nonlinear semigroup theory
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 39 / Issue 4 / July 2005
- Published online by Cambridge University Press:
- 15 August 2005, pp. 755-780
- Print publication:
- July 2005
-
- Article
- Export citation
Mixed discontinuous Galerkin approximationof the Maxwell operator: The indefinite case
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 39 / Issue 4 / July 2005
- Published online by Cambridge University Press:
- 15 August 2005, pp. 727-753
- Print publication:
- July 2005
-
- Article
- Export citation
Characterization of the limit load in the caseof an unbounded elastic convex
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 39 / Issue 4 / July 2005
- Published online by Cambridge University Press:
- 15 August 2005, pp. 637-648
- Print publication:
- July 2005
-
- Article
- Export citation
On the Schwarz algorithms for the Elliptic Exterior Boundary Value Problems
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 39 / Issue 4 / July 2005
- Published online by Cambridge University Press:
- 15 August 2005, pp. 693-714
- Print publication:
- July 2005
-
- Article
- Export citation
Moving mesh for the axisymmetric harmonic map flow
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 39 / Issue 4 / July 2005
- Published online by Cambridge University Press:
- 15 August 2005, pp. 781-796
- Print publication:
- July 2005
-
- Article
- Export citation
Generalized Newton methods for the 2D-Signorini contact problem with friction in function space
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 39 / Issue 4 / July 2005
- Published online by Cambridge University Press:
- 15 August 2005, pp. 827-854
- Print publication:
- July 2005
-
- Article
- Export citation
Analysis of a prototypicalmultiscale method coupling atomistic and continuum mechanics
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 39 / Issue 4 / July 2005
- Published online by Cambridge University Press:
- 15 August 2005, pp. 797-826
- Print publication:
- July 2005
-
- Article
- Export citation
The mathematical theory of low Mach number flows
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 39 / Issue 3 / May 2005
- Published online by Cambridge University Press:
- 15 June 2005, pp. 441-458
- Print publication:
- May 2005
-
- Article
- Export citation
An example of low Mach (Froude) number effectsfor compressible flowswith nonconstant density(height) limit
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 39 / Issue 3 / May 2005
- Published online by Cambridge University Press:
- 15 June 2005, pp. 477-486
- Print publication:
- May 2005
-
- Article
- Export citation
Modelling of Natural Convection Flowswith Large Temperature Differences: A Benchmark Problem for LowMach Number Solvers. Part 2. Contributions to the June 2004conference
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 39 / Issue 3 / May 2005
- Published online by Cambridge University Press:
- 15 June 2005, pp. 617-621
- Print publication:
- May 2005
-
- Article
- Export citation
Numerical simulations of wave breaking
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 39 / Issue 3 / May 2005
- Published online by Cambridge University Press:
- 15 June 2005, pp. 591-607
- Print publication:
- May 2005
-
- Article
- Export citation
Local preconditioners for steady and unsteady flow applications
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 39 / Issue 3 / May 2005
- Published online by Cambridge University Press:
- 15 June 2005, pp. 515-535
- Print publication:
- May 2005
-
- Article
- Export citation
Multiple spatial scales in engineering and atmospheric low Mach number flows
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 39 / Issue 3 / May 2005
- Published online by Cambridge University Press:
- 15 June 2005, pp. 537-559
- Print publication:
- May 2005
-
- Article
- Export citation
On a diphasic low mach number system
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 39 / Issue 3 / May 2005
- Published online by Cambridge University Press:
- 15 June 2005, pp. 487-514
- Print publication:
- May 2005
-
- Article
- Export citation
Calculation of low Mach number acoustics: a comparisonof MPV, EIF and linearized Euler equations
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 39 / Issue 3 / May 2005
- Published online by Cambridge University Press:
- 15 June 2005, pp. 561-576
- Print publication:
- May 2005
-
- Article
- Export citation