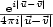Refine search
Actions for selected content:
4288 results in Numerical analysis and computational science
4 - Geometric integrators
-
- Book:
- Simulating Hamiltonian Dynamics
- Published online:
- 04 December 2009
- Print publication:
- 14 February 2005, pp 70-104
-
- Chapter
- Export citation
6 - Higher-order methods
-
- Book:
- Simulating Hamiltonian Dynamics
- Published online:
- 04 December 2009
- Print publication:
- 14 February 2005, pp 142-168
-
- Chapter
- Export citation
References
-
- Book:
- Simulating Hamiltonian Dynamics
- Published online:
- 04 December 2009
- Print publication:
- 14 February 2005, pp 357-373
-
- Chapter
- Export citation
8 - Rigid body dynamics
-
- Book:
- Simulating Hamiltonian Dynamics
- Published online:
- 04 December 2009
- Print publication:
- 14 February 2005, pp 199-233
-
- Chapter
- Export citation
2 - Numerical methods
-
- Book:
- Simulating Hamiltonian Dynamics
- Published online:
- 04 December 2009
- Print publication:
- 14 February 2005, pp 11-35
-
- Chapter
- Export citation
3 - Hamiltonian mechanics
-
- Book:
- Simulating Hamiltonian Dynamics
- Published online:
- 04 December 2009
- Print publication:
- 14 February 2005, pp 36-69
-
- Chapter
- Export citation
Preface
-
- Book:
- Simulating Hamiltonian Dynamics
- Published online:
- 04 December 2009
- Print publication:
- 14 February 2005, pp ix-xv
-
- Chapter
- Export citation
Index
-
- Book:
- Simulating Hamiltonian Dynamics
- Published online:
- 04 December 2009
- Print publication:
- 14 February 2005, pp 374-379
-
- Chapter
- Export citation
Contents
-
- Book:
- Simulating Hamiltonian Dynamics
- Published online:
- 04 December 2009
- Print publication:
- 14 February 2005, pp v-viii
-
- Chapter
- Export citation
5 - The modified equations
-
- Book:
- Simulating Hamiltonian Dynamics
- Published online:
- 04 December 2009
- Print publication:
- 14 February 2005, pp 105-141
-
- Chapter
- Export citation
Solutions of a nonhyperbolic pair of balance laws
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 39 / Issue 1 / January 2005
- Published online by Cambridge University Press:
- 15 March 2005, pp. 37-58
- Print publication:
- January 2005
-
- Article
- Export citation
A posteriori error bounds for reduced-basis approximationsofparametrized parabolic partial differential equations
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 39 / Issue 1 / January 2005
- Published online by Cambridge University Press:
- 15 March 2005, pp. 157-181
- Print publication:
- January 2005
-
- Article
- Export citation
Proposition de préconditionneurs pseudo-différentielspour l'équation CFIEde l'électromagnétisme
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 39 / Issue 1 / January 2005
- Published online by Cambridge University Press:
- 15 March 2005, pp. 147-155
- Print publication:
- January 2005
-
- Article
- Export citation
Error estimates in the Fast Multipole Method for scattering problemsPart 2: Truncation of the Gegenbauer series
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 39 / Issue 1 / January 2005
- Published online by Cambridge University Press:
- 15 March 2005, pp. 183-221
- Print publication:
- January 2005
-
- Article
- Export citation
Existence and uniqueness for dynamical unilateral contact with Coulomb friction: a model problem
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 39 / Issue 1 / January 2005
- Published online by Cambridge University Press:
- 15 March 2005, pp. 59-77
- Print publication:
- January 2005
-
- Article
- Export citation
Inverted finite elements: a new methodfor solving elliptic problems in unbounded domains
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 39 / Issue 1 / January 2005
- Published online by Cambridge University Press:
- 15 March 2005, pp. 109-145
- Print publication:
- January 2005
-
- Article
- Export citation
Coupling Darcy and Stokes equationsfor porous media with cracks
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 39 / Issue 1 / January 2005
- Published online by Cambridge University Press:
- 15 March 2005, pp. 7-35
- Print publication:
- January 2005
-
- Article
- Export citation
Classical solutions for the equations modelling the motion ofa ball in a bidimensional incompressible perfect fluid
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 39 / Issue 1 / January 2005
- Published online by Cambridge University Press:
- 15 March 2005, pp. 79-108
- Print publication:
- January 2005
-
- Article
- Export citation
11 - Error estimates for radial basis function interpolation
-
- Book:
- Scattered Data Approximation
- Published online:
- 22 February 2010
- Print publication:
- 13 December 2004, pp 172-205
-
- Chapter
- Export citation
References
-
- Book:
- Scattered Data Approximation
- Published online:
- 22 February 2010
- Print publication:
- 13 December 2004, pp 323-333
-
- Chapter
- Export citation