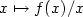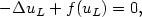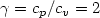Refine search
Actions for selected content:
4288 results in Numerical analysis and computational science
About the Authors
-
- Book:
- Proofs that Really Count
- Published by:
- Mathematical Association of America
- Published online:
- 05 July 2013
- Print publication:
- 01 January 2003, pp 194-194
-
- Chapter
- Export citation
2 - Gibonacci and Lucas Identities
-
- Book:
- Proofs that Really Count
- Published by:
- Mathematical Association of America
- Published online:
- 05 July 2013
- Print publication:
- 01 January 2003, pp 17-34
-
- Chapter
- Export citation
8 - Number Theory
-
- Book:
- Proofs that Really Count
- Published by:
- Mathematical Association of America
- Published online:
- 05 July 2013
- Print publication:
- 01 January 2003, pp 109-124
-
- Chapter
- Export citation
4 - Continued Fractions
-
- Book:
- Proofs that Really Count
- Published by:
- Mathematical Association of America
- Published online:
- 05 July 2013
- Print publication:
- 01 January 2003, pp 49-62
-
- Chapter
- Export citation
Approximation ofa semilinear elliptic problemin an unbounded domain
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 37 / Issue 1 / January 2003
- Published online by Cambridge University Press:
- 15 March 2003, pp. 117-132
- Print publication:
- January 2003
-
- Article
- Export citation
7 - Harmonic and Stirling Number Identities
-
- Book:
- Proofs that Really Count
- Published by:
- Mathematical Association of America
- Published online:
- 05 July 2013
- Print publication:
- 01 January 2003, pp 91-108
-
- Chapter
- Export citation
Numerical Study of Two Sparse AMG-methods
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 37 / Issue 1 / January 2003
- Published online by Cambridge University Press:
- 15 March 2003, pp. 133-142
- Print publication:
- January 2003
-
- Article
- Export citation
6 - Alternating Sign Binomial Identities
-
- Book:
- Proofs that Really Count
- Published by:
- Mathematical Association of America
- Published online:
- 05 July 2013
- Print publication:
- 01 January 2003, pp 81-90
-
- Chapter
- Export citation
Green's function pointwise estimates for the modified Lax–Friedrichs scheme
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 37 / Issue 1 / January 2003
- Published online by Cambridge University Press:
- 15 March 2003, pp. 1-39
- Print publication:
- January 2003
-
- Article
- Export citation
1 - Fibonacci Identities
-
- Book:
- Proofs that Really Count
- Published by:
- Mathematical Association of America
- Published online:
- 05 July 2013
- Print publication:
- 01 January 2003, pp 1-16
-
- Chapter
- Export citation
A general representation formula for boundary voltage perturbationscaused by internal conductivity inhomogeneities of low volume fraction
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 37 / Issue 1 / January 2003
- Published online by Cambridge University Press:
- 15 March 2003, pp. 159-173
- Print publication:
- January 2003
-
- Article
- Export citation
9 - Advanced Fibonacci & Lucas Identities
-
- Book:
- Proofs that Really Count
- Published by:
- Mathematical Association of America
- Published online:
- 05 July 2013
- Print publication:
- 01 January 2003, pp 125-146
-
- Chapter
- Export citation
Some Hints and Solutions for Chapter Exercises
-
- Book:
- Proofs that Really Count
- Published by:
- Mathematical Association of America
- Published online:
- 05 July 2013
- Print publication:
- 01 January 2003, pp 147-170
-
- Chapter
- Export citation
Dedication
-
- Book:
- Proofs that Really Count
- Published by:
- Mathematical Association of America
- Published online:
- 05 July 2013
- Print publication:
- 01 January 2003, pp vii-viii
-
- Chapter
- Export citation
Spectral methods for one-dimensional kinetic modelsofgranular flows and numerical quasi elastic limit
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 37 / Issue 1 / January 2003
- Published online by Cambridge University Press:
- 15 March 2003, pp. 73-90
- Print publication:
- January 2003
-
- Article
- Export citation
A Comparison of Dual Lagrange Multiplier Spaces for Mortar Finite Element Discretizations
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 36 / Issue 6 / November 2002
- Published online by Cambridge University Press:
- 15 January 2003, pp. 995-1012
- Print publication:
- November 2002
-
- Article
- Export citation
Enrichissement des interpolations d'éléments finisen utilisant des méthodes sans maillage
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 36 / Issue 6 / November 2002
- Published online by Cambridge University Press:
- 15 January 2003, pp. 1027-1042
- Print publication:
- November 2002
-
- Article
- Export citation
Convergence of the Schrödinger-Poisson system to the Euler equations under the influence of a large magnetic field
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 36 / Issue 6 / November 2002
- Published online by Cambridge University Press:
- 15 January 2003, pp. 1071-1090
- Print publication:
- November 2002
-
- Article
- Export citation
A hybrid scheme to compute contact discontinuitiesinone-dimensional Euler systems
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 36 / Issue 6 / November 2002
- Published online by Cambridge University Press:
- 15 January 2003, pp. 1133-1159
- Print publication:
- November 2002
-
- Article
- Export citation
On the two-dimensional compressible isentropic Navier–Stokes equations
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 36 / Issue 6 / November 2002
- Published online by Cambridge University Press:
- 15 January 2003, pp. 1091-1109
- Print publication:
- November 2002
-
- Article
- Export citation