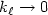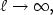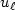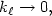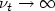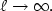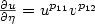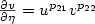Refine search
Actions for selected content:
4288 results in Numerical analysis and computational science
Numerical precision for differential inclusionswith uniqueness
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 36 / Issue 3 / May 2002
- Published online by Cambridge University Press:
- 15 August 2002, pp. 427-460
- Print publication:
- May 2002
-
- Article
- Export citation
A posteriori Error Estimates with Post-Processingfor Nonconforming Finite Elements
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 36 / Issue 3 / May 2002
- Published online by Cambridge University Press:
- 15 August 2002, pp. 489-503
- Print publication:
- May 2002
-
- Article
- Export citation
Motion with friction of a heavy particle on a manifold -applications to optimization
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 36 / Issue 3 / May 2002
- Published online by Cambridge University Press:
- 15 August 2002, pp. 505-516
- Print publication:
- May 2002
-
- Article
- Export citation
Edge finite elements for the approximation of Maxwell resolventoperator
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 36 / Issue 2 / March 2002
- Published online by Cambridge University Press:
- 15 May 2002, pp. 293-305
- Print publication:
- March 2002
-
- Article
- Export citation
New Wall Laws for the Unsteady Incompressible Navier-Stokes Equations on Rough Domains
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 36 / Issue 2 / March 2002
- Published online by Cambridge University Press:
- 15 May 2002, pp. 177-203
- Print publication:
- March 2002
-
- Article
- Export citation
An Optimum Design Problem in Magnetostatics
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 36 / Issue 2 / March 2002
- Published online by Cambridge University Press:
- 15 May 2002, pp. 223-239
- Print publication:
- March 2002
-
- Article
- Export citation
Numerical simulation of a point-source initiated flame ball with heat losses
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 36 / Issue 2 / March 2002
- Published online by Cambridge University Press:
- 15 May 2002, pp. 273-291
- Print publication:
- March 2002
-
- Article
- Export citation
Impact of the variations of the mixing length in a first order turbulentclosure system
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 36 / Issue 2 / March 2002
- Published online by Cambridge University Press:
- 15 May 2002, pp. 345-372
- Print publication:
- March 2002
-
- Article
- Export citation
Mixed Methods for the Approximation of Liquid Crystal Flows
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 36 / Issue 2 / March 2002
- Published online by Cambridge University Press:
- 15 May 2002, pp. 205-222
- Print publication:
- March 2002
-
- Article
- Export citation
Spectral Reconstruction of Piecewise Smooth Functions from Their Discrete Data
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 36 / Issue 2 / March 2002
- Published online by Cambridge University Press:
- 15 May 2002, pp. 155-175
- Print publication:
- March 2002
-
- Article
- Export citation
A posteriori error estimates for linear exterior problemsvia mixed-FEM and DtN mappings
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 36 / Issue 2 / March 2002
- Published online by Cambridge University Press:
- 15 May 2002, pp. 241-272
- Print publication:
- March 2002
-
- Article
- Export citation
Mathematical analysis and numerical simulationof a Reynolds-Koiter model for the elastohydrodynamic journal-bearing device
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 36 / Issue 2 / March 2002
- Published online by Cambridge University Press:
- 15 May 2002, pp. 325-343
- Print publication:
- March 2002
-
- Article
- Export citation
Finite Volume Methods for Elliptic PDE's: A NewApproach
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 36 / Issue 2 / March 2002
- Published online by Cambridge University Press:
- 15 May 2002, pp. 307-324
- Print publication:
- March 2002
-
- Article
- Export citation
Coupling of transport and diffusion models in linear transport theory
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 36 / Issue 1 / January 2002
- Published online by Cambridge University Press:
- 15 April 2002, pp. 69-86
- Print publication:
- January 2002
-
- Article
- Export citation
On the convergence rate of approximation schemes forHamilton-Jacobi-Bellman Equations
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 36 / Issue 1 / January 2002
- Published online by Cambridge University Press:
- 15 April 2002, pp. 33-54
- Print publication:
- January 2002
-
- Article
- Export citation
Isoparametric mixed finite element approximation of eigenvalues and eigenvectors of 4th order eigenvalue problems with variable coefficients
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 36 / Issue 1 / January 2002
- Published online by Cambridge University Press:
- 15 April 2002, pp. 1-32
- Print publication:
- January 2002
-
- Article
- Export citation
On the analysis of Bérenger's Perfectly Matched Layers for Maxwell's equations
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 36 / Issue 1 / January 2002
- Published online by Cambridge University Press:
- 15 April 2002, pp. 87-119
- Print publication:
- January 2002
-
- Article
- Export citation
Simultaneous vs. non-simultaneous blow-up in numerical approximations of aparabolic system with non-linear boundary conditions
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 36 / Issue 1 / January 2002
- Published online by Cambridge University Press:
- 15 April 2002, pp. 55-68
- Print publication:
- January 2002
-
- Article
- Export citation
A modal synthesis method for the elastoacoustic vibrationproblem
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 36 / Issue 1 / January 2002
- Published online by Cambridge University Press:
- 15 April 2002, pp. 121-142
- Print publication:
- January 2002
-
- Article
- Export citation
Numerical analysis of nonlinear elliptic-parabolic equations
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 36 / Issue 1 / January 2002
- Published online by Cambridge University Press:
- 15 April 2002, pp. 143-153
- Print publication:
- January 2002
-
- Article
- Export citation