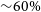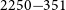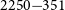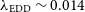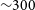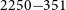Refine search
Actions for selected content:
28109 results in Astrophysics
7 - KS-Regularization
-
- Book:
- Gravitational Few-Body Dynamics
- Published online:
- 06 April 2020
- Print publication:
- 16 April 2020, pp 143-172
-
- Chapter
- Export citation
Index
-
- Book:
- Gravitational Few-Body Dynamics
- Published online:
- 06 April 2020
- Print publication:
- 16 April 2020, pp 243-244
-
- Chapter
- Export citation
1 - The Problems
-
- Book:
- Gravitational Few-Body Dynamics
- Published online:
- 06 April 2020
- Print publication:
- 16 April 2020, pp 3-14
-
- Chapter
- Export citation
3 - Analytical Tools
-
- Book:
- Gravitational Few-Body Dynamics
- Published online:
- 06 April 2020
- Print publication:
- 16 April 2020, pp 35-42
-
- Chapter
- Export citation
Dedication
-
- Book:
- Gravitational Few-Body Dynamics
- Published online:
- 06 April 2020
- Print publication:
- 16 April 2020, pp v-vi
-
- Chapter
- Export citation
References
-
- Book:
- Gravitational Few-Body Dynamics
- Published online:
- 06 April 2020
- Print publication:
- 16 April 2020, pp 237-242
-
- Chapter
- Export citation
9 - Motion in the Field of a Black Hole
-
- Book:
- Gravitational Few-Body Dynamics
- Published online:
- 06 April 2020
- Print publication:
- 16 April 2020, pp 211-220
-
- Chapter
- Export citation
Frontmatter
-
- Book:
- Gravitational Few-Body Dynamics
- Published online:
- 06 April 2020
- Print publication:
- 16 April 2020, pp i-iv
-
- Chapter
- Export citation
10 - Artificial Satellite Orbits
-
- Book:
- Gravitational Few-Body Dynamics
- Published online:
- 06 April 2020
- Print publication:
- 16 April 2020, pp 221-236
-
- Chapter
- Export citation
Preface
-
- Book:
- Gravitational Few-Body Dynamics
- Published online:
- 06 April 2020
- Print publication:
- 16 April 2020, pp xi-xii
-
- Chapter
- Export citation
2 - Two-Body Motion
-
- Book:
- Gravitational Few-Body Dynamics
- Published online:
- 06 April 2020
- Print publication:
- 16 April 2020, pp 15-34
-
- Chapter
- Export citation
4 - Variation of Parameters
-
- Book:
- Gravitational Few-Body Dynamics
- Published online:
- 06 April 2020
- Print publication:
- 16 April 2020, pp 43-54
-
- Chapter
- Export citation
6 - Symplectic Integration
-
- Book:
- Gravitational Few-Body Dynamics
- Published online:
- 06 April 2020
- Print publication:
- 16 April 2020, pp 81-142
-
- Chapter
- Export citation
Introduction
-
- Book:
- Gravitational Few-Body Dynamics
- Published online:
- 06 April 2020
- Print publication:
- 16 April 2020, pp 1-2
-
- Chapter
- Export citation
An ultra-wide bandwidth (704 to 4 032 MHz) receiver for the Parkes radio telescope
-
- Journal:
- Publications of the Astronomical Society of Australia / Volume 37 / 2020
- Published online by Cambridge University Press:
- 08 April 2020, e012
-
- Article
-
- You have access
- HTML
- Export citation
High-cadence optical transient searches using drift scan imaging I: Proof of concept with a pre-prototype system
-
- Journal:
- Publications of the Astronomical Society of Australia / Volume 37 / 2020
- Published online by Cambridge University Press:
- 08 April 2020, e015
-
- Article
-
- You have access
- HTML
- Export citation
Particle acceleration and the origin of the very high energy emission around black holes and relativistic jets
-
- Journal:
- Proceedings of the International Astronomical Union / Volume 14 / Issue S342 / May 2018
- Published online by Cambridge University Press:
- 07 April 2020, pp. 13-18
- Print publication:
- May 2018
-
- Article
-
- You have access
- Export citation
Modelling the polarised emission from black holes on event horizon-scales
-
- Journal:
- Proceedings of the International Astronomical Union / Volume 14 / Issue S342 / May 2018
- Published online by Cambridge University Press:
- 07 April 2020, pp. 9-12
- Print publication:
- May 2018
-
- Article
-
- You have access
- Export citation

Gravitational Few-Body Dynamics
- A Numerical Approach
-
- Published online:
- 06 April 2020
- Print publication:
- 16 April 2020
PKS 2250–351: A giant radio galaxy in Abell 3936
- Part of
-
- Journal:
- Publications of the Astronomical Society of Australia / Volume 37 / 2020
- Published online by Cambridge University Press:
- 25 March 2020, e013
-
- Article
-
- You have access
- HTML
- Export citation