Refine search
Actions for selected content:
26255 results in Theoretical Physics and Mathematical Physics
PSP volume 35 issue 3 Cover and Front matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 35 / Issue 3 / July 1939
- Published online by Cambridge University Press:
- 24 October 2008, pp. f1-f2
- Print publication:
- July 1939
-
- Article
-
- You have access
- Export citation
PSP volume 35 issue 3 Cover and Back matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 35 / Issue 3 / July 1939
- Published online by Cambridge University Press:
- 24 October 2008, pp. b1-b2
- Print publication:
- July 1939
-
- Article
-
- You have access
- Export citation
An automatic curve follower for use with the differential analyser
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 35 / Issue 3 / July 1939
- Published online by Cambridge University Press:
- 24 October 2008, pp. 494-505
- Print publication:
- July 1939
-
- Article
- Export citation
A new notation for quantum mechanics
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 35 / Issue 3 / July 1939
- Published online by Cambridge University Press:
- 24 October 2008, pp. 416-418
- Print publication:
- July 1939
-
- Article
- Export citation
On the derivation of discontinuous functions
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 35 / Issue 3 / July 1939
- Published online by Cambridge University Press:
- 24 October 2008, pp. 373-381
- Print publication:
- July 1939
-
- Article
- Export citation
The minimum χ′2 approximation
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 35 / Issue 3 / July 1939
- Published online by Cambridge University Press:
- 24 October 2008, p. 520
- Print publication:
- July 1939
-
- Article
- Export citation
Zur Summabilitätstheorie der Fourierschen Doppelreihe
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 35 / Issue 3 / July 1939
- Published online by Cambridge University Press:
- 24 October 2008, pp. 343-350
- Print publication:
- July 1939
-
- Article
- Export citation
Quantum electrodynamics. II
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 35 / Issue 3 / July 1939
- Published online by Cambridge University Press:
- 24 October 2008, pp. 438-462
- Print publication:
- July 1939
-
- Article
- Export citation
A problem in conduction of heat
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 35 / Issue 3 / July 1939
- Published online by Cambridge University Press:
- 24 October 2008, pp. 394-404
- Print publication:
- July 1939
-
- Article
- Export citation
The effect of interstellar matter on climatic variation
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 35 / Issue 3 / July 1939
- Published online by Cambridge University Press:
- 24 October 2008, pp. 405-415
- Print publication:
- July 1939
-
- Article
- Export citation
Note on the calculation of the Peltier effect
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 35 / Issue 3 / July 1939
- Published online by Cambridge University Press:
- 24 October 2008, pp. 521-522
- Print publication:
- July 1939
-
- Article
- Export citation
The production of 8Li by bombardment of boron with neutrons
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 35 / Issue 2 / April 1939
- Published online by Cambridge University Press:
- 24 October 2008, pp. 304-308
- Print publication:
- April 1939
-
- Article
- Export citation
The γ-rays of ionium
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 35 / Issue 2 / April 1939
- Published online by Cambridge University Press:
- 24 October 2008, pp. 322-326
- Print publication:
- April 1939
-
- Article
- Export citation
On the stability of nuclei against β-emission
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 35 / Issue 2 / April 1939
- Published online by Cambridge University Press:
- 24 October 2008, pp. 242-255
- Print publication:
- April 1939
-
- Article
- Export citation
A peculiarity in the infra-red absorption spectrum of germane
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 35 / Issue 2 / April 1939
- Published online by Cambridge University Press:
- 24 October 2008, pp. 341-342
- Print publication:
- April 1939
-
- Article
- Export citation
The heating of iron ammonium alum by alternating magnetic fields at very low temperatures
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 35 / Issue 2 / April 1939
- Published online by Cambridge University Press:
- 24 October 2008, pp. 327-335
- Print publication:
- April 1939
-
- Article
- Export citation
Base conditions and covariant systems in an algebraic threefold
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 35 / Issue 2 / April 1939
- Published online by Cambridge University Press:
- 24 October 2008, pp. 166-179
- Print publication:
- April 1939
-
- Article
- Export citation
On the easier Waring problem for powers of primes. II
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 35 / Issue 2 / April 1939
- Published online by Cambridge University Press:
- 24 October 2008, pp. 149-165
- Print publication:
- April 1939
-
- Article
- Export citation
A note on the boundary layer equations
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 35 / Issue 2 / April 1939
- Published online by Cambridge University Press:
- 24 October 2008, pp. 338-340
- Print publication:
- April 1939
-
- Article
- Export citation
A new proof of the joint product moment distribution
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 35 / Issue 2 / April 1939
- Published online by Cambridge University Press:
- 24 October 2008, pp. 336-338
- Print publication:
- April 1939
-
- Article
- Export citation
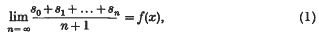

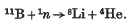
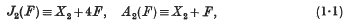
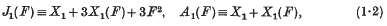
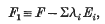
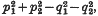 where the letters
where the letters