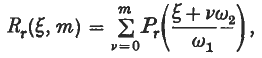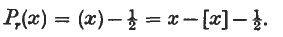Refine search
Actions for selected content:
26232 results in Theoretical Physics and Mathematical Physics
PSP volume 36 issue 1 Cover and Back matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 36 / Issue 1 / January 1940
- Published online by Cambridge University Press:
- 24 October 2008, p. b1
- Print publication:
- January 1940
-
- Article
-
- You have access
- Export citation
PSP volume 36 issue 1 Cover and Front matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 36 / Issue 1 / January 1940
- Published online by Cambridge University Press:
- 24 October 2008, p. f1
- Print publication:
- January 1940
-
- Article
-
- You have access
- Export citation
Properties of some superconductors
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 36 / Issue 1 / January 1940
- Published online by Cambridge University Press:
- 24 October 2008, pp. 84-93
- Print publication:
- January 1940
-
- Article
- Export citation
Notes on special systems of orthogonal Functions (III): A System of orthogonal polynomials†
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 36 / Issue 1 / January 1940
- Published online by Cambridge University Press:
- 24 October 2008, pp. 1-8
- Print publication:
- January 1940
-
- Article
- Export citation
The adsorption of dipoles
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 36 / Issue 1 / January 1940
- Published online by Cambridge University Press:
- 24 October 2008, pp. 69-78
- Print publication:
- January 1940
-
- Article
- Export citation
The inner shell ionization of atoms by electron impact
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 36 / Issue 1 / January 1940
- Published online by Cambridge University Press:
- 24 October 2008, pp. 43-52
- Print publication:
- January 1940
-
- Article
- Export citation
Paramagnetic hysteresis
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 36 / Issue 1 / January 1940
- Published online by Cambridge University Press:
- 24 October 2008, pp. 79-83
- Print publication:
- January 1940
-
- Article
- Export citation
The interpretation of ionization measurements in gases at high pressures
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 36 / Issue 1 / January 1940
- Published online by Cambridge University Press:
- 24 October 2008, pp. 101-126
- Print publication:
- January 1940
-
- Article
- Export citation
The approximate local monotony of measurable functions
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 36 / Issue 1 / January 1940
- Published online by Cambridge University Press:
- 24 October 2008, pp. 9-13
- Print publication:
- January 1940
-
- Article
- Export citation
Critical conditions in neutron multiplication
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 35 / Issue 4 / November 1939
- Published online by Cambridge University Press:
- 24 October 2008, pp. 610-615
- Print publication:
- November 1939
-
- Article
- Export citation
The evolution of the stars
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 35 / Issue 4 / November 1939
- Published online by Cambridge University Press:
- 24 October 2008, pp. 592-609
- Print publication:
- November 1939
-
- Article
- Export citation
Photoemission in Geiger-Müller counters
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 35 / Issue 4 / November 1939
- Published online by Cambridge University Press:
- 24 October 2008, pp. 654-657
- Print publication:
- November 1939
-
- Article
- Export citation
PSP volume 35 issue 4 Cover and Front matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 35 / Issue 4 / November 1939
- Published online by Cambridge University Press:
- 24 October 2008, pp. f1-f2
- Print publication:
- November 1939
-
- Article
-
- You have access
- Export citation
The exchange force between three heavy particles due to the meson exchange field
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 35 / Issue 4 / November 1939
- Published online by Cambridge University Press:
- 24 October 2008, pp. 616-621
- Print publication:
- November 1939
-
- Article
- Export citation
Introduction to the theory of operators. IV Linear functionals
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 35 / Issue 4 / November 1939
- Published online by Cambridge University Press:
- 24 October 2008, pp. 562-578
- Print publication:
- November 1939
-
- Article
- Export citation
Proceedings at the Meetings Held During the Session 1938–1939
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 35 / Issue 4 / November 1939
- Published online by Cambridge University Press:
- 24 October 2008, pp. 659-663
- Print publication:
- November 1939
-
- Article
- Export citation
An apparent inconsistency arising from tests of significance based on fiducial distributions of unknown parameters
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 35 / Issue 4 / November 1939
- Published online by Cambridge University Press:
- 24 October 2008, pp. 579-591
- Print publication:
- November 1939
-
- Article
- Export citation
A critical examination of the Benedicks homogeneous thermoelectric effect
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 35 / Issue 4 / November 1939
- Published online by Cambridge University Press:
- 24 October 2008, pp. 622-636
- Print publication:
- November 1939
-
- Article
- Export citation
On a Hardy-Littlewood problem of diophantine approximation
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 35 / Issue 4 / November 1939
- Published online by Cambridge University Press:
- 24 October 2008, pp. 527-547
- Print publication:
- November 1939
-
- Article
- Export citation
The Cambridge Philosophical Society Statement of Accounts for the Period 1 January 1938 to 31 July 1938
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 35 / Issue 4 / November 1939
- Published online by Cambridge University Press:
- 24 October 2008, pp. 664-665
- Print publication:
- November 1939
-
- Article
- Export citation
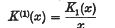
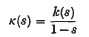
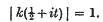
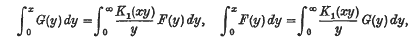
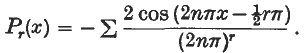 .
.