Article contents
An unusual stochastic order relation with some applications in sampling and epidemic theory
Published online by Cambridge University Press: 01 July 2016
Abstract
One expects, intuitively, that the total damage caused by an epidemic increases, in a certain sense, with the infection intensity exerted by the infectives during their lifelength. The original object of the present work is to make precise in which probabilistic terms such a statement does indeed hold true, when the spread of the disease is described by a collective Reed–Frost model and the global cost is represented by the final size and severity. Surprisingly, this problem leads us to introduce an order relation for 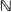 -valued random variables, unusual in the literature, based on the descending factorial moments. Further applications of the ordering occur when comparing certain sampling procedures through the number of un-sampled individuals. In particular, it is used to reinforce slightly comparison results obtained earlier for two such samplings.
-valued random variables, unusual in the literature, based on the descending factorial moments. Further applications of the ordering occur when comparing certain sampling procedures through the number of un-sampled individuals. In particular, it is used to reinforce slightly comparison results obtained earlier for two such samplings.
Keywords
MSC classification
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Applied Probability Trust 1993
References
- 9
- Cited by

