Hostname: page-component-76fb5796d-vfjqv Total loading time: 0 Render date: 2024-04-26T10:30:19.724Z Has data issue: false hasContentIssue false
  • English
  • Français

Degree distributions in recursive trees with fitnesses

Part of: Graph theory Operations research and management science Markov processes

Published online by Cambridge University Press:  06 March 2023

Tejas Iyer Open the ORCID record for Tejas Iyer [Opens in a new window]
Tejas Iyer*
Affiliation:
Weierstrass Institute, Berlin
*
*Postal address: Weierstrass Institute, Berlin, Germany. Email address: tejas.iyer@wias-berlin.de
Get access Rights & Permissions [Opens in a new window]

Abstract

We study a general model of recursive trees where vertices are equipped with independent weights and at each time-step a vertex is sampled with probability proportional to its fitness function, which is a function of its weight and degree, and connects to 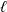$\ell$ new-coming vertices. Under a certain technical assumption, applying the theory of Crump–Mode–Jagers branching processes, we derive formulas for the limiting distributions of the proportion of vertices with a given degree and weight, and proportion of edges with endpoint having a certain weight. As an application of this theorem, we rigorously prove observations of Bianconi related to the evolving Cayley tree (Phys. Rev. E 66, paper no. 036116, 2002). We also study the process in depth when the technical condition can fail in the particular case when the fitness function is affine, a model we call ‘generalised preferential attachment with fitness’. We show that this model can exhibit condensation, where a positive proportion of edges accumulates around vertices with maximal weight, or, more drastically, can have a degenerate limiting degree distribution, where the entire proportion of edges accumulates around these vertices. Finally, we prove stochastic convergence for the degree distribution under a different assumption of a strong law of large numbers for the partition function associated with the process.

Keywords

Complex networksgeneralised preferential attachment with fitnessrandom recursive treeplane-oriented recursive treeCrump–Mode–Jagers branching processescondensation

MSC classification

Primary: 90B15: Network models, stochastic
Secondary: 60J20: Applications of Markov chains and discrete-time Markov processes on general state spaces (social mobility, learning theory, industrial processes, etc.) 05C80: Random graphs
Type
Original Article
Information
Advances in Applied Probability , Volume 55 , Issue 2 , June 2023 , pp. 407 - 443
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of Applied Probability Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Antunović, T., Mossel, E. and Rácz, M. Z. (2016). Coexistence in preferential attachment networks. Combinatorics Prob. Comput. 25, 797–822.CrossRefGoogle Scholar
Barabási, A.-L. and Albert, R. (1999). Emergence of scaling in random networks. Science 286, 509–512.CrossRefGoogle ScholarPubMed
Bhamidi, S. (2007). Universal techniques to analyze preferential attachment trees: global and local analysis. Preprint. Available at https://pdfs.semanticscholar.org/e7fb/8c999ff62a5f080e4c329a7a450f41fb1528.pdf.Google Scholar
Bianconi, G. (2002). Growing Cayley trees described by a Fermi distribution. Phys. Rev. E 66, paper no. 036116.CrossRefGoogle ScholarPubMed
Bianconi, G. and Barabási, A.-L. (2001). Bose–Einstein condensation in complex networks. Phys. Rev. Lett. 86, 5632–5635.CrossRefGoogle ScholarPubMed
Bollobás, B. and Riordan, O. (2004). Shortest paths and load scaling in scale-free trees. Phys. Rev. E 69, paper no. 036114.CrossRefGoogle ScholarPubMed
Bollobás, B., Riordan, O., Spencer, J. and Tusnády, G. (2001). The degree sequence of a scale-free random graph process. Random Structures Algorithms 18, 279–290.CrossRefGoogle Scholar
Borgs, C., Chayes, J., Daskalakis, C. and Roch, S. (2007). First to market is not everything: an analysis of preferential attachment with fitness. In STOC ’07—Proceedings of the 39th Annual ACM Symposium on Theory of Computing, Association for Computing Machinery, New York, pp. 135–144.CrossRefGoogle Scholar
Borovkov, K. A. and Vatutin, V. A. (2006). On the asymptotic behaviour of random recursive trees in random environments. Adv. Appl. Prob. 38, 1047–1070.CrossRefGoogle Scholar
Chen, W.-C. and Ni, W.-C. (1994). Internal path length of the binary representation of heap-ordered trees. Inf. Process. Lett. 51, 129–132.CrossRefGoogle Scholar
Dereich, S. (2016). Preferential attachment with fitness: unfolding the condensate. Electron. J. Prob. 21, paper no. 3, 38 pp.CrossRefGoogle Scholar
Dereich, S., Mailler, C. and Mörters, P. (2017). Nonextensive condensation in reinforced branching processes. Ann. Appl. Prob. 27, 2539–2568.CrossRefGoogle Scholar
Dereich, S. and Mörters, P. (2009). Random networks with sublinear preferential attachment: degree evolutions. Electron. J. Prob. 14, 1222–1267.CrossRefGoogle Scholar
Dereich, S. and Ortgiese, M. (2014). Robust analysis of preferential attachment models with fitness. Combinatorics Prob. Comput. 23, 386–411.CrossRefGoogle Scholar
Drmota, M. (2009). Random Trees: An Interplay between Combinatorics and Probability. Springer, Vienna.CrossRefGoogle Scholar
Ergün, G. and Rodgers, G. J. (2002). Growing random networks with fitness. Physica A 303, 261–272.CrossRefGoogle Scholar
Fountoulakis, N., Iyer, T., Mailler, C. and Sulzbach, H. (2019). Dynamical models for random simplicial complexes. Preprint. Available at https://arxiv.org/abs/1910.12715.Google Scholar
Garavaglia, A., van der Hofstad, R. and Woeginger, G. (2017). The dynamics of power laws: fitness and aging in preferential attachment trees. J. Statist. Phys. 168, 1137–1179.CrossRefGoogle Scholar
Hiesmayr, E. and Işlak, Ü. (2020). Asymptotic results on Hoppe trees and their variations. J. Appl. Prob. 57, 441–457.CrossRefGoogle Scholar
Holmgren, C. and Janson, S. (2017). Fringe trees, Crump–Mode–Jagers branching processes and m-ary search trees. Prob. Surveys 14, 53–154.CrossRefGoogle Scholar
Janson, S. (2021). A.s. convergence for infinite colour Pólya urns associated with random walks. Ark. Mat. 59, 87–123.CrossRefGoogle Scholar
Jordan, J. (2018). Preferential attachment graphs with co-existing types of different fitnesses. J. Appl. Prob. 55, 1211–1227.CrossRefGoogle Scholar
Lodewijks, B. and Ortgiese, M. (2020). A phase transition for preferential attachment models with additive fitness. Electron. J. Prob. 25, paper no. 146, 54 pp.Google Scholar
Mahmoud, H. M. (1992). Distances in random plane-oriented recursive trees. J. Comput. Appl. Math. 41, 237–245.CrossRefGoogle Scholar
Mahmoud, H. M. (1992). Evolution of Random Search Trees. John Wiley, New York.Google Scholar
Mahmoud, H. M., Smythe, R. T. and Szymański, J. (1993). On the structure of random plane-oriented recursive trees and their branches. Random Structures Algorithms 4, 151–176.CrossRefGoogle Scholar
Móri, T. F. (2002). On random trees. Studia Sci. Math. Hung. 39, 143–155.Google Scholar
Na, H. S. and Rapoport, A. (1970). Distribution of nodes of a tree by degree. Math. Biosci. 6, 313–329.CrossRefGoogle Scholar
Najock, D. and Heyde, C. C. (1982). On the number of terminal vertices in certain random trees with an application to stemma construction in philology. J. Appl. Prob. 19, 675–680.CrossRefGoogle Scholar
Nerman, O. (1981). On the convergence of supercritical general (C-M-J) branching processes. Z. Wahrscheinlichkeitsth. 57, 365–395.CrossRefGoogle Scholar
Oliveira, R. and Spencer, J. (2005). Connectivity transitions in networks with super-linear preferential attachment. Internet Math. 2, 121–163.CrossRefGoogle Scholar
Prodinger, H. and Urbanek, F. J. (1983). On monotone functions of tree structures. Discrete Appl. Math. 5, 223–239.CrossRefGoogle Scholar
Rudas, A., Tóth, B. and Valkó, B. (2007). Random trees and general branching processes. Random Structures Algorithms 31, 186–202.CrossRefGoogle Scholar
Sénizergues, D. (2021). Geometry of weighted recursive and affine preferential attachment trees. Electron. J. Prob. 26, paper no. 80, 56 pp.CrossRefGoogle Scholar
Szabó, G., Alava, M. and Kertész, J. (2002). Shortest paths and load scaling in scale-free trees. Phys. Rev. E 66, paper no. 026101.CrossRefGoogle ScholarPubMed
Szymański, J. (1987). On a nonuniform random recursive tree. In Random Graphs ’85 (Poznań, 1985), North-Holland, Amsterdam, pp. 297–306.Google Scholar
Van der Hofstad, R. (2016). Random Graphs and Complex Networks, Vol. 1. Cambridge University Press.CrossRefGoogle Scholar
Van der Hofstad, R. (2021). Random Graphs and Complex Networks, Vol. 2. Preprint. Available at https://www.win.tue.nl/rhofstad/NotesRGCNII.pdf.Google Scholar