Hostname: page-component-7dd5485656-wxk4p Total loading time: 0 Render date: 2025-10-29T12:43:29.619Z Has data issue: false hasContentIssue false
  • English
  • Français

A dual risk model with additive and proportional gains: ruin probability and dividends

Part of: Stochastic processes Markov processes Stochastic systems and control

Published online by Cambridge University Press:  08 February 2023

Onno Boxma ,
Esther Frostig  and
Zbigniew Palmowski Open the ORCID record for Zbigniew Palmowski [Opens in a new window]
Onno Boxma*
Affiliation:
Eindhoven University of Technology
Esther Frostig*
Affiliation:
University of Haifa
Zbigniew Palmowski*
Affiliation:
Wrocław University of Science and Technology
*
*Postal address: Department of Mathematics and Computer Science, Eindhoven University of Technology, P.O. Box 513, 5600 MB Eindhoven, the Netherlands. Email address: o.j.boxma@tue.nl
**Postal address: Department of Statistics, Haifa University, Haifa, Israel. Email address: frostig@stat.haifa.ac.il
***Postal address: Department of Applied Mathematics, Wrocław University of Science and Technology, Wrocław, Poland. Email address: zbigniew.palmowski@pwr.edu.pl
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider a dual risk model with constant expense rate and i.i.d. exponentially distributed gains 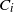$C_i$ (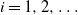$i=1,2,\dots$) that arrive according to a renewal process with general interarrival times. We add to this classical dual risk model the proportional gain feature; that is, if the surplus process just before the ith arrival is at level u, then for 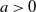$a>0$ the capital jumps up to the level 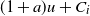$(1+a)u+C_i$. The ruin probability and the distribution of the time to ruin are determined. We furthermore identify the value of discounted cumulative dividend payments, for the case of a Poisson arrival process of proportional gains. In the dividend calculations, we also consider a random perturbation of our basic risk process modeled by an independent Brownian motion with drift.

Keywords

Dual risk modelruin probabilitytime to ruindividend

MSC classification

Primary: 60J99: None of the above, but in this section
Secondary: 93E20: Optimal stochastic control 60G51: Processes with independent increments; L'evy processes

Information

Type
Original Article
Information
Advances in Applied Probability , Volume 55 , Issue 2 , June 2023 , pp. 549 - 580
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of Applied Probability Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Afonso, L. B., Cardoso, R. M. R. and dos Reis, E. (2013). Dividend problems in the dual risk model. Insurance Math. Econom. 53, 906–918.CrossRefGoogle Scholar
Albrecher, H., Badescu, A. L. and Landriault, D. (2008). On the dual risk model with tax payments. Insurance Math. Econom. 42, 1086–1094.CrossRefGoogle Scholar
Avanzi, B. (2009). Strategies for dividend distribution: a review. N. Amer. Actuarial J. 13, 217–251.CrossRefGoogle Scholar
Avanzi, B. and Gerber, H. U. (2008). Optimal dividends in the dual risk model with diffusion. ASTIN Bull. 38, 653–667.CrossRefGoogle Scholar
Avanzi, B., Gerber, H. U. and Shiu, E. S. W. (2007). Optimal dividends in the dual model. Insurance Math. Econom. 41, 111–123.CrossRefGoogle Scholar
Avanzi, B., Pérez, J. L., Wong, B. and Yamazaki, K. (2017). On optimal joint reflective and refractive dividend strategies in spectrally positive Lévy models. Insurance Math. Econom. 72, 148–162.CrossRefGoogle Scholar
Avram, F., Palmowski, Z. and Pistorius, M. (2007). On the optimal dividend problem for a spectrally negative Lévy process. Ann. Appl. Prob. 17, 156–180.CrossRefGoogle Scholar
Bayraktar, E., Kyprianou, A. and Yamazaki, K. (2014). On the optimal dividends in the dual model. ASTIN Bull. 43, 359–372.CrossRefGoogle Scholar
Boxma, O. J. and Frostig, E. (2018). The dual risk model with dividends taken at arrival. Insurance Math. Econom. 83, 83–92.CrossRefGoogle Scholar
Boxma, O. J., Löpker, A. and Mandjes, M. R. H. (2020). On two classes of reflected autoregressive processes. J. Appl. Prob. 57, 657–678.CrossRefGoogle Scholar
Boxma, O. J., Löpker, A., Mandjes, M. R. H. and Palmowski, Z. (2021). A multiplicative version of the Lindley recursion. Queueing Systems 98, 225–245.CrossRefGoogle Scholar
Boxma, O. J., Mandjes, M. R. H. and Reed, J. (2016). On a class of reflected AR(1) processes. J. Appl. Prob. 53, 816–832.CrossRefGoogle Scholar
Buraczewski, D., Damek, E. and Mikosch, T. (2016). Stochastic Models with Power-Law Tails: The Equation $X = AX + B$ . Springer, Cham.CrossRefGoogle Scholar
Cohen, J. W. (1982). The Single Server Queue. North-Holland, Amsterdam.Google Scholar
Hale, J. K. and Verduyn Lunel, S. M. (1993). Introduction to Functional Differential Equations. Springer, Berlin.CrossRefGoogle Scholar
Kuznetsov, A., Kyprianou, A. E. and Rivero, V. (2013). The theory of scale functions for spectrally negative Lévy processes. In Lévy Matters II, Springer, Berlin, pp. 97–186.Google Scholar
Kyprianou, A. E. (2006). Introductory Lectures on Fluctuations of Lévy Processes with Applications. Springer, Berlin.Google Scholar
Marciniak, E. and Palmowski, Z. (2018). On the optimal dividend problem in the dual models with surplus-dependent premiums. J. Optimization Theory Appl. 179, 533–552.CrossRefGoogle Scholar
Ng, A. (2009). On the dual model with a dividend threshold. Insurance Math. Econom. 44, 315–324.CrossRefGoogle Scholar
Palmowski, Z., Ramsden, L. and Papaioannou, A. D. (2018). Parisian ruin for the dual risk process in discrete-time. Europ. Actuarial J. 8, 197–214.CrossRefGoogle ScholarPubMed
Prabhu, N. U. (1998). Stochastic Storage Processes. Springer, New York.CrossRefGoogle Scholar
Ross, S. (2009). Introduction to Probability Models, 10th edn. Academic Press, New York.Google Scholar
Vlasiou, M. (2006). Lindley-type recursions. Doctoral Thesis, Eindhoven University of Technology.Google Scholar
Yin, C. and Wen, Y. (2013). Optimal dividend problem with terminal value for spectrally positive Lévy processes. Insurance Math. Econom. 53, 769–773.CrossRefGoogle Scholar
Yin, C., Wen, Y. and Zhao, Y. (2014). On the dividend problem for a spectrally positive Lévy process. ASTIN Bull. 44, 635–651.CrossRefGoogle Scholar