Hostname: page-component-89b8bd64d-46n74 Total loading time: 0 Render date: 2026-05-08T08:55:16.936Z Has data issue: false hasContentIssue false
  • English
  • Français

Limit theorems for sequential MCMC methods

Part of: Stochastic processes Markov processes Limit theorems Parametric inference Probabilistic methods, simulation and stochastic differential equations

Published online by Cambridge University Press:  15 July 2020

Axel Finke ,
Arnaud Doucet  and
Adam M. Johansen
Axel Finke*
Affiliation:
National University of Singapore
Arnaud Doucet*
Affiliation:
University of Oxford
Adam M. Johansen*
Affiliation:
University of Warwick & The Alan Turing Institute
*
*Postal address: Department of Statistics & Applied Probability, Block S16, Level 7, 6 Science Drive 2, Faculty of Science, National University of Singapore, Singapore 117546. Email: axel.finke@nus.edu.sg
*Postal address: Department of Statistics & Applied Probability, Block S16, Level 7, 6 Science Drive 2, Faculty of Science, National University of Singapore, Singapore 117546. Email: axel.finke@nus.edu.sg
***Postal address: Department of Statistics, University of Warwick, Coventry, CV4 7AL, UK; The Alan Turing Institute, 96 Euston Rd, Kings Cross, London NW1 2DB, UK
Get access Rights & Permissions [Opens in a new window]

Abstract

Both sequential Monte Carlo (SMC) methods (a.k.a. ‘particle filters’) and sequential Markov chain Monte Carlo (sequential MCMC) methods constitute classes of algorithms which can be used to approximate expectations with respect to (a sequence of) probability distributions and their normalising constants. While SMC methods sample particles conditionally independently at each time step, sequential MCMC methods sample particles according to a Markov chain Monte Carlo (MCMC) kernel. Introduced over twenty years ago in [6], sequential MCMC methods have attracted renewed interest recently as they empirically outperform SMC methods in some applications. We establish an 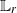$\mathbb{L}_r$-inequality (which implies a strong law of large numbers) and a central limit theorem for sequential MCMC methods and provide conditions under which errors can be controlled uniformly in time. In the context of state-space models, we also provide conditions under which sequential MCMC methods can indeed outperform standard SMC methods in terms of asymptotic variance of the corresponding Monte Carlo estimators.

Keywords

Sequential Monte Carlo methodsparticle filtersMarkov chain Monte Carlo methodsalmost sure convergencemultivariate central limit theoremtime-uniform convergence

MSC classification

Primary: 65C05: Monte Carlo methods 60F05: Central limit and other weak theorems 60F25: $L^p$-limit theorems 60G35: Signal detection and filtering
Secondary: 60J05: Discrete-time Markov processes on general state spaces 62F15: Bayesian inference 68U20: Simulation

Information

Type
Original Article
Information
Advances in Applied Probability , Volume 52 , Issue 2 , June 2020 , pp. 377 - 403
Copyright
© Applied Probability Trust 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Andrieu, C., Doucet, A. and Holenstein, R. (2010). Particle Markov chain Monte Carlo methods. J. R. Statist. Soc. B [Statist. Methodology] 72, 269–342. With discussion.CrossRefGoogle Scholar
Andrieu, C., Jasra, A., Doucet, A. and Del Moral, P. (2011). On nonlinear Markov chain Monte Carlo. Bernoulli 17, 987–1014.CrossRefGoogle Scholar
Andrieu, C. and Roberts, G. O. (2009). The pseudo-marginal approach for efficient Monte Carlo computations. Ann. Statist. 37, 697–725.CrossRefGoogle Scholar
Baxendale, P. H. (2005). Renewal theory and computable convergence rates for geometrically ergodic Markov chains. Ann. Appl. Prob. 15, 700–738.10.1214/105051604000000710CrossRefGoogle Scholar
Bercu, B., Del Moral, P. and Doucet, A. (2012). Fluctuations of interacting Markov chain Monte Carlo methods. Stoch. Proc. Appl. 122, 1304–1331.10.1016/j.spa.2012.01.001CrossRefGoogle Scholar
Berzuini, C., Best, N. G., Gilks, W. R. and Larizza, C. (1997). Dynamic conditional independence models and Markov chain Monte Carlo methods. J. Amer. Statist. Soc. 92, 1403–1412.10.1080/01621459.1997.10473661CrossRefGoogle Scholar
Brockwell, A., Del Moral, P. and Doucet, A. (2010). Sequentially interacting Markov chain Monte Carlo methods. Ann. Statist 38, 3387–3411.10.1214/09-AOS747CrossRefGoogle Scholar
Carmi, A., Septier, F. and Godsill, S. J. (2012). The Gaussian mixture MCMC particle algorithm for dynamic cluster tracking. Automatica 48, 2454–2467.10.1016/j.automatica.2012.06.086CrossRefGoogle Scholar
Chopin, N. (2004). Central limit theorem for sequential Monte Carlo methods and its application to Bayesian inference. Ann. Statist. 32, 2385–2411.CrossRefGoogle Scholar
Del Moral, P. (2004). Feynman-Kac Formulae: Genealogical and Interacting Particle Systems with Applications. Springer, New York.10.1007/978-1-4684-9393-1CrossRefGoogle Scholar
Del Moral, P. and Doucet, A. (2010). Interacting Markov chain Monte Carlo methods for solving nonlinear measure-valued equations. Ann. Appl. Prob. 20, 593–639.10.1214/09-AAP628CrossRefGoogle Scholar
Douc, R., Moulines, E. and Olsson, J. (2014). Long-term stability of sequential Monte Carlo methods under verifiable conditions. Ann. Appl. Prob. 24, 1767–1802.10.1214/13-AAP962CrossRefGoogle Scholar
Doucet, A., Pitt, M., Deligiannidis, G. and Kohn, R. (2015). Efficient implementation of Markov chain Monte Carlo when using an unbiased likelihood estimator. Biometrika 102, 295–313.10.1093/biomet/asu075CrossRefGoogle Scholar
Finke, A., Doucet, A. and Johansen, A. M. (2016). On embedded hidden Markov models and particle Markov chain Monte Carlo methods. Preprint. Available at http://arxiv.org/abs/1610.08962.Google Scholar
Golightly, A. and Wilkinson, D. J. (2006). Bayesian sequential inference for nonlinear multivariate diffusions. Statist. Comput. 16, 323–338.10.1007/s11222-006-9392-xCrossRefGoogle Scholar
Gordon, N. J., Salmond, D. J. and Smith, A. F. M. (1993). Novel approach to nonlinear/non-Gaussian Bayesian state estimation. IEE Proc. F, Radar and Signal Processing 140, 107–113.10.1049/ip-f-2.1993.0015CrossRefGoogle Scholar
Johansen, A. M. and Doucet, A. (2007). Auxiliary variable sequential Monte Carlo methods. Technical report 07:09. University of Bristol, Statistics Groups.Google Scholar
Johansen, A. M. and Doucet, A. (2008). A note on auxiliary particle filters. Statist. Prob. Lett. 78, 1498–1504.10.1016/j.spl.2008.01.032CrossRefGoogle Scholar
Kallenberg, O. (2006). Foundations of Modern Probability. Springer, New York.Google Scholar
Künsch, H. R. (2005). Recursive Monte Carlo filters: algorithms and theoretical analysis. Ann. Statist. 33, 1983–2021.10.1214/009053605000000426CrossRefGoogle Scholar
Künsch, H. R. (2013). Particle filters. Bernoulli 19, 1391–1403.10.3150/12-BEJSP07CrossRefGoogle Scholar
Li, Y. and Coates, M. (2017). Sequential MCMC with invertible particle flow. In 2017 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), IEEE, pp. 3844–3848.CrossRefGoogle Scholar
Lin, M., Chen, R. and Liu, J. S. (2013). Lookahead strategies for sequential Monte Carlo. Statist. Sci. 28, 69–94.10.1214/12-STS401CrossRefGoogle Scholar
Liu, J. S. (1991). Correlation structure and convergence rate of the Gibbs sampler. Doctoral Thesis, University of Chicago.Google Scholar
Liu, J. S. (1996). Metropolized independent sampling with comparisons to rejection sampling and importance sampling. Statist. Comput. 6, 113–119.CrossRefGoogle Scholar
Mengersen, K. L. and Tweedie, R. L. (1996). Rates of convergence of the Hastings and Metropolis algorithms. Ann. Statist 24, 101–121.Google Scholar
Mira, A. (1998). Ordering, slicing and splitting Monte Carlo Markov chains. Doctoral Thesis, University of Minnesota.Google Scholar
Pal, S. and Coates, M. (2018). Sequential MCMC with the discrete bouncy particle sampler. In IEEE Statistical Signal Processing Workshop (SSP), IEEE, pp. 663–667.10.1109/SSP.2018.8450772CrossRefGoogle Scholar
Pitt, M. K. and Shephard, N. (1999). Filtering via simulation: Auxiliary particle filters. J. Amer. Statist. Soc. 94, 590–599.10.1080/01621459.1999.10474153CrossRefGoogle Scholar
Rudolf, D. and Ullrich, M. (2013). Positivity of hit-and-run and related algorithms. Electron. Commun. Prob. 18, 1–8.10.1214/ECP.v18-2507CrossRefGoogle Scholar
Septier, F., Pang, S. K., Carmi, A. and Godsill, S. (2009). On MCMC-based particle methods for Bayesian filtering: application to multitarget tracking. In 3rd IEEE International Workshop on Computational Advances in Multi-Sensor Adaptive Processing (CAMSAP), IEEE, pp. 360–363.10.1109/CAMSAP.2009.5413256CrossRefGoogle Scholar
Septier, F. and Peters, G. W. (2016). Langevin and Hamiltonian based sequential MCMC for efficient Bayesian filtering in high-dimensional spaces. IEEE J. Sel. Top. Signal Processing 10, 312–327.10.1109/JSTSP.2015.2497211CrossRefGoogle Scholar
Shestopaloff, A. Y. and Neal, R. M. (2018). Sampling latent states for high-dimensional non-linear state space models with the embedded HMM method. Bayesian Anal. 13, 797–822.10.1214/17-BA1077CrossRefGoogle Scholar
Shiryaev, A. N. (1995). Probability, 2nd edn. Springer, New York.Google Scholar
Snyder, C., Bengtsson, T. and Morzfeld, M. (2015). Performance bounds for particle filters using the optimal proposal. Mon. Weather Rev. 143, 4750–4761.CrossRefGoogle Scholar
Whiteley, N. (2013). Stability properties of some particle filters. Ann. Appl. Prob. 23, 2500–2537.CrossRefGoogle Scholar