Hostname: page-component-6766d58669-6mz5d Total loading time: 0 Render date: 2026-05-24T02:14:24.599Z Has data issue: false hasContentIssue false
  • English
  • Français

Moran models and Wright–Fisher diffusions with selection and mutation in a one-sided random environment

Part of: Markov processes Time-dependent statistical mechanics (dynamic and nonequilibrium)

Published online by Cambridge University Press:  09 March 2023

Fernando Cordero Open the ORCID record for Fernando Cordero [Opens in a new window]  and
Grégoire Véchambre Open the ORCID record for Grégoire Véchambre [Opens in a new window]
Fernando Cordero*
Affiliation:
Bielefeld University
Grégoire Véchambre*
Affiliation:
Academy of Mathematics and Systems Science, Chinese Academy of Sciences
*
*Postal address: Faculty of Technology, Bielefeld University, Box 100131, 33501 Bielefeld, Germany. Email address: fcordero@techfak.uni-bielefeld.de
**Postal address: Academy of Mathematics and Systems Science, Chinese Academy of Sciences, No. 55, Zhongguancun East Road, Haidian District, Beijing, China. Email address: vechambre@amss.ac.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

Consider a two-type Moran population of size N with selection and mutation, where the selective advantage of the fit individuals is amplified at extreme environmental conditions. Assume selection and mutation are weak with respect to N, and extreme environmental conditions rarely occur. We show that, as 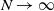$N\to\infty$, the type frequency process with time sped up by N converges to the solution to a Wright–Fisher-type SDE with a jump term modeling the effect of the environment. We use an extension of the ancestral selection graph (ASG) to describe the genealogical picture of the model. Next, we show that the type frequency process and the line-counting process of a pruned version of the ASG satisfy a moment duality. This relation yields a characterization of the asymptotic type distribution. We characterize the ancestral type distribution using an alternative pruning of the ASG. Most of our results are stated in annealed and quenched form.

Keywords

Wright–Fisher diffusionMoran modelrandom environmentancestral selection graphduality

MSC classification

Primary: 82C22: Interacting particle systems 92D15: Problems related to evolution
Secondary: 60J25: Continuous-time Markov processes on general state spaces 60J27: Continuous-time Markov processes on discrete state spaces

Information

Type
Original Article
Information
Advances in Applied Probability , Volume 55 , Issue 3 , September 2023 , pp. 701 - 767
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of Applied Probability Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Baake, E., Cordero, F. and Hummel, S. (2022). Lines of descent in the deterministic mutation-selection model with pairwise interaction. Ann. Appl. Prob. 32, 2400–2447.10.1214/21-AAP1736CrossRefGoogle Scholar
Baake, E., Lenz, U. and Wakolbinger, A. (2016). The common ancestor type distribution of a $\Lambda$ -Wright–Fisher process with selection and mutation. Electron. Commun. Prob. 21, 16 pp.10.1214/16-ECP16CrossRefGoogle Scholar
Baake, E. and Wakolbinger, A. (2018). Lines of descent under selection. J. Statist. Phys. 172, 156–174.10.1007/s10955-017-1921-9CrossRefGoogle Scholar
Bansaye, V., Caballero, M.-E. and Méléard, S. (2019). Scaling limits of population and evolution processes in random environment. Electron. J. Prob. 24, 38 pp.10.1214/19-EJP262CrossRefGoogle Scholar
Bansaye, V., Kurtz, T. G. and Simatos, F. (2016). Tightness for processes with fixed points of discontinuities and applications in varying environment. Electron. Commun. Prob. 21, 9 pp.10.1214/16-ECP6CrossRefGoogle Scholar
Barczy, M., Li, Z. and Pap, G. (2015). Yamada–Watanabe results for stochastic differential equations with jumps. Internat. J. Stoch. Anal. 2015, article no. 460472, 23 pp.Google Scholar
Biswas, N., Etheridge, A. and Klimek, A. (2021). The spatial Lambda-Fleming–Viot process with fluctuating selection. Electron. J. Prob. 26, 51 pp.10.1214/21-EJP593CrossRefGoogle Scholar
Bull, J. J. (1987). Evolution of phenotypic variance. Evolution 41, 303–315.10.2307/2409140CrossRefGoogle ScholarPubMed
Bürger, R. and Gimelfarb, A. (2002). Fluctuating environments and the role of mutation in maintaining quantitative genetic variation. Genet. Res. 80, 31–46.10.1017/S0016672302005682CrossRefGoogle ScholarPubMed
Chetwynd-Diggle, J. and Klimek, A. (2019). Rare mutations in the spatial Lambda-Fleming–Viot model in a fluctuating environment and SuperBrownian motion. Preprint. Available at https://arxiv.org/abs/1901.04374.Google Scholar
Cordero, F. (2017). Common ancestor type distribution: a Moran model and its deterministic limit. Stoch. Process. Appl. 127, 590–621.10.1016/j.spa.2016.06.019CrossRefGoogle Scholar
Cordero, F., Hummel, S. and Schertzer, E. (2022). General selection models: Bernstein duality and minimal ancestral structures. Ann. Appl. Prob. 32, 1499–1556.10.1214/21-AAP1683CrossRefGoogle Scholar
Cordero, F. and Möhle, M. (2019). On the stationary distribution of the block counting process for population models with mutation and selection. J. Math. Anal. Appl. 474, 1049–1081.10.1016/j.jmaa.2019.02.004CrossRefGoogle Scholar
Dynkin, E. B. (1965). Markov Processes, Vol. 1. Springer, Berlin, Heidelberg.Google Scholar
Etheridge, A. M., Griffiths, R. C. and Taylor, J. E. (2010). A coalescent dual process in a Moran model with genic selection, and the lambda coalescent limit. Theoret. Pop. Biol. 78, 77–92.10.1016/j.tpb.2010.05.004CrossRefGoogle Scholar
Foucart, C. (2013). The impact of selection in the $\Lambda$ -Wright–Fisher model. Electron. Commun. Prob. 18, 10 pp.10.1214/ECP.v18-2838CrossRefGoogle Scholar
Fu, Z. and Li, Z. (2010). Stochastic equations of non-negative processes with jumps. Stoch. Process. Appl. 120, 306–330.10.1016/j.spa.2009.11.005CrossRefGoogle Scholar
Gillespie, J. H. (1972). The effects of stochastic environments on allele frequencies in natural populations. Theoret. Pop. Biol. 3, 241–248.10.1016/0040-5809(72)90001-9CrossRefGoogle ScholarPubMed
González Casanova, A. and Spanò, D. (2018). Duality and fixation in $\Xi$ -Wright–Fisher processes with frequency-dependent selection. Ann. Appl. Prob. 28, 250–284.Google Scholar
González Casanova, A., Spanò, D. and Wilke-Berenguer, M. (2019). The effective strength of selection in random environment. Preprint. Available at https://arxiv.org/abs/1903.12121.Google Scholar
Guillin, A., Jabot, F. and Personne, A. (2020). On the Simpson index for the Moran process with random selection and immigration. Internat. J. Biomath. 13, article no. 2050046.10.1142/S1793524520500461CrossRefGoogle Scholar
Guillin, A., Personne, A. and Strickler, E. (2019). Persistence in the Moran model with random switching. Preprint. Available at https://arxiv.org/abs/1911.01108.Google Scholar
Jansen, S. and Kurt, N. (2014). On the notion(s) of duality for Markov processes. Prob. Surveys 11, 59–120.10.1214/12-PS206CrossRefGoogle Scholar
Kallenberg, O. (2021). Foundations of Modern Probability, 3rd edn. Springer, Cham.10.1007/978-3-030-61871-1CrossRefGoogle Scholar
Karlin, S. and Benny Levikson, B. (1974). Temporal fluctuations in selection intensities: case of small population size. Theoret. Pop. Biol. 6, 383–412.10.1016/0040-5809(74)90017-3CrossRefGoogle Scholar
Karlin, S. and Liberman, U. (1975). Random temporal variation in selection intensities: one-locus two-allele model. J. Math. Biol. 2, 1–17.10.1007/BF00276012CrossRefGoogle Scholar
Karlin, S. and Lieberman, U. (1974). Random temporal variation in selection intensities: Case of large population size. Theoret. Pop. Biol. 6, 355–382.10.1016/0040-5809(74)90016-1CrossRefGoogle ScholarPubMed
Kimura, M. (1962). On the probability of fixation of mutant genes in a population. Genetics 47, 713–719.10.1093/genetics/47.6.713CrossRefGoogle ScholarPubMed
Krone, S. M. and Neuhauser, C. (1997). Ancestral processes with selection. Theoret. Pop. Biol. 51, 210–237.10.1006/tpbi.1997.1299CrossRefGoogle ScholarPubMed
Kurtz, T. G. (2011). Equivalence of stochastic equations and martingale problems. In Stochastic Analysis 2010, ed. D. Crisan, Springer, Berlin, pp. 113–130.10.1007/978-3-642-15358-7_6CrossRefGoogle Scholar
Lenz, U., Kluth, S., Baake, E. and Wakolbinger, A. (2015). Looking down in the ancestral selection graph: a probabilistic approach to the common ancestor type distribution. Theoret. Pop. Biol. 103, 27–37.10.1016/j.tpb.2015.01.005CrossRefGoogle Scholar
Li, Z. and Pu, F. (2012). Strong solutions of jump-type stochastic equations. Electron. Commun. Prob. 17, 13 pp.10.1214/ECP.v17-1915CrossRefGoogle Scholar
Möhle, M. (2001). Forward and backward diffusion approximations for haploid exchangeable population models. Stoch. Process. Appl. 95, 133–149.10.1016/S0304-4149(01)00093-XCrossRefGoogle Scholar
Neuhauser, C. (1999). The ancestral graph and gene genealogy under frequency-dependent selection. Theoret. Pop. Biol. 56, 203–214.10.1006/tpbi.1999.1412CrossRefGoogle ScholarPubMed
Neuhauser, C. and Krone, S. M. (1997). The genealogy of samples in models with selection. Genetics 145, 519–534.10.1093/genetics/145.2.519CrossRefGoogle ScholarPubMed
Sagitov, S., Jagers, P. and Vatutin, V. (2010). Coalescent approximation for structured populations in a stationary random environment. Theoret. Pop. Biol. 78, 192–199.10.1016/j.tpb.2010.06.008CrossRefGoogle Scholar
Van Casteren, J. A. (1992). On martingales and Feller semigroups. Results Math. 21, 274–288.10.1007/BF03323085CrossRefGoogle Scholar