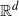1. Introduction
Limit theorems of functionals of Poisson point processes initiated by Avram and Bertsimas [Reference Avram and Bertsimas1] have been of considerable interest in the literature; see, e.g., [Reference Lachièze-Rey, Schulte and Yukich30, Reference Last, Peccati and Schulte31, Reference Peccati, Solé, Taqqu and Utzet37, Reference Reitzner and Schulte41, Reference Schulte46, Reference Schulte47] and references therein. To estimate the approximation errors, a number of tools have been developed, including Stein’s method [Reference Barbour3, Reference Barbour and Brown4], the Malliavin–Stein technique via the Wiener–Itô expansion [Reference Peccati, Solé, Taqqu and Utzet37] and the second-order Poincaré inequalities [Reference Last, Peccati and Schulte31], and the stabilisation [Reference Penrose and Yukich38, Reference Penrose and Yukich39]. The main feature of the stabilisation is that the insertion of a point into a Poisson point process induces only a local effect, in some sense; hence there is little change in the functionals. However, inserting an additional point into the Poisson point process results in the Palm process of the Poisson point process at the point [Reference Kallenberg26, Chapter 10], and it is shown in [Reference Chen, Röllin and Xia13, Reference Chen and Xia14] that the magnitude of the difference between a point process and its Palm processes is directly linked to the accuracy of Poisson and normal approximations of the point process. This is also the fundamental reason why the limit theorems in the above-mentioned papers can be established.
The normal approximation theory is generally quantified in terms of the Kolmogorov distance
![]() $d_K$
: for two random variables
$d_K$
: for two random variables
![]() $X_1$
and
$X_1$
and
![]() $X_2$
with distributions
$X_2$
with distributions
![]() $F_1$
and
$F_1$
and
![]() $F_2$
,
$F_2$
,
The well-known Berry–Esseen theorem [Reference Berry7, Reference Esseen20] states the following. If
![]() $X_i$
,
$X_i$
,
![]() $1\le i\le n,$
are independent and identically distributed (i.i.d.) random variables with mean 0, variance 1, and a finite third moment, define
$1\le i\le n,$
are independent and identically distributed (i.i.d.) random variables with mean 0, variance 1, and a finite third moment, define
where
![]() $\sim$
denotes ‘is distributed as’. Then
$\sim$
denotes ‘is distributed as’. Then
The Kolmogorov distance
![]() $d_K(F_1,F_2)$
measures the maximum difference between the distribution functions
$d_K(F_1,F_2)$
measures the maximum difference between the distribution functions
![]() $F_1$
and
$F_1$
and
![]() $F_2$
, but it does not say much about the difference between the probabilities
$F_2$
, but it does not say much about the difference between the probabilities
![]() $\mathbb{P}(X_1\in A)$
and
$\mathbb{P}(X_1\in A)$
and
![]() $\mathbb{P}(X_2\in A)$
for a non-interval Borel subset A of the real space
$\mathbb{P}(X_2\in A)$
for a non-interval Borel subset A of the real space
![]() $\mathbb{R}$
, e.g.,
$\mathbb{R}$
, e.g.,
![]() $A=\cup_{i\in \mathbb{Z}}(2i,2i+0.5]$
, where
$A=\cup_{i\in \mathbb{Z}}(2i,2i+0.5]$
, where
![]() $\mathbb{Z}$
denotes the set of all integers. Such information is reflected in the total variation distance
$\mathbb{Z}$
denotes the set of all integers. Such information is reflected in the total variation distance
![]() $d_{TV}(F_1,F_2)$
, defined by
$d_{TV}(F_1,F_2)$
, defined by
where
![]() ${\mathscr{B}}(\mathbb{R})$
stands for the Borel
${\mathscr{B}}(\mathbb{R})$
stands for the Borel
![]() $\sigma$
-algebra on
$\sigma$
-algebra on
![]() $\mathbb{R}$
. Vanishing bounds for normal approximation under the total variation distance for statistics in geometric probability provide us with the theoretical foundation for constructing density estimators of the distributions in a wide range of applications documented in [Reference Chiu, Stoyan, Kendall and Mecke15, Chapters 8--10] and bound the minimax probability of error for making statistical inference [Reference Tsybakov49, pp. 80--81]. Moreover, since
$\mathbb{R}$
. Vanishing bounds for normal approximation under the total variation distance for statistics in geometric probability provide us with the theoretical foundation for constructing density estimators of the distributions in a wide range of applications documented in [Reference Chiu, Stoyan, Kendall and Mecke15, Chapters 8--10] and bound the minimax probability of error for making statistical inference [Reference Tsybakov49, pp. 80--81]. Moreover, since
![]() $d_{K}(X_1,X_2)\le d_{TV}(X_1,X_2)$
, vanishing bounds on the total variation distance imply a stronger qualitative result than just a central limit theorem (CLT).
$d_{K}(X_1,X_2)\le d_{TV}(X_1,X_2)$
, vanishing bounds on the total variation distance imply a stronger qualitative result than just a central limit theorem (CLT).
Although CLTs with errors measured in the total variation distance have been studied in some special circumstances (see, e.g., [Reference Diaconis and Freedman19, Reference Meckes and Meckes36, Reference Bally and Caramellino2]), it is generally believed that the total variation distance is too strong for quantifying the errors in normal approximation (see, e.g., [Reference Čekanavičius9, Reference Chen and Leong12, Reference Fang21]). For example, the total variation distance between any discrete distribution and any normal distribution is always 1. To recover CLTs with errors measured in the total variation distance, a common approach is to discretise the distribution of interest and approximate it with a simple discrete distribution, e.g., a translated Poisson distribution [Reference Röllin43, Reference Röllin44], a centred binomial distribution [Reference Röllin45], a discretised normal distribution [Reference Chen and Leong12, Reference Fang21], or a family of polynomial-type distributions [Reference Goldstein and Xia24]. The multivariate versions of these approximations are investigated by [Reference Barbour, Luczak and Xia6].
By discretising a distribution F of interest, we essentially group the probability of an area and put it at one point in the area. Hence the information of F(A) for a general set
![]() $A\in{\mathscr{B}}(\mathbb{R})$
is completely lost. In this paper, we consider the normal approximation in terms of the total variation distance to the sum of random variables under various circumstances.
$A\in{\mathscr{B}}(\mathbb{R})$
is completely lost. In this paper, we consider the normal approximation in terms of the total variation distance to the sum of random variables under various circumstances.
A motivating example: [Reference Feller22, p. 146]. Let
![]() $\{X_i\,:\, i\ge 1\}$
be a sequence of i.i.d. random variables taking values 0 and 1 with equal probability; then
$\{X_i\,:\, i\ge 1\}$
be a sequence of i.i.d. random variables taking values 0 and 1 with equal probability; then
![]() $X=\sum_{k=1}^\infty 2^{-k}X_k$
has the uniform distribution on (0, 1). If we separate the even and odd terms into
$X=\sum_{k=1}^\infty 2^{-k}X_k$
has the uniform distribution on (0, 1). If we separate the even and odd terms into
![]() $U=\sum_{k=1}^\infty 2^{-2k}X_{2k}$
and
$U=\sum_{k=1}^\infty 2^{-2k}X_{2k}$
and
![]() $V=\sum_{k=1}^\infty 2^{-(2k-1)}X_{2k-1}$
, then U and V are independent,
$V=\sum_{k=1}^\infty 2^{-(2k-1)}X_{2k-1}$
, then U and V are independent,
![]() . Both U and V differ only by scale factors from the Cantor distribution, which is singular with respect to the Lebesgue measure [Reference Feller22, p. 146]. Now, we can construct mutually independent random variables
. Both U and V differ only by scale factors from the Cantor distribution, which is singular with respect to the Lebesgue measure [Reference Feller22, p. 146]. Now, we can construct mutually independent random variables
![]() $\{U_i,\ V_i\,:\, i\ge 1\}$
such that
$\{U_i,\ V_i\,:\, i\ge 1\}$
such that
![]() $U_i\stackrel{\mbox{d}}{=} U-\mathbb{E} U$
and
$U_i\stackrel{\mbox{d}}{=} U-\mathbb{E} U$
and
![]() $V_i\stackrel{\mbox{d}}{=} V-\mathbb{E} V$
. Consider
$V_i\stackrel{\mbox{d}}{=} V-\mathbb{E} V$
. Consider
![]() $\xi_1=U_1+V_1$
,
$\xi_1=U_1+V_1$
,
![]() $\xi_2=-V_1-U_2$
,
$\xi_2=-V_1-U_2$
,
![]() $\xi_3=U_2+V_2$
,
$\xi_3=U_2+V_2$
,
![]() $\dots$
; then
$\dots$
; then
![]() $\{\xi_i\}$
is a sequence of 1-dependent and identically distributed random variables having the uniform distribution on
$\{\xi_i\}$
is a sequence of 1-dependent and identically distributed random variables having the uniform distribution on
![]() $({-}0.5,0.5)$
. One can easily verify that
$({-}0.5,0.5)$
. One can easily verify that
![]() $\sum_{i=1}^n\xi_i$
does not converge to normal as
$\sum_{i=1}^n\xi_i$
does not converge to normal as
![]() $n\to\infty$
; hence stronger conditions are needed to ensure normal approximation for the sum of dependent random variables.
$n\to\infty$
; hence stronger conditions are needed to ensure normal approximation for the sum of dependent random variables.
Under the Kolmogorov distance, user-friendly conditions are usually formulated to ensure that the variance of the sum becomes large as
![]() $n\to\infty$
. In the motivating example, the variance of the partial sum
$n\to\infty$
. In the motivating example, the variance of the partial sum
![]() $\sum_{i=1}^n\xi_i$
is bounded, which does not give sufficient offset in the
$\sum_{i=1}^n\xi_i$
is bounded, which does not give sufficient offset in the
![]() $\xi_i$
’s to warrant a CLT. For the normal approximation of the sum of score functions, a typical condition for the variance to converge to infinity sufficiently fast is non-degeneracy—that is, the conditional variance of the sum given the information outside a local region is away from 0 (see [Reference Penrose and Yukich38, Reference Xia and Yukich51]).
$\xi_i$
’s to warrant a CLT. For the normal approximation of the sum of score functions, a typical condition for the variance to converge to infinity sufficiently fast is non-degeneracy—that is, the conditional variance of the sum given the information outside a local region is away from 0 (see [Reference Penrose and Yukich38, Reference Xia and Yukich51]).
The success of normal approximation with errors measured in terms of the total variation distance without discretisation hinges on non-singularity; that is, the distribution contains an absolutely continuous component with respect to the Lebesgue measure. More precisely, by the Lebesgue decomposition theorem [Reference Halmos25, p. 134], any distribution function F on
![]() $\mathbb{R}$
can be represented as
$\mathbb{R}$
can be represented as
where
![]() $\alpha_F\in[0,1]$
, and where
$\alpha_F\in[0,1]$
, and where
![]() $F_s$
and
$F_s$
and
![]() $F_a$
are two distribution functions such that, with respect to the Lebesgue measure on
$F_a$
are two distribution functions such that, with respect to the Lebesgue measure on
![]() $\mathbb{R}$
,
$\mathbb{R}$
,
![]() $F_a$
is absolutely continuous and
$F_a$
is absolutely continuous and
![]() $F_s$
is singular [Reference Halmos25, p. 126]; F is said to be non-singular if
$F_s$
is singular [Reference Halmos25, p. 126]; F is said to be non-singular if
![]() $\alpha_F>0$
. For convenience, we say that a random variable is non-singular if its distribution function is non-singular. It is clear that non-singularity implies non-degeneracy. Prohorov [Reference Prohorov40] proved that in one dimension, a necessary and sufficient condition for the convergence of the standardised partial sum of i.i.d. random variables
$\alpha_F>0$
. For convenience, we say that a random variable is non-singular if its distribution function is non-singular. It is clear that non-singularity implies non-degeneracy. Prohorov [Reference Prohorov40] proved that in one dimension, a necessary and sufficient condition for the convergence of the standardised partial sum of i.i.d. random variables
![]() $X_i$
to the standard normal distribution in terms of the total variation distance is that there exists an
$X_i$
to the standard normal distribution in terms of the total variation distance is that there exists an
![]() $n_0\in \mathbb{N}$
such that
$n_0\in \mathbb{N}$
such that
![]() $\sum_{i=1}^{n_0}X_i$
is non-singular. The non-singularity is almost necessary because it is an essential ingredient in the special case of the sum of i.i.d. random variables; see [Reference Bally and Caramellino2] for a brief review of the development of the CLT in the total variation distance.
$\sum_{i=1}^{n_0}X_i$
is non-singular. The non-singularity is almost necessary because it is an essential ingredient in the special case of the sum of i.i.d. random variables; see [Reference Bally and Caramellino2] for a brief review of the development of the CLT in the total variation distance.
In the context of functionals of Poisson point processes, a prototypical example is the sum
![]() $W_\nu=\sum_{i=1}^NX_i$
of Poisson number
$W_\nu=\sum_{i=1}^NX_i$
of Poisson number
![]() $N\sim{\textrm{Poisson}}(\nu)$
i.i.d. random variables
$N\sim{\textrm{Poisson}}(\nu)$
i.i.d. random variables
![]() $\{X_i,\ i\ge 1\}$
which are independent of N. If the distribution
$\{X_i,\ i\ge 1\}$
which are independent of N. If the distribution
![]() $\mathscr{L}(X_1)$
of
$\mathscr{L}(X_1)$
of
![]() $X_1$
is discrete, then the distribution of
$X_1$
is discrete, then the distribution of
![]() $W_{s,\nu}\,:\!=\,(W_\nu-\mathbb{E}W_\nu)/\sqrt{{\textrm{Var}}(W_\nu)}$
is also discrete, and hence
$W_{s,\nu}\,:\!=\,(W_\nu-\mathbb{E}W_\nu)/\sqrt{{\textrm{Var}}(W_\nu)}$
is also discrete, and hence
![]() $d_{TV}(W_{s,\nu},Z)=1$
for all
$d_{TV}(W_{s,\nu},Z)=1$
for all
![]() $\nu$
, where
$\nu$
, where
![]() $Z\sim N(0,1)$
. However, if
$Z\sim N(0,1)$
. However, if
![]() $\mathscr{L}(X_1)$
is non-singular, the asymptotic behaviour of
$\mathscr{L}(X_1)$
is non-singular, the asymptotic behaviour of
![]() $d_{TV}(W_{s,\nu},Z)$
in terms of large
$d_{TV}(W_{s,\nu},Z)$
in terms of large
![]() $\nu$
is very similar to that of
$\nu$
is very similar to that of
![]() $d_{K}(W_{s,\nu},Z)$
. For example, assume that
$d_{K}(W_{s,\nu},Z)$
. For example, assume that
![]() $\mathbb{P}(Y_1=1)=9/10$
and
$\mathbb{P}(Y_1=1)=9/10$
and
![]() $\mathbb{P}(Y_1\in dx)=0.1 dx$
for
$\mathbb{P}(Y_1\in dx)=0.1 dx$
for
![]() $x\in [0,1)$
. Then Figure 1 shows that when
$x\in [0,1)$
. Then Figure 1 shows that when
![]() $\nu=50$
, the density function of the absolutely continuous part of
$\nu=50$
, the density function of the absolutely continuous part of
![]() $W_{s,\nu}$
is very close to that of N (0, 1) in the total variation distance, giving a very small value of
$W_{s,\nu}$
is very close to that of N (0, 1) in the total variation distance, giving a very small value of
![]() $d_{TV}(W_{s,\nu},Z)$
. Moreover, as shown in Figure 2, the distance
$d_{TV}(W_{s,\nu},Z)$
. Moreover, as shown in Figure 2, the distance
![]() $d_{TV}(W_{s,\nu},Z)$
decreases very fast when
$d_{TV}(W_{s,\nu},Z)$
decreases very fast when
![]() $\nu$
becomes large. Briefly summarised, the main results of the paper state that, for the score functions of samples arising from random events driven by a marked Poisson point process on
$\nu$
becomes large. Briefly summarised, the main results of the paper state that, for the score functions of samples arising from random events driven by a marked Poisson point process on
![]() $\mathbb{R}^d$
, if the conditional distribution of the sum given the information outside a neighbourhood is non-singular, then, with the cost of a logarithmic factor, the error of the normal approximation to the sum of such score functions in terms of the total variation distance is similar to the error with respect to the Kolmogorov distance established in, e.g., [Reference Penrose and Yukich38, Reference Penrose and Yukich39, Reference Lachièze-Rey, Schulte and Yukich30].
$\mathbb{R}^d$
, if the conditional distribution of the sum given the information outside a neighbourhood is non-singular, then, with the cost of a logarithmic factor, the error of the normal approximation to the sum of such score functions in terms of the total variation distance is similar to the error with respect to the Kolmogorov distance established in, e.g., [Reference Penrose and Yukich38, Reference Penrose and Yukich39, Reference Lachièze-Rey, Schulte and Yukich30].

Figure 1.
![]() $\nu=50$
.
$\nu=50$
.

Figure 2.
![]() $\nu=100$
.
$\nu=100$
.
In Section 2, we give definitions of the concepts, state the conditions, and present the main theorems. In Section 3, these theorems are applied to establish error bounds for the normal approximation for statistics in Voronoi tessellations, k-nearest-neighbours graphs, timber volume, and maximal layers. The proofs of the main results in Section 2 rely on a number of preliminaries and lemmas which are given in Section 4. For ease of reading, all proofs are postponed to Section 5.
2. General results
We consider the functionals of a marked point process with a Poisson point process in
![]() $\mathbb{R}^d$
as its ground process, and each point carries a mark in a measurable space
$\mathbb{R}^d$
as its ground process, and each point carries a mark in a measurable space
![]() $(T,\mathscr{T})$
independently of other marks, where
$(T,\mathscr{T})$
independently of other marks, where
![]() $\mathscr{T}$
is a
$\mathscr{T}$
is a
![]() $\sigma$
-algebra on T. More precisely, let
$\sigma$
-algebra on T. More precisely, let
![]() $\textbf{S}\,:\!=\,\mathbb{R}^d\times T$
be equipped with the product
$\textbf{S}\,:\!=\,\mathbb{R}^d\times T$
be equipped with the product
![]() $\sigma$
-field
$\sigma$
-field
![]() $\mathscr{S}\,:\!=\,\mathscr{B}\big(\mathbb{R}^d\big)\times \mathscr{T}$
, where
$\mathscr{S}\,:\!=\,\mathscr{B}\big(\mathbb{R}^d\big)\times \mathscr{T}$
, where
![]() $\mathscr{B}\big(\mathbb{R}^d\big)$
is the Borel
$\mathscr{B}\big(\mathbb{R}^d\big)$
is the Borel
![]() $\sigma$
-algebra of
$\sigma$
-algebra of
![]() $\mathbb{R}^d$
. We use
$\mathbb{R}^d$
. We use
![]() $\boldsymbol{C}_{\boldsymbol{S}}$
to denote the space of all locally finite non-negative integer-valued measures
$\boldsymbol{C}_{\boldsymbol{S}}$
to denote the space of all locally finite non-negative integer-valued measures
![]() $\xi$
, often called configurations, on
$\xi$
, often called configurations, on
![]() $\boldsymbol{S}$
such that
$\boldsymbol{S}$
such that
![]() $\xi(\{{x}\}\times T)\le 1$
for all
$\xi(\{{x}\}\times T)\le 1$
for all
![]() ${x}\in\mathbb{R}^d$
. The space
${x}\in\mathbb{R}^d$
. The space
![]() $\boldsymbol{C}_{\boldsymbol{S}}$
is endowed with the
$\boldsymbol{C}_{\boldsymbol{S}}$
is endowed with the
![]() $\sigma$
-field
$\sigma$
-field
![]() $\mathscr{C}_{\boldsymbol{S}}$
generated by the vague topology [Reference Kallenberg26, p. 169]. A marked point process
$\mathscr{C}_{\boldsymbol{S}}$
generated by the vague topology [Reference Kallenberg26, p. 169]. A marked point process
![]() $\Xi$
is a measurable mapping from
$\Xi$
is a measurable mapping from
![]() $(\Omega,\mathscr{F},\mathbb{P})$
to
$(\Omega,\mathscr{F},\mathbb{P})$
to
![]() $(\boldsymbol{C}_{\boldsymbol{S}},\mathscr{C}_{\boldsymbol{S}})$
[Reference Kallenberg27, p. 49]. The induced simple point process
$(\boldsymbol{C}_{\boldsymbol{S}},\mathscr{C}_{\boldsymbol{S}})$
[Reference Kallenberg27, p. 49]. The induced simple point process
![]() $\bar\Xi({\cdot})\,:\!=\,\Xi({\cdot}\times T)$
is called the ground process [Reference Daley and Vere-Jones16, p. 3] or projection [Reference Kallenberg27, p. 17] of the marked point process
$\bar\Xi({\cdot})\,:\!=\,\Xi({\cdot}\times T)$
is called the ground process [Reference Daley and Vere-Jones16, p. 3] or projection [Reference Kallenberg27, p. 17] of the marked point process
![]() $\Xi$
on
$\Xi$
on
![]() $\mathbb{R}^d$
. In this paper, we use
$\mathbb{R}^d$
. In this paper, we use
![]() $\mathscr{P}_{\lambda,\mathscr{L}_T}$
to denote the law of a marked Poisson point process having a homogeneous Poisson point process on
$\mathscr{P}_{\lambda,\mathscr{L}_T}$
to denote the law of a marked Poisson point process having a homogeneous Poisson point process on
![]() $\mathbb{R}^d$
with intensity measure
$\mathbb{R}^d$
with intensity measure
![]() $\lambda dx$
as its ground process and i.i.d. marks on
$\lambda dx$
as its ground process and i.i.d. marks on
![]() $(T,\mathscr{T})$
with the law
$(T,\mathscr{T})$
with the law
![]() $\mathscr{L}_T$
.
$\mathscr{L}_T$
.
For convenience, we write the restricted process of
![]() $\Xi$
on a measurable set
$\Xi$
on a measurable set
![]() $A\in \mathscr{B}\big(\mathbb{R}^d\big)$
as
$A\in \mathscr{B}\big(\mathbb{R}^d\big)$
as
![]() $\Xi_A$
, i.e.,
$\Xi_A$
, i.e.,
![]() $\Xi_A(B\times D)\,:\!=\,\Xi((A\cap B)\times D)$
for all
$\Xi_A(B\times D)\,:\!=\,\Xi((A\cap B)\times D)$
for all
![]() $D\in \mathscr{T}$
and
$D\in \mathscr{T}$
and
![]() $B\in \mathscr{B}\big(\mathbb{R}^d\big)$
. Statistics in geometric probability are often affected by the point configuration; hence both the restricted and unrestricted point patterns are of interest in applications. The functionals we study in the paper are defined on
$B\in \mathscr{B}\big(\mathbb{R}^d\big)$
. Statistics in geometric probability are often affected by the point configuration; hence both the restricted and unrestricted point patterns are of interest in applications. The functionals we study in the paper are defined on
![]() $\Gamma_\alpha\,:\!=\,\left[-\frac{1}{2}\alpha^{\frac{1}{d}}, \frac{1}{2}\alpha^{\frac{1}{d}}\right]^d$
and have the forms
$\Gamma_\alpha\,:\!=\,\left[-\frac{1}{2}\alpha^{\frac{1}{d}}, \frac{1}{2}\alpha^{\frac{1}{d}}\right]^d$
and have the forms
and
where
![]() $\Xi\sim\mathscr{P}_{\lambda,\mathscr{L}_T}.$
The function
$\Xi\sim\mathscr{P}_{\lambda,\mathscr{L}_T}.$
The function
![]() $\eta$
is called a score function (resp. restricted score function), i.e., a measurable function on
$\eta$
is called a score function (resp. restricted score function), i.e., a measurable function on
![]() $\left(\boldsymbol{S}\times \boldsymbol{C}_{\boldsymbol{S}},\mathscr{S} \times \mathscr{C}_{\boldsymbol{S}}\right)$
to
$\left(\boldsymbol{S}\times \boldsymbol{C}_{\boldsymbol{S}},\mathscr{S} \times \mathscr{C}_{\boldsymbol{S}}\right)$
to
![]() $\left(\mathbb{R},\mathscr{B}\!\left(\mathbb{R}\right)\right)$
(resp. a function mapping
$\left(\mathbb{R},\mathscr{B}\!\left(\mathbb{R}\right)\right)$
(resp. a function mapping
![]() $\boldsymbol{S}\times \boldsymbol{C}_{\boldsymbol{S}}\times {\mathscr{B}\!\left(\mathbb{R}^d\right)}$
to
$\boldsymbol{S}\times \boldsymbol{C}_{\boldsymbol{S}}\times {\mathscr{B}\!\left(\mathbb{R}^d\right)}$
to
![]() $\mathbb{R}$
which is measurable with respect to
$\mathbb{R}$
which is measurable with respect to
![]() $(\mathscr{S}\cap (\Gamma_\alpha\times T) )\times \mathscr{C}_{\boldsymbol{S}\cap (\Gamma_\alpha\times T)}\rightarrow \mathscr{B}(\mathbb{R})$
when the third coordinate is fixed), and it represents the interaction between a point and the configuration. Because our interest is in the values of the score function of the points in a configuration, for convenience,
$(\mathscr{S}\cap (\Gamma_\alpha\times T) )\times \mathscr{C}_{\boldsymbol{S}\cap (\Gamma_\alpha\times T)}\rightarrow \mathscr{B}(\mathbb{R})$
when the third coordinate is fixed), and it represents the interaction between a point and the configuration. Because our interest is in the values of the score function of the points in a configuration, for convenience,
![]() $\eta\!\left((x,m),\mathscr{X}\right){(\mbox{resp.}\,\eta\!\left((x,m),\mathscr{X},\Gamma_\alpha\right))}$
is understood as 0 for all
$\eta\!\left((x,m),\mathscr{X}\right){(\mbox{resp.}\,\eta\!\left((x,m),\mathscr{X},\Gamma_\alpha\right))}$
is understood as 0 for all
![]() $x\in \mathbb{R}^d$
and
$x\in \mathbb{R}^d$
and
![]() $\mathscr{X}\in \boldsymbol{C}_{\boldsymbol{S}}$
such that
$\mathscr{X}\in \boldsymbol{C}_{\boldsymbol{S}}$
such that
![]() $(x,m)\notin \mathscr{X}$
. We consider the score functions satisfying the following four conditions:
$(x,m)\notin \mathscr{X}$
. We consider the score functions satisfying the following four conditions:
-
stabilisation (Assumption 2.1)
-
translation-invariance (Assumption 2.2)
-
a moment condition (Assumption 2.3)
-
non-singularity (Assumption 2.4)
Assumption 2.1. Stabilisation
Unrestricted case. For a locally finite configuration
![]() $\mathscr{X}$
and
$\mathscr{X}$
and
![]() $z\in (\mathbb{R}^d\times T)\cup\{\emptyset\}$
, write
$z\in (\mathbb{R}^d\times T)\cup\{\emptyset\}$
, write
![]() if
if
![]() $z=\emptyset$
and
$z=\emptyset$
and
![]() otherwise. We use
otherwise. We use
![]() $\delta_v$
to denote the Dirac measure at v, and B(x, r) to denote the ball with centre x and radius r. The notion of stabilisation is introduced in [Reference Penrose and Yukich38], and we adapt it to our setup as follows.
$\delta_v$
to denote the Dirac measure at v, and B(x, r) to denote the ball with centre x and radius r. The notion of stabilisation is introduced in [Reference Penrose and Yukich38], and we adapt it to our setup as follows.
Definition 2.1.
(Unrestricted case.) A score function
![]() $\eta$
on
$\eta$
on
![]() $\mathbb{R}^d\times T$
is range-bounded (resp. exponentially stabilising, polynomially stabilising of order
$\mathbb{R}^d\times T$
is range-bounded (resp. exponentially stabilising, polynomially stabilising of order
![]() $\beta>0$
) with respect to intensity
$\beta>0$
) with respect to intensity
![]() $\lambda$
and a probability measure
$\lambda$
and a probability measure
![]() $\mathscr{L}_T$
on T if for all
$\mathscr{L}_T$
on T if for all
![]() $x\in \mathbb{R}^d$
,
$x\in \mathbb{R}^d$
,
![]() $z\in (\mathbb{R}^d\times T)\cup\{\emptyset\}$
, and almost all realisations
$z\in (\mathbb{R}^d\times T)\cup\{\emptyset\}$
, and almost all realisations
![]() $\mathscr{X}$
of the marked homogeneous Poisson point process
$\mathscr{X}$
of the marked homogeneous Poisson point process
![]() $\Xi\sim\mathscr{P}_{\lambda,\mathscr{L}_T}$
, there exists an
$\Xi\sim\mathscr{P}_{\lambda,\mathscr{L}_T}$
, there exists an
(a radius of stabilisation) such that for all locally finite
, we have

and the tail probability
satisfies
for some positive constants
![]() $C_1$
and
$C_1$
and
![]() $C_2$
.
$C_2$
.
Here and in the following, we write R or R(x) (resp.
![]() $\bar{R}$
or
$\bar{R}$
or
![]() $\bar{R}(x)$
in Definition 2.1) only if it will not cause any confusion. The definition ensures that
$\bar{R}(x)$
in Definition 2.1) only if it will not cause any confusion. The definition ensures that
![]() is determined by
is determined by
![]() $\mathscr{X}_{B(x,t)}$
for all
$\mathscr{X}_{B(x,t)}$
for all
![]() $x\in \mathbb{R}^d$
and
$x\in \mathbb{R}^d$
and
![]() $t\in \mathbb{R}_+.$
$t\in \mathbb{R}_+.$
Restricted case. We have the following counterpart of stabilisation for the functionals with a restricted marked Poisson point process input. Note that the score function for the restricted input is not affected by points outside
![]() $\Gamma_\alpha$
.
$\Gamma_\alpha$
.
Definition 2.2.
(Restricted case.) A score function
![]() $\eta$
is range-bounded (resp. exponentially stabilising, polynomially stabilising of order
$\eta$
is range-bounded (resp. exponentially stabilising, polynomially stabilising of order
![]() $\beta>0$
) with respect to intensity
$\beta>0$
) with respect to intensity
![]() $\lambda$
and a probability measure
$\lambda$
and a probability measure
![]() $\mathscr{L}_T$
on T if for all
$\mathscr{L}_T$
on T if for all
![]() $\alpha\in \mathbb{R}_+$
,
$\alpha\in \mathbb{R}_+$
,
![]() $x\in \Gamma_\alpha$
, and
$x\in \Gamma_\alpha$
, and
![]() $z\in (\Gamma_\alpha \times T)\cup\{\emptyset\}$
, and almost all realisations
$z\in (\Gamma_\alpha \times T)\cup\{\emptyset\}$
, and almost all realisations
![]() $\mathscr{X}$
of the marked homogeneous Poisson point process
$\mathscr{X}$
of the marked homogeneous Poisson point process
![]() $\Xi\sim\mathscr{P}_{\lambda,\mathscr{L}_T}$
, there exists an
$\Xi\sim\mathscr{P}_{\lambda,\mathscr{L}_T}$
, there exists an
(a radius of stabilisation) such that for all locally finite
![]() $\mathscr{Y}\subset (\Gamma_\alpha\backslash B(x,R))\times T$
, we have
$\mathscr{Y}\subset (\Gamma_\alpha\backslash B(x,R))\times T$
, we have

and the tail probability
satisfies
for some positive constants
![]() $C_1$
and
$C_1$
and
![]() $C_2$
.
$C_2$
.
As in the unrestricted case, the definition ensures that
![]() is a function of
is a function of
![]() $\mathscr{X}_{B(x,t)\cap \Gamma_{\alpha}}$
for all
$\mathscr{X}_{B(x,t)\cap \Gamma_{\alpha}}$
for all
![]() $x\in \mathbb{R}^d$
and
$x\in \mathbb{R}^d$
and
![]() $\alpha, t\in \mathbb{R}_+.$
$\alpha, t\in \mathbb{R}_+.$
Assumption 2.2. Translation-invariance
We write
![]() $d(x,A)\,:\!=\,\inf\{d(x,y);\,y\in A\}$
,
$d(x,A)\,:\!=\,\inf\{d(x,y);\,y\in A\}$
,
![]() $A\pm B\,:\!=\,\{x\pm y; \, x\in A,\ y\in B\}$
for
$A\pm B\,:\!=\,\{x\pm y; \, x\in A,\ y\in B\}$
for
![]() $x\in \mathbb{R}^d$
and
$x\in \mathbb{R}^d$
and
![]() $A,B\in\mathscr{B}\!\left(\mathbb{R}^d\right)$
, and define the shift operator as
$A,B\in\mathscr{B}\!\left(\mathbb{R}^d\right)$
, and define the shift operator as
![]() $\Xi^x({\cdot}\times D)\,:\!=\,\Xi(({\cdot}+x)\times D)$
for all
$\Xi^x({\cdot}\times D)\,:\!=\,\Xi(({\cdot}+x)\times D)$
for all
![]() $x\in \mathbb{R}^d$
,
$x\in \mathbb{R}^d$
,
![]() $D\in \mathscr{T}$
.
$D\in \mathscr{T}$
.
Unrestricted case. See also [Reference Penrose and Yukich38].
Definition 2.3. The score function
![]() $\eta$
is translation-invariant if for all locally finite configurations
$\eta$
is translation-invariant if for all locally finite configurations
![]() $\mathscr{X}$
,
$\mathscr{X}$
,
![]() $x,y\in \mathbb{R}^d$
, and
$x,y\in \mathbb{R}^d$
, and
![]() $m\in T$
,
$m\in T$
,
![]() $\eta((x+y,m),\mathscr{X}\,)=\eta((x,m),\mathscr{X}^{\,y})$
.
$\eta((x+y,m),\mathscr{X}\,)=\eta((x,m),\mathscr{X}^{\,y})$
.
Restricted case. A translation may send a configuration outside of
![]() $\Gamma_\alpha$
, resulting in a completely different configuration inside
$\Gamma_\alpha$
, resulting in a completely different configuration inside
![]() $\Gamma_\alpha$
. For example, for a configuration
$\Gamma_\alpha$
. For example, for a configuration
![]() $\mathscr{X}\subset\Gamma_{\alpha}\times T$
and a point
$\mathscr{X}\subset\Gamma_{\alpha}\times T$
and a point
![]() $x\neq\textbf{0}$
in
$x\neq\textbf{0}$
in
![]() $\mathbb{R}^d$
, the translation
$\mathbb{R}^d$
, the translation
![]() $\mathscr{X}^x$
may not be a configuration contained in
$\mathscr{X}^x$
may not be a configuration contained in
![]() $\Gamma_{\alpha}\times T$
. To focus on the part that affects the score function, we expect the score function to take the same value for two configurations if the parts within their stabilising radii are completely inside
$\Gamma_{\alpha}\times T$
. To focus on the part that affects the score function, we expect the score function to take the same value for two configurations if the parts within their stabilising radii are completely inside
![]() $\Gamma_\alpha$
, and one is a translation of the other. More precisely, we have the following definition.
$\Gamma_\alpha$
, and one is a translation of the other. More precisely, we have the following definition.
Definition 2.4. A stabilising score function is called translation-invariant if for any
![]() $\alpha>0$
,
$\alpha>0$
,
![]() $x\in\Gamma_\alpha$
, and
$x\in\Gamma_\alpha$
, and
![]() $\mathscr{X}\in \boldsymbol{C}_{\mathbb{R}^d\times T}$
such that
$\mathscr{X}\in \boldsymbol{C}_{\mathbb{R}^d\times T}$
such that
![]() $\bar{R}(x,m,\alpha,\mathscr{X}\,)\le d(x,\partial\Gamma_\alpha)$
, where
$\bar{R}(x,m,\alpha,\mathscr{X}\,)\le d(x,\partial\Gamma_\alpha)$
, where
![]() $\partial A$
stands for the boundary of A, we have
$\partial A$
stands for the boundary of A, we have
![]() $\eta\!\left((x,m),\mathscr{X},\Gamma_\alpha\right)=\eta\!\left((x^{\prime},m),\mathscr{X}^{\,\prime},\Gamma_{\alpha^{\prime}}\right)$
and
$\eta\!\left((x,m),\mathscr{X},\Gamma_\alpha\right)=\eta\!\left((x^{\prime},m),\mathscr{X}^{\,\prime},\Gamma_{\alpha^{\prime}}\right)$
and
![]() $\bar{R}(x^{\prime},m,\alpha^{\prime},\mathscr{X}^{\,\prime})=\bar{R}(x,m,\alpha,\mathscr{X}\,)$
for all
$\bar{R}(x^{\prime},m,\alpha^{\prime},\mathscr{X}^{\,\prime})=\bar{R}(x,m,\alpha,\mathscr{X}\,)$
for all
![]() $\alpha^{\prime}>0$
,
$\alpha^{\prime}>0$
,
![]() $x^{\prime}\in\Gamma_{\alpha^{\prime}}$
, and
$x^{\prime}\in\Gamma_{\alpha^{\prime}}$
, and
![]() $\mathscr{X}^{\,\prime}\in \boldsymbol{C}_{\mathbb{R}^d\times T}$
such that
$\mathscr{X}^{\,\prime}\in \boldsymbol{C}_{\mathbb{R}^d\times T}$
such that
![]() $\bar{R}(x,m,\alpha,\mathscr{X}\,)\le d(x^{\prime},\partial\Gamma_{\alpha^{\prime}})$
and
$\bar{R}(x,m,\alpha,\mathscr{X}\,)\le d(x^{\prime},\partial\Gamma_{\alpha^{\prime}})$
and
Note that there is a tacit assumption of consistency in Definition 2.4, which implies that if
![]() $\eta$
is translation-invariant under Definition 2.4, then there exists a
$\eta$
is translation-invariant under Definition 2.4, then there exists a
![]() $\bar{g}\,:\, \boldsymbol{C}_{\mathbb{R}^d\times T}\rightarrow \mathbb{R}$
such that
$\bar{g}\,:\, \boldsymbol{C}_{\mathbb{R}^d\times T}\rightarrow \mathbb{R}$
such that
for
![]() $\mathscr{L}_{T}$
-almost-sure
$\mathscr{L}_{T}$
-almost-sure
![]() $m\in T$
and almost all realisations
$m\in T$
and almost all realisations
![]() $\mathscr{X}$
of the marked homogeneous Poisson point process
$\mathscr{X}$
of the marked homogeneous Poisson point process
![]() $\Xi\sim\mathscr{P}_{\lambda,\mathscr{L}_T}$
. Furthermore, we can see that for each score function
$\Xi\sim\mathscr{P}_{\lambda,\mathscr{L}_T}$
. Furthermore, we can see that for each score function
![]() $\eta$
satisfying the translation-invariance in Definition 2.4, there exists a score function for the unrestricted case, obtained by setting
$\eta$
satisfying the translation-invariance in Definition 2.4, there exists a score function for the unrestricted case, obtained by setting
and using its corresponding radius of stabilisation in the sense of Definition 2.1 as R. From the construction,
![]() $\bar{\eta}$
is range-bounded (resp. exponentially stabilising, polynomially stabilising of order
$\bar{\eta}$
is range-bounded (resp. exponentially stabilising, polynomially stabilising of order
![]() $\beta>0$
) in the sense of Definition 2.1 if
$\beta>0$
) in the sense of Definition 2.1 if
![]() $\eta$
is range-bounded (resp. exponentially stabilising, polynomially stabilising of order
$\eta$
is range-bounded (resp. exponentially stabilising, polynomially stabilising of order
![]() $\beta>0$
) in the sense of Definition 2.2. Moreover, if
$\beta>0$
) in the sense of Definition 2.2. Moreover, if
![]() $B(x, R(x)) \subset \Gamma_\alpha$
, then
$B(x, R(x)) \subset \Gamma_\alpha$
, then
![]() $\bar{R}(x, \alpha)= R(x)$
, and if
$\bar{R}(x, \alpha)= R(x)$
, and if
![]() $B(x, R(x)) \not\subset \Gamma_\alpha$
, then
$B(x, R(x)) \not\subset \Gamma_\alpha$
, then
![]() $\bar{R}(x,\alpha)>d\big(x,\partial \Gamma_\alpha\big)$
, but there is no definite relationship between
$\bar{R}(x,\alpha)>d\big(x,\partial \Gamma_\alpha\big)$
, but there is no definite relationship between
![]() $\bar{R}$
and R.
$\bar{R}$
and R.
Assumption 2.3. Moment condition
Unrestricted case. A score function
![]() $\eta$
is said to satisfy the kth moment condition if
$\eta$
is said to satisfy the kth moment condition if
for some positive constant C for all
![]() $a_i\in \{0,1\}$
, distinct
$a_i\in \{0,1\}$
, distinct
![]() $x_i\in \mathbb{R}^d$
,
$x_i\in \mathbb{R}^d$
,
![]() $i\in\{1,2\}$
, and i.i.d. random elements
$i\in\{1,2\}$
, and i.i.d. random elements
![]() $M_1$
,
$M_1$
,
![]() $M_2$
,
$M_2$
,
![]() $M_3\sim\mathscr{L}_{T}$
that are independent of
$M_3\sim\mathscr{L}_{T}$
that are independent of
![]() $\Xi$
.
$\Xi$
.
Restricted case. A score function
![]() $\eta$
is said to satisfy the kth moment condition if there exists a positive constant C independent of
$\eta$
is said to satisfy the kth moment condition if there exists a positive constant C independent of
![]() $\alpha$
such that
$\alpha$
such that
for all
![]() $a_1,a_2\in \{0,1\}$
, distinct
$a_1,a_2\in \{0,1\}$
, distinct
![]() $x_1,x_2,x_3\in \Gamma_\alpha$
, and i.i.d. random elements
$x_1,x_2,x_3\in \Gamma_\alpha$
, and i.i.d. random elements
![]() $M_1$
,
$M_1$
,
![]() $M_2$
,
$M_2$
,
![]() $M_3\sim\mathscr{L}_{T}$
that are independent of
$M_3\sim\mathscr{L}_{T}$
that are independent of
![]() $\Xi$
. From the construction, if
$\Xi$
. From the construction, if
![]() $\eta$
is stabilising, then
$\eta$
is stabilising, then
![]() $\bar{\eta}$
satisfies the moment condition of the same order in the sense of (2.3).
$\bar{\eta}$
satisfies the moment condition of the same order in the sense of (2.3).
Assumption 2.4. Non-singularity
Unrestricted case. The score function is said to be non-singular if
 \begin{equation} \mathscr{L}\!\left(\left.\sum_{(x,m)\in \Xi}\eta\!\left((x, m),\Xi\right)\textbf{1}_{d(x, N_0)<R(x)}\right|\sigma\Big(\Xi_{N_0^c}\Big)\right)\end{equation}
\begin{equation} \mathscr{L}\!\left(\left.\sum_{(x,m)\in \Xi}\eta\!\left((x, m),\Xi\right)\textbf{1}_{d(x, N_0)<R(x)}\right|\sigma\Big(\Xi_{N_0^c}\Big)\right)\end{equation}
has a positive probability of being non-singular for some bounded set
![]() $N_0$
. That is, the sum of the values of the score function affected by the points in
$N_0$
. That is, the sum of the values of the score function affected by the points in
![]() $N_0$
is non-singular.
$N_0$
is non-singular.
Restricted case. We define non-singularity when the score function is stabilising and translation-invariant. The score function
![]() $\eta$
for restricted input is said to be non-singular if it is stabilising, and the corresponding
$\eta$
for restricted input is said to be non-singular if it is stabilising, and the corresponding
![]() $\bar{\eta}$
defined in (2.2) satisfies that
$\bar{\eta}$
defined in (2.2) satisfies that
 \begin{equation} \mathscr{L}\!\left(\left.\sum_{(x,m)\in \Xi}\bar{\eta}\!\left((x, m),\Xi\right)\textbf{1}_{d(x, N_0)<R(x)}\right|\sigma\Big(\Xi_{N_0^c}\Big)\right) \end{equation}
\begin{equation} \mathscr{L}\!\left(\left.\sum_{(x,m)\in \Xi}\bar{\eta}\!\left((x, m),\Xi\right)\textbf{1}_{d(x, N_0)<R(x)}\right|\sigma\Big(\Xi_{N_0^c}\Big)\right) \end{equation}
has a positive probability of being non-singular for some bounded set
![]() $N_0$
.
$N_0$
.
The non-singularity assumptions above are stronger than the non-degeneracy conditions (1.10) and (1.12) in [Reference Xia and Yukich51] for Poisson input. The latter is comparable to the non-degeneracy condition in [Reference Penrose and Yukich38, Theorem 2.1]; see the proof of Lemma 5.9.
The main result for
![]() $W_\alpha$
(the unrestricted case) is summarised below.
$W_\alpha$
(the unrestricted case) is summarised below.
Theorem 2.1.
Let
![]() $Z_\alpha\sim N(\mathbb{E} W_{\alpha}, {\textrm{Var}}(W_{\alpha}))$
. Assume that the score function
$Z_\alpha\sim N(\mathbb{E} W_{\alpha}, {\textrm{Var}}(W_{\alpha}))$
. Assume that the score function
![]() $\eta$
is translation-invariant as in Definition 2.2 and satisfies the non-singularity in Assumption 2.4.
$\eta$
is translation-invariant as in Definition 2.2 and satisfies the non-singularity in Assumption 2.4.
-
(i) If
 $\eta$
is range-bounded as in Definition 2.1 and satisfies the third moment condition (2.3), then
$\eta$
is range-bounded as in Definition 2.1 and satisfies the third moment condition (2.3), then  \begin{equation*}d_{TV}(W_\alpha,Z_\alpha)\le \mathop{{}\textrm{O}}\mathopen{}\left(\alpha^{-\frac{1}{2}}\right).\end{equation*}
\begin{equation*}d_{TV}(W_\alpha,Z_\alpha)\le \mathop{{}\textrm{O}}\mathopen{}\left(\alpha^{-\frac{1}{2}}\right).\end{equation*}
-
(ii) If
 $\eta$
is exponentially stabilising as in Definition 2.1 and satisfies the third moment condition (2.3), then
$\eta$
is exponentially stabilising as in Definition 2.1 and satisfies the third moment condition (2.3), then  \begin{equation*}d_{TV}(W_\alpha,Z_\alpha)\le \mathop{{}\textrm{O}}\mathopen{}\left(\alpha^{-\frac{1}{2}}\ln\!(\alpha)^{\frac{5d}{2}}\right).\end{equation*}
\begin{equation*}d_{TV}(W_\alpha,Z_\alpha)\le \mathop{{}\textrm{O}}\mathopen{}\left(\alpha^{-\frac{1}{2}}\ln\!(\alpha)^{\frac{5d}{2}}\right).\end{equation*}
-
(iii) If
 $\eta$
is polynomially stabilising as in Definition 2.1 with parameter
$\eta$
is polynomially stabilising as in Definition 2.1 with parameter
 $\beta>\frac{(15k-14)d}{k-2}$
and satisfies the k′th moment condition (2.3) with
$\beta>\frac{(15k-14)d}{k-2}$
and satisfies the k′th moment condition (2.3) with
 $k^{\prime}>k\ge 3$
, then
$k^{\prime}>k\ge 3$
, then  \begin{align*} d_{TV}\!\left(W_\alpha,Z_\alpha\right)&\le \mathop{{}\textrm{O}}\mathopen{}\left(\alpha^{-\frac{\beta(k-2)[\beta(k-2)-d(15k-14)]}{(k\beta-2\beta-dk)(5dk+2\beta k-4\beta)}}\right). \end{align*}
\begin{align*} d_{TV}\!\left(W_\alpha,Z_\alpha\right)&\le \mathop{{}\textrm{O}}\mathopen{}\left(\alpha^{-\frac{\beta(k-2)[\beta(k-2)-d(15k-14)]}{(k\beta-2\beta-dk)(5dk+2\beta k-4\beta)}}\right). \end{align*}
When approximation error is measured in terms of the Kolmogorov distance, the distributions of
![]() $W_\alpha$
and
$W_\alpha$
and
![]() $\bar{W}_\alpha$
are often close for large
$\bar{W}_\alpha$
are often close for large
![]() $\alpha$
. However, in terms of the total variation distance, one cannot infer the accuracy of the normal approximation of
$\alpha$
. However, in terms of the total variation distance, one cannot infer the accuracy of the normal approximation of
![]() $W_\alpha$
by taking the limit of that of
$W_\alpha$
by taking the limit of that of
![]() $\bar{W}_\alpha$
. For this reason, we need to adapt the conditions accordingly and tackle
$\bar{W}_\alpha$
. For this reason, we need to adapt the conditions accordingly and tackle
![]() $\bar{W}_\alpha$
separately. We state the main result for
$\bar{W}_\alpha$
separately. We state the main result for
![]() $\bar{W}_\alpha$
(the restricted case) in the following theorem.
$\bar{W}_\alpha$
(the restricted case) in the following theorem.
Theorem 2.2.
Let
![]() $\bar{Z}_\alpha\sim N(\mathbb{E}\bar{W}_\alpha,{\textrm{Var}}(\bar{W}_\alpha))$
. Assume that
$\bar{Z}_\alpha\sim N(\mathbb{E}\bar{W}_\alpha,{\textrm{Var}}(\bar{W}_\alpha))$
. Assume that
![]() $\eta$
is translation-invariant as in Definition 2.4 and satisfies the non-singularity in Assumption 2.4.
$\eta$
is translation-invariant as in Definition 2.4 and satisfies the non-singularity in Assumption 2.4.
-
(i) If
 $\eta$
is range-bounded as in Definition 2.2 and satisfies the third moment condition (2.4), then
$\eta$
is range-bounded as in Definition 2.2 and satisfies the third moment condition (2.4), then  \begin{equation*}d_{TV}(\bar{W}_\alpha,\bar{Z}_\alpha)\le \mathop{{}\textrm{O}}\mathopen{}\left(\alpha^{-\frac{1}{2}}\right).\end{equation*}
\begin{equation*}d_{TV}(\bar{W}_\alpha,\bar{Z}_\alpha)\le \mathop{{}\textrm{O}}\mathopen{}\left(\alpha^{-\frac{1}{2}}\right).\end{equation*}
-
(ii) If
 $\eta$
is exponentially stabilising as in Definition 2.2 and satisfies the third moment condition (2.4), then
$\eta$
is exponentially stabilising as in Definition 2.2 and satisfies the third moment condition (2.4), then  \begin{equation*}d_{TV}(\bar{W}_\alpha,\bar{Z}_\alpha)\le \mathop{{}\textrm{O}}\mathopen{}\left(\alpha^{-\frac{1}{2}}\ln\!(\alpha)^{\frac{5d}{2}}\right).\end{equation*}
\begin{equation*}d_{TV}(\bar{W}_\alpha,\bar{Z}_\alpha)\le \mathop{{}\textrm{O}}\mathopen{}\left(\alpha^{-\frac{1}{2}}\ln\!(\alpha)^{\frac{5d}{2}}\right).\end{equation*}
-
(iii) If
 $\eta$
is polynomially stabilising as in Definition 2.2 with parameter
$\eta$
is polynomially stabilising as in Definition 2.2 with parameter
 $\beta>\frac{(15k-14)d}{k-2}$
and satisfies the k′th moment condition (2.4) with
$\beta>\frac{(15k-14)d}{k-2}$
and satisfies the k′th moment condition (2.4) with
 $k^{\prime}>k\ge 3$
, then
$k^{\prime}>k\ge 3$
, then  \begin{equation*}d_{TV}\!\left(\bar{W}_\alpha,\bar{Z}_\alpha\right)\le \mathop{{}\textrm{O}}\mathopen{}\left(\alpha^{-\frac{\beta(k-2)[\beta(k-2)-d(15k-14)]}{(k\beta-2\beta-dk)(5dk+2\beta k-4\beta)}}\right). \end{equation*}
\begin{equation*}d_{TV}\!\left(\bar{W}_\alpha,\bar{Z}_\alpha\right)\le \mathop{{}\textrm{O}}\mathopen{}\left(\alpha^{-\frac{\beta(k-2)[\beta(k-2)-d(15k-14)]}{(k\beta-2\beta-dk)(5dk+2\beta k-4\beta)}}\right). \end{equation*}
3. Applications
Our main result can be applied to a wide range of geometric probability problems, including the normal approximation of functionals of k-nearest-neighbours graphs, Voronoi graphs, sphere-of-influence graphs, Delaunay triangulation graphs, Gabriel graphs, and relative neighbourhood graphs. To keep our article to a reasonable length, we give details only for the k-nearest-neighbours graph and the Voronoi graph. We can see that many functionals of the graphs, such as the total edge length, satisfy the conditions of the main theorems naturally, and the ideas for verifying these conditions are similar. For ease of reading, we briefly introduce these graphs below; more details can be found in [Reference Devroye17, Reference Toussaint48].
Let
![]() $\mathscr{X}\subset {\mathbb{R}^d}$
be a locally finite point set.
$\mathscr{X}\subset {\mathbb{R}^d}$
be a locally finite point set.
-
(i) The k-nearest-neighbours graph. The k-nearest-neighbours graph
 $NG(\mathscr{X}\,)$
is the graph obtained by including
$NG(\mathscr{X}\,)$
is the graph obtained by including
 $\{x,y\}$
as an edge whenever y is one of the k points nearest to x or x is one of the k points nearest to y. A variant of
$\{x,y\}$
as an edge whenever y is one of the k points nearest to x or x is one of the k points nearest to y. A variant of
 $NG(\mathscr{X}\,)$
considered in the literature is the directed graph
$NG(\mathscr{X}\,)$
considered in the literature is the directed graph
 $NG^{\prime}\left(\mathscr{X}\right)$
, which is constructed by inserting a directed edge (x, y) if y is one of the k nearest neighbours of x.
$NG^{\prime}\left(\mathscr{X}\right)$
, which is constructed by inserting a directed edge (x, y) if y is one of the k nearest neighbours of x. -
(ii) Voronoi tessellations. We enumerate the points in
 $\mathscr{X}$
as
$\mathscr{X}$
as
 $\{x_1,x_2,\dots\}$
, and for each
$\{x_1,x_2,\dots\}$
, and for each
 $i \in \mathbb{N}$
we denote by
$i \in \mathbb{N}$
we denote by
 $C(x_i)\,:\!=\,C(x_i,\mathscr{X}\,)$
the locus of points in
$C(x_i)\,:\!=\,C(x_i,\mathscr{X}\,)$
the locus of points in
 $\mathbb{R}^d$
closer to
$\mathbb{R}^d$
closer to
 $x_i$
than to any other points in
$x_i$
than to any other points in
 $\mathscr{X}$
. We can see that
$\mathscr{X}$
. We can see that
 $C(x_i)$
is the intersection of half-planes. In particular, when the point set
$C(x_i)$
is the intersection of half-planes. In particular, when the point set
 $\mathscr{X}$
has
$\mathscr{X}$
has
 $n<\infty$
points,
$n<\infty$
points,
 $C(x_i)$
is a convex polygonal region with at most
$C(x_i)$
is a convex polygonal region with at most
 $n-1$
sides,
$n-1$
sides,
 $1\le i\le n$
. The cells
$1\le i\le n$
. The cells
 $C(x_i)$
form a partition of
$C(x_i)$
form a partition of
 $\mathbb{R}^d$
. The partition is called a Voronoi tessellation, and the points in
$\mathbb{R}^d$
. The partition is called a Voronoi tessellation, and the points in
 $\mathscr{X}$
are usually called Voronoi generators.
$\mathscr{X}$
are usually called Voronoi generators. -
(iii) The Delaunay triangulation graph. The Delaunay triangulation graph puts an edge between two points in
 $\mathscr{X}$
if these points are centres of adjacent Voronoi cells; it is a dual of a Voronoi tessellation.
$\mathscr{X}$
if these points are centres of adjacent Voronoi cells; it is a dual of a Voronoi tessellation. -
(iv) The Gabriel graph. The Gabriel graph puts an edge between two points x and y in
 $\mathscr{X}$
if the ball centred at the middle point
$\mathscr{X}$
if the ball centred at the middle point
 $\frac{x+y}{2}$
with radius
$\frac{x+y}{2}$
with radius
 $\big\|\frac{x-y}{2}\big\|$
does not contain any other points in
$\big\|\frac{x-y}{2}\big\|$
does not contain any other points in
 $\mathscr{X}$
. We can see that the Gabriel graph is a subgraph of the Delaunay triangulation graph.
$\mathscr{X}$
. We can see that the Gabriel graph is a subgraph of the Delaunay triangulation graph. -
(v) The relative neighbourhood graph. The relative neighbourhood graph puts an edge between two points x and y in
 $\mathscr{X}$
if
$\mathscr{X}$
if
 $B(x,\|x-y\|)\cap B(y,\|x-y\|)\cap\mathscr{X} =\emptyset$
. When
$B(x,\|x-y\|)\cap B(y,\|x-y\|)\cap\mathscr{X} =\emptyset$
. When
 $d=2$
, this means that the vesica piscis between x and y does not contain any other points in
$d=2$
, this means that the vesica piscis between x and y does not contain any other points in
 $\mathscr{X}$
. This graph is a subgraph of Gabriel graph, so it is also a subgraph of Delaunay triangulation graph.
$\mathscr{X}$
. This graph is a subgraph of Gabriel graph, so it is also a subgraph of Delaunay triangulation graph. -
(vi) The sphere-of-influence graph. The sphere-of-influence graph of a locally finite point set
 $\mathscr{X}\subset {\mathbb{R}^d}$
is the graph obtained by including
$\mathscr{X}\subset {\mathbb{R}^d}$
is the graph obtained by including
 $\{x,y\}$
as an edge whenever
$\{x,y\}$
as an edge whenever
 $x,y\in\mathscr{X}$
and
$x,y\in\mathscr{X}$
and
 $\|x-y\|\le \|x-N(x,\mathscr{X}\,)\|+\|y-N(y, \mathscr{X}\,)\|$
, where for
$\|x-y\|\le \|x-N(x,\mathscr{X}\,)\|+\|y-N(y, \mathscr{X}\,)\|$
, where for
 $z\in\mathscr{X}$
,
$z\in\mathscr{X}$
,
 $N(z,\mathscr{X}\,)$
is the nearest point to z in
$N(z,\mathscr{X}\,)$
is the nearest point to z in
 $\mathscr{X}$
. That is, for every point
$\mathscr{X}$
. That is, for every point
 $z\in \mathscr{X}$
, we draw a circle with centre z whose radius is the distance between z and the point nearest to it in
$z\in \mathscr{X}$
, we draw a circle with centre z whose radius is the distance between z and the point nearest to it in
 $\mathscr{X}$
; then two points x, y are connected if the circles centred at x and y intersect.
$\mathscr{X}$
; then two points x, y are connected if the circles centred at x and y intersect.
Remark 3.1. Using [Reference Lachièze-Rey, Schulte and Yukich30, Corollary 2.2] or [Reference Chen, Röllin and Xia13, Theorem 3.1], it is possible to consider normal approximation to the statistics in Section 3.1 and Section 3.2 under the Kolmogorov distance with convergence rate
![]() $\mathop{{}\textrm{O}}\mathopen{}\big(\alpha^{-\frac{1}{2}}\big)$
instead of
$\mathop{{}\textrm{O}}\mathopen{}\big(\alpha^{-\frac{1}{2}}\big)$
instead of
![]() $\mathop{{}\textrm{O}}\mathopen{}\left(\alpha^{-\frac{1}{2}}\ln\!(\alpha)^{\frac{5d}{2}}\right)$
.
$\mathop{{}\textrm{O}}\mathopen{}\left(\alpha^{-\frac{1}{2}}\ln\!(\alpha)^{\frac{5d}{2}}\right)$
.
3.1. The total edge length of the k-nearest-neighbours graph
Theorem 3.1.
If
![]() $\Xi$
is a homogeneous Poisson point process, then the total edge length
$\Xi$
is a homogeneous Poisson point process, then the total edge length
![]() $\bar{W}_\alpha$
$\bar{W}_\alpha$
![]() $\big($
resp.
$\big($
resp.
![]() $\bar{W}^{\prime}_\alpha\big)$
of
$\bar{W}^{\prime}_\alpha\big)$
of
![]() $NG\!\left(\Xi_{\Gamma_{\alpha}}\right)$
$NG\!\left(\Xi_{\Gamma_{\alpha}}\right)$
![]() $\Big($
resp.
$\Big($
resp.
![]() $NG^{\prime}\left(\Xi_{\Gamma_{\alpha}}\right)\Big)$
satisfies
$NG^{\prime}\left(\Xi_{\Gamma_{\alpha}}\right)\Big)$
satisfies
where
![]() ${\bar{Z}}_\alpha$
${\bar{Z}}_\alpha$
![]() $\big($
resp.
$\big($
resp.
![]() ${\bar{Z}}^{\prime}_\alpha\big)$
is a normal random variable with the same mean and variance as
${\bar{Z}}^{\prime}_\alpha\big)$
is a normal random variable with the same mean and variance as
![]() $\bar{W}_\alpha$
$\bar{W}_\alpha$
![]() $\big($
resp.
$\big($
resp.
![]() $\bar{W}^{\prime}_\alpha\big)$
.
$\bar{W}^{\prime}_\alpha\big)$
.
Proof. We adapt the idea of the proof in [Reference Penrose and Yukich38] to our setup. We only show the claim for the total edge length of
![]() $NG\!\left(\Xi_{\Gamma_{\alpha}}\right)$
since
$NG\!\left(\Xi_{\Gamma_{\alpha}}\right)$
since
![]() $NG^{\prime}\left(\Xi_{\Gamma_{\alpha}}\right)$
can be handled with the same idea. The score function in this case is
$NG^{\prime}\left(\Xi_{\Gamma_{\alpha}}\right)$
can be handled with the same idea. The score function in this case is
which is clearly translation-invariant.
To apply Theorem 2.2, we need to check the moment condition (2.4), the non-singularity in Assumption 2.4, and the stabilisation condition in Definition 2.2. For simplicity, we show these conditions in two-dimensional cases; the argument can easily be extended to
![]() $\mathbb{R}^d$
with
$\mathbb{R}^d$
with
![]() $d\ge 3$
(resp.
$d\ge 3$
(resp.
![]() $d=1$
) by using cones (resp. intervals) instead of triangles in the proof.
$d=1$
) by using cones (resp. intervals) instead of triangles in the proof.
We start with the exponential stabilisation, and fix
![]() $\alpha>0$
and
$\alpha>0$
and
![]() $x\in \Gamma_\alpha$
. Referring to Figure 3, for each
$x\in \Gamma_\alpha$
. Referring to Figure 3, for each
![]() $t>0$
, we construct six disjoint sectors of the same size
$t>0$
, we construct six disjoint sectors of the same size
![]() $T_j(t)$
,
$T_j(t)$
,
![]() $1\le j\le 6$
, with x as the centre and angle
$1\le j\le 6$
, with x as the centre and angle
![]() $\frac{\pi}{3}$
. In consideration of edge effects near the boundary of
$\frac{\pi}{3}$
. In consideration of edge effects near the boundary of
![]() $\Gamma_\alpha$
, the sectors are rotated around x so that all straight edges of the sectors have angles at least
$\Gamma_\alpha$
, the sectors are rotated around x so that all straight edges of the sectors have angles at least
![]() $\pi/12$
with respect to the edges of
$\pi/12$
with respect to the edges of
![]() $\Gamma_\alpha$
. It is clear that
$\Gamma_\alpha$
. It is clear that
![]() $T_j(t)\subset T_j(u)$
for all
$T_j(t)\subset T_j(u)$
for all
![]() $0<t<u$
. Set
$0<t<u$
. Set
![]() $T_{j}(\infty)=\cup_{t>0}T_j(t)$
for
$T_{j}(\infty)=\cup_{t>0}T_j(t)$
for
![]() $1\le j\le 6$
; then from the properties of the Poisson point process, there are infinitely many points in
$1\le j\le 6$
; then from the properties of the Poisson point process, there are infinitely many points in
![]() $\Xi\cap T_{j}(\infty)$
for all j, a.s. Let
$\Xi\cap T_{j}(\infty)$
for all j, a.s. Let
![]() $|A|$
denote the cardinality of the set A; define
$|A|$
denote the cardinality of the set A; define
and
![]() $\bar{R}\!\left(x,\alpha\right)=3t_{x,\alpha}$
. We show that
$\bar{R}\!\left(x,\alpha\right)=3t_{x,\alpha}$
. We show that
![]() $\bar{R}$
is a radius of stabilisation, and its tail distribution can be bounded by an exponentially decaying function independent of
$\bar{R}$
is a radius of stabilisation, and its tail distribution can be bounded by an exponentially decaying function independent of
![]() $\alpha$
and x.
$\alpha$
and x.

Figure 3. k-nearest: stabilisation.
For the radius of stabilisation, there are two cases to consider. The first case is that none of
![]() $T_j(t_{x,\alpha})\cap \Gamma_\alpha\cap\Xi$
,
$T_j(t_{x,\alpha})\cap \Gamma_\alpha\cap\Xi$
,
![]() $1\le j\le 6$
, contains at least
$1\le j\le 6$
, contains at least
![]() $k+1$
points; then
$k+1$
points; then
![]() $B\big(x, \bar{R}\big(x,\alpha\big)\big)\supset \Gamma_\alpha$
, and (2.1) is obvious. The second case is that at least one of
$B\big(x, \bar{R}\big(x,\alpha\big)\big)\supset \Gamma_\alpha$
, and (2.1) is obvious. The second case is that at least one of
![]() $T_j(t_{x,\alpha})\cap \Gamma_\alpha\cap\Xi$
,
$T_j(t_{x,\alpha})\cap \Gamma_\alpha\cap\Xi$
,
![]() $1\le j\le 6$
, contains at least
$1\le j\le 6$
, contains at least
![]() $k+1$
points, which means that the k nearest neighbours
$k+1$
points, which means that the k nearest neighbours
![]() $\{x_1,\dots,x_k\}$
of x are in
$\{x_1,\dots,x_k\}$
of x are in
![]() $B\!\left(x,t_{x,\alpha}\right)$
. If a point
$B\!\left(x,t_{x,\alpha}\right)$
. If a point
![]() $y\in \Gamma_\alpha\backslash B(x,t_{x,\alpha})$
, then
$y\in \Gamma_\alpha\backslash B(x,t_{x,\alpha})$
, then
![]() $y\in \Gamma_\alpha\cap (T_j(\infty)\backslash T_j(t_{x,\alpha}))$
for some j. Since
$y\in \Gamma_\alpha\cap (T_j(\infty)\backslash T_j(t_{x,\alpha}))$
for some j. Since
![]() $\Gamma_\alpha\cap (T_j(\infty)\backslash T_j(t_{x,\alpha}))$
is non-empty,
$\Gamma_\alpha\cap (T_j(\infty)\backslash T_j(t_{x,\alpha}))$
is non-empty,
![]() $T_j(t_{x,\alpha})$
contains at least
$T_j(t_{x,\alpha})$
contains at least
![]() $k+1$
points
$k+1$
points
![]() $\{y_1,\dots, y_{k+1}\}$
and
$\{y_1,\dots, y_{k+1}\}$
and
![]() $d(x,y)>d(y_i,y)$
for all
$d(x,y)>d(y_i,y)$
for all
![]() $i\le k+1$
; hence y cannot have x as one of its k nearest neighbours. This ensures that all points having x as one of their k nearest neighbours are in
$i\le k+1$
; hence y cannot have x as one of its k nearest neighbours. This ensures that all points having x as one of their k nearest neighbours are in
![]() $B(x, t_{x,\alpha})$
. Noting that the diameter of
$B(x, t_{x,\alpha})$
. Noting that the diameter of
![]() $B\!\left(x,t_{x,\alpha}\right)$
is
$B\!\left(x,t_{x,\alpha}\right)$
is
![]() $2t_{x,\alpha}$
and there are at least
$2t_{x,\alpha}$
and there are at least
![]() $k+1$
points in
$k+1$
points in
![]() $B\!\left(x,t_{x,\alpha}\right)$
, we can see that whether a point y in
$B\!\left(x,t_{x,\alpha}\right)$
, we can see that whether a point y in
![]() $B\!\left(x,t_{x,\alpha}\right)$
has x as one of its k nearest neighbours is entirely determined by
$B\!\left(x,t_{x,\alpha}\right)$
has x as one of its k nearest neighbours is entirely determined by
![]() $\Xi\cap B(y,2t_{x,\alpha})\subset \Xi\cap B(x,3t_{x,\alpha})$
. This guarantees that
$\Xi\cap B(y,2t_{x,\alpha})\subset \Xi\cap B(x,3t_{x,\alpha})$
. This guarantees that
![]() $\eta\!\left(x,\mathscr{X},\Gamma_\alpha\right)$
is
$\eta\!\left(x,\mathscr{X},\Gamma_\alpha\right)$
is
![]() $\sigma\!\left(\Xi_{B(x,3t_{x,\alpha})}\right)$
-measurable, and
$\sigma\!\left(\Xi_{B(x,3t_{x,\alpha})}\right)$
-measurable, and
![]() $\bar{R}\!\left(x,\alpha\right)$
is a radius of stabilisation. For the tail distribution of
$\bar{R}\!\left(x,\alpha\right)$
is a radius of stabilisation. For the tail distribution of
![]() $\bar{R}$
, referring to Figure 4, we consider the number of points of
$\bar{R}$
, referring to Figure 4, we consider the number of points of
![]() $\Xi$
falling into a triangle
$\Xi$
falling into a triangle
![]() $A_t$
as a result of a sector being chopped off by the edge of
$A_t$
as a result of a sector being chopped off by the edge of
![]() $\Gamma_\alpha$
. This is the worst situation for capturing the number of points by one sector intersecting
$\Gamma_\alpha$
. This is the worst situation for capturing the number of points by one sector intersecting
![]() $\Gamma_{\alpha}$
in the sense of volume. A routine trigonometry calculation gives that the area of
$\Gamma_{\alpha}$
in the sense of volume. A routine trigonometry calculation gives that the area of
![]() $A_t$
is at least
$A_t$
is at least
![]() $0.116t^2$
. Define
$0.116t^2$
. Define
![]() $\tau\,:\!=\,\inf\{t\,:\,|\Xi\cap A_t|\ge k+1\}$
; then
$\tau\,:\!=\,\inf\{t\,:\,|\Xi\cap A_t|\ge k+1\}$
; then
 \begin{equation}\mathbb{P}\!\left(\bar{R}\!\left(x,\alpha\right)>t\right)\le 6\mathbb{P}\!\left(\tau>t/3\right)\le 6e^{-0.116\lambda (t/3)^2}\sum_{i=0}^k\frac{\left(0.116\lambda (t/3)^2\right)^i}{i!},\ t>0,\end{equation}
\begin{equation}\mathbb{P}\!\left(\bar{R}\!\left(x,\alpha\right)>t\right)\le 6\mathbb{P}\!\left(\tau>t/3\right)\le 6e^{-0.116\lambda (t/3)^2}\sum_{i=0}^k\frac{\left(0.116\lambda (t/3)^2\right)^i}{i!},\ t>0,\end{equation}
which implies the exponential stabilisation.

Figure 4.
k-nearest:
![]() $A_t$
.
$A_t$
.
The non-singularity in Assumption 2.4 can be proved through the corresponding unrestricted score function
![]() $\bar{\eta}(x,\mathscr{X}\,)=\frac{1}{2}\sum_{y\in \mathscr{X}}\|y-x\|\textbf{1}_{\{(x,y)\in NG(\mathscr{X}\,)\}}.$
Referring to Figure 5, we take
$\bar{\eta}(x,\mathscr{X}\,)=\frac{1}{2}\sum_{y\in \mathscr{X}}\|y-x\|\textbf{1}_{\{(x,y)\in NG(\mathscr{X}\,)\}}.$
Referring to Figure 5, we take
![]() $N_0\,:\!=\,B(0,{0.5})$
, observe that
$N_0\,:\!=\,B(0,{0.5})$
, observe that
![]() $\partial B(0,6)$
can be covered by finitely many B(x, 3) with
$\partial B(0,6)$
can be covered by finitely many B(x, 3) with
![]() $\|x\|=5$
, and write the centres of these balls as
$\|x\|=5$
, and write the centres of these balls as
![]() $x_1$
,
$x_1$
,
![]() $\dots$
,
$\dots$
,
![]() $x_n$
(in the two-dimensional case,
$x_n$
(in the two-dimensional case,
![]() $n=5$
). Let E be the event that
$n=5$
). Let E be the event that
![]() $|B(x_i,1)\cap \Xi|\ge k+1$
for all
$|B(x_i,1)\cap \Xi|\ge k+1$
for all
![]() $1\le i\le n$
,
$1\le i\le n$
,
![]() $|\left(B(0,{1})\backslash B(0,{0.5})\right)\cap\Xi|=k$
, and
$|\left(B(0,{1})\backslash B(0,{0.5})\right)\cap\Xi|=k$
, and
![]() $\Xi\cap \left(B(0,6)\backslash \left(\cup_{i\le n}B(x_i,1)\cup B(0,{1})\right)\right)$
is empty; then E is
$\Xi\cap \left(B(0,6)\backslash \left(\cup_{i\le n}B(x_i,1)\cup B(0,{1})\right)\right)$
is empty; then E is
![]() $\sigma\Big(\Xi_{N_0^c}\Big)$
-measurable and
$\sigma\Big(\Xi_{N_0^c}\Big)$
-measurable and
![]() $\mathbb{P}(E)>0$
. Conditional on E, we can see that
$\mathbb{P}(E)>0$
. Conditional on E, we can see that
![]() $E_1\,:\!=\,\{|\Xi\cap B(0,{0.5})|=1\}$
satisfies
$E_1\,:\!=\,\{|\Xi\cap B(0,{0.5})|=1\}$
satisfies
![]() $\mathbb{P}(E_1|E)>0$
, and on
$\mathbb{P}(E_1|E)>0$
, and on
![]() $E_1$
, all of the summands in (2.6) that are random are those involving the point of
$E_1$
, all of the summands in (2.6) that are random are those involving the point of
![]() $\Xi_{B(0,{0.5})}$
; thus we now establish that these random score functions are entirely determined by
$\Xi_{B(0,{0.5})}$
; thus we now establish that these random score functions are entirely determined by
![]() $\Xi_{B(0,{1})}$
. As a matter of fact, any point in
$\Xi_{B(0,{1})}$
. As a matter of fact, any point in
![]() $\Xi\cap \left(\cup_{1\le i\le n}B(x_i,1)\right)$
has k nearest points with distances no larger than 2, so points in
$\Xi\cap \left(\cup_{1\le i\le n}B(x_i,1)\right)$
has k nearest points with distances no larger than 2, so points in
![]() $\Xi\cap B(0,{1})$
cannot be among the k nearest points to points in
$\Xi\cap B(0,{1})$
cannot be among the k nearest points to points in
![]() $\Xi\cap B(x_i,1)$
. For any point
$\Xi\cap B(x_i,1)$
. For any point
![]() $y\in \Xi\cap B(0,6)^c$
, the line between 0 and y intersects
$y\in \Xi\cap B(0,6)^c$
, the line between 0 and y intersects
![]() $\partial B(0,6)$
at y
′, which is in
$\partial B(0,6)$
at y
′, which is in
![]() $B(x_{i_0},3)$
for some
$B(x_{i_0},3)$
for some
![]() $1\le i_0\le n$
, so the distances between y and points in
$1\le i_0\le n$
, so the distances between y and points in
![]() $\Xi\cap B(x_{i_0},3)$
are at most
$\Xi\cap B(x_{i_0},3)$
are at most
![]() $\|y-y^{\prime}\|+4=\|y\|-2$
. The distances between y and points in
$\|y-y^{\prime}\|+4=\|y\|-2$
. The distances between y and points in
![]() $\Xi\cap B(0,{1})$
are at least
$\Xi\cap B(0,{1})$
are at least
![]() $\|y\|-1$
, which ensures that points of
$\|y\|-1$
, which ensures that points of
![]() $\Xi\cap B(0,6)^c$
cannot have points in
$\Xi\cap B(0,6)^c$
cannot have points in
![]() $\Xi\cap B(0,{1})$
as their k nearest neighbours. On the other hand, on
$\Xi\cap B(0,{1})$
as their k nearest neighbours. On the other hand, on
![]() $E\cap E_1$
, there are
$E\cap E_1$
, there are
![]() $k+1$
points in
$k+1$
points in
![]() $\Xi\cap B(0,1)$
. For any point
$\Xi\cap B(0,1)$
. For any point
![]() $x\in B(0,1)$
, since the distances between x and other points in B (0, 1) are less than 2, the points outside
$x\in B(0,1)$
, since the distances between x and other points in B (0, 1) are less than 2, the points outside
![]() $B(x,2)\subset B(0,3)$
will not be among the k nearest points to x:
$B(x,2)\subset B(0,3)$
will not be among the k nearest points to x:
Hence, given E, all random score functions contributing to the sum of (2.6) are those completely determined by
![]() $\Xi_{B(0,2)}$
, giving
$\Xi_{B(0,2)}$
, giving
where X is
![]() $\sigma\Big(\Xi_{N_0^c}\Big)$
-measurable. Since this is a continuous function of
$\sigma\Big(\Xi_{N_0^c}\Big)$
-measurable. Since this is a continuous function of
![]() $y\in \Xi\cap B(0,{0.5})$
, the non-singularity in Assumption 2.4 follows.
$y\in \Xi\cap B(0,{0.5})$
, the non-singularity in Assumption 2.4 follows.

Figure 5. k-nearest: non-singularity.
For the moment condition (2.4), recalling the definition of
![]() $t_{x,\alpha}$
in (3.1), we replace x with
$t_{x,\alpha}$
in (3.1), we replace x with
![]() $x_3$
to get
$x_3$
to get
![]() $t_{x_3,\alpha}$
. We now establish that
$t_{x_3,\alpha}$
. We now establish that
In fact, the k nearest neighbours to
![]() $x_3$
have the contribution of the total edge length
$x_3$
have the contribution of the total edge length
![]() $\le \frac12 kt_{x_3,\alpha}$
. On the other hand, for
$\le \frac12 kt_{x_3,\alpha}$
. On the other hand, for
![]() $1\le j\le 6$
, each point in
$1\le j\le 6$
, each point in
![]() $\left(\Xi_{\Gamma_{\alpha}}+a_1\delta_{x_1}+a_2\delta_{x_2}\right)\cap T_{j}\!\left(t_{x_3,\alpha}\right)$
may take
$\left(\Xi_{\Gamma_{\alpha}}+a_1\delta_{x_1}+a_2\delta_{x_2}\right)\cap T_{j}\!\left(t_{x_3,\alpha}\right)$
may take
![]() $x_3$
as its k nearest neighbour, with the contribution to the total edge length
$x_3$
as its k nearest neighbour, with the contribution to the total edge length
![]() $\le \frac12 t_{x_3,\alpha}$
. As there are six sectors
$\le \frac12 t_{x_3,\alpha}$
. As there are six sectors
![]() $\left(\Xi_{\Gamma_{\alpha}}+a_1\delta_{x_1}+a_2\delta_{x_2}\right)\cap T_{j}\!\left(t_{x_3,\alpha}\right)$
,
$\left(\Xi_{\Gamma_{\alpha}}+a_1\delta_{x_1}+a_2\delta_{x_2}\right)\cap T_{j}\!\left(t_{x_3,\alpha}\right)$
,
![]() $1\le j\le 6$
, and each sector has no more than k points, with
$1\le j\le 6$
, and each sector has no more than k points, with
![]() $x_3$
as one of their k nearest neighbours, the contribution to the total edge length from this part is bounded by
$x_3$
as one of their k nearest neighbours, the contribution to the total edge length from this part is bounded by
![]() $3kt_{x_3,\alpha}$
. By adding these two bounds, we obtain (3.3). Finally, we combine (3.3) and (3.2) to get
$3kt_{x_3,\alpha}$
. By adding these two bounds, we obtain (3.3). Finally, we combine (3.3) and (3.2) to get
and the proof is completed by applying Theorem 2.2.
3.2. The total edge length of a Voronoi tessellation
Consider a finite point set
![]() $\mathscr{X}\subset \Gamma_\alpha$
. The Voronoi tessellation in
$\mathscr{X}\subset \Gamma_\alpha$
. The Voronoi tessellation in
![]() $\Gamma_\alpha$
generated by
$\Gamma_\alpha$
generated by
![]() $\mathscr{X}$
is the partition formed by cells
$\mathscr{X}$
is the partition formed by cells
![]() $C(x_i,\mathscr{X}\,)\cap \Gamma_\alpha$
; see Figure 6. We write the graph of this tessellation as
$C(x_i,\mathscr{X}\,)\cap \Gamma_\alpha$
; see Figure 6. We write the graph of this tessellation as
![]() $V(\mathscr{X},\alpha)$
and the total edge length of
$V(\mathscr{X},\alpha)$
and the total edge length of
![]() $V(\mathscr{X},\alpha)$
as
$V(\mathscr{X},\alpha)$
as
![]() $\mathscr{V}(\mathscr{X},\alpha)$
.
$\mathscr{V}(\mathscr{X},\alpha)$
.

Figure 6. Voronoi tessellation.
Theorem 3.2.
If
![]() $\Xi$
is a homogeneous Poisson point process, then
$\Xi$
is a homogeneous Poisson point process, then
where
![]() ${\bar{Z}}_\alpha$
is a normal random variable with the same mean and variance as
${\bar{Z}}_\alpha$
is a normal random variable with the same mean and variance as
![]() $\mathscr{V}(\mathscr{X},\alpha)$
.
$\mathscr{V}(\mathscr{X},\alpha)$
.
Proof. The stabilising part of the proof is inspired by [Reference Penrose and Yukich38], and the idea can also be used to show the stabilisation property for Laguerre tessellations, which are a generalisation of Voronoi tessellations, as in [Reference Flimmel, Pawlas and Yukich23].
Before going into details, we observe that
 \begin{align*} \mathscr{V}\left(\Xi_{\Gamma_{\alpha}},\alpha\right)=&\sum_{\{x,y\}\subset \Xi_{\Gamma_{\alpha}},x\neq y}l\!\left(\partial C\big(x, \Xi_{\Gamma_{\alpha}}\big)\cap \partial C\big(y, \Xi_{\Gamma_{\alpha}}\big)\right)\\ &+l(\partial \Gamma_\alpha),\end{align*}
\begin{align*} \mathscr{V}\left(\Xi_{\Gamma_{\alpha}},\alpha\right)=&\sum_{\{x,y\}\subset \Xi_{\Gamma_{\alpha}},x\neq y}l\!\left(\partial C\big(x, \Xi_{\Gamma_{\alpha}}\big)\cap \partial C\big(y, \Xi_{\Gamma_{\alpha}}\big)\right)\\ &+l(\partial \Gamma_\alpha),\end{align*}
where
![]() $l({\cdot})$
is the volume of a set in dimension
$l({\cdot})$
is the volume of a set in dimension
![]() $d-1$
. We restrict our attention to Voronoi tessellations of random point sets in
$d-1$
. We restrict our attention to Voronoi tessellations of random point sets in
![]() $\mathbb{R}^2$
; with greater notational complexity, the approach also works in
$\mathbb{R}^2$
; with greater notational complexity, the approach also works in
![]() $\mathbb{R}^d$
with
$\mathbb{R}^d$
with
![]() $d\ge3$
, using cones instead of triangles. Because
$d\ge3$
, using cones instead of triangles. Because
![]() $l(\partial \Gamma_\alpha)=4\alpha^{\frac{1}{2}}$
is a constant, by removing this constant, we have
$l(\partial \Gamma_\alpha)=4\alpha^{\frac{1}{2}}$
is a constant, by removing this constant, we have
![]() $\mathscr{V}^{\,\,\prime}\!\left(\Xi_{\Gamma_{\alpha}},\alpha\right)\,:\!=\,\mathscr{V}\left(\Xi_{\Gamma_{\alpha}},\alpha\right)-4\alpha^{\frac{1}{2}}$
and
$\mathscr{V}^{\,\,\prime}\!\left(\Xi_{\Gamma_{\alpha}},\alpha\right)\,:\!=\,\mathscr{V}\left(\Xi_{\Gamma_{\alpha}},\alpha\right)-4\alpha^{\frac{1}{2}}$
and
![]() $d_{TV}\!\left(\mathscr{V}\left(\Xi_{\Gamma_{\alpha}}, \alpha\right),{\bar{Z}}_\alpha\right)=d_{TV}\!\left(\mathscr{V}^{\,\,\prime}\!\left(\Xi_{\Gamma_{\alpha}},\alpha\right),{\bar{Z}}^{\prime}_\alpha\right)$
, where
$d_{TV}\!\left(\mathscr{V}\left(\Xi_{\Gamma_{\alpha}}, \alpha\right),{\bar{Z}}_\alpha\right)=d_{TV}\!\left(\mathscr{V}^{\,\,\prime}\!\left(\Xi_{\Gamma_{\alpha}},\alpha\right),{\bar{Z}}^{\prime}_\alpha\right)$
, where
![]() ${\bar{Z}}^{\prime}_\alpha$
is a normal random variable having the same mean and variance as
${\bar{Z}}^{\prime}_\alpha$
is a normal random variable having the same mean and variance as
![]() $\mathscr{V}^{\,\,\prime}\!\left(\Xi_{\Gamma_{\alpha}},\alpha\right)$
. We can set the score function corresponding to
$\mathscr{V}^{\,\,\prime}\!\left(\Xi_{\Gamma_{\alpha}},\alpha\right)$
. We can set the score function corresponding to
![]() $\mathscr{V}^{\,\,\prime}$
as
$\mathscr{V}^{\,\,\prime}$
as
for all
![]() $x\in \mathscr{X}\subset \Gamma_\alpha$
, i.e.,
$x\in \mathscr{X}\subset \Gamma_\alpha$
, i.e.,
![]() $\eta(x,\mathscr{X},\Gamma_\alpha)$
is half of the total length of edges of
$\eta(x,\mathscr{X},\Gamma_\alpha)$
is half of the total length of edges of
![]() $C(x, \mathscr{X}\,)\cap \Gamma_\alpha$
, excluding the boundary of
$C(x, \mathscr{X}\,)\cap \Gamma_\alpha$
, excluding the boundary of
![]() $\Gamma_\alpha$
. The score function
$\Gamma_\alpha$
. The score function
![]() $\eta$
is clearly translation-invariant. Thus, to apply Theorem 2.2, we need to verify the stabilisation in Definition 2.2, the moment condition (2.4), and the non-singularity in Assumption 2.4.
$\eta$
is clearly translation-invariant. Thus, to apply Theorem 2.2, we need to verify the stabilisation in Definition 2.2, the moment condition (2.4), and the non-singularity in Assumption 2.4.

Figure 7. Voronoi: stabilisation.
We start by showing that the score function is exponentially stabilising. Referring to Figure 7, similarly to Section 3.1, we construct six disjoint equilateral triangles
![]() $T_{xj}(t)$
,
$T_{xj}(t)$
,
![]() $1\le j\le 6$
, such that x is a vertex of these triangles, and the triangles are rotated so that all edges with x as a vertex have angles at least
$1\le j\le 6$
, such that x is a vertex of these triangles, and the triangles are rotated so that all edges with x as a vertex have angles at least
![]() $\pi/12$
relative to the edges of
$\pi/12$
relative to the edges of
![]() $\Gamma_\alpha$
. Let
$\Gamma_\alpha$
. Let
![]() $T_{xj}(\infty)=\cup_{t\ge 0} T_{xj}(t)$
,
$T_{xj}(\infty)=\cup_{t\ge 0} T_{xj}(t)$
,
![]() $1\le j\le 6$
; then
$1\le j\le 6$
; then
![]() $\cup_{1\le j\le 6}T_{xj}(\infty)=\mathbb{R}^2$
. Define
$\cup_{1\le j\le 6}T_{xj}(\infty)=\mathbb{R}^2$
. Define
and
We note that there is a minor issue with the counterpart of
![]() $R_{x0}$
defined in [Reference McGivney and Yukich34] when x is close to the corners of
$R_{x0}$
defined in [Reference McGivney and Yukich34] when x is close to the corners of
![]() $\Gamma_\alpha$
. We now show that
$\Gamma_\alpha$
. We now show that
![]() $\bar{R}(x,\alpha)\,:\!=\,3R_{x0}\big(x,\alpha,\Xi_{\Gamma_\alpha}\big)$
is a radius of stabilisation. In fact, for any point x
′ in
$\bar{R}(x,\alpha)\,:\!=\,3R_{x0}\big(x,\alpha,\Xi_{\Gamma_\alpha}\big)$
is a radius of stabilisation. In fact, for any point x
′ in
![]() $\Gamma_\alpha\backslash \overline{\left(\cup_{1\le j\le 6}T_{xj}(R_{x0})\right)}$
, x
′ is contained in a triangle
$\Gamma_\alpha\backslash \overline{\left(\cup_{1\le j\le 6}T_{xj}(R_{x0})\right)}$
, x
′ is contained in a triangle
![]() $T_{xj_0}(\infty)\backslash\overline{T_{xj_0}(R_{x0})}$
. This implies that
$T_{xj_0}(\infty)\backslash\overline{T_{xj_0}(R_{x0})}$
. This implies that
![]() $T_{xj_0}(R_{x0})\cap \Xi_{\Gamma_\alpha}\ne\emptyset$
, i.e., we can find a point
$T_{xj_0}(R_{x0})\cap \Xi_{\Gamma_\alpha}\ne\emptyset$
, i.e., we can find a point
![]() $y\in T_{xj_0}(R_{x0})\cap \Xi_{\Gamma_\alpha}$
and the point y satisfies
$y\in T_{xj_0}(R_{x0})\cap \Xi_{\Gamma_\alpha}$
and the point y satisfies
![]() $d(x^{\prime},y)\le d(x,x^{\prime})$
; hence
$d(x^{\prime},y)\le d(x,x^{\prime})$
; hence
![]() $x^{\prime}\notin C(x,\Xi_{\Gamma_\alpha})\cap \Gamma_\alpha$
, which ensures that
$x^{\prime}\notin C(x,\Xi_{\Gamma_\alpha})\cap \Gamma_\alpha$
, which ensures that
![]() $C(x,\Xi_{\Gamma_\alpha})\subset \overline{\left(\cup_{1\le j\le 6}T_{xj}(R_0)\right)}$
. Consequently, if a point y in
$C(x,\Xi_{\Gamma_\alpha})\subset \overline{\left(\cup_{1\le j\le 6}T_{xj}(R_0)\right)}$
. Consequently, if a point y in
![]() $\Xi_{\Gamma_\alpha}$
generates an edge of
$\Xi_{\Gamma_\alpha}$
generates an edge of
![]() $C(X)\cap\Gamma_\alpha$
, then
$C(X)\cap\Gamma_\alpha$
, then
![]() $d(x,y)\le 2R_0$
, and
$d(x,y)\le 2R_0$
, and
![]() $\bar{R}(x,\alpha)$
satisfies Definition 2.2. As in Section 3.1, we use
$\bar{R}(x,\alpha)$
satisfies Definition 2.2. As in Section 3.1, we use
![]() $A_t$
in Figure 4 again to define
$A_t$
in Figure 4 again to define
![]() $\tau\,:\!=\,\inf\{t\,:\,|\Xi\cap A_t|\ge 1\}$
; then
$\tau\,:\!=\,\inf\{t\,:\,|\Xi\cap A_t|\ge 1\}$
; then
This completes the proof of the exponential stabilisation of
![]() $\eta$
.
$\eta$
.
The non-singularity in Assumption 2.4 can be examined by using a non-restricted counterpart
![]() $\bar{\eta}$
of
$\bar{\eta}$
of
![]() $\eta$
, taking
$\eta$
, taking
![]() $N_0 =B(0,1)$
, and filling the moat
$N_0 =B(0,1)$
, and filling the moat
![]() $B(0,4)\backslash B(0,3)$
with sufficiently dense points of
$B(0,4)\backslash B(0,3)$
with sufficiently dense points of
![]() $\Xi$
such that, when
$\Xi$
such that, when
![]() $\Xi_{N_0^c}$
is fixed, the random score functions contributing to the sum of (2.6) are purely determined by a point in
$\Xi_{N_0^c}$
is fixed, the random score functions contributing to the sum of (2.6) are purely determined by a point in
![]() $\Xi\cap N_0$
. More precisely, we cover the circle
$\Xi\cap N_0$
. More precisely, we cover the circle
![]() $\partial B(0,3)$
with disjoint squares having side length
$\partial B(0,3)$
with disjoint squares having side length
![]() $\sqrt{2}/4$
, and enumerate the squares as
$\sqrt{2}/4$
, and enumerate the squares as
![]() $S_i,\ 1\le i\le k$
. Note that all the squares are contained in
$S_i,\ 1\le i\le k$
. Note that all the squares are contained in
![]() $B(0,4)\backslash B(0,2)$
. Let
$B(0,4)\backslash B(0,2)$
. Let
![]() $E=\cap_{1\le i\le k}\{|\Xi\cap(S_i)|\ge 1\}$
,
$E=\cap_{1\le i\le k}\{|\Xi\cap(S_i)|\ge 1\}$
,
![]() $E_1=\{|\Xi\cap N_0|=1\}$
; then E is
$E_1=\{|\Xi\cap N_0|=1\}$
; then E is
![]() $\sigma\Big(\Xi_{N_0^c}\Big)$
-measurable,
$\sigma\Big(\Xi_{N_0^c}\Big)$
-measurable,
![]() $\mathbb{P}(E)>0$
, and
$\mathbb{P}(E)>0$
, and
![]() $\mathbb{P}(E_1|E)>0$
. Since the points in
$\mathbb{P}(E_1|E)>0$
. Since the points in
![]() $\Xi\cap \left(\cup_{i=1}^kS_i\right)$
have neighbours within distance 1, for any
$\Xi\cap \left(\cup_{i=1}^kS_i\right)$
have neighbours within distance 1, for any
![]() $x\in N_0$
,
$x\in N_0$
,
![]() $T_{xj}(6)$
contains at least one point from
$T_{xj}(6)$
contains at least one point from
![]() $\Xi\cap \left(B(0,4)\backslash B(0,2)\right)$
. As argued in the stabilisation, points in
$\Xi\cap \left(B(0,4)\backslash B(0,2)\right)$
. As argued in the stabilisation, points in
![]() $\Xi\cap \left(B(0,12)^c\right)$
do not affect the cell centred at
$\Xi\cap \left(B(0,12)^c\right)$
do not affect the cell centred at
![]() $x\in N_0$
, and by symmetry,
$x\in N_0$
, and by symmetry,
![]() $x\in N_0$
does not affect the Voronoi cells centred at points in
$x\in N_0$
does not affect the Voronoi cells centred at points in
![]() $\Xi\cap \left(B(0,12)^c\right)$
. This ensures that, conditional on E, all random score functions contributing to the sum of (2.6) are those completely determined by
$\Xi\cap \left(B(0,12)^c\right)$
. This ensures that, conditional on E, all random score functions contributing to the sum of (2.6) are those completely determined by
![]() $\Xi_{N_0}$
, giving
$\Xi_{N_0}$
, giving

where X is
![]() $\sigma\Big(\Xi_{N_0^c}\Big)$
-measurable. As
$\sigma\Big(\Xi_{N_0^c}\Big)$
-measurable. As
![]() $\textbf{1}_{E_1}\bar{\eta}\!\left(x,\Xi\right)$
is an almost surely (a.s.) (in terms of the volume measure in
$\textbf{1}_{E_1}\bar{\eta}\!\left(x,\Xi\right)$
is an almost surely (a.s.) (in terms of the volume measure in
![]() $\mathbb{R}^2$
) continuous function of
$\mathbb{R}^2$
) continuous function of
![]() $x\in \Xi\cap N_0$
, the proof of the non-singularity in Assumption 2.4 is completed.
$x\in \Xi\cap N_0$
, the proof of the non-singularity in Assumption 2.4 is completed.
It remains to show the moment condition (2.4). In fact, as shown in the stabilisation property, we can see that
![]() $\bar{R}(x,\alpha)$
will not increase when points are added, so
$\bar{R}(x,\alpha)$
will not increase when points are added, so
![]() $C\big(x_3,\Xi_{\Gamma_\alpha}+a_1\delta_{x_1}+a_2\delta_{x_2}+\delta_{x_3}\big)\cap \Gamma_\alpha\subset B(x, \bar{R}(x,\alpha))$
; then the number of edges of
$C\big(x_3,\Xi_{\Gamma_\alpha}+a_1\delta_{x_1}+a_2\delta_{x_2}+\delta_{x_3}\big)\cap \Gamma_\alpha\subset B(x, \bar{R}(x,\alpha))$
; then the number of edges of
![]() $C\big(x_3,\Xi_{\Gamma_\alpha}+a_1\delta_{x_1}+a_2\delta_{x_2}+\delta_{x_3}\big)\cap \Gamma_\alpha$
excluding those in the edge of
$C\big(x_3,\Xi_{\Gamma_\alpha}+a_1\delta_{x_1}+a_2\delta_{x_2}+\delta_{x_3}\big)\cap \Gamma_\alpha$
excluding those in the edge of
![]() $ \Gamma_\alpha$
is less than or equal to
$ \Gamma_\alpha$
is less than or equal to
![]() $(\Xi_{\Gamma_\alpha}+a_1\delta_{x_1}+a_2\delta_{x_2})\left(B\!\left(x,\bar{R}(x{,\alpha})\right)\right)\le\Xi_{\Gamma_\alpha}\left(B\!\left(x,\bar{R}(x{,\alpha})\right)\right)+2$
, and each of them has length less than
$(\Xi_{\Gamma_\alpha}+a_1\delta_{x_1}+a_2\delta_{x_2})\left(B\!\left(x,\bar{R}(x{,\alpha})\right)\right)\le\Xi_{\Gamma_\alpha}\left(B\!\left(x,\bar{R}(x{,\alpha})\right)\right)+2$
, and each of them has length less than
![]() $2\bar{R}(x,\alpha)$
. We observe that
$2\bar{R}(x,\alpha)$
. We observe that
![]() $\Xi$
restricted to outside of
$\Xi$
restricted to outside of
![]() $\cup_{j=1}^6T_{xj}(R_{xj})$
is independent of
$\cup_{j=1}^6T_{xj}(R_{xj})$
is independent of
![]() $\bar{R}(x,\alpha)$
; hence
$\bar{R}(x,\alpha)$
; hence
where
stands for ‘stochastically less than or equal to’, and
![]() $\Xi^{\prime}$
is an independent copy of
$\Xi^{\prime}$
is an independent copy of
![]() $\Xi$
. Therefore, using (3.4), we obtain
$\Xi$
. Therefore, using (3.4), we obtain
 \begin{align*} &\mathbb{E}\!\left(\eta\!\left(x_3,\Xi_{\Gamma_\alpha}+a_1\delta_{x_1}+a_2\delta_{x_2}+\delta_{x_3}\right)^3\right)\\ \le&\mathbb{E}\!\left(\left(\Xi^{\prime}\left(B\!\left({x_3},\bar{R}(x{,\alpha})\right)\right)+8\right)^3\left(2\bar{R}({x_3}{,\alpha})\right)^3\right)\\ \le &\int_0^\infty \sum_{i=0}^\infty (i+8)^3(2r)^3\frac{e^{-\lambda \pi r^2} \big(\lambda \pi r^2\big)^i}{i!}6e^{-0.116\lambda (t/3)^2}*\left(0.116\lambda/9\right)2rdr\\ \le& C<\infty,\end{align*}
\begin{align*} &\mathbb{E}\!\left(\eta\!\left(x_3,\Xi_{\Gamma_\alpha}+a_1\delta_{x_1}+a_2\delta_{x_2}+\delta_{x_3}\right)^3\right)\\ \le&\mathbb{E}\!\left(\left(\Xi^{\prime}\left(B\!\left({x_3},\bar{R}(x{,\alpha})\right)\right)+8\right)^3\left(2\bar{R}({x_3}{,\alpha})\right)^3\right)\\ \le &\int_0^\infty \sum_{i=0}^\infty (i+8)^3(2r)^3\frac{e^{-\lambda \pi r^2} \big(\lambda \pi r^2\big)^i}{i!}6e^{-0.116\lambda (t/3)^2}*\left(0.116\lambda/9\right)2rdr\\ \le& C<\infty,\end{align*}
which ensures (2.4). The proof of Theorem 3.2 is completed by using Theorem 2.2.
3.3. Timber volume estimation
Timber volume estimation is an essential research topic in forest science and forest management [Reference Cailliez8, Reference Li, Barclay, Hans and Sidders32]. This example demonstrates that, with the marks, our theorem can be used to provide an error estimate for the normal approximation of the timber volume distribution. To this end, it is reasonable to assume that in a given range
![]() $\Gamma_\alpha$
of a natural forest, the locations of trees form a Poisson point process
$\Gamma_\alpha$
of a natural forest, the locations of trees form a Poisson point process
![]() $\bar{\Xi}$
. For
$\bar{\Xi}$
. For
![]() $x\in \bar{\Xi}$
, we can use a random mark
$x\in \bar{\Xi}$
, we can use a random mark
![]() $M_x\in{T}\,:\!=\,\{1,\dots,n\}$
to denote the species of the tree at position x; then
$M_x\in{T}\,:\!=\,\{1,\dots,n\}$
to denote the species of the tree at position x; then
![]() $\Xi\,:\!=\,\sum_{x\in \bar{\Xi}}\delta_{(x,M_x)}$
is a marked Poisson point process with independent marks. The timber volume of a tree at x is a combined result of the location, the species of the tree, the configuration of species of trees in a finite range around x, and some other random factors that cannot be explained by the configuration of trees in the range. We write
$\Xi\,:\!=\,\sum_{x\in \bar{\Xi}}\delta_{(x,M_x)}$
is a marked Poisson point process with independent marks. The timber volume of a tree at x is a combined result of the location, the species of the tree, the configuration of species of trees in a finite range around x, and some other random factors that cannot be explained by the configuration of trees in the range. We write
![]() $\eta(\left(x,m\right)\!, \Xi_{\Gamma_\alpha},\Gamma_\alpha)$
as the timber volume determined by the location x, the species m, and the configuration of trees, and
$\eta(\left(x,m\right)\!, \Xi_{\Gamma_\alpha},\Gamma_\alpha)$
as the timber volume determined by the location x, the species m, and the configuration of trees, and
![]() ${\epsilon}_{x}$
as the adjusted timber volume at location x due to unexplained random factors.
${\epsilon}_{x}$
as the adjusted timber volume at location x due to unexplained random factors.
Theorem 3.3.
Assume that
![]() $\eta$
is a non-negative bounded score function such that
$\eta$
is a non-negative bounded score function such that
for some positive constant r,
for all
![]() $\alpha_1$
and
$\alpha_1$
and
![]() $\alpha_2$
with
$\alpha_2$
with
![]() $B(x,r)\subset \Gamma_{\alpha_1\wedge\alpha_2}$
,
$B(x,r)\subset \Gamma_{\alpha_1\wedge\alpha_2}$
,
![]() $\eta$
is translation-invariant as in Definition 2.4, the
$\eta$
is translation-invariant as in Definition 2.4, the
![]() ${\epsilon}_{x}$
are i.i.d. random variables with a finite third moment, the positive part
${\epsilon}_{x}$
are i.i.d. random variables with a finite third moment, the positive part
![]() ${\epsilon}_x^+=\max\!({\epsilon}_x,0)$
is non-singular, and the
${\epsilon}_x^+=\max\!({\epsilon}_x,0)$
is non-singular, and the
![]() ${\epsilon}_{x}$
are independent of the configuration
${\epsilon}_{x}$
are independent of the configuration
![]() $\Xi$
. Then the timber volume of the range
$\Xi$
. Then the timber volume of the range
![]() $\Gamma_\alpha$
can be represented as
$\Gamma_\alpha$
can be represented as
and it satisfies
where
![]() ${\bar{Z}}_\alpha$
is a normal random variable with the same mean and variance as
${\bar{Z}}_\alpha$
is a normal random variable with the same mean and variance as
![]() ${\bar{W}}_\alpha$
.
${\bar{W}}_\alpha$
.
Proof. Before going into details, we first construct a new marked Poisson point process
![]() $\Xi^{\prime}\,:\!=\,\sum_{x\in \bar{\Xi}}\delta_{(x, (M_x, {\epsilon}_x))}$
with i.i.d. marks
$\Xi^{\prime}\,:\!=\,\sum_{x\in \bar{\Xi}}\delta_{(x, (M_x, {\epsilon}_x))}$
with i.i.d. marks
![]() $(M_x,{\epsilon}_x)\in T\times \mathbb{R}$
independent of the ground process
$(M_x,{\epsilon}_x)\in T\times \mathbb{R}$
independent of the ground process
![]() $\bar{\Xi}^{\prime}=\bar{\Xi}$
, and incorporate
$\bar{\Xi}^{\prime}=\bar{\Xi}$
, and incorporate
![]() ${\epsilon}_x$
into a new score function on
${\epsilon}_x$
into a new score function on
![]() $\Xi^{\prime}$
as
$\Xi^{\prime}$
as
 \begin{align*} \eta^{\prime}((x,{(m,{\epsilon})}),\Xi^{\prime},\Gamma_\alpha)\,:\!=\,&\eta^{\prime}((x,(m,{\epsilon})),\Xi^{\prime}_{\Gamma_\alpha},\Gamma_\alpha)\\ \,:\!=\,&\left[\left(\eta(\left(x,m\right)\!, \Xi_{\Gamma_\alpha},\Gamma_\alpha)+{\epsilon}\right)\vee 0\right]\textbf{1}_{(x,(m,{\epsilon}))\in \Xi^{\prime}_{\Gamma_\alpha}}.\end{align*}
\begin{align*} \eta^{\prime}((x,{(m,{\epsilon})}),\Xi^{\prime},\Gamma_\alpha)\,:\!=\,&\eta^{\prime}((x,(m,{\epsilon})),\Xi^{\prime}_{\Gamma_\alpha},\Gamma_\alpha)\\ \,:\!=\,&\left[\left(\eta(\left(x,m\right)\!, \Xi_{\Gamma_\alpha},\Gamma_\alpha)+{\epsilon}\right)\vee 0\right]\textbf{1}_{(x,(m,{\epsilon}))\in \Xi^{\prime}_{\Gamma_\alpha}}.\end{align*}
We can see that
The score function
![]() $\eta^{\prime}$
is clearly translation-invariant. Thus, to apply Theorem 2.2, it is sufficient to verify that
$\eta^{\prime}$
is clearly translation-invariant. Thus, to apply Theorem 2.2, it is sufficient to verify that
![]() $\eta^{\prime}$
is range-bounded as in Definition 2.2 and satisfies the moment condition (2.4) and the non-singularity in Assumption 2.4.
$\eta^{\prime}$
is range-bounded as in Definition 2.2 and satisfies the moment condition (2.4) and the non-singularity in Assumption 2.4.
The range-bounded property of the score function
![]() $\eta^{\prime}$
is inherited from the range-bounded property of
$\eta^{\prime}$
is inherited from the range-bounded property of
![]() $\eta$
with the same radius of stabilisation
$\eta$
with the same radius of stabilisation
![]() $\bar{R}(x,\alpha)\,:\!=\,r$
. The moment condition (2.4) is a direct consequence of the boundedness of
$\bar{R}(x,\alpha)\,:\!=\,r$
. The moment condition (2.4) is a direct consequence of the boundedness of
![]() $\eta$
, the finite third moment of
$\eta$
, the finite third moment of
![]() ${\epsilon}_x$
, and the Minkowski inequality. Hence it remains to show the non-singularity. To this end, we observe that the corresponding unrestricted counterpart
${\epsilon}_x$
, and the Minkowski inequality. Hence it remains to show the non-singularity. To this end, we observe that the corresponding unrestricted counterpart
![]() $\bar{\eta}$
of
$\bar{\eta}$
of
![]() $\eta^{\prime}$
is defined by
$\eta^{\prime}$
is defined by
 \begin{align*} \bar{\eta}\big((x,(m_x,{\epsilon}_x)),\mathscr{X}^{\,\prime}\big)&= \lim_{\alpha\rightarrow \infty}\eta^{\prime}\big((x,(m_x,{\epsilon}_x)),\mathscr{X}^{\,\prime},\Gamma_{\alpha}\big)\\ &=\eta^{\prime}\big((x,(m_x,{\epsilon}_x)),\mathscr{X}^{\,\prime},\Gamma_{\alpha_x}\big)= \left(\eta\big((x,m_x),\mathscr{X},\Gamma_{\alpha_x}\big)+{\epsilon}_x\right)\vee 0,\end{align*}
\begin{align*} \bar{\eta}\big((x,(m_x,{\epsilon}_x)),\mathscr{X}^{\,\prime}\big)&= \lim_{\alpha\rightarrow \infty}\eta^{\prime}\big((x,(m_x,{\epsilon}_x)),\mathscr{X}^{\,\prime},\Gamma_{\alpha}\big)\\ &=\eta^{\prime}\big((x,(m_x,{\epsilon}_x)),\mathscr{X}^{\,\prime},\Gamma_{\alpha_x}\big)= \left(\eta\big((x,m_x),\mathscr{X},\Gamma_{\alpha_x}\big)+{\epsilon}_x\right)\vee 0,\end{align*}
where
![]() $\alpha_x=4(\|x\|+r)^2$
, and
$\alpha_x=4(\|x\|+r)^2$
, and
![]() $\mathscr{X}$
is the projection of
$\mathscr{X}$
is the projection of
![]() $\mathscr{X}^{\,\prime}$
on
$\mathscr{X}^{\,\prime}$
on
![]() $\mathbb{R}^2\times T$
. Let
$\mathbb{R}^2\times T$
. Let
![]() $N_0=B(0,1)$
, and let
$N_0=B(0,1)$
, and let
then E is
![]() $\sigma\!\left(\Xi^{\prime}_{N_0^c}\right)$
-measurable,
$\sigma\!\left(\Xi^{\prime}_{N_0^c}\right)$
-measurable,
![]() $\mathbb{P}(E)>0$
, and
$\mathbb{P}(E)>0$
, and
![]() $\mathbb{P}(E_1|E)>0$
. Writing
$\mathbb{P}(E_1|E)>0$
. Writing
![]() ${\epsilon}_x^-=-\min\!({\epsilon}_x,0)$
,
${\epsilon}_x^-=-\min\!({\epsilon}_x,0)$
,
![]() $\bar{\Xi}^{\prime}_{N_0}=\{x_0\}$
in
$\bar{\Xi}^{\prime}_{N_0}=\{x_0\}$
in
![]() $E_1$
, given E we have
$E_1$
, given E we have
 \begin{align*} &\quad \textbf{1}_{E_1}\sum_{x\in\bar{\Xi^{\prime}}}\bar{\eta}\!\left((x,(m_x,{\epsilon}_x)),\Xi^{\prime}\right)\textbf{1}_{d(x, N_0)<r}\\ &=\textbf{1}_{E_1} \!\left(\eta\big(\big(x_0,m_{x_0}\big),\delta_{\big({x_0},m_{x_0}\big)},\Gamma_{4(r+1)^2}\big)+{{\epsilon}_{x_0}}\right)\vee0 \\ &= \textbf{1}_{E_1}\!\left[\textbf{1}_{{{\epsilon}_{x_0}}>0}\left(\eta\big(\big({x_0},m_{x_0}\big),\delta_{\big({x_0},m_{x_0}\big)},\Gamma_{4(r+1)^2}\big)+{\epsilon}_{x_0}^+\right)\right.\\ & \quad +\left.\textbf{1}_{{\epsilon}_{x_0}\le 0}\left(\eta\big(\big({x_0},m_{x_0}\big),\delta_{\big({x_0},m_{x_0}\big)},\Gamma_{4(r+1)^2}\big)-{\epsilon}_{x_0}^-\right)\right]\vee 0.\end{align*}
\begin{align*} &\quad \textbf{1}_{E_1}\sum_{x\in\bar{\Xi^{\prime}}}\bar{\eta}\!\left((x,(m_x,{\epsilon}_x)),\Xi^{\prime}\right)\textbf{1}_{d(x, N_0)<r}\\ &=\textbf{1}_{E_1} \!\left(\eta\big(\big(x_0,m_{x_0}\big),\delta_{\big({x_0},m_{x_0}\big)},\Gamma_{4(r+1)^2}\big)+{{\epsilon}_{x_0}}\right)\vee0 \\ &= \textbf{1}_{E_1}\!\left[\textbf{1}_{{{\epsilon}_{x_0}}>0}\left(\eta\big(\big({x_0},m_{x_0}\big),\delta_{\big({x_0},m_{x_0}\big)},\Gamma_{4(r+1)^2}\big)+{\epsilon}_{x_0}^+\right)\right.\\ & \quad +\left.\textbf{1}_{{\epsilon}_{x_0}\le 0}\left(\eta\big(\big({x_0},m_{x_0}\big),\delta_{\big({x_0},m_{x_0}\big)},\Gamma_{4(r+1)^2}\big)-{\epsilon}_{x_0}^-\right)\right]\vee 0.\end{align*}
On
![]() $\{{\epsilon}_{x_0}>0\}$
,
$\{{\epsilon}_{x_0}>0\}$
,
![]() ${\epsilon}_{x_0}^+$
is independent of
${\epsilon}_{x_0}^+$
is independent of
![]() $\eta\Big(\big({x_0},m_{x_0}\big),\delta_{\big({x_0},m_{x_0}\big)},\Gamma_{4(r+1)^2}\Big)$
and has a positive non-singular component; hence
$\eta\Big(\big({x_0},m_{x_0}\big),\delta_{\big({x_0},m_{x_0}\big)},\Gamma_{4(r+1)^2}\Big)$
and has a positive non-singular component; hence
![]() $\eta\Big(\big({x_0},m_{x_0}\big),\delta_{\big({x_0},m_{x_0}\big)},\Gamma_{4(r+1)^2}\Big)+{\epsilon}_{x_0}^+$
is also non-singular. Together with the fact that
$\eta\Big(\big({x_0},m_{x_0}\big),\delta_{\big({x_0},m_{x_0}\big)},\Gamma_{4(r+1)^2}\Big)+{\epsilon}_{x_0}^+$
is also non-singular. Together with the fact that
![]() $\{{\epsilon}_{x_0}>0\}$
and
$\{{\epsilon}_{x_0}>0\}$
and
![]() $\{{\epsilon}_{x_0}\le 0\}$
are disjoint, this implies the non-singularity.
$\{{\epsilon}_{x_0}\le 0\}$
are disjoint, this implies the non-singularity.
Remark 3.2. If the timber volume of a tree is determined by its nearest neighbouring trees, then we can set the score function
![]() $\eta$
as a function of weighted Voronoi cells. Using the idea of the proof of Theorem 3.2, we can establish the bound of the error of the normal approximation to the distribution of the timber volume
$\eta$
as a function of weighted Voronoi cells. Using the idea of the proof of Theorem 3.2, we can establish the bound of the error of the normal approximation to the distribution of the timber volume
![]() ${\bar{W}}_\alpha$
as
${\bar{W}}_\alpha$
as
![]() $d_{TV}\!\left({\bar{W}}_\alpha,{\bar{Z}}_\alpha\right)\le \mathop{{}\textrm{O}}\mathopen{}\big(\alpha^{-\frac{1}{2}}\ln\!(\alpha)^{\frac{5d}{2}}\big)$
. Furthermore, by setting
$d_{TV}\!\left({\bar{W}}_\alpha,{\bar{Z}}_\alpha\right)\le \mathop{{}\textrm{O}}\mathopen{}\big(\alpha^{-\frac{1}{2}}\ln\!(\alpha)^{\frac{5d}{2}}\big)$
. Furthermore, by setting
![]() $\eta((x,m_x),\Xi,\Gamma_{\alpha})$
as a function of the
$\eta((x,m_x),\Xi,\Gamma_{\alpha})$
as a function of the
![]() $k_{m_x}$
nearest neighbourhoods of x instead of the configuration of species of trees in a bounded neighbourhood, we gain an example with stabilising radius R depending not only on x but also on
$k_{m_x}$
nearest neighbourhoods of x instead of the configuration of species of trees in a bounded neighbourhood, we gain an example with stabilising radius R depending not only on x but also on
![]() $m_x$
.
$m_x$
.
3.4. Maximal layers
Maximal layers of points have been of considerable interest since [Reference Rényi42, Reference Kung, Luccio and Preparata29], and have a wide range of applications; see [Reference Chen, Hwang and Tsai11] for a brief review of their applications. One of the applications is the smallest colour-spanning interval [Reference Khanteimouri28], which is a linear function of the distances between maximal points and the edge. In this subsection, we demonstrate that Theorem 2.2 with marks can easily be applied to estimate the error of the normal approximation to the distribution of the sum of distances between different maximal layers if the points are from a Poisson point process.
For
![]() $x\in \mathbb{R}^d$
, we define
$x\in \mathbb{R}^d$
, we define
![]() $A_x=([0,\infty)^d+x)\cap\Gamma_\alpha$
. Given a locally finite point set
$A_x=([0,\infty)^d+x)\cap\Gamma_\alpha$
. Given a locally finite point set
![]() $\mathscr{X}\subset \mathbb{R}^d$
, a point x is called maximal in
$\mathscr{X}\subset \mathbb{R}^d$
, a point x is called maximal in
![]() $\mathscr{X}$
if
$\mathscr{X}$
if
![]() $x\in\mathscr{X}$
and there is no other point
$x\in\mathscr{X}$
and there is no other point
![]() $(y_1,\dots,y_d)\in \mathscr{X}$
satisfying
$(y_1,\dots,y_d)\in \mathscr{X}$
satisfying
![]() $y_i\ge x_i$
for all
$y_i\ge x_i$
for all
![]() $1\le i\le d$
(see Figure 8(a)). Mathematically, x is maximal in
$1\le i\le d$
(see Figure 8(a)). Mathematically, x is maximal in
![]() $\mathscr{X}$
if
$\mathscr{X}$
if
![]() $\mathscr{X}\cap A_x=\{x\}$
. This enables us to write different maximal layers as follows: the kth maximal layer of points can be recursively defined as
$\mathscr{X}\cap A_x=\{x\}$
. This enables us to write different maximal layers as follows: the kth maximal layer of points can be recursively defined as
with the convention
![]() $\cup_{i=1}^0\mathscr{X}_i=\emptyset$
.
$\cup_{i=1}^0\mathscr{X}_i=\emptyset$
.

Figure 8. Maximal layers.
For simplicity, we consider the restriction of the Poisson point process to a region in
![]() $\mathbb{R}^d$
between two parallel
$\mathbb{R}^d$
between two parallel
![]() $(d-1)$
-dimensional planes for
$(d-1)$
-dimensional planes for
![]() $d\ge2$
. More precisely, the region of interest is
$d\ge2$
. More precisely, the region of interest is
 \begin{equation*}\Gamma_{\alpha,r}=\left\{(x_1,x_2,\dots,x_d);\,x_i\in\big[0,\alpha^{\frac{1}{d-1}}\big], i\le d-1,x_d+\sum_{i=1}^{d-1}x_i \cot\!(\theta_i)\in[0,r]\right\}\end{equation*}
\begin{equation*}\Gamma_{\alpha,r}=\left\{(x_1,x_2,\dots,x_d);\,x_i\in\big[0,\alpha^{\frac{1}{d-1}}\big], i\le d-1,x_d+\sum_{i=1}^{d-1}x_i \cot\!(\theta_i)\in[0,r]\right\}\end{equation*}
for fixed
![]() $\theta_i\in\big(0,\frac{\pi}{2}\big)$
,
$\theta_i\in\big(0,\frac{\pi}{2}\big)$
,
![]() $1\le i\le d-1$
, and
$1\le i\le d-1$
, and
![]() $\Xi_{\Gamma_{\alpha,r}}$
is a homogeneous Poisson point process with rate
$\Xi_{\Gamma_{\alpha,r}}$
is a homogeneous Poisson point process with rate
![]() $\lambda$
on
$\lambda$
on
![]() $\Gamma_{\alpha,r}$
. Define
$\Gamma_{\alpha,r}$
. Define
![]() $\Xi_{k,r,\alpha}$
as the kth maximal layer of
$\Xi_{k,r,\alpha}$
as the kth maximal layer of
![]() $\Xi_{\Gamma_{\alpha,r}}$
; then the total distance between the points in
$\Xi_{\Gamma_{\alpha,r}}$
; then the total distance between the points in
![]() $\Xi_{k,r,\alpha}$
and the upper plane
$\Xi_{k,r,\alpha}$
and the upper plane
 \begin{equation*}P\,:\!=\,\left\{(x_1,x_2,\dots,x_d);\,x_i\in \big[0,\alpha^{\frac{1}{d-1}}\big],\ i\le d-1,x_d=-\sum_{i=1}^{d-1}x_i \cot\!(\theta_i)+r\right\}\end{equation*}
\begin{equation*}P\,:\!=\,\left\{(x_1,x_2,\dots,x_d);\,x_i\in \big[0,\alpha^{\frac{1}{d-1}}\big],\ i\le d-1,x_d=-\sum_{i=1}^{d-1}x_i \cot\!(\theta_i)+r\right\}\end{equation*}
can be represented as
![]() ${\bar{W}}_{k,r,\alpha}\,:\!=\,\sum_{x\in \Xi_{k,r,\alpha}}d(x,P)$
.
${\bar{W}}_{k,r,\alpha}\,:\!=\,\sum_{x\in \Xi_{k,r,\alpha}}d(x,P)$
.
Theorem 3.4.
With the above setup, when
![]() $r\in \mathbb{R}_+$
and
$r\in \mathbb{R}_+$
and
![]() $k\in \mathbb{N}$
is fixed,
$k\in \mathbb{N}$
is fixed,
where
![]() ${\bar{Z}}_{k,r,\alpha}\sim N\!\left(\mathbb{E} \big(\bar{W}_{k,r,\alpha}\big),{\textrm{Var}}\!\left({\bar{W}}_{k,r,\alpha}\right)\right)$
.
${\bar{Z}}_{k,r,\alpha}\sim N\!\left(\mathbb{E} \big(\bar{W}_{k,r,\alpha}\big),{\textrm{Var}}\!\left({\bar{W}}_{k,r,\alpha}\right)\right)$
.
Remark 3.3. It remains a challenge to consider maximal layers induced by a homogeneous Poisson point process on
where
![]() $F\,:\,[0,\alpha^{1/(d-1)} ]^{d-1}\to [0,\infty)$
has continuous negative partial derivatives in all coordinates, the partial derivatives are bounded away from 0 and
$F\,:\,[0,\alpha^{1/(d-1)} ]^{d-1}\to [0,\infty)$
has continuous negative partial derivatives in all coordinates, the partial derivatives are bounded away from 0 and
![]() $-\infty$
, and
$-\infty$
, and
![]() $|F|\le {\mathop{{}\textrm{O}}\mathopen{}(\alpha^{1/(d-1)})}$
. We conjecture that the normal approximation in total variation for the total distance between the points in a maximal layer and the upper edge surface is still valid. The convergence rate of the total number of points in the kth maximal layer under the Kolmogorov distance can be found in [Reference Lachièze-Rey, Schulte and Yukich30, Theorem 3.3], but because the number of points is a discrete random variable, the convergence rate under the total variation distance is always 1.
$|F|\le {\mathop{{}\textrm{O}}\mathopen{}(\alpha^{1/(d-1)})}$
. We conjecture that the normal approximation in total variation for the total distance between the points in a maximal layer and the upper edge surface is still valid. The convergence rate of the total number of points in the kth maximal layer under the Kolmogorov distance can be found in [Reference Lachièze-Rey, Schulte and Yukich30, Theorem 3.3], but because the number of points is a discrete random variable, the convergence rate under the total variation distance is always 1.
Proof of Theorem
3.4. As the score function
![]() $d({\cdot},P)$
is not translation-invariant in the sense of Definition 2.4, we first turn the problem into that of a marked Poisson point process with independent marks. The idea is to project the points of
$d({\cdot},P)$
is not translation-invariant in the sense of Definition 2.4, we first turn the problem into that of a marked Poisson point process with independent marks. The idea is to project the points of
![]() $\Xi_{\Gamma_{\alpha,r}}$
on their first
$\Xi_{\Gamma_{\alpha,r}}$
on their first
![]() $d-1$
coordinates to obtain the ground Poisson point process, and send the last coordinate to marks with
$d-1$
coordinates to obtain the ground Poisson point process, and send the last coordinate to marks with
![]() $T=[0,r]$
. To this end, define a mapping
$T=[0,r]$
. To this end, define a mapping
![]() $h^{\prime}\,:\,\Gamma_{\infty,r}\,:\!=\,\cup_{\alpha>0}\Gamma_{\alpha,r}\rightarrow[0,\infty)^{d-1}\times [0,r]$
such that
$h^{\prime}\,:\,\Gamma_{\infty,r}\,:\!=\,\cup_{\alpha>0}\Gamma_{\alpha,r}\rightarrow[0,\infty)^{d-1}\times [0,r]$
such that
 \begin{equation*}h^{\prime}(x_1,\dots,x_d)=(x_1,\dots,x_d)+\left(0,\dots,0,\sum_{i=1}^{d-1}x_i\cot\!(\theta_i)\right)\end{equation*}
\begin{equation*}h^{\prime}(x_1,\dots,x_d)=(x_1,\dots,x_d)+\left(0,\dots,0,\sum_{i=1}^{d-1}x_i\cot\!(\theta_i)\right)\end{equation*}
and
![]() $h(\mathscr{X}\,)\,:\!=\,\{h^{\prime}(x)\,:\,x\in \mathscr{X}\}$
. Then h
′ is a one-to-one mapping, and
$h(\mathscr{X}\,)\,:\!=\,\{h^{\prime}(x)\,:\,x\in \mathscr{X}\}$
. Then h
′ is a one-to-one mapping, and
![]() $\Xi^{\prime}\,:\!=\,h\!\left(\Xi_{\Gamma_{\infty,r}}\right)$
can be regarded as a marked Poisson point process on
$\Xi^{\prime}\,:\!=\,h\!\left(\Xi_{\Gamma_{\infty,r}}\right)$
can be regarded as a marked Poisson point process on
![]() $[0,\infty)^{d-1}\times [0,r]$
with rate
$[0,\infty)^{d-1}\times [0,r]$
with rate
![]() $r\lambda$
and independent marks following the uniform distribution on [0, r]. Write the mark of
$r\lambda$
and independent marks following the uniform distribution on [0, r]. Write the mark of
![]() $x\in \Xi^{\prime}$
as
$x\in \Xi^{\prime}$
as
![]() $m_x$
; then
$m_x$
; then
where
![]() $C(\theta_1,\dots,\theta_{d-1})$
is a constant determined by
$C(\theta_1,\dots,\theta_{d-1})$
is a constant determined by
![]() $\theta_1,\dots,\theta_{d-1}$
. Let
$\theta_1,\dots,\theta_{d-1}$
. Let
![]() $\Gamma_\alpha^{\prime}\,:\!=\,\big[0,\alpha^{\frac{1}{d-1}}\big]^{d-1}$
; then
$\Gamma_\alpha^{\prime}\,:\!=\,\big[0,\alpha^{\frac{1}{d-1}}\big]^{d-1}$
; then
![]() $h\big(\Xi_{\Gamma_{\alpha,r}}\big)=\Xi^{\prime}_{\Gamma^{\prime}_\alpha}$
. For a point
$h\big(\Xi_{\Gamma_{\alpha,r}}\big)=\Xi^{\prime}_{\Gamma^{\prime}_\alpha}$
. For a point
![]() $(x,m)\in [0,\infty)^{d-1}\times[0,r]$
, we write
$(x,m)\in [0,\infty)^{d-1}\times[0,r]$
, we write
(see Figure 8(b)) and
Combining (3.5) and (3.6), we can represent
![]() ${\bar{W}}_{k,r,\alpha}$
as the sum of values of the score function
${\bar{W}}_{k,r,\alpha}$
as the sum of values of the score function
over the range
![]() $\Gamma^{\prime}_\alpha$
. To apply Theorem 2.2, we need to check that
$\Gamma^{\prime}_\alpha$
. To apply Theorem 2.2, we need to check that
![]() $\eta$
is range-bounded as in Definition 2.2, and that it satisfies the moment condition (2.4) and the non-singularity in Assumption 2.4.
$\eta$
is range-bounded as in Definition 2.2, and that it satisfies the moment condition (2.4) and the non-singularity in Assumption 2.4.
For simplicity, we only show the claim in the two-dimensional case; the argument for
![]() $d>2$
is the same except for notational complexity. When
$d>2$
is the same except for notational complexity. When
![]() $d=2$
,
$d=2$
,
![]() $\Gamma_{\alpha,r}$
is a parallelogram with angle
$\Gamma_{\alpha,r}$
is a parallelogram with angle
![]() $\theta_1$
as in Figure 8(a), and P and
$\theta_1$
as in Figure 8(a), and P and
![]() $C(\theta_1,\dots,\theta_{d-1})$
reduce to an edge in
$C(\theta_1,\dots,\theta_{d-1})$
reduce to an edge in
![]() $\mathbb{R}^2$
and
$\mathbb{R}^2$
and
![]() $\sin\!(\theta_1)$
, respectively. Since
$\sin\!(\theta_1)$
, respectively. Since
![]() $\sin\!(\theta_1)(r-m_x)$
is given by the mark of x, to show
$\sin\!(\theta_1)(r-m_x)$
is given by the mark of x, to show
![]() $\eta$
is range-bounded, it is sufficient to show that
$\eta$
is range-bounded, it is sufficient to show that
![]() $\textbf{1}_{\big\{(x,m_x)\in\Xi^{\prime}_{k,r,\alpha}\big\}}$
is completely determined by
$\textbf{1}_{\big\{(x,m_x)\in\Xi^{\prime}_{k,r,\alpha}\big\}}$
is completely determined by
![]() $\Xi^{\prime}\cap A^{\prime}_{x,m_x,r,\alpha}$
. In fact, we can accomplish this by observing that
$\Xi^{\prime}\cap A^{\prime}_{x,m_x,r,\alpha}$
. In fact, we can accomplish this by observing that
![]() $(x,m_x)\in \Xi^{\prime}_{k,r,\alpha}$
if and only if there is a sequence
$(x,m_x)\in \Xi^{\prime}_{k,r,\alpha}$
if and only if there is a sequence
![]() $\{(x_j,m_{x_j}),\ 1\le j\le k\}\subset \Xi^{\prime}\cap A^{\prime}_{x,m_x,r,\alpha}$
$\{(x_j,m_{x_j}),\ 1\le j\le k\}\subset \Xi^{\prime}\cap A^{\prime}_{x,m_x,r,\alpha}$
![]() $\big($
which ensures
$\big($
which ensures
![]() $A^{\prime}_{x_j,m_{x_j},r,\alpha}\subset A^{\prime}_{x,m_x,r,\alpha}\big)$
such that
$A^{\prime}_{x_j,m_{x_j},r,\alpha}\subset A^{\prime}_{x,m_x,r,\alpha}\big)$
such that
![]() $(x_k,m_{x_k})=(x,m)$
and
$(x_k,m_{x_k})=(x,m)$
and
for
![]() $1\le j\le k$
. Since
$1\le j\le k$
. Since
we can see that
![]() $\eta$
is range-bounded as in Definition 2.2 with
$\eta$
is range-bounded as in Definition 2.2 with
![]() $\bar{R}(x,\alpha)\,:\!=\,r\tan\!(\theta_1){+1}$
. The moment condition follows from the fact that
$\bar{R}(x,\alpha)\,:\!=\,r\tan\!(\theta_1){+1}$
. The moment condition follows from the fact that
![]() $\eta$
is bounded above by r. For the non-singularity, we extend
$\eta$
is bounded above by r. For the non-singularity, we extend
![]() $\Xi^{\prime}$
to
$\Xi^{\prime}$
to
![]() $\mathbb{R}^{d-1}\times[0,r]$
, write
$\mathbb{R}^{d-1}\times[0,r]$
, write
and let
![]() $(\Xi_{\Gamma_{\infty,r}^e})_j$
be the jth maximal layer of
$(\Xi_{\Gamma_{\infty,r}^e})_j$
be the jth maximal layer of
![]() $\Xi_{\Gamma_{\infty,r}^e}$
and
$\Xi_{\Gamma_{\infty,r}^e}$
and
![]() $\Xi^{\prime}_j=h((\Xi_{\Gamma_{\infty,r}^e})_j)$
. We can see that the corresponding unrestricted score function is
$\Xi^{\prime}_j=h((\Xi_{\Gamma_{\infty,r}^e})_j)$
. We can see that the corresponding unrestricted score function is
![]() $\bar{\eta}(x,\Xi^{\prime})=\sin\!(\theta_1)(r-m_x)\textbf{1}_{(x,m_x)\in \Xi^{\prime}_k}$
with the stabilising radius
$\bar{\eta}(x,\Xi^{\prime})=\sin\!(\theta_1)(r-m_x)\textbf{1}_{(x,m_x)\in \Xi^{\prime}_k}$
with the stabilising radius
![]() $R(x)=r\tan\!(\theta_1){+1}$
. Referring to Figure 8(b), we set
$R(x)=r\tan\!(\theta_1){+1}$
. Referring to Figure 8(b), we set
![]() $N_0\,:\!=\,\left(0,\frac{r\tan\!(\theta_1)}{2}\right)$
,
$N_0\,:\!=\,\left(0,\frac{r\tan\!(\theta_1)}{2}\right)$
,
![]() $B_0=\{(x,m);\,x\in N_0,0\le m\le x\cot\!(\theta_1)\}$
,
$B_0=\{(x,m);\,x\in N_0,0\le m\le x\cot\!(\theta_1)\}$
,
![]() $B_i$
as the triangle region with vertices
$B_i$
as the triangle region with vertices
 \begin{align*}&\left(r\tan\!(\theta_1)\left(\frac12+\frac{i-1}{4(k-1)}\right), r\!\left(\frac12+\frac{2i-1}{4(k-1)}\right)\right),\\&\left(r\tan\!(\theta_1)\left(\frac12+\frac{i}{4(k-1)}\right),r\!\left(\frac12+\frac{2i-1}{4(k-1)}\right)\right),\\&\left(r\tan\!(\theta_1)\left(\frac12+\frac{i}{4(k-1)}\right), r\!\left(\frac12+\frac{2i}{4(k-1)}\right)\right)\end{align*}
\begin{align*}&\left(r\tan\!(\theta_1)\left(\frac12+\frac{i-1}{4(k-1)}\right), r\!\left(\frac12+\frac{2i-1}{4(k-1)}\right)\right),\\&\left(r\tan\!(\theta_1)\left(\frac12+\frac{i}{4(k-1)}\right),r\!\left(\frac12+\frac{2i-1}{4(k-1)}\right)\right),\\&\left(r\tan\!(\theta_1)\left(\frac12+\frac{i}{4(k-1)}\right), r\!\left(\frac12+\frac{2i}{4(k-1)}\right)\right)\end{align*}
for
![]() $1\le i\le k-1$
, and
$1\le i\le k-1$
, and
Define
![]() $E\,:\!=\,\left\{\Xi^{\prime}\cap D=\emptyset, \left|\Xi^{\prime}\cap B_i\right|=1,1\le i\le k-1\right\}$
and
$E\,:\!=\,\left\{\Xi^{\prime}\cap D=\emptyset, \left|\Xi^{\prime}\cap B_i\right|=1,1\le i\le k-1\right\}$
and
![]() $E_0\,:\!=\,\big\{\big|\Xi^{\prime}_{N_0}\big|=\left|\Xi^{\prime}\cap B_0\right|=1\big\}$
. Then
$E_0\,:\!=\,\big\{\big|\Xi^{\prime}_{N_0}\big|=\left|\Xi^{\prime}\cap B_0\right|=1\big\}$
. Then
![]() $E\in\sigma\!\left(\Xi^{\prime}_{N_0^c}\right)$
,
$E\in\sigma\!\left(\Xi^{\prime}_{N_0^c}\right)$
,
![]() $\mathbb{P}(E)>0$
, and
$\mathbb{P}(E)>0$
, and
![]() $\mathbb{P}(E_0|E)>0$
. We can see that given E, the point in
$\mathbb{P}(E_0|E)>0$
. We can see that given E, the point in
![]() $\Xi^{\prime}\cap B_i$
is in
$\Xi^{\prime}\cap B_i$
is in
![]() $\Xi^{\prime}_{k-i}$
for all
$\Xi^{\prime}_{k-i}$
for all
![]() $1\le i\le k-1$
. Moreover, on
$1\le i\le k-1$
. Moreover, on
![]() $E\cap E_0$
, the point
$E\cap E_0$
, the point
![]() $({x_0},m_{x_0})$
in
$({x_0},m_{x_0})$
in
![]() $\Xi^{\prime}_{N_0}$
is in
$\Xi^{\prime}_{N_0}$
is in
![]() $\Xi^{\prime}_k.$
Hence, given E,
$\Xi^{\prime}_k.$
Hence, given E,
is non-singular.
As a final remark of the section, we mention that unrestricted versions of all the examples considered here can be proved, because it is trivial to show that the unrestricted version of the score function
![]() $\bar{\eta}$
satisfies the stabilisation condition in Definition 2.1 and the moment condition (2.3) using the same method, and the non-singularity in Assumption 2.4 for the restricted case is the same as that in the unrestricted case with the score function
$\bar{\eta}$
satisfies the stabilisation condition in Definition 2.1 and the moment condition (2.3) using the same method, and the non-singularity in Assumption 2.4 for the restricted case is the same as that in the unrestricted case with the score function
![]() $\bar{\eta}$
.
$\bar{\eta}$
.
4. Preliminaries and auxiliary results
We start with a few technical lemmas.
Lemma 4.1.
Assume
![]() $\xi_1,\dots,\xi_n$
are i.i.d. random variables having the triangular density function
$\xi_1,\dots,\xi_n$
are i.i.d. random variables having the triangular density function
 \begin{equation}\kappa_a(x)=\left\{\begin{array}{ll} \frac1a\left(1-\frac {|x|}a\right) & for\ |x|\le a,\\[4pt] 0 & for\ |x|>a, \end{array}\right.\end{equation}
\begin{equation}\kappa_a(x)=\left\{\begin{array}{ll} \frac1a\left(1-\frac {|x|}a\right) & for\ |x|\le a,\\[4pt] 0 & for\ |x|>a, \end{array}\right.\end{equation}
where
![]() $a>0$
. Let
$a>0$
. Let
![]() $T_n=\sum_{i=1}^n\xi_i$
. Then for any
$T_n=\sum_{i=1}^n\xi_i$
. Then for any
![]() $\gamma>0$
,
$\gamma>0$
,
 \begin{equation}d_{TV}(T_n,T_n+\gamma)\le \frac{\gamma}a\!\left\{\sqrt{\frac{3}{\pi n}}+\frac{2}{(2n-1)\pi^{2n}}\right\}.\end{equation}
\begin{equation}d_{TV}(T_n,T_n+\gamma)\le \frac{\gamma}a\!\left\{\sqrt{\frac{3}{\pi n}}+\frac{2}{(2n-1)\pi^{2n}}\right\}.\end{equation}
The following lemma says that if the distribution of a random variable is non-singular, then the distributions of random variables which are not far away from it are also non-singular.
Lemma 4.2.
Let F be a non-singular distribution on
![]() $\mathbb{R}$
with
$\mathbb{R}$
with
![]() $\alpha_F>0$
in the decomposition (1.1). If G is a distribution satisfying
$\alpha_F>0$
in the decomposition (1.1). If G is a distribution satisfying
![]() $d_{TV}\!\left(F, G\right)<\alpha_F$
, then the weight of the absolutely continuous component,
$d_{TV}\!\left(F, G\right)<\alpha_F$
, then the weight of the absolutely continuous component,
![]() $\alpha_G$
, in the Lebesgue decomposition of G,
$\alpha_G$
, in the Lebesgue decomposition of G,
satisfies
![]() $\alpha_G\ge \alpha_F-d_{TV}\!\left(F, G\right)$
.
$\alpha_G\ge \alpha_F-d_{TV}\!\left(F, G\right)$
.
We denote the convolution by
![]() $\ast$
.
$\ast$
.
Lemma 4.3.
For any two non-singular distributions
![]() $F_1$
and
$F_1$
and
![]() $F_2$
, there exist positive constants
$F_2$
, there exist positive constants
![]() $a>0$
,
$a>0$
,
![]() $u\in\mathbb{R}$
,
$u\in\mathbb{R}$
,
![]() $\theta\in (0,1]$
and a distribution function H such that
$\theta\in (0,1]$
and a distribution function H such that
where
![]() $K_a$
is the distribution of the triangle density
$K_a$
is the distribution of the triangle density
![]() $\kappa_a$
in (4.1), and
$\kappa_a$
in (4.1), and
![]() ${\delta}_u$
is the Dirac measure at u.
${\delta}_u$
is the Dirac measure at u.
Lemma 4.3 says that
![]() $F_1\ast F_2$
is the distribution function of
$F_1\ast F_2$
is the distribution function of
![]() $(X_1+u)X_3+X_2(1-X_3)$
, where
$(X_1+u)X_3+X_2(1-X_3)$
, where
![]() $X_1\sim K_a$
,
$X_1\sim K_a$
,
![]() $X_2\sim H$
,
$X_2\sim H$
,
![]() $X_3\sim{\textrm{Bernoulli}}(\theta)$
are independent random variables.
$X_3\sim{\textrm{Bernoulli}}(\theta)$
are independent random variables.
Remark 4.1. From the definition of the triangular density function, if a, u,
![]() $\theta$
satisfy (4.3) with a distribution H, then for arbitrary p, q such that
$\theta$
satisfy (4.3) with a distribution H, then for arbitrary p, q such that
![]() $0<q\le p\le 1$
, we can find an H
′ satisfying the equation with
$0<q\le p\le 1$
, we can find an H
′ satisfying the equation with
![]() $a^{\prime}=pa$
,
$a^{\prime}=pa$
,
![]() $u^{\prime}=u$
, and
$u^{\prime}=u$
, and
![]() $\theta^{\prime}=q\theta$
.
$\theta^{\prime}=q\theta$
.
Using the properties of the triangular distributions, we can derive that the sum of the score functions restricted by their radii of stabilisation has a similar property in Lemma 4.1 when the score function is range-bounded, exponentially stabilising, or polynomially stabilising with suitable
![]() $\beta$
.
$\beta$
.
Lemma 4.4.
Let
![]() $\Xi$
be a marked homogeneous Poisson point process on
$\Xi$
be a marked homogeneous Poisson point process on
![]() $(\mathbb{R}^d\times T,\mathscr{B}\big(\mathbb{R}^d\big)\times \mathscr{T})$
with intensity
$(\mathbb{R}^d\times T,\mathscr{B}\big(\mathbb{R}^d\big)\times \mathscr{T})$
with intensity
![]() $\lambda$
and i.i.d. marks in
$\lambda$
and i.i.d. marks in
![]() $(T,\mathscr{T})$
following
$(T,\mathscr{T})$
following
![]() $\mathscr{L}_{T}$
.
$\mathscr{L}_{T}$
.
-
(a) (Unrestricted case.) Assume that the score function
 $\eta$
satisfies the non-singularity in Assumption 2.4. If
$\eta$
satisfies the non-singularity in Assumption 2.4. If
 $\eta$
is polynomially stabilising as in Definition 2.1 with order
$\eta$
is polynomially stabilising as in Definition 2.1 with order
 $\beta>d+1$
, then (4.4)for any
$\beta>d+1$
, then (4.4)for any \begin{align} d_{TV}(W_{\alpha,r},W_{\alpha,r}+\gamma)&\le C\big(|\gamma|\vee 1\big)\left(\alpha^{-\frac{1}{2}}r^{\frac{d}{2}}\right) \end{align}
\begin{align} d_{TV}(W_{\alpha,r},W_{\alpha,r}+\gamma)&\le C\big(|\gamma|\vee 1\big)\left(\alpha^{-\frac{1}{2}}r^{\frac{d}{2}}\right) \end{align}
 $\gamma\in \mathbb{R}$
and
$\gamma\in \mathbb{R}$
and
 $r>R_0$
, where C and
$r>R_0$
, where C and
 $R_0$
are positive constants independent of
$R_0$
are positive constants independent of
 $\gamma$
. If
$\gamma$
. If
 $\eta$
is range-bounded as in Definition 2.1, then (4.5)for some positive constant C independent of
$\eta$
is range-bounded as in Definition 2.1, then (4.5)for some positive constant C independent of \begin{align}d_{TV}\big(W_\alpha, W_\alpha+\gamma\big)\le C(|\gamma|\vee 1)\alpha^{-\frac{1}{2}}\end{align}
\begin{align}d_{TV}\big(W_\alpha, W_\alpha+\gamma\big)\le C(|\gamma|\vee 1)\alpha^{-\frac{1}{2}}\end{align}
 $\gamma$
.
$\gamma$
.
-
(b) (Restricted case.) Assume that the score function
 $\eta$
satisfies the non-singularity in Assumption 2.4. If
$\eta$
satisfies the non-singularity in Assumption 2.4. If
 $\eta$
is polynomially stabilising as in Definition 2.2 with order
$\eta$
is polynomially stabilising as in Definition 2.2 with order
 $\beta>d+1$
, then (4.6)for any
$\beta>d+1$
, then (4.6)for any \begin{align} d_{TV}(\bar{W}_{\alpha,r},\bar{W}_{\alpha,r}+\gamma)&\le C(|\gamma|\vee 1)\left(\alpha^{-\frac{1}{2}}r^{\frac{d}{2}}\right) \end{align}
\begin{align} d_{TV}(\bar{W}_{\alpha,r},\bar{W}_{\alpha,r}+\gamma)&\le C(|\gamma|\vee 1)\left(\alpha^{-\frac{1}{2}}r^{\frac{d}{2}}\right) \end{align}
 $\gamma\in \mathbb{R}$
and
$\gamma\in \mathbb{R}$
and
 $r>R_0$
, where C and
$r>R_0$
, where C and
 $R_0$
are positive constants independent of
$R_0$
are positive constants independent of
 $\gamma$
. If
$\gamma$
. If
 $\eta$
is range-bounded as in Definition 2.2, then (4.7)for some positive constant C independent of
$\eta$
is range-bounded as in Definition 2.2, then (4.7)for some positive constant C independent of \begin{align}d_{TV}(\bar{W}_\alpha,\bar{W}_\alpha+\gamma)\le C(|\gamma|\vee 1)\alpha^{-\frac{1}{2}}\end{align}
\begin{align}d_{TV}(\bar{W}_\alpha,\bar{W}_\alpha+\gamma)\le C(|\gamma|\vee 1)\alpha^{-\frac{1}{2}}\end{align}
 $\gamma$
.
$\gamma$
.
Remark 4.2. Since exponential stabilisation implies polynomial stabilisation, the statements (4.4) and (4.6) also hold under the corresponding exponential stabilisation conditions.
We can generalise Lemma 4.4 by replacing
![]() $\gamma$
with a function of
$\gamma$
with a function of
![]() $\Xi_N$
for some Borel set N and the expectation with a conditional expectation.
$\Xi_N$
for some Borel set N and the expectation with a conditional expectation.
Corollary 4.1.
For
![]() $\alpha,r>0$
, let
$\alpha,r>0$
, let
![]() $\big\{N_{\alpha,r}^{(k)}\big\}_{k\in\{1,2,3\}}\subset\mathscr{B}\big(\mathbb{R}^d\big)$
be such that
$\big\{N_{\alpha,r}^{(k)}\big\}_{k\in\{1,2,3\}}\subset\mathscr{B}\big(\mathbb{R}^d\big)$
be such that
for a point
![]() $x\in \mathbb{R}^d$
and a positive constant
$x\in \mathbb{R}^d$
and a positive constant
![]() $q\in \big(0,\frac{1}{2}\big)$
, let
$q\in \big(0,\frac{1}{2}\big)$
, let
![]() $\mathscr{F}_{0,\alpha,r}$
be a sub-
$\mathscr{F}_{0,\alpha,r}$
be a sub-
![]() $\sigma$
-algebra of
$\sigma$
-algebra of
![]() $\sigma\!\left(\Xi_{N_{\alpha,r}^{(1)}}\right)$
, and let
$\sigma\!\left(\Xi_{N_{\alpha,r}^{(1)}}\right)$
, and let
![]() $h_{\alpha,r}$
be a measurable function mapping configurations on
$h_{\alpha,r}$
be a measurable function mapping configurations on
![]() $N_{\alpha, r}^{(2)}\times T$
to the real space.
$N_{\alpha, r}^{(2)}\times T$
to the real space.
-
(a) (Unrestricted case.) Define
If the conditions of Lemma 4.4(a) hold, then \begin{equation*}W^{\prime}_{\alpha,r}\,:\!=\,\sum_{(x,m)\in \Xi_{\Gamma_\alpha\backslash N_{\alpha,r}^{(3)}}}\eta(\left(x,m\right)\!, \Xi)\textbf{1}_{R(x)\le r}.\end{equation*}
(4.8)for
\begin{equation*}W^{\prime}_{\alpha,r}\,:\!=\,\sum_{(x,m)\in \Xi_{\Gamma_\alpha\backslash N_{\alpha,r}^{(3)}}}\eta(\left(x,m\right)\!, \Xi)\textbf{1}_{R(x)\le r}.\end{equation*}
(4.8)for \begin{align} &d_{TV}\!\left(W^{\prime}_{\alpha,r},W^{\prime}_{\alpha,r}+h_{\alpha,r}\left(\Xi_{N_{\alpha, r}^{(2)}}\right)\middle|\mathscr{F}_{0,\alpha,r}\right) \nonumber\\ &\le \mathbb{E}\!\left(\left|h_{\alpha,r}\left(\Xi_{N_{\alpha, r}^{(2)}}\right)\right|\vee 1\middle|\mathscr{F}_{0,\alpha,r} \right)\mathop{{}\textrm{O}}\mathopen{}\left(\alpha^{-\frac{1}{2}}r^{\frac{d}{2}}\right)a.s. \end{align}
\begin{align} &d_{TV}\!\left(W^{\prime}_{\alpha,r},W^{\prime}_{\alpha,r}+h_{\alpha,r}\left(\Xi_{N_{\alpha, r}^{(2)}}\right)\middle|\mathscr{F}_{0,\alpha,r}\right) \nonumber\\ &\le \mathbb{E}\!\left(\left|h_{\alpha,r}\left(\Xi_{N_{\alpha, r}^{(2)}}\right)\right|\vee 1\middle|\mathscr{F}_{0,\alpha,r} \right)\mathop{{}\textrm{O}}\mathopen{}\left(\alpha^{-\frac{1}{2}}r^{\frac{d}{2}}\right)a.s. \end{align}
 $r>R_0$
, where
$r>R_0$
, where
 $R_0>0$
is a constant, and
$R_0>0$
is a constant, and
 $\mathop{{}\textrm{O}}\mathopen{}\left(\alpha^{-\frac{1}{2}}r^{\frac{d}{2}}\right)$
is independent of the sets
$\mathop{{}\textrm{O}}\mathopen{}\left(\alpha^{-\frac{1}{2}}r^{\frac{d}{2}}\right)$
is independent of the sets
 $\big\{N_{\alpha,r}^{(k)}\big\}_{\alpha,r\in \mathbb{R}_+,k\in\{1,2,3\}}$
, functions
$\big\{N_{\alpha,r}^{(k)}\big\}_{\alpha,r\in \mathbb{R}_+,k\in\{1,2,3\}}$
, functions
 $\{h_{\alpha,r}\}_{\alpha,r\in \mathbb{R}_+}$
and
$\{h_{\alpha,r}\}_{\alpha,r\in \mathbb{R}_+}$
and
 $\sigma$
-algebras
$\sigma$
-algebras
 $\{\mathscr{F}_{0,\alpha,r}\}_{\alpha,r\in \mathbb{R}_+}$
.
$\{\mathscr{F}_{0,\alpha,r}\}_{\alpha,r\in \mathbb{R}_+}$
.
-
(b) (Restricted case.) Define
If the conditions of Lemma 4.4(b) hold, then \begin{equation*}\bar{W}^{\prime}_{\alpha,r}\,:\!=\,\sum_{(x,m)\in \Xi_{\Gamma_\alpha\backslash N_{\alpha,r}^{(3)}}}\eta(\left(x,m\right)\!, \Xi,{\Gamma_\alpha})\textbf{1}_{\bar{R}(x,\alpha)<r}.\end{equation*}
(4.9)for
\begin{equation*}\bar{W}^{\prime}_{\alpha,r}\,:\!=\,\sum_{(x,m)\in \Xi_{\Gamma_\alpha\backslash N_{\alpha,r}^{(3)}}}\eta(\left(x,m\right)\!, \Xi,{\Gamma_\alpha})\textbf{1}_{\bar{R}(x,\alpha)<r}.\end{equation*}
(4.9)for \begin{align} &d_{TV}\!\left(\bar{W}^{\prime}_{\alpha,r},\bar{W}^{\prime}_{\alpha,r}+h_{\alpha,r}\left(\Xi_{N_{\alpha, r}^{(2)} }\right)\middle|\mathscr{F}_{0,\alpha,r}\right)\nonumber\\ &\le \mathbb{E}\!\left(\left|h_{\alpha,r}\left(\Xi_{N_{\alpha, r}^{(2)} }\right)\right|\vee 1\middle|\mathscr{F}_{0,\alpha,r} \right)\mathop{{}\textrm{O}}\mathopen{}\left(\alpha^{-\frac{1}{2}}r^{\frac{d}{2}}\right)a.s. \end{align}
\begin{align} &d_{TV}\!\left(\bar{W}^{\prime}_{\alpha,r},\bar{W}^{\prime}_{\alpha,r}+h_{\alpha,r}\left(\Xi_{N_{\alpha, r}^{(2)} }\right)\middle|\mathscr{F}_{0,\alpha,r}\right)\nonumber\\ &\le \mathbb{E}\!\left(\left|h_{\alpha,r}\left(\Xi_{N_{\alpha, r}^{(2)} }\right)\right|\vee 1\middle|\mathscr{F}_{0,\alpha,r} \right)\mathop{{}\textrm{O}}\mathopen{}\left(\alpha^{-\frac{1}{2}}r^{\frac{d}{2}}\right)a.s. \end{align}
 $r>R_0$
, where
$r>R_0$
, where
 $R_0>0$
is a constant, and
$R_0>0$
is a constant, and
 $\mathop{{}\textrm{O}}\mathopen{}\left(\alpha^{-\frac{1}{2}}r^{\frac{d}{2}}\right)$
is independent of the sets
$\mathop{{}\textrm{O}}\mathopen{}\left(\alpha^{-\frac{1}{2}}r^{\frac{d}{2}}\right)$
is independent of the sets
 $\big\{N_{\alpha,r}^{(k)}\big\}_{\alpha,r\in \mathbb{R}_+,k\in\{1,2,3\}}$
, functions
$\big\{N_{\alpha,r}^{(k)}\big\}_{\alpha,r\in \mathbb{R}_+,k\in\{1,2,3\}}$
, functions
 $\{h_{\alpha,r}\}_{\alpha,r\in \mathbb{R}_+}$
and
$\{h_{\alpha,r}\}_{\alpha,r\in \mathbb{R}_+}$
and
 $\sigma$
-algebras
$\sigma$
-algebras
 $\{\mathscr{F}_{0,\alpha,r}\}_{\alpha,r\in \mathbb{R}_+}$
.
$\{\mathscr{F}_{0,\alpha,r}\}_{\alpha,r\in \mathbb{R}_+}$
.
As discussed in the motivating example, the orders of
![]() ${\textrm{Var}}\!\left(W_{\alpha}\right)$
and
${\textrm{Var}}\!\left(W_{\alpha}\right)$
and
![]() ${\textrm{Var}}\!\left(\bar{W}_{\alpha}\right)$
play a pivotal role in the accuracy of the normal approximation. The next lemma says that the optimal order of the variance can be achieved under exponential stabilisation.
${\textrm{Var}}\!\left(\bar{W}_{\alpha}\right)$
play a pivotal role in the accuracy of the normal approximation. The next lemma says that the optimal order of the variance can be achieved under exponential stabilisation.
Lemma 4.5.
-
(a) (Unrestricted case.) If the score function
 $\eta$
satisfies the third moment condition (2.3), the non-singularity in Assumption 2.4, and the exponential stabilisation in Definition 2.1, then
$\eta$
satisfies the third moment condition (2.3), the non-singularity in Assumption 2.4, and the exponential stabilisation in Definition 2.1, then
 ${\textrm{Var}}\!\left(W_{\alpha}\right)=\Omega\!\left(\alpha\right)$
.
${\textrm{Var}}\!\left(W_{\alpha}\right)=\Omega\!\left(\alpha\right)$
. -
(b) (Restricted case.) If the score function
 $\eta$
satisfies the third moment condition (2.4), the non-singularity in Assumption 2.4, and the exponential stabilisation in Definition 2.2, then
$\eta$
satisfies the third moment condition (2.4), the non-singularity in Assumption 2.4, and the exponential stabilisation in Definition 2.2, then
 ${\textrm{Var}}\!\left(\bar{W}_{\alpha}\right)$
${\textrm{Var}}\!\left(\bar{W}_{\alpha}\right)$
 $=\Omega\!\left(\alpha\right)$
.
$=\Omega\!\left(\alpha\right)$
.
We cannot obtain the optimal order of the variances in the polynomially stabilising case, but the following lower bound can be established.
Lemma 4.6.
-
(a) (Unrestricted case.) If the score function
 $\eta$
satisfies the k′th moment condition (2.3) with
$\eta$
satisfies the k′th moment condition (2.3) with
 $k^{\prime}>k\ge3$
and the non-singularity in Assumption 2.4, and is polynomially stabilising as in Definition 2.1 with parameter
$k^{\prime}>k\ge3$
and the non-singularity in Assumption 2.4, and is polynomially stabilising as in Definition 2.1 with parameter
 $\beta>(3k-2)d/(k-2)$
, then
$\beta>(3k-2)d/(k-2)$
, then  \begin{equation*}{\textrm{Var}}\!\left(W_{\alpha}\right)\ge \mathop{{}\textrm{O}}\mathopen{}\left(\alpha^{\frac{k\beta-2\beta-3dk+2d}{k\beta-2\beta-dk}}\right).\end{equation*}
\begin{equation*}{\textrm{Var}}\!\left(W_{\alpha}\right)\ge \mathop{{}\textrm{O}}\mathopen{}\left(\alpha^{\frac{k\beta-2\beta-3dk+2d}{k\beta-2\beta-dk}}\right).\end{equation*}
-
(b) (Restricted case.) If the score function
 $\eta$
satisfies the k′th moment condition (2.4) with
$\eta$
satisfies the k′th moment condition (2.4) with
 $k^{\prime}>k\ge3$
and the non-singularity in Assumption 2.4, and is polynomially stabilising as in Definition 2.2 with parameter
$k^{\prime}>k\ge3$
and the non-singularity in Assumption 2.4, and is polynomially stabilising as in Definition 2.2 with parameter
 $\beta>(3k-2)d/(k-2)$
, then
$\beta>(3k-2)d/(k-2)$
, then  \begin{equation*}{\textrm{Var}}\!\left(\bar{W}_{\alpha}\right)\ge \mathop{{}\textrm{O}}\mathopen{}\left(\alpha^{\frac{k\beta-2\beta-3dk+2d}{k\beta-2\beta-dk}}\right).\end{equation*}
\begin{equation*}{\textrm{Var}}\!\left(\bar{W}_{\alpha}\right)\ge \mathop{{}\textrm{O}}\mathopen{}\left(\alpha^{\frac{k\beta-2\beta-3dk+2d}{k\beta-2\beta-dk}}\right).\end{equation*}
5. The proofs of the auxiliary and main results
We need Palm processes and reduced Palm processes in our proofs, and for ease of reading, we briefly recall their definitions. Let E be a Polish space with Borel
![]() $\sigma$
-algebra
$\sigma$
-algebra
![]() $\mathscr{E}$
and configuration space
$\mathscr{E}$
and configuration space
![]() $\left(\boldsymbol{C}_E, \mathscr{C}_E\right)$
, let
$\left(\boldsymbol{C}_E, \mathscr{C}_E\right)$
, let
![]() $\Psi$
be a point process on
$\Psi$
be a point process on
![]() $\left(E, \mathscr{E}\right)$
, and write the mean measure of
$\left(E, \mathscr{E}\right)$
, and write the mean measure of
![]() $\Psi$
as
$\Psi$
as
![]() $\psi (d x) \,:\!=\, \mathbb{E} \Psi (d x)$
. The family of point processes
$\psi (d x) \,:\!=\, \mathbb{E} \Psi (d x)$
. The family of point processes
![]() $\{ \Psi_x \,:\, x \in E\}$
are said to be the Palm processes associated with
$\{ \Psi_x \,:\, x \in E\}$
are said to be the Palm processes associated with
![]() $\Psi$
if for any measurable function
$\Psi$
if for any measurable function
![]() $f \,:\, E\times \boldsymbol{C}_E \rightarrow [0,\infty)$
,
$f \,:\, E\times \boldsymbol{C}_E \rightarrow [0,\infty)$
,
see [Reference Kallenberg26, Section 10.1]. A Palm process
![]() $\Psi_x$
contains a point at x, and it is often more convenient to consider the reduced Palm process
$\Psi_x$
contains a point at x, and it is often more convenient to consider the reduced Palm process
![]() $\Psi_x-\delta_x$
at x by removing the point x from
$\Psi_x-\delta_x$
at x by removing the point x from
![]() $\Psi_x$
. Furthermore, suppose that the factorial moments
$\Psi_x$
. Furthermore, suppose that the factorial moments
are locally finite; then we can respectively define the second-order Palm processes
![]() $\{ \Psi_{xy}\,:\, x,y \in E \}$
and third-order Palm processes
$\{ \Psi_{xy}\,:\, x,y \in E \}$
and third-order Palm processes
![]() $\{ \Psi_{xyz}\,:\, x,y,z \in E \}$
associated with
$\{ \Psi_{xyz}\,:\, x,y,z \in E \}$
associated with
![]() $\Psi$
by
$\Psi$
by
 \begin{align} &\mathbb{E} \!\left[ \iint\limits_{E^2} f(x,y;\,\Psi)\Psi(dx)(\Psi-{\delta}_x)(dy) \right]= \iint\limits_{E^2} \mathbb{E} f(x,y;\,\Psi_{xy}) \psi^{[2]} (dx,dy) ,\\ &\mathbb{E} \!\left[ \iiint\limits_{E^3} f(x,y,z;\,\Psi)\Psi(dx)(\Psi-{\delta}_x)(dy)(\Psi-{\delta}_x-{\delta}_y)(dz) \right] \nonumber\end{align}
\begin{align} &\mathbb{E} \!\left[ \iint\limits_{E^2} f(x,y;\,\Psi)\Psi(dx)(\Psi-{\delta}_x)(dy) \right]= \iint\limits_{E^2} \mathbb{E} f(x,y;\,\Psi_{xy}) \psi^{[2]} (dx,dy) ,\\ &\mathbb{E} \!\left[ \iiint\limits_{E^3} f(x,y,z;\,\Psi)\Psi(dx)(\Psi-{\delta}_x)(dy)(\Psi-{\delta}_x-{\delta}_y)(dz) \right] \nonumber\end{align}
for all measurable functions
![]() $f \,:\, E^2 \times \boldsymbol{C}_E \rightarrow [0,\infty)$
in (5.2) and
$f \,:\, E^2 \times \boldsymbol{C}_E \rightarrow [0,\infty)$
in (5.2) and
![]() $f: E^3 \times \boldsymbol{C}_E \rightarrow [0,\infty)$
in (5.3) [Reference Kallenberg26, Section 12.3]. Using reduced Palm processes, the Slivnyak–Mecke theorem [Reference Mecke35] states that the distributions of the reduced Palm processes of a point process are the same as that of the point process if and only if the point process is a Poisson point process. Then we can see that for a homogeneous Poisson point process with rate
$f: E^3 \times \boldsymbol{C}_E \rightarrow [0,\infty)$
in (5.3) [Reference Kallenberg26, Section 12.3]. Using reduced Palm processes, the Slivnyak–Mecke theorem [Reference Mecke35] states that the distributions of the reduced Palm processes of a point process are the same as that of the point process if and only if the point process is a Poisson point process. Then we can see that for a homogeneous Poisson point process with rate
![]() $\lambda$
, its mean measure can be written as
$\lambda$
, its mean measure can be written as
![]() $\Lambda(dx)=\lambda dx$
; its Palm processes satisfy
$\Lambda(dx)=\lambda dx$
; its Palm processes satisfy
![]() $\Psi_{x}\overset{d}{=}\Psi+{\delta}_x$
,
$\Psi_{x}\overset{d}{=}\Psi+{\delta}_x$
,
![]() $\Psi_{xy}\overset{d}{=}\Psi+{\delta}_x+{\delta}_y$
, and
$\Psi_{xy}\overset{d}{=}\Psi+{\delta}_x+{\delta}_y$
, and
![]() $\Psi_{xyz}\overset{d}{=}\Psi+{\delta}_x+{\delta}_y+{\delta}_z$
; and the factorial moments
$\Psi_{xyz}\overset{d}{=}\Psi+{\delta}_x+{\delta}_y+{\delta}_z$
; and the factorial moments
![]() $\psi^{[2]}(dx,dy)=\lambda^2dxdy$
and
$\psi^{[2]}(dx,dy)=\lambda^2dxdy$
and
![]() $\psi^{[3]}(dx,dy,dz)=\lambda^3dxdydz$
for all distinct x, y,
$\psi^{[3]}(dx,dy,dz)=\lambda^3dxdydz$
for all distinct x, y,
![]() $z\in E=\mathbb{R}^d$
.
$z\in E=\mathbb{R}^d$
.
We can adapt (5.1), (5.2), and (5.3) to the marked point process
![]() $\Xi$
. To this end, we assume that the rate of
$\Xi$
. To this end, we assume that the rate of
![]() $\bar{\Xi}$
is
$\bar{\Xi}$
is
![]() $\lambda$
, and that
$\lambda$
, and that
![]() $\{M_i\}_{1\le i\le 3}$
are i.i.d. random elements on
$\{M_i\}_{1\le i\le 3}$
are i.i.d. random elements on
![]() $(T,\mathscr{T})$
following the distribution
$(T,\mathscr{T})$
following the distribution
![]() $\mathscr{L}_{T}$
, which are independent of
$\mathscr{L}_{T}$
, which are independent of
![]() $\Xi$
. We use
$\Xi$
. We use
![]() $M_x$
to denote the mark of x if
$M_x$
to denote the mark of x if
![]() $x\in \bar{\Xi}$
. Because of the independence of the marks, we can obtain the following corollaries of the Campbell–Mecke theorem (also known as the Mecke equation) and the multivariate Mecke equation [Reference Chiu, Stoyan, Kendall and Mecke15, p. 130]:
$x\in \bar{\Xi}$
. Because of the independence of the marks, we can obtain the following corollaries of the Campbell–Mecke theorem (also known as the Mecke equation) and the multivariate Mecke equation [Reference Chiu, Stoyan, Kendall and Mecke15, p. 130]:
 \begin{align} &\mathbb{E} \!\left[ \int_{\mathbb{R}^d} f((x,M_x),\Xi)\bar{\Xi}(dx) \right] = \int_{\mathbb{R}^d} \mathbb{E} f((x,M_1),\Xi+{\delta}_{(x,M_1)}) \lambda dx, \\ &\mathbb{E} \!\left[ \iint\limits_{\ \left(\mathbb{R}^d\right)^2} f((x,M_x),(y,M_y);\,\Xi)\bar{\Xi}(dx)(\bar{\Xi}-{\delta}_x)(dy) \right] \nonumber \end{align}
\begin{align} &\mathbb{E} \!\left[ \int_{\mathbb{R}^d} f((x,M_x),\Xi)\bar{\Xi}(dx) \right] = \int_{\mathbb{R}^d} \mathbb{E} f((x,M_1),\Xi+{\delta}_{(x,M_1)}) \lambda dx, \\ &\mathbb{E} \!\left[ \iint\limits_{\ \left(\mathbb{R}^d\right)^2} f((x,M_x),(y,M_y);\,\Xi)\bar{\Xi}(dx)(\bar{\Xi}-{\delta}_x)(dy) \right] \nonumber \end{align}
 \begin{align} = \iint\limits_{\left(\mathbb{R}^d\right)^2} \mathbb{E} f((x,M_1),(y,M_2);\,\Xi+{\delta}_{(x,M_1)}+{\delta}_{(y,M_2)}) \lambda^2dxdy ,\qquad\qquad\end{align}
\begin{align} = \iint\limits_{\left(\mathbb{R}^d\right)^2} \mathbb{E} f((x,M_1),(y,M_2);\,\Xi+{\delta}_{(x,M_1)}+{\delta}_{(y,M_2)}) \lambda^2dxdy ,\qquad\qquad\end{align}
 \begin{align} &\mathbb{E} \!\left[ \iiint\limits_{\left(\mathbb{R}^d\right)^3} f((x,M_x),(y,M_y),(z,M_z);\,\Xi)\bar{\Xi}(dx)(\bar{\Xi}-{\delta}_x)(dy)(\bar{\Xi}-{\delta}_x-{\delta}_y)(dz) \right]\nonumber \\ =& \iiint\limits_{\left(\mathbb{R}^d\right)^3} \mathbb{E} f((x,M_1),(y,M_2),(z,M_3);\,\Xi+{\delta}_{(x,M_1)}+{\delta}_{(y,M_2)}+{\delta}_{(z,M_3)}) \lambda^3dxdydz,\end{align}
\begin{align} &\mathbb{E} \!\left[ \iiint\limits_{\left(\mathbb{R}^d\right)^3} f((x,M_x),(y,M_y),(z,M_z);\,\Xi)\bar{\Xi}(dx)(\bar{\Xi}-{\delta}_x)(dy)(\bar{\Xi}-{\delta}_x-{\delta}_y)(dz) \right]\nonumber \\ =& \iiint\limits_{\left(\mathbb{R}^d\right)^3} \mathbb{E} f((x,M_1),(y,M_2),(z,M_3);\,\Xi+{\delta}_{(x,M_1)}+{\delta}_{(y,M_2)}+{\delta}_{(z,M_3)}) \lambda^3dxdydz,\end{align}
for all measurable functions
![]() $f \,:\,\boldsymbol{S} \times \boldsymbol{C}_{\boldsymbol{S}} \rightarrow [0,\infty)$
in (5.4),
$f \,:\,\boldsymbol{S} \times \boldsymbol{C}_{\boldsymbol{S}} \rightarrow [0,\infty)$
in (5.4),
![]() $f\,:\,\boldsymbol{S}^2 \times\boldsymbol{C}_{\boldsymbol{S}} \rightarrow [0,\infty)$
in (5.5), and
$f\,:\,\boldsymbol{S}^2 \times\boldsymbol{C}_{\boldsymbol{S}} \rightarrow [0,\infty)$
in (5.5), and
![]() $f\,:\,\boldsymbol{S}^3 \times \boldsymbol{C}_{\boldsymbol{S}} \rightarrow [0,\infty)$
in (5.6).
$f\,:\,\boldsymbol{S}^3 \times \boldsymbol{C}_{\boldsymbol{S}} \rightarrow [0,\infty)$
in (5.6).
Recalling the shift operator defined in Section 2, we can write
![]() $g(\mathscr{X}^x)\,:\!=\,\eta(\left(x,m\right)\!, \mathscr{X}\,)$
(resp.
$g(\mathscr{X}^x)\,:\!=\,\eta(\left(x,m\right)\!, \mathscr{X}\,)$
(resp.
![]() $g_\alpha(x,\mathscr{X}\,)\,:\!=\, \eta\!\left(\left(x,m\right)\!,\Xi,\mathscr{X},\Gamma_\alpha\right)$
) for every configuration
$g_\alpha(x,\mathscr{X}\,)\,:\!=\, \eta\!\left(\left(x,m\right)\!,\Xi,\mathscr{X},\Gamma_\alpha\right)$
) for every configuration
![]() $\mathscr{X}$
,
$\mathscr{X}$
,
![]() $(x,m)\in \mathscr{X}$
, and
$(x,m)\in \mathscr{X}$
, and
![]() $\alpha>0$
, so that the notation can be simplified significantly; e.g.,
$\alpha>0$
, so that the notation can be simplified significantly; e.g.,
 \begin{eqnarray*} W_\alpha&=&\sum_{(x,m)\in\Xi_{\Gamma_\alpha}}\eta(\left(x,m\right)\!, \Xi)=\int_{\Gamma_\alpha} g(\Xi^x)\bar{\Xi}(dx)=\sum_{x\in \bar{\Xi}}g(\Xi^x),\\ \bar{W}_\alpha&=&\sum_{(x,m)\in\Xi_{\Gamma_\alpha}}\eta(\left(x,m\right)\!, \Xi,\Gamma_\alpha)=\int_{\Gamma_\alpha}{g_\alpha(x, {\Xi})\bar{\Xi}(dx)},\end{eqnarray*}
\begin{eqnarray*} W_\alpha&=&\sum_{(x,m)\in\Xi_{\Gamma_\alpha}}\eta(\left(x,m\right)\!, \Xi)=\int_{\Gamma_\alpha} g(\Xi^x)\bar{\Xi}(dx)=\sum_{x\in \bar{\Xi}}g(\Xi^x),\\ \bar{W}_\alpha&=&\sum_{(x,m)\in\Xi_{\Gamma_\alpha}}\eta(\left(x,m\right)\!, \Xi,\Gamma_\alpha)=\int_{\Gamma_\alpha}{g_\alpha(x, {\Xi})\bar{\Xi}(dx)},\end{eqnarray*}
where
![]() $\bar{\Xi}$
is the projection of
$\bar{\Xi}$
is the projection of
![]() $\Xi$
on
$\Xi$
on
![]() $\mathbb{R}^d$
, and R and
$\mathbb{R}^d$
, and R and
![]() $\bar{R}(x,\alpha)$
are the corresponding radii of stabilisation. Here,
$\bar{R}(x,\alpha)$
are the corresponding radii of stabilisation. Here,
![]() $g(\mathscr{X}\,)$
(resp.
$g(\mathscr{X}\,)$
(resp.
![]() $g_\alpha(x,\mathscr{X}\,)$
) is not affected by m since
$g_\alpha(x,\mathscr{X}\,)$
) is not affected by m since
![]() $\eta\!\left((x,m),\mathscr{X}\right)$
(resp.
$\eta\!\left((x,m),\mathscr{X}\right)$
(resp.
![]() $\eta\!\left(\left(x,m\right)\!,\Xi,\mathscr{X},\Gamma_\alpha\right)$
) is understood as 0 if
$\eta\!\left(\left(x,m\right)\!,\Xi,\mathscr{X},\Gamma_\alpha\right)$
) is understood as 0 if
![]() $(x,m)\notin \mathscr{X}$
.
$(x,m)\notin \mathscr{X}$
.
Since the mean and variance of
![]() $\bar{W}_{\alpha}$
are generally different from those of
$\bar{W}_{\alpha}$
are generally different from those of
![]() $\bar{W}_{\alpha,r}$
, in the proof of Theorem 2.2, we will need the bound of the total variation distance between two normal distributions.
$\bar{W}_{\alpha,r}$
, in the proof of Theorem 2.2, we will need the bound of the total variation distance between two normal distributions.
Lemma 5.1. ([Reference Devroye, Mehrabian and Redded18, Theorem 1.3].) Let
![]() $F_{\mu,\sigma}$
be the distribution of
$F_{\mu,\sigma}$
be the distribution of
![]() $N(\mu,\sigma^2)$
; then
$N(\mu,\sigma^2)$
; then
To find suitable normal approximations for
![]() $W_{\alpha}$
and
$W_{\alpha}$
and
![]() $W_{\alpha,r}$
(resp.
$W_{\alpha,r}$
(resp.
![]() $\bar{W}_{\alpha}$
and
$\bar{W}_{\alpha}$
and
![]() $\bar{W}_{\alpha,r}$
), we need to analyse the first two moments of
$\bar{W}_{\alpha,r}$
), we need to analyse the first two moments of
![]() $W_{\alpha}$
and
$W_{\alpha}$
and
![]() $W_{\alpha,r}$
(resp.
$W_{\alpha,r}$
(resp.
![]() $\bar{W}_{\alpha}$
and
$\bar{W}_{\alpha}$
and
![]() $\bar{W}_{\alpha,r}$
). Before doing this, we establish a few lemmas needed in the proofs.
$\bar{W}_{\alpha,r}$
). Before doing this, we establish a few lemmas needed in the proofs.
Lemma 5.2. (Conditional total variance formula.) Let X be a random variable on the probability space
![]() $(\Omega, \mathscr{G},\mathbb{P})$
with a finite second moment, and let
$(\Omega, \mathscr{G},\mathbb{P})$
with a finite second moment, and let
![]() $\mathscr{G}_1$
and
$\mathscr{G}_1$
and
![]() $\mathscr{G}_2$
be two sub-
$\mathscr{G}_2$
be two sub-
![]() $\sigma$
-algebras of
$\sigma$
-algebras of
![]() $\mathscr{G}$
such that
$\mathscr{G}$
such that
![]() $\mathscr{G}_1\subset \mathscr{G}_2$
. Then
$\mathscr{G}_1\subset \mathscr{G}_2$
. Then
Proof. From the definition of the conditional variance, we can see that
 \begin{align*} {\textrm{Var}}\!\left(X|\mathscr{G}_1\right)&=\mathbb{E}\!\left(X^2\middle|\mathscr{G}_1\right)-\mathbb{E}\!\left(X\middle|\mathscr{G}_1\right)^2 \\&=\mathbb{E}\!\left(\mathbb{E}\!\left(X^2\middle|\mathscr{G}_2\right)\middle|\mathscr{G}_1\right)-\mathbb{E}\!\left(\mathbb{E}\!\left(X\middle|\mathscr{G}_2\right)\middle|\mathscr{G}_1\right)^2 \\&=\mathbb{E}\!\left(\mathbb{E}\!\left(X^2\middle|\mathscr{G}_2\right)\middle|\mathscr{G}_1\right)-\mathbb{E}\!\left(\mathbb{E}\!\left(X\middle|\mathscr{G}_2\right)^2\middle|\mathscr{G}_1\right)+\mathbb{E}\!\left(\mathbb{E}\!\left(X\middle|\mathscr{G}_2\right)^2\middle|\mathscr{G}_1\right)\\ &\quad -\mathbb{E}\!\left(\mathbb{E}\!\left(X\middle|\mathscr{G}_2\right)\middle|\mathscr{G}_1\right)^2 \\&=\mathbb{E}\!\left({\textrm{Var}}\!\left(X\middle|\mathscr{G}_2\right)\middle|\mathscr{G}_1\right)+{\textrm{Var}}\!\left(\mathbb{E}\!\left(X\middle|\mathscr{G}_2\right)\middle|\mathscr{G}_1\right),\end{align*}
\begin{align*} {\textrm{Var}}\!\left(X|\mathscr{G}_1\right)&=\mathbb{E}\!\left(X^2\middle|\mathscr{G}_1\right)-\mathbb{E}\!\left(X\middle|\mathscr{G}_1\right)^2 \\&=\mathbb{E}\!\left(\mathbb{E}\!\left(X^2\middle|\mathscr{G}_2\right)\middle|\mathscr{G}_1\right)-\mathbb{E}\!\left(\mathbb{E}\!\left(X\middle|\mathscr{G}_2\right)\middle|\mathscr{G}_1\right)^2 \\&=\mathbb{E}\!\left(\mathbb{E}\!\left(X^2\middle|\mathscr{G}_2\right)\middle|\mathscr{G}_1\right)-\mathbb{E}\!\left(\mathbb{E}\!\left(X\middle|\mathscr{G}_2\right)^2\middle|\mathscr{G}_1\right)+\mathbb{E}\!\left(\mathbb{E}\!\left(X\middle|\mathscr{G}_2\right)^2\middle|\mathscr{G}_1\right)\\ &\quad -\mathbb{E}\!\left(\mathbb{E}\!\left(X\middle|\mathscr{G}_2\right)\middle|\mathscr{G}_1\right)^2 \\&=\mathbb{E}\!\left({\textrm{Var}}\!\left(X\middle|\mathscr{G}_2\right)\middle|\mathscr{G}_1\right)+{\textrm{Var}}\!\left(\mathbb{E}\!\left(X\middle|\mathscr{G}_2\right)\middle|\mathscr{G}_1\right),\end{align*}
so the statement holds.
Also, given the value of a random variable in a certain event, we can find a lower bound for the conditional variance.
Lemma 5.3.
Let X be a random variable on the probability space
![]() $(\Omega, \mathscr{G},\mathbb{P})$
with a finite second moment. For any event A and
$(\Omega, \mathscr{G},\mathbb{P})$
with a finite second moment. For any event A and
![]() $\sigma$
-algebra such that
$\sigma$
-algebra such that
![]() $\mathscr{F}\subset\mathscr{G}$
,
$\mathscr{F}\subset\mathscr{G}$
,
where
![]() $\frac{0}{0}=0$
by convention.
$\frac{0}{0}=0$
by convention.
Proof of Lemma
5.3. The statement is trivially true if
![]() $\mathbb{P} (A)=0$
, so we focus on the case that
$\mathbb{P} (A)=0$
, so we focus on the case that
![]() $\mathbb{P}(A)>0$
. Let
$\mathbb{P}(A)>0$
. Let
![]() $A\cap\mathscr{F}=\{B\cap A;\,B\in \mathscr{F}\}$
, which is a
$A\cap\mathscr{F}=\{B\cap A;\,B\in \mathscr{F}\}$
, which is a
![]() $\sigma$
-algebra on A, and let
$\sigma$
-algebra on A, and let
![]() $\mathbb{P}_A$
be a probability measure on
$\mathbb{P}_A$
be a probability measure on
![]() $(A, A\cap\mathscr{F})$
such that
$(A, A\cap\mathscr{F})$
such that
![]() $\mathbb{P}_A\!\left(B\cap A\right)=\mathbb{P}\!\left(B\middle|A\right)$
for all
$\mathbb{P}_A\!\left(B\cap A\right)=\mathbb{P}\!\left(B\middle|A\right)$
for all
![]() $B\in \mathscr{F}$
. Then we have the corresponding conditional expectation
$B\in \mathscr{F}$
. Then we have the corresponding conditional expectation
which equals 0 on
![]() $\textbf{1}_{A^c}$
. The proof relies on the following observations.
$\textbf{1}_{A^c}$
. The proof relies on the following observations.
Lemma 5.4.
For any random variable Y with
![]() $\mathbb{E}\vert Y\vert < \infty$
and
$\mathbb{E}\vert Y\vert < \infty$
and
![]() $A\in \mathscr{G}$
such that
$A\in \mathscr{G}$
such that
![]() $\mathbb{P}(A)>0$
,
$\mathbb{P}(A)>0$
,
Proof. Both sides are
![]() $\mathscr{F}$
-measurable, and for any
$\mathscr{F}$
-measurable, and for any
![]() $B\in \mathscr{F}$
,
$B\in \mathscr{F}$
,
 \begin{align} \mathbb{E}\!\left(\mathbb{E}\!\left(\mathbb{E}_A\!\left(Y\middle|A\cap\mathscr{F}\,\right)\middle|\mathscr{F}\,\right)\textbf{1}_B\right)&=\mathbb{E}\!\left(\mathbb{E}_A\!\left(Y\middle|A\cap\mathscr{F}\,\right)\textbf{1}_B\right)\nonumber \\&=\mathbb{E}\!\left(\mathbb{E}_A\!\left(Y\middle|A\cap\mathscr{F}\,\right)\textbf{1}_{B\cap A}\right)\nonumber \\&=\mathbb{E}\!\left(\mathbb{E}_A\!\left(\textbf{1}_{B\cap A}Y\middle|A\cap\mathscr{F}\,\right)\right)\nonumber \\&=\mathbb{P}(A)\mathbb{E}_A\!\left(\mathbb{E}_A\!\left(\textbf{1}_{B\cap A}Y\middle|A\cap\mathscr{F}\,\right)\right)\nonumber \\&=\mathbb{P}(A)\mathbb{E}_A\!\left(\textbf{1}_{B\cap A}Y\right)=\mathbb{E}\!\left(\textbf{1}_{B\cap A}Y\right)=\mathbb{E}\!\left(\mathbb{E}\!\left(\textbf{1}_A Y\middle|\mathscr{F}\,\right)\textbf{1}_B\right),\nonumber\end{align}
\begin{align} \mathbb{E}\!\left(\mathbb{E}\!\left(\mathbb{E}_A\!\left(Y\middle|A\cap\mathscr{F}\,\right)\middle|\mathscr{F}\,\right)\textbf{1}_B\right)&=\mathbb{E}\!\left(\mathbb{E}_A\!\left(Y\middle|A\cap\mathscr{F}\,\right)\textbf{1}_B\right)\nonumber \\&=\mathbb{E}\!\left(\mathbb{E}_A\!\left(Y\middle|A\cap\mathscr{F}\,\right)\textbf{1}_{B\cap A}\right)\nonumber \\&=\mathbb{E}\!\left(\mathbb{E}_A\!\left(\textbf{1}_{B\cap A}Y\middle|A\cap\mathscr{F}\,\right)\right)\nonumber \\&=\mathbb{P}(A)\mathbb{E}_A\!\left(\mathbb{E}_A\!\left(\textbf{1}_{B\cap A}Y\middle|A\cap\mathscr{F}\,\right)\right)\nonumber \\&=\mathbb{P}(A)\mathbb{E}_A\!\left(\textbf{1}_{B\cap A}Y\right)=\mathbb{E}\!\left(\textbf{1}_{B\cap A}Y\right)=\mathbb{E}\!\left(\mathbb{E}\!\left(\textbf{1}_A Y\middle|\mathscr{F}\,\right)\textbf{1}_B\right),\nonumber\end{align}
as claimed.
Lemma 5.5.
For any random variable Y with
![]() $\mathbb{E}\vert Y\vert <\infty$
and
$\mathbb{E}\vert Y\vert <\infty$
and
![]() $A\in \mathscr{G}$
such that
$A\in \mathscr{G}$
such that
![]() $\mathbb{P}(A)>0$
,
$\mathbb{P}(A)>0$
,
Proof. Both sides equal 0 on
![]() $A^c$
and are measurable on
$A^c$
and are measurable on
![]() $A\cap\mathscr{F}$
when restricted to A. From the construction of
$A\cap\mathscr{F}$
when restricted to A. From the construction of
![]() $ A\cap\mathscr{F}$
, any set
$ A\cap\mathscr{F}$
, any set
![]() $B^{\prime}\in A\cap\mathscr{F}$
is of the form
$B^{\prime}\in A\cap\mathscr{F}$
is of the form
![]() $B\cap A$
for some
$B\cap A$
for some
![]() $B\in\mathscr{F}$
. Hence (5.8) is equivalent to
$B\in\mathscr{F}$
. Hence (5.8) is equivalent to
for all
![]() $B\in \mathscr{F}$
. Now we have
$B\in \mathscr{F}$
. Now we have
 \begin{align} \mathbb{E}_A\!\left(\frac{\mathbb{E}\!\left(\textbf{1}_A Y \middle|\mathscr{F}\,\right)}{\mathbb{E}\!\left(\textbf{1}_A\middle|\mathscr{F}\,\right)}\textbf{1}_{A\cap B}\right)&=\frac{1}{\mathbb{P}(A)}\mathbb{E}\!\left(\frac{\mathbb{E}\!\left(\textbf{1}_A Y \middle|\mathscr{F}\,\right)}{\mathbb{E}\!\left(\textbf{1}_A\middle|\mathscr{F}\,\right)}\textbf{1}_A\textbf{1}_B\right)\nonumber \\&=\frac{1}{\mathbb{P}(A)}\mathbb{E}\!\left(\mathbb{E}\!\left(\frac{\mathbb{E}\!\left(\textbf{1}_A Y \middle|\mathscr{F}\,\right)}{\mathbb{E}\!\left(\textbf{1}_A\middle|\mathscr{F}\,\right)}\textbf{1}_A\textbf{1}_B\middle|\mathscr{F}\,\right)\right)\nonumber \\&=\frac{1}{\mathbb{P}(A)}\mathbb{E}\!\left(\mathbb{E}\!\left(\textbf{1}_A Y \middle|\mathscr{F}\,\right)\textbf{1}_B\right)=\frac{1}{\mathbb{P}(A)}\mathbb{E}\!\left(\mathbb{E}\!\left(\textbf{1}_A\textbf{1}_B Y \middle|\mathscr{F}\,\right)\right)\nonumber \\&=\frac{1}{\mathbb{P}(A)}\mathbb{E}\!\left(\textbf{1}_A\textbf{1}_B Y\right)=\mathbb{E}_A(\mathbb{E}_A(Y\textbf{1}_A\textbf{1}_B|\mathscr{F}))=\mathbb{E}_A(\mathbb{E}_A(Y|\mathscr{F})\textbf{1}_{A\cap B}),\nonumber\end{align}
\begin{align} \mathbb{E}_A\!\left(\frac{\mathbb{E}\!\left(\textbf{1}_A Y \middle|\mathscr{F}\,\right)}{\mathbb{E}\!\left(\textbf{1}_A\middle|\mathscr{F}\,\right)}\textbf{1}_{A\cap B}\right)&=\frac{1}{\mathbb{P}(A)}\mathbb{E}\!\left(\frac{\mathbb{E}\!\left(\textbf{1}_A Y \middle|\mathscr{F}\,\right)}{\mathbb{E}\!\left(\textbf{1}_A\middle|\mathscr{F}\,\right)}\textbf{1}_A\textbf{1}_B\right)\nonumber \\&=\frac{1}{\mathbb{P}(A)}\mathbb{E}\!\left(\mathbb{E}\!\left(\frac{\mathbb{E}\!\left(\textbf{1}_A Y \middle|\mathscr{F}\,\right)}{\mathbb{E}\!\left(\textbf{1}_A\middle|\mathscr{F}\,\right)}\textbf{1}_A\textbf{1}_B\middle|\mathscr{F}\,\right)\right)\nonumber \\&=\frac{1}{\mathbb{P}(A)}\mathbb{E}\!\left(\mathbb{E}\!\left(\textbf{1}_A Y \middle|\mathscr{F}\,\right)\textbf{1}_B\right)=\frac{1}{\mathbb{P}(A)}\mathbb{E}\!\left(\mathbb{E}\!\left(\textbf{1}_A\textbf{1}_B Y \middle|\mathscr{F}\,\right)\right)\nonumber \\&=\frac{1}{\mathbb{P}(A)}\mathbb{E}\!\left(\textbf{1}_A\textbf{1}_B Y\right)=\mathbb{E}_A(\mathbb{E}_A(Y\textbf{1}_A\textbf{1}_B|\mathscr{F}))=\mathbb{E}_A(\mathbb{E}_A(Y|\mathscr{F})\textbf{1}_{A\cap B}),\nonumber\end{align}
completing the proof.
Proof of Lemma 5.3 (continued). We start from the left-hand side of (5.7):
 \begin{align} & \quad {\textrm{Var}}\!\left(X\middle|\mathscr{F}\,\right)\nonumber \\&= \mathbb{E}\!\left(X^2\middle|\mathscr{F}\,\right)-\mathbb{E}\!\left(X\middle|\mathscr{F}\,\right)^2\nonumber \\&= \mathbb{E}\!\left(X^2\middle|\mathscr{F}\,\right)-\left(\mathbb{E}\!\left(X\textbf{1}_A\middle|\mathscr{F}\,\right)+\mathbb{E}\!\left(X\textbf{1}_{A^c}\middle|\mathscr{F}\,\right)\right)^2\nonumber \\&= \mathbb{E}\!\left(X^2\middle|\mathscr{F}\,\right)-\mathbb{E}\!\left(\mathbb{E}_A\!\left(X\textbf{1}_A\middle|A\cap\mathscr{F}\,\right)+\mathbb{E}_{A^c}\left(X\middle|A^c\cap\mathscr{F}\,\right)\middle|\mathscr{F}\,\right)^2\nonumber \\&\ge \mathbb{E}\!\left(X^2\middle|\mathscr{F}\,\right)-\mathbb{E}\!\left(\left(\mathbb{E}_A\!\left(X\textbf{1}_A\middle|A\cap\mathscr{F}\,\right)+\mathbb{E}_{A^c}\left(X\middle|A^c\cap\mathscr{F}\,\right)\right)^2\middle|\mathscr{F}\,\right)\nonumber \\&= \mathbb{E}\!\left(X^2\left(\textbf{1}_A+\textbf{1}_{A^c}\right)\middle|\mathscr{F}\,\right)-\mathbb{E}\!\left(\mathbb{E}_A\!\left(X\textbf{1}_A\middle|A\cap\mathscr{F}\,\right)^2+\mathbb{E}_{A^c}\!\left(X\middle|A^c\cap\mathscr{F}\,\right)^2\middle|\mathscr{F}\,\right)\nonumber \\&= \mathbb{E}\!\left(\mathbb{E}_A\!\left(X^2\middle| A\cap\mathscr{F}\,\right)+\mathbb{E}_{A^c}\!\left(X^2\middle| A^c\cap\mathscr{F}\,\right)\middle|\mathscr{F}\,\right)\nonumber\\ &\quad -\mathbb{E}\!\left(\mathbb{E}_A\!\left(X\textbf{1}_A\middle|A\cap\mathscr{F}\,\right)^2+\mathbb{E}_{A^c}\!\left(X\middle|A^c\cap\mathscr{F}\,\right)^2\middle|\mathscr{F}\,\right)\nonumber \\& = \mathbb{E}\!\left({\textrm{Var}}_A\left(X\middle| A\cap\mathscr{F}\,\right)+{\textrm{Var}}_{A^c}\left(X\middle| A^c\cap\mathscr{F}\,\right)\middle|\mathscr{F}\,\right),\end{align}
\begin{align} & \quad {\textrm{Var}}\!\left(X\middle|\mathscr{F}\,\right)\nonumber \\&= \mathbb{E}\!\left(X^2\middle|\mathscr{F}\,\right)-\mathbb{E}\!\left(X\middle|\mathscr{F}\,\right)^2\nonumber \\&= \mathbb{E}\!\left(X^2\middle|\mathscr{F}\,\right)-\left(\mathbb{E}\!\left(X\textbf{1}_A\middle|\mathscr{F}\,\right)+\mathbb{E}\!\left(X\textbf{1}_{A^c}\middle|\mathscr{F}\,\right)\right)^2\nonumber \\&= \mathbb{E}\!\left(X^2\middle|\mathscr{F}\,\right)-\mathbb{E}\!\left(\mathbb{E}_A\!\left(X\textbf{1}_A\middle|A\cap\mathscr{F}\,\right)+\mathbb{E}_{A^c}\left(X\middle|A^c\cap\mathscr{F}\,\right)\middle|\mathscr{F}\,\right)^2\nonumber \\&\ge \mathbb{E}\!\left(X^2\middle|\mathscr{F}\,\right)-\mathbb{E}\!\left(\left(\mathbb{E}_A\!\left(X\textbf{1}_A\middle|A\cap\mathscr{F}\,\right)+\mathbb{E}_{A^c}\left(X\middle|A^c\cap\mathscr{F}\,\right)\right)^2\middle|\mathscr{F}\,\right)\nonumber \\&= \mathbb{E}\!\left(X^2\left(\textbf{1}_A+\textbf{1}_{A^c}\right)\middle|\mathscr{F}\,\right)-\mathbb{E}\!\left(\mathbb{E}_A\!\left(X\textbf{1}_A\middle|A\cap\mathscr{F}\,\right)^2+\mathbb{E}_{A^c}\!\left(X\middle|A^c\cap\mathscr{F}\,\right)^2\middle|\mathscr{F}\,\right)\nonumber \\&= \mathbb{E}\!\left(\mathbb{E}_A\!\left(X^2\middle| A\cap\mathscr{F}\,\right)+\mathbb{E}_{A^c}\!\left(X^2\middle| A^c\cap\mathscr{F}\,\right)\middle|\mathscr{F}\,\right)\nonumber\\ &\quad -\mathbb{E}\!\left(\mathbb{E}_A\!\left(X\textbf{1}_A\middle|A\cap\mathscr{F}\,\right)^2+\mathbb{E}_{A^c}\!\left(X\middle|A^c\cap\mathscr{F}\,\right)^2\middle|\mathscr{F}\,\right)\nonumber \\& = \mathbb{E}\!\left({\textrm{Var}}_A\left(X\middle| A\cap\mathscr{F}\,\right)+{\textrm{Var}}_{A^c}\left(X\middle| A^c\cap\mathscr{F}\,\right)\middle|\mathscr{F}\,\right),\end{align}
where the inequality follows from Jensen’s inequality, and the third equality and the second-to-last equality are from Lemma 5.4. On the other hand, the right-hand side of (5.7) can be written as
 \begin{align} &\quad \mathbb{E}\!\left(X^2\textbf{1}_A+\left(\frac{\mathbb{E}\!\left(X\textbf{1}_A\middle|\mathscr{F}\,\right)}{\mathbb{P}\!\left(A\middle|\mathscr{F}\,\right)}\right)^2\textbf{1}_{A^c}\middle|\mathscr{F}\,\right)-\left(\mathbb{E}\!\left(X\textbf{1}_A\middle|\mathscr{F}\,\right)+\mathbb{E}\!\left(\frac{\mathbb{E}\!\left(X\textbf{1}_A\middle|\mathscr{F}\,\right)}{\mathbb{P}\!\left(A\middle|\mathscr{F}\,\right)}\textbf{1}_{A^c}\middle|\mathscr{F}\,\right)\right)^2\nonumber \\&=\mathbb{E}\!\left(X^2\textbf{1}_A\middle|\mathscr{F}\,\right)+\left(\frac{\mathbb{E}\!\left(X\textbf{1}_A\middle|\mathscr{F}\,\right)}{\mathbb{P}\!\left(A\middle|\mathscr{F}\,\right)}\right)^2\mathbb{P}\!\left(A^c\middle|\mathscr{F}\,\right)-\mathbb{E}\!\left(X\textbf{1}_A\middle|\mathscr{F}\,\right)^2\frac{1}{\mathbb{P}\!\left(A\middle|\mathscr{F}\,\right)^2}\nonumber \\&=\mathbb{E}\!\left(X^2\textbf{1}_A\middle|\mathscr{F}\,\right)-\left(\frac{\mathbb{E}\!\left(X\textbf{1}_A\middle|\mathscr{F}\,\right)}{\mathbb{P}\!\left(A\middle|\mathscr{F}\,\right)}\right)^2\mathbb{P}\!\left(A\middle|\mathscr{F}\,\right)\nonumber \\&=\mathbb{E}\!\left(\mathbb{E}_A\!\left(X^2\middle|A\cap \mathscr{F}\,\right)-\left(\frac{\mathbb{E}\!\left(X\textbf{1}_A\middle|\mathscr{F}\,\right)}{\mathbb{P}\!\left(A\middle|\mathscr{F}\,\right)}\right)^2\textbf{1}_A\middle|\mathscr{F}\,\right)\nonumber \\&=\mathbb{E}\!\left(\mathbb{E}_A\!\left(X^2\middle|A\cap \mathscr{F}\,\right)-\mathbb{E}_A\!\left(X\middle|A\cap \mathscr{F}\,\right)^2\middle|\mathscr{F}\,\right)\nonumber \\&=\mathbb{E}\!\left({\textrm{Var}}_A\left(X\middle| A\cap\mathscr{F}\,\right)\middle|\mathscr{F}\,\right),\end{align}
\begin{align} &\quad \mathbb{E}\!\left(X^2\textbf{1}_A+\left(\frac{\mathbb{E}\!\left(X\textbf{1}_A\middle|\mathscr{F}\,\right)}{\mathbb{P}\!\left(A\middle|\mathscr{F}\,\right)}\right)^2\textbf{1}_{A^c}\middle|\mathscr{F}\,\right)-\left(\mathbb{E}\!\left(X\textbf{1}_A\middle|\mathscr{F}\,\right)+\mathbb{E}\!\left(\frac{\mathbb{E}\!\left(X\textbf{1}_A\middle|\mathscr{F}\,\right)}{\mathbb{P}\!\left(A\middle|\mathscr{F}\,\right)}\textbf{1}_{A^c}\middle|\mathscr{F}\,\right)\right)^2\nonumber \\&=\mathbb{E}\!\left(X^2\textbf{1}_A\middle|\mathscr{F}\,\right)+\left(\frac{\mathbb{E}\!\left(X\textbf{1}_A\middle|\mathscr{F}\,\right)}{\mathbb{P}\!\left(A\middle|\mathscr{F}\,\right)}\right)^2\mathbb{P}\!\left(A^c\middle|\mathscr{F}\,\right)-\mathbb{E}\!\left(X\textbf{1}_A\middle|\mathscr{F}\,\right)^2\frac{1}{\mathbb{P}\!\left(A\middle|\mathscr{F}\,\right)^2}\nonumber \\&=\mathbb{E}\!\left(X^2\textbf{1}_A\middle|\mathscr{F}\,\right)-\left(\frac{\mathbb{E}\!\left(X\textbf{1}_A\middle|\mathscr{F}\,\right)}{\mathbb{P}\!\left(A\middle|\mathscr{F}\,\right)}\right)^2\mathbb{P}\!\left(A\middle|\mathscr{F}\,\right)\nonumber \\&=\mathbb{E}\!\left(\mathbb{E}_A\!\left(X^2\middle|A\cap \mathscr{F}\,\right)-\left(\frac{\mathbb{E}\!\left(X\textbf{1}_A\middle|\mathscr{F}\,\right)}{\mathbb{P}\!\left(A\middle|\mathscr{F}\,\right)}\right)^2\textbf{1}_A\middle|\mathscr{F}\,\right)\nonumber \\&=\mathbb{E}\!\left(\mathbb{E}_A\!\left(X^2\middle|A\cap \mathscr{F}\,\right)-\mathbb{E}_A\!\left(X\middle|A\cap \mathscr{F}\,\right)^2\middle|\mathscr{F}\,\right)\nonumber \\&=\mathbb{E}\!\left({\textrm{Var}}_A\left(X\middle| A\cap\mathscr{F}\,\right)\middle|\mathscr{F}\,\right),\end{align}
where the third equality follows from Lemma 5.4, and the second-to-last equality is from Lemma 5.5. Combining (5.9), (5.10), and Lemma 5.2 completes the proof.
Before going to the proof of Lemma 4.4, we need a lemma to show that under the stabilisation conditions, the cost of throwing away the terms with a large radius of stabilisation is negligible.
Lemma 5.6.
-
(a) (Unrestricted case.) If the score function is exponentially stabilising as in Definition 2.1, then we have
for some positive constants \begin{equation*}d_{TV}\big(W_\alpha, W_{\alpha,r}\big)\le C_1\alpha e^{-C_2r}\end{equation*}
\begin{equation*}d_{TV}\big(W_\alpha, W_{\alpha,r}\big)\le C_1\alpha e^{-C_2r}\end{equation*}
 $C_1$
,
$C_1$
,
 $C_2$
. If the score function is polynomially stabilising with parameter
$C_2$
. If the score function is polynomially stabilising with parameter
 $\beta$
in Definition 2.1, then we have for some positive constant C.
$\beta$
in Definition 2.1, then we have for some positive constant C. \begin{equation*}d_{TV}\big(W_\alpha, W_{\alpha,r}\big)\le C\alpha r^{-\beta}\end{equation*}
\begin{equation*}d_{TV}\big(W_\alpha, W_{\alpha,r}\big)\le C\alpha r^{-\beta}\end{equation*}
-
(b) (Restricted case.) If the score function is exponentially stabilising as in Definition 2.2, then we have
for some positive constants \begin{equation*}d_{TV}\big(\bar{W}_\alpha, \bar{W}_{\alpha,r}\big)\le C_1\alpha e^{-C_2r}\end{equation*}
\begin{equation*}d_{TV}\big(\bar{W}_\alpha, \bar{W}_{\alpha,r}\big)\le C_1\alpha e^{-C_2r}\end{equation*}
 $C_1$
,
$C_1$
,
 $C_2$
. If the score function is polynomially stabilising with parameter
$C_2$
. If the score function is polynomially stabilising with parameter
 $\beta$
in Definition 2.2, then we have for some positive constant C.
$\beta$
in Definition 2.2, then we have for some positive constant C. \begin{equation*}d_{TV}\big(\bar{W}_\alpha, \bar{W}_{\alpha,r}\big)\le C\alpha r^{-\beta}\end{equation*}
\begin{equation*}d_{TV}\big(\bar{W}_\alpha, \bar{W}_{\alpha,r}\big)\le C\alpha r^{-\beta}\end{equation*}
Proof. We first show that the statement is true for
![]() $\bar{W}_\alpha$
and
$\bar{W}_\alpha$
and
![]() $\bar{W}_{\alpha,r}$
. Recall that we defined
$\bar{W}_{\alpha,r}$
. Recall that we defined
![]() $M_1\sim \mathscr{L}_{T}$
as a random element independent of
$M_1\sim \mathscr{L}_{T}$
as a random element independent of
![]() $\Xi$
. From the construction of
$\Xi$
. From the construction of
![]() $\bar{W}_\alpha$
and
$\bar{W}_\alpha$
and
![]() $\bar{W}_{\alpha,r}$
, we can see that the event
$\bar{W}_{\alpha,r}$
, we can see that the event
![]() $\{\bar{W}_\alpha\neq \bar{W}_{\alpha,r}\}\subset\{\mbox{at least one }x\in \bar{\Xi}\cap\Gamma_\alpha\mbox{with }\bar{R}(x, \alpha)>r\}$
. From (5.4), we have
$\{\bar{W}_\alpha\neq \bar{W}_{\alpha,r}\}\subset\{\mbox{at least one }x\in \bar{\Xi}\cap\Gamma_\alpha\mbox{with }\bar{R}(x, \alpha)>r\}$
. From (5.4), we have
 \begin{align*} d_{TV}\big(\bar{W}_\alpha, \bar{W}_{\alpha,r}\big)&\le \mathbb{P}\!\left(\big\{\bar{W}_\alpha\neq \bar{W}_{\alpha,r}\big\}\right) \\&\le \mathbb{P}\!\left(\big\{\mbox{at least one }x\in \bar{\Xi}\cap\Gamma_\alpha\ {\mbox{such that }}\bar{R}(x, \alpha)>r\big\}\right) \\ &\le \mathbb{E}\int_{\Gamma_\alpha}\textbf{1}_{\bar{R}(x,\alpha)>r} \bar{\Xi}(dx) \\ &=\int_{\Gamma_\alpha}\mathbb{E}\!\left(\textbf{1}_{\bar{R}\big(x,{M_1},\alpha, \Xi+\delta_{(x, {M_1})}\big)>r}\right)\lambda dx \\ &=\int_{\Gamma_\alpha}\mathbb{P}\!\left(\bar{R}\big(x,{M_1},\alpha, \Xi+\delta_{(x, {M_1})}\big)>r\right) \lambda dx \\ &\le \alpha\lambda\bar{\tau}(r),\end{align*}
\begin{align*} d_{TV}\big(\bar{W}_\alpha, \bar{W}_{\alpha,r}\big)&\le \mathbb{P}\!\left(\big\{\bar{W}_\alpha\neq \bar{W}_{\alpha,r}\big\}\right) \\&\le \mathbb{P}\!\left(\big\{\mbox{at least one }x\in \bar{\Xi}\cap\Gamma_\alpha\ {\mbox{such that }}\bar{R}(x, \alpha)>r\big\}\right) \\ &\le \mathbb{E}\int_{\Gamma_\alpha}\textbf{1}_{\bar{R}(x,\alpha)>r} \bar{\Xi}(dx) \\ &=\int_{\Gamma_\alpha}\mathbb{E}\!\left(\textbf{1}_{\bar{R}\big(x,{M_1},\alpha, \Xi+\delta_{(x, {M_1})}\big)>r}\right)\lambda dx \\ &=\int_{\Gamma_\alpha}\mathbb{P}\!\left(\bar{R}\big(x,{M_1},\alpha, \Xi+\delta_{(x, {M_1})}\big)>r\right) \lambda dx \\ &\le \alpha\lambda\bar{\tau}(r),\end{align*}
which, together with the stabilisation conditions, gives the claim for
![]() $\bar{W}_{\alpha}$
.
$\bar{W}_{\alpha}$
.
The statement is also true for
![]() $W_\alpha$
, which can be proved by replacing
$W_\alpha$
, which can be proved by replacing
![]() $\bar{W}_\alpha$
with the corresponding
$\bar{W}_\alpha$
with the corresponding
![]() $W_\alpha$
,
$W_\alpha$
,
![]() $\bar{W}_{\alpha,r}$
with
$\bar{W}_{\alpha,r}$
with
![]() $W_{\alpha,r}$
,
$W_{\alpha,r}$
,
![]() $\bar{R}(x,\alpha)$
with R(x),
$\bar{R}(x,\alpha)$
with R(x),
![]() $\bar{R}(x,{M_1},\alpha,\Xi+\delta_{(x, {M_1})})$
with
$\bar{R}(x,{M_1},\alpha,\Xi+\delta_{(x, {M_1})})$
with
![]() $R(x,{M_1},\Xi+\delta_{(x, {M_1})})$
, and
$R(x,{M_1},\Xi+\delta_{(x, {M_1})})$
, and
![]() $\bar{\tau}$
with
$\bar{\tau}$
with
![]() $\tau.$
$\tau.$
Proof of Lemma
4.1. For convenience, we write
![]() $G_n$
,
$G_n$
,
![]() $g_n$
, and
$g_n$
, and
![]() $\psi_n$
for the distribution, density, and characteristic functions, respectively, of
$\psi_n$
for the distribution, density, and characteristic functions, respectively, of
![]() $T_n$
. It is well known that the triangular density
$T_n$
. It is well known that the triangular density
![]() $\kappa_a$
has the characteristic function
$\kappa_a$
has the characteristic function
which gives
Using the fact that the convolution of two symmetric unimodal distributions on
![]() $\mathbb{R}$
is unimodal [Reference Wintner50], we can conclude that the distribution of
$\mathbb{R}$
is unimodal [Reference Wintner50], we can conclude that the distribution of
![]() $T_n$
is unimodal and symmetric. This ensures that
$T_n$
is unimodal and symmetric. This ensures that
Applying the inversion formula, we have

where
![]() ${\mbox{i}}=\sqrt{-1}$
, and the second equality is due to the fact that
${\mbox{i}}=\sqrt{-1}$
, and the second equality is due to the fact that
![]() $\sin\!(sx)\psi_n(s)$
is an odd function. Obviously,
$\sin\!(sx)\psi_n(s)$
is an odd function. Obviously,
![]() $g_n(x)\le g_n(0)$
, so we need to establish an upper bound for
$g_n(x)\le g_n(0)$
, so we need to establish an upper bound for
![]() $g_n(0)$
. A direct verification gives
$g_n(0)$
. A direct verification gives
which implies
 \begin{align} g_n(0)&\le \frac1{a\pi} \left\{\int_0^{2\pi}e^{-\frac{ns^2}{12}}ds+\int_{2\pi}^\infty \left(\frac 4{s^2}\right)^nds\right\}\nonumber\\ &\le \frac1{a\pi\sqrt{n}}\int_0^\infty e^{-\frac{s^2}{12}}ds+\frac{2}{a(2n-1)\pi^{2n}}\nonumber\\ & = \frac1a\sqrt{\frac{3}{\pi n}}+\frac{2}{a(2n-1)\pi^{2n}}.\end{align}
\begin{align} g_n(0)&\le \frac1{a\pi} \left\{\int_0^{2\pi}e^{-\frac{ns^2}{12}}ds+\int_{2\pi}^\infty \left(\frac 4{s^2}\right)^nds\right\}\nonumber\\ &\le \frac1{a\pi\sqrt{n}}\int_0^\infty e^{-\frac{s^2}{12}}ds+\frac{2}{a(2n-1)\pi^{2n}}\nonumber\\ & = \frac1a\sqrt{\frac{3}{\pi n}}+\frac{2}{a(2n-1)\pi^{2n}}.\end{align}
Proof of Lemma
4.2. We construct a maximal coupling [Reference Barbour, Holst and Janson5, p. 254] (X, Y) such that
![]() $X\sim F$
,
$X\sim F$
,
![]() $Y\sim G$
, and
$Y\sim G$
, and
![]() $d_{TV}(F,G)=\mathbb{P}(X\ne Y)$
. The Lebesgue decomposition (1.1) ensures that there exists an
$d_{TV}(F,G)=\mathbb{P}(X\ne Y)$
. The Lebesgue decomposition (1.1) ensures that there exists an
![]() $A\in \mathscr{B}\!\left(\mathbb{R}\right)$
such that
$A\in \mathscr{B}\!\left(\mathbb{R}\right)$
such that
![]() $F_a(A)=1$
and
$F_a(A)=1$
and
![]() $F_s(A)=0$
. Define
$F_s(A)=0$
. Define
![]() $\mu_G(B)=\mathbb{P}\!\left(X\in B\cap A,X= Y\right)\le \alpha_FF_a(B)$
for
$\mu_G(B)=\mathbb{P}\!\left(X\in B\cap A,X= Y\right)\le \alpha_FF_a(B)$
for
![]() $B\in \mathscr{B}\!\left(\mathbb{R}\right)$
, so
$B\in \mathscr{B}\!\left(\mathbb{R}\right)$
, so
![]() $\mu_G$
is absolutely continuous with respect to the Lebesgue measure. On the other hand,
$\mu_G$
is absolutely continuous with respect to the Lebesgue measure. On the other hand,
hence
![]() $\alpha_G\ge \mu_G(\mathbb{R})= \alpha_F-\mathbb{P}\!\left(X\neq Y\right)=\alpha_F-d_{TV}\!\left(F, G\right)>0$
.
$\alpha_G\ge \mu_G(\mathbb{R})= \alpha_F-\mathbb{P}\!\left(X\neq Y\right)=\alpha_F-d_{TV}\!\left(F, G\right)>0$
.
Proof of Lemma
4.3. Since
![]() $F_i$
is non-singular, there exists a non-zero sub-probability measure
$F_i$
is non-singular, there exists a non-zero sub-probability measure
![]() $\mu_{i}$
with a density
$\mu_{i}$
with a density
![]() $f_{i}$
such that
$f_{i}$
such that
![]() $\mu_i(dx)=f_i(x)dx\le dF_i(x)$
for
$\mu_i(dx)=f_i(x)dx\le dF_i(x)$
for
![]() $x\in\mathbb{R}$
. Without loss of generality, we can assume that both
$x\in\mathbb{R}$
. Without loss of generality, we can assume that both
![]() $f_{1}$
and
$f_{1}$
and
![]() $f_{2}$
are bounded with bounded support, which ensures that
$f_{2}$
are bounded with bounded support, which ensures that
![]() $f_{1}\ast f_{2}$
is continuous (for the case of
$f_{1}\ast f_{2}$
is continuous (for the case of
![]() $f_{1}= f_{2}$
, see [Reference Lindvall33, p. 79]). In fact, as
$f_{1}= f_{2}$
, see [Reference Lindvall33, p. 79]). In fact, as
![]() $f_{1}$
is a density, one can find a sequence of continuous functions
$f_{1}$
is a density, one can find a sequence of continuous functions
![]() $\{f_{1n}\,:\, n\ge 1\}$
satisfying
$\{f_{1n}\,:\, n\ge 1\}$
satisfying
![]() $|f_{1n}-f_{1}|_1\rightarrow0$
as
$|f_{1n}-f_{1}|_1\rightarrow0$
as
![]() $n\to \infty$
, where
$n\to \infty$
, where
![]() $|\cdot|_1$
is the
$|\cdot|_1$
is the
![]() $L_1$
norm. Now, with
$L_1$
norm. Now, with
![]() $|\cdot|_\infty$
denoting the supremum norm,
$|\cdot|_\infty$
denoting the supremum norm,
![]() $|f_{1n}* f_{2}-f_{1}* f_{2}|_\infty\le |f_{2}|_\infty|f_{1n}-f_{1}|_1\to 0$
as
$|f_{1n}* f_{2}-f_{1}* f_{2}|_\infty\le |f_{2}|_\infty|f_{1n}-f_{1}|_1\to 0$
as
![]() $n\to\infty$
. However, since the continuity is preserved under the supremum norm, the continuity of
$n\to\infty$
. However, since the continuity is preserved under the supremum norm, the continuity of
![]() $f_{1}\ast f_{2}$
follows.
$f_{1}\ast f_{2}$
follows.
Referring to Figure 9, since
![]() $f_{1}\ast f_{2}\not\equiv0$
, we can find
$f_{1}\ast f_{2}\not\equiv0$
, we can find
![]() $u\in\mathbb{R}$
and
$u\in\mathbb{R}$
and
![]() $v>0$
such that
$v>0$
such that
![]() $f_{1}\ast f_{2}(u)>0$
and
$f_{1}\ast f_{2}(u)>0$
and
Let
![]() $\theta=vb$
and
$\theta=vb$
and
![]() $a=v$
; then
$a=v$
; then
![]() $H=\frac1{1-\theta}(F_1\ast F_2-\theta K_a\ast\delta_u)$
is a distribution function, and the claim follows.
$H=\frac1{1-\theta}(F_1\ast F_2-\theta K_a\ast\delta_u)$
is a distribution function, and the claim follows.

Figure 9. Existence of u and v.
Proof of Lemma
4.4. The idea of the proof is to use the radius of stabilisation to limit the effect of dependence, pass the non-singularity property to the truncated score function
![]() $\eta(\left(x,m\right)\!, \Xi)\textbf{1}_{R(x)\le r}$
$\eta(\left(x,m\right)\!, \Xi)\textbf{1}_{R(x)\le r}$
![]() $\left(\mbox{resp.}\eta(\left(x,m\right)\!, \Xi,\Gamma_\alpha)\textbf{1}_{\bar{R}(x,\alpha)\le r}\right)$
, and dig out the maximum number of cubes in the carrier space
$\left(\mbox{resp.}\eta(\left(x,m\right)\!, \Xi,\Gamma_\alpha)\textbf{1}_{\bar{R}(x,\alpha)\le r}\right)$
, and dig out the maximum number of cubes in the carrier space
![]() $\Gamma_\alpha$
such that the truncated score functions on these cubes are independent. Then we can apply Lemmas 4.2 and 4.3 to find the component with the form of a convolution of triangular distributions, which, together with the property of the triangular distributions in Lemma 4.1, implies the conclusion. The order of the bound is then determined by the reciprocal of the number of the cubes, as in the Berry–Esseen bound. Except for notational complexity, the proof of the restricted case is the same, so we first focus on the unrestricted case.
$\Gamma_\alpha$
such that the truncated score functions on these cubes are independent. Then we can apply Lemmas 4.2 and 4.3 to find the component with the form of a convolution of triangular distributions, which, together with the property of the triangular distributions in Lemma 4.1, implies the conclusion. The order of the bound is then determined by the reciprocal of the number of the cubes, as in the Berry–Esseen bound. Except for notational complexity, the proof of the restricted case is the same, so we first focus on the unrestricted case.
From Assumption 2.2, for the restricted case, we can find
![]() $\bar{g}$
,
$\bar{g}$
,
![]() $\bar{\eta}$
, and R corresponding to
$\bar{\eta}$
, and R corresponding to
![]() $\eta$
such that the stabilisation radius R of
$\eta$
such that the stabilisation radius R of
![]() $\bar{\eta}$
satisfies the same stabilisation property as
$\bar{\eta}$
satisfies the same stabilisation property as
![]() $\eta$
in the sense of Definition 2.1. Because
$\eta$
in the sense of Definition 2.1. Because
![]() $N_0$
is a bounded set, there exists an
$N_0$
is a bounded set, there exists an
![]() $r_1\in \mathbb{R}_+$
such that
$r_1\in \mathbb{R}_+$
such that
![]() $N_0\subset B(0,r_1)$
. For convenience, we write the random variables
$N_0\subset B(0,r_1)$
. For convenience, we write the random variables
and write the event
![]() $\{Y\neq Y_r\}$
as
$\{Y\neq Y_r\}$
as
![]() $E_r$
for
$E_r$
for
![]() $r\in \mathbb{R}_+$
. We can see that
$r\in \mathbb{R}_+$
. We can see that
and the right-hand side is a decreasing function of r. Under any stabilisation condition in Lemma 4.4, we can show that
![]() $\mathbb{P}\!\left(E_r\right)\to0$
as
$\mathbb{P}\!\left(E_r\right)\to0$
as
![]() $r\to\infty$
, that is,
$r\to\infty$
, that is,
![]() $Y_r$
converges to Y a.s. In fact,
$Y_r$
converges to Y a.s. In fact,
 \begin{align} &\quad \mathbb{P}\big(E^{\prime}_r\big) \nonumber\\ &\le \mathbb{P}\!\left(\{\mbox{there is at least one point }x\in \bar{\Xi}\cap B(0,r_1+r)\mbox{ such that } r\le R(x)\}\right) \\& \quad +\mathbb{P}\!\left(\{\mbox{there is at least one point }x\in \bar{\Xi}\cap B(0,r_1+r)^c\mbox{ such that } |x|-r_1\le R(x)\}\right). \nonumber\end{align}
\begin{align} &\quad \mathbb{P}\big(E^{\prime}_r\big) \nonumber\\ &\le \mathbb{P}\!\left(\{\mbox{there is at least one point }x\in \bar{\Xi}\cap B(0,r_1+r)\mbox{ such that } r\le R(x)\}\right) \\& \quad +\mathbb{P}\!\left(\{\mbox{there is at least one point }x\in \bar{\Xi}\cap B(0,r_1+r)^c\mbox{ such that } |x|-r_1\le R(x)\}\right). \nonumber\end{align}
Using the property of the Palm process (5.4), we can see that the first term of (5.13) satisfies
 \begin{align} &\mathbb{P}\!\left(\{\mbox{there is at least one point }x\in \bar{\Xi}\cap B(0,r_1+r)\mbox{ such that } r\le R(x)\}\right)\nonumber \\\le\, & \mathbb{E}\int_{B(0,r_1+r)}\textbf{1}_{R(x)\ge r}\bar{\Xi}(dx) =\int_{B(0,r_1+r)}\mathbb{E}\textbf{1}_{R\Big(x, {M_1},\Xi+\delta_{\big(x,{M_1}\big)}\Big)\ge r}\lambda dx\nonumber \\= & \int_{B(0,r_1+r)}\mathbb{P}\!\left(R\Big(x, {M_1},\Xi+\delta_{\big(x,{M_1}\big)}\Big)\ge r\right)\lambda dx \nonumber \\ \le & \int_{B(0,r_1+r)}\tau(r)\lambda dx= \frac{\lambda(r_1+r)^d\pi^{d/2}\tau(r)}{\Gamma\big(\frac{d}{2}+1\big)},\end{align}
\begin{align} &\mathbb{P}\!\left(\{\mbox{there is at least one point }x\in \bar{\Xi}\cap B(0,r_1+r)\mbox{ such that } r\le R(x)\}\right)\nonumber \\\le\, & \mathbb{E}\int_{B(0,r_1+r)}\textbf{1}_{R(x)\ge r}\bar{\Xi}(dx) =\int_{B(0,r_1+r)}\mathbb{E}\textbf{1}_{R\Big(x, {M_1},\Xi+\delta_{\big(x,{M_1}\big)}\Big)\ge r}\lambda dx\nonumber \\= & \int_{B(0,r_1+r)}\mathbb{P}\!\left(R\Big(x, {M_1},\Xi+\delta_{\big(x,{M_1}\big)}\Big)\ge r\right)\lambda dx \nonumber \\ \le & \int_{B(0,r_1+r)}\tau(r)\lambda dx= \frac{\lambda(r_1+r)^d\pi^{d/2}\tau(r)}{\Gamma\big(\frac{d}{2}+1\big)},\end{align}
and the second term is bounded by
 \begin{align} &\mathbb{P}\!\left(\{\mbox{there is at least one point }x\in \bar{\Xi}\cap B(0,r_1+r)^c\mbox{ such that } |x|-r_1\le R(x)\}\right)\nonumber \\\le &\mathbb{E}\int_{B(0,r_1+r)^c}\textbf{1}_{R(x)\ge |x|-r_1}\bar{\Xi}(dx)\nonumber = \int_{B(0,r_1+r)^c}\mathbb{E}\textbf{1}_{R\Big(x, {M_1},\Xi+\delta_{\big(x,{M_1}\big)}\Big)\ge |x|-r_1}\lambda dx\\ = & \int_{B(0,r_1+r)^c}\mathbb{P}\!\left(R\Big(x, {M_1},\Xi+\delta_{\big(x,{M_1}\big)}\Big)\ge |x|-r_1\right)\lambda dx \nonumber\\ \le & \int_{B(0,r_1+r)^c}\tau(|x|-r_1)\lambda dx= \int_{r_1+r}^\infty\frac{d\lambda t^{d-1}\pi^{d/2}\tau(t-r_1)}{\Gamma\big(\frac{d}{2}+1\big)}dt.\end{align}
\begin{align} &\mathbb{P}\!\left(\{\mbox{there is at least one point }x\in \bar{\Xi}\cap B(0,r_1+r)^c\mbox{ such that } |x|-r_1\le R(x)\}\right)\nonumber \\\le &\mathbb{E}\int_{B(0,r_1+r)^c}\textbf{1}_{R(x)\ge |x|-r_1}\bar{\Xi}(dx)\nonumber = \int_{B(0,r_1+r)^c}\mathbb{E}\textbf{1}_{R\Big(x, {M_1},\Xi+\delta_{\big(x,{M_1}\big)}\Big)\ge |x|-r_1}\lambda dx\\ = & \int_{B(0,r_1+r)^c}\mathbb{P}\!\left(R\Big(x, {M_1},\Xi+\delta_{\big(x,{M_1}\big)}\Big)\ge |x|-r_1\right)\lambda dx \nonumber\\ \le & \int_{B(0,r_1+r)^c}\tau(|x|-r_1)\lambda dx= \int_{r_1+r}^\infty\frac{d\lambda t^{d-1}\pi^{d/2}\tau(t-r_1)}{\Gamma\big(\frac{d}{2}+1\big)}dt.\end{align}
When the score function satisfies one of the stabilisation conditions, both bounds in (5.14) and (5.15) converge to 0 as
![]() $r\rightarrow \infty$
, so
$r\rightarrow \infty$
, so
![]() $\mathbb{P}\big(E_r\big)\le \mathbb{P}\big(E^{\prime}_r\big)\rightarrow 0$
as
$\mathbb{P}\big(E_r\big)\le \mathbb{P}\big(E^{\prime}_r\big)\rightarrow 0$
as
![]() $r\rightarrow \infty$
.
$r\rightarrow \infty$
.
For two measures
![]() $\mu_1, \mu_2$
, we write
$\mu_1, \mu_2$
, we write
![]() $\mu_1\preceq\mu_2$
if
$\mu_1\preceq\mu_2$
if
![]() $\mu_1(A)\le\mu_2(A)$
for all measurable sets A. The non-singularity in Assumption 2.4 ensures that, with positive probability, the conditional distribution
$\mu_1(A)\le\mu_2(A)$
for all measurable sets A. The non-singularity in Assumption 2.4 ensures that, with positive probability, the conditional distribution
![]() $\mathscr{L}\!\left(Y\middle|\sigma\!\left(\Xi_{N_0^c}\right)\right)$
is non-singular. So we can find a
$\mathscr{L}\!\left(Y\middle|\sigma\!\left(\Xi_{N_0^c}\right)\right)$
is non-singular. So we can find a
![]() $\sigma\!\left(\Xi_{N_0^c}\right)$
-measurable random measure
$\sigma\!\left(\Xi_{N_0^c}\right)$
-measurable random measure
![]() $\xi$
on
$\xi$
on
![]() $\mathbb{R}$
such that
$\mathbb{R}$
such that
![]() $\xi\preceq \mathscr{L}\!\left(Y\middle|\sigma\!\left(\Xi_{N_0^c}\right)\right)$
a.s.,
$\xi\preceq \mathscr{L}\!\left(Y\middle|\sigma\!\left(\Xi_{N_0^c}\right)\right)$
a.s.,
![]() $\mathbb{P}\!\left(\xi\!\left(\mathbb{R}\right)>0\right)>0$
, and
$\mathbb{P}\!\left(\xi\!\left(\mathbb{R}\right)>0\right)>0$
, and
![]() $\xi$
is absolutely continuous [Reference Kallenberg26, Lemma 2.1]. Since
$\xi$
is absolutely continuous [Reference Kallenberg26, Lemma 2.1]. Since
we can find a
![]() $p>0$
such that
$p>0$
such that
![]() $\mathbb{P}\!\left(\xi(\mathbb{R})>p\right)>4p$
. Because
$\mathbb{P}\!\left(\xi(\mathbb{R})>p\right)>4p$
. Because
![]() $E^{\prime}_r$
is decreasing in the sense of inclusion in r, and
$E^{\prime}_r$
is decreasing in the sense of inclusion in r, and
![]() $\mathbb{P}\!\left(E^{\prime}_r\right)\rightarrow 0$
as
$\mathbb{P}\!\left(E^{\prime}_r\right)\rightarrow 0$
as
![]() $r\rightarrow \infty,$
we can find an
$r\rightarrow \infty,$
we can find an
![]() $R_0\in \mathbb{R}_+$
such that
$R_0\in \mathbb{R}_+$
such that
![]() $\mathbb{P}\big(E^{\prime}_{R_0}\big)\le p^2$
, which ensures
$\mathbb{P}\big(E^{\prime}_{R_0}\big)\le p^2$
, which ensures
If we write
![]() $\tilde{Y}\,:\!=\,Y\textbf{1}_{E^{{{\prime}_{R_0}}^{c}}}$
,
$\tilde{Y}\,:\!=\,Y\textbf{1}_{E^{{{\prime}_{R_0}}^{c}}}$
,
![]() $A_1\,:\!=\,\left\{d_{TV}\left(\left.Y,\tilde{Y}\right|\sigma\!\left(\Xi_{N_0^c}\right)\right)>p/2\right\}$
,
$A_1\,:\!=\,\left\{d_{TV}\left(\left.Y,\tilde{Y}\right|\sigma\!\left(\Xi_{N_0^c}\right)\right)>p/2\right\}$
,
![]() $A_2\,:\!=\,\{\xi(\mathbb{R})>p\}$
, then
$A_2\,:\!=\,\{\xi(\mathbb{R})>p\}$
, then
![]() $A_1$
and
$A_1$
and
![]() $A_2$
are both
$A_2$
are both
![]() $\sigma\!\left(\Xi_{N_0^c}\right)$
-measurable, and
$\sigma\!\left(\Xi_{N_0^c}\right)$
-measurable, and
giving
![]() $\mathbb{P}\big(A_2\cap A_1^c\big)>2p$
. For
$\mathbb{P}\big(A_2\cap A_1^c\big)>2p$
. For
![]() $\omega \in A_1^c\cap A_2$
,
$\omega \in A_1^c\cap A_2$
,
![]() $d_{TV}\!\left(\left.Y,\tilde{Y}\right|\sigma\!\left(\Xi_{N_0^c}\right)\right)(\omega)<p/2$
and
$d_{TV}\!\left(\left.Y,\tilde{Y}\right|\sigma\!\left(\Xi_{N_0^c}\right)\right)(\omega)<p/2$
and
![]() $\xi(\omega)(\mathbb{R})>p$
. By Lemma 4.2 and (5.16), there exists an absolutely continuous
$\xi(\omega)(\mathbb{R})>p$
. By Lemma 4.2 and (5.16), there exists an absolutely continuous
![]() $\sigma\!\left(\Xi_{N_0^c}\right)$
-measurable random measure
$\sigma\!\left(\Xi_{N_0^c}\right)$
-measurable random measure
![]() $\tilde{\xi}$
such that
$\tilde{\xi}$
such that
![]() $\tilde{\xi}\preceq \mathscr{L}\!\left(\tilde{Y}\middle|\sigma\!\left(\Xi_{N_0^c}\right)\right)$
a.s. and
$\tilde{\xi}\preceq \mathscr{L}\!\left(\tilde{Y}\middle|\sigma\!\left(\Xi_{N_0^c}\right)\right)$
a.s. and
![]() $\mathbb{P}\!\left(\tilde{\xi}\!\left(\mathbb{R}\right)>\frac{p}{2}\right)>2p$
. We write
$\mathbb{P}\!\left(\tilde{\xi}\!\left(\mathbb{R}\right)>\frac{p}{2}\right)>2p$
. We write
![]() $\Xi^{\prime}$
as an independent copy of
$\Xi^{\prime}$
as an independent copy of
![]() $\Xi$
, and the corresponding
$\Xi$
, and the corresponding
![]() $Y_r$
and
$Y_r$
and
![]() $\tilde{\xi}$
as
$\tilde{\xi}$
as
![]() $Y^{\prime}_r$
and
$Y^{\prime}_r$
and
![]() $\tilde{\xi}^{\prime}$
, respectively. Using Lemma 4.3, we can find
$\tilde{\xi}^{\prime}$
, respectively. Using Lemma 4.3, we can find
![]() $\sigma\!\left(\Xi_{N_0^c}, \Xi^{\prime}_{N_0^c}\right)$
-measurable random variables
$\sigma\!\left(\Xi_{N_0^c}, \Xi^{\prime}_{N_0^c}\right)$
-measurable random variables
![]() $\Theta_1\ge 0,\ \Theta_2\ge 0$
and
$\Theta_1\ge 0,\ \Theta_2\ge 0$
and
![]() $U\in \mathbb{R}$
such that
$U\in \mathbb{R}$
such that
![]() $\mathbb{P}(\Theta_1>0,\Theta_2>0)=4p^2$
, and
$\mathbb{P}(\Theta_1>0,\Theta_2>0)=4p^2$
, and
However,
and from Remark 4.1, we can find an
![]() ${\epsilon}>0$
such that
${\epsilon}>0$
such that
for a
![]() $\sigma\!\left(\Xi_{N_0^c}, \Xi^{\prime}_{N_0^c}\right)$
-measurable U. From the fact that we can write
$\sigma\!\left(\Xi_{N_0^c}, \Xi^{\prime}_{N_0^c}\right)$
-measurable U. From the fact that we can write
![]() $Y_r=\tilde Y+Y_r\textbf{1}_{E^{\prime}_{R_0}}$
, we have, for any
$Y_r=\tilde Y+Y_r\textbf{1}_{E^{\prime}_{R_0}}$
, we have, for any
![]() $B\in \mathscr{B}(\mathbb{R}\backslash\{0\})$
,
$B\in \mathscr{B}(\mathbb{R}\backslash\{0\})$
,
 \begin{align*} \mathbb{P}\!\left(\left.Y_r\in B\right|\sigma\!\left(\Xi_{N_0^c}\right)\right)& = \mathbb{P}\!\left(\left.\tilde Y\in B, {E^{\prime}_{R_0}}^c\right|\sigma\!\left(\Xi_{N_0^c}\right)\right)+\mathbb{P}\!\left(\left.Y_r\in B, E^{{\prime}_{R_0}}\right|\sigma\!\left(\Xi_{N_0^c}\right)\right)\\ &\ge \mathbb{P}\!\left(\left.\tilde Y\in B,{E^{{\prime}_{R_0}}}^c\right|\sigma\!\left(\Xi_{N_0^c}\right)\right)\\ & = \mathbb{P}\!\left(\left.\tilde Y\in B\right|\sigma\!\left(\Xi_{N_0^c}\right)\right).\end{align*}
\begin{align*} \mathbb{P}\!\left(\left.Y_r\in B\right|\sigma\!\left(\Xi_{N_0^c}\right)\right)& = \mathbb{P}\!\left(\left.\tilde Y\in B, {E^{\prime}_{R_0}}^c\right|\sigma\!\left(\Xi_{N_0^c}\right)\right)+\mathbb{P}\!\left(\left.Y_r\in B, E^{{\prime}_{R_0}}\right|\sigma\!\left(\Xi_{N_0^c}\right)\right)\\ &\ge \mathbb{P}\!\left(\left.\tilde Y\in B,{E^{{\prime}_{R_0}}}^c\right|\sigma\!\left(\Xi_{N_0^c}\right)\right)\\ & = \mathbb{P}\!\left(\left.\tilde Y\in B\right|\sigma\!\left(\Xi_{N_0^c}\right)\right).\end{align*}
Hence
 \begin{align} &\mathscr{L}\!\left(Y_r\middle|\sigma\!\left(\Xi_{N_0^c}\right)\right)({\cdot})\ge \mathscr{L}\!\left(\tilde Y\middle|\sigma\!\left(\Xi_{N_0^c}\right)\right)({\cdot}\backslash\{0\})\nonumber\\ &\ge \tilde\xi ({\cdot}\backslash\{0\})=\tilde\xi ({\cdot}) \mbox{ a.s. for all }r\ge R_0.\end{align}
\begin{align} &\mathscr{L}\!\left(Y_r\middle|\sigma\!\left(\Xi_{N_0^c}\right)\right)({\cdot})\ge \mathscr{L}\!\left(\tilde Y\middle|\sigma\!\left(\Xi_{N_0^c}\right)\right)({\cdot}\backslash\{0\})\nonumber\\ &\ge \tilde\xi ({\cdot}\backslash\{0\})=\tilde\xi ({\cdot}) \mbox{ a.s. for all }r\ge R_0.\end{align}
Therefore, using
![]() $U\in \mathscr{A}$
to stand for U being
$U\in \mathscr{A}$
to stand for U being
![]() $\mathscr{A}$
-measurable, we have
$\mathscr{A}$
-measurable, we have
 \begin{align*} &\sup_{U\in \sigma\!\left(\Xi_{B(N_0,2r)\backslash N_0},\Xi^{\prime}_{B(N_0,2r)\backslash N_0}\right)}\begin{aligned} \mathbb{P}&\left\{\mathscr{L}\!\left(Y_r\middle|\sigma\!\left(\Xi_{B(N_0,2r)\backslash N_0}\right)\right)\star\mathscr{L}\!\left(Y^{\prime}_r\middle|\sigma\!\left(\Xi^{\prime}_{B(N_0,2r)\backslash N_0}\right)\right)\right.\\ &\left.{\succeq} {\epsilon}^2K_{\epsilon}\star \delta_U\right\} \end{aligned} \\ &=\sup_{U\in \sigma\!\left(\Xi_{N_0^c},\Xi^{\prime}_{N_0^c}\right)} \mathbb{P}\!\left\{\mathscr{L}\!\left(Y_r\middle|\sigma\!\left(\Xi_{B(N_0,2r)\backslash N_0}\right)\right)\star\mathscr{L}\!\left(Y^{\prime}_r\middle|\sigma\!\left(\Xi^{\prime}_{B(N_0,2r)\backslash N_0}\right)\right){\succeq} {\epsilon}^2K_{\epsilon}\star \delta_U\right\} \\ &= \sup_{U\in \sigma\!\left(\Xi_{N_0^c},\Xi^{\prime}_{N_0^c}\right)}\mathbb{P}\!\left\{\mathscr{L}\!\left(Y_r\middle|\sigma\!\left(\Xi_{N_0^c}\right)\right)\star\mathscr{L}\!\left(Y^{\prime}_r\middle|\sigma\!\left(\Xi^{\prime}_{N_0^c}\right)\right){\succeq} {\epsilon}^2K_{\epsilon}\star \delta_U\right\} \\ &\ge \sup_{U\in \sigma\!\left(\Xi_{N_0^c},\Xi^{\prime}_{N_0^c}\right)}\mathbb{P}\!\left\{\tilde{\xi}\star\tilde{\xi}^{\prime}{\succeq} {\epsilon}^2K_{\epsilon}\star \delta_U \right\}\\ &\ge 2p^2,\end{align*}
\begin{align*} &\sup_{U\in \sigma\!\left(\Xi_{B(N_0,2r)\backslash N_0},\Xi^{\prime}_{B(N_0,2r)\backslash N_0}\right)}\begin{aligned} \mathbb{P}&\left\{\mathscr{L}\!\left(Y_r\middle|\sigma\!\left(\Xi_{B(N_0,2r)\backslash N_0}\right)\right)\star\mathscr{L}\!\left(Y^{\prime}_r\middle|\sigma\!\left(\Xi^{\prime}_{B(N_0,2r)\backslash N_0}\right)\right)\right.\\ &\left.{\succeq} {\epsilon}^2K_{\epsilon}\star \delta_U\right\} \end{aligned} \\ &=\sup_{U\in \sigma\!\left(\Xi_{N_0^c},\Xi^{\prime}_{N_0^c}\right)} \mathbb{P}\!\left\{\mathscr{L}\!\left(Y_r\middle|\sigma\!\left(\Xi_{B(N_0,2r)\backslash N_0}\right)\right)\star\mathscr{L}\!\left(Y^{\prime}_r\middle|\sigma\!\left(\Xi^{\prime}_{B(N_0,2r)\backslash N_0}\right)\right){\succeq} {\epsilon}^2K_{\epsilon}\star \delta_U\right\} \\ &= \sup_{U\in \sigma\!\left(\Xi_{N_0^c},\Xi^{\prime}_{N_0^c}\right)}\mathbb{P}\!\left\{\mathscr{L}\!\left(Y_r\middle|\sigma\!\left(\Xi_{N_0^c}\right)\right)\star\mathscr{L}\!\left(Y^{\prime}_r\middle|\sigma\!\left(\Xi^{\prime}_{N_0^c}\right)\right){\succeq} {\epsilon}^2K_{\epsilon}\star \delta_U\right\} \\ &\ge \sup_{U\in \sigma\!\left(\Xi_{N_0^c},\Xi^{\prime}_{N_0^c}\right)}\mathbb{P}\!\left\{\tilde{\xi}\star\tilde{\xi}^{\prime}{\succeq} {\epsilon}^2K_{\epsilon}\star \delta_U \right\}\\ &\ge 2p^2,\end{align*}
which ensures that, for any
![]() $r>R_0$
, we can find a
$r>R_0$
, we can find a
![]() $\sigma\!\left(\Xi_{B(N_0,2r)\backslash N_0},\Xi^{\prime}_{B(N_0,2r)\backslash N_0}\right)$
-measurable U such that
$\sigma\!\left(\Xi_{B(N_0,2r)\backslash N_0},\Xi^{\prime}_{B(N_0,2r)\backslash N_0}\right)$
-measurable U such that
If
![]() $\alpha\le (2(4r+2r_1))^d$
, (4.4) is trivial with
$\alpha\le (2(4r+2r_1))^d$
, (4.4) is trivial with
so we now assume
![]() $\alpha> \{2(4r+2r_1)\}^d$
. From the structure of
$\alpha> \{2(4r+2r_1)\}^d$
. From the structure of
![]() $\Xi$
, we can see that
$\Xi$
, we can see that
![]() $\Xi(A,D)\overset{d}{=}\Xi(x+A,D)$
, and
$\Xi(A,D)\overset{d}{=}\Xi(x+A,D)$
, and
![]() $\Xi(A,D)$
is independent of
$\Xi(A,D)$
is independent of
![]() $\Xi(B,D)$
for all disjoint
$\Xi(B,D)$
for all disjoint
![]() $A, B\in\mathscr{B}\big(\mathbb{R}^d\big)$
,
$A, B\in\mathscr{B}\big(\mathbb{R}^d\big)$
,
![]() $D\in \mathscr{T}$
, and
$D\in \mathscr{T}$
, and
![]() $x\in \mathbb{R}^d$
. For a fixed
$x\in \mathbb{R}^d$
. For a fixed
![]() $r>R_0$
, we can divide
$r>R_0$
, we can divide
![]() $\Gamma_\alpha$
into disjoint cubes
$\Gamma_\alpha$
into disjoint cubes
![]() $\mathbb{C}_1,\cdots,\mathbb{C}_{m_{\alpha,r}}$
with edge length
$\mathbb{C}_1,\cdots,\mathbb{C}_{m_{\alpha,r}}$
with edge length
![]() $4r+2r_1$
and centres
$4r+2r_1$
and centres
![]() $c_1$
,
$c_1$
,
![]() $\cdots$
,
$\cdots$
,
![]() $c_{m_{\alpha,r}}$
, aiming to maximise the number of cubes, so
$c_{m_{\alpha,r}}$
, aiming to maximise the number of cubes, so
![]() $m_{\alpha,r}\sim \alpha(4r+2r_1)^{-d}$
, which has order
$m_{\alpha,r}\sim \alpha(4r+2r_1)^{-d}$
, which has order
![]() $\mathop{{}\textrm{O}}\mathopen{}\big(\alpha r^{-d}\big)$
. Without loss of generality, we can assume that
$\mathop{{}\textrm{O}}\mathopen{}\big(\alpha r^{-d}\big)$
. Without loss of generality, we can assume that
![]() $m_{\alpha,r}$
is even or simply delete one of them, and the above properties still hold. For
$m_{\alpha,r}$
is even or simply delete one of them, and the above properties still hold. For
![]() $i\le m_{\alpha,r}$
, we define
$i\le m_{\alpha,r}$
, we define
 \begin{align*}A_i&=c_i+N_0, \qquad B_i=B(A_i,r), \qquad C_i=B(B_i,r), \qquad D_i=C_i\backslash A_i,\\{\mathcal{N}}_{0,\alpha,r}&\,:\!=\,\cup_{1\le i\le m_{\alpha,r}}A_i, \qquad {\mathcal{N}}_{1,\alpha,r}\,:\!=\,\cup_{1\le i\le m_{\alpha,r}}B_i, \qquad {\mathcal{N}}_{2,\alpha,r}\,:\!=\,\cup_{1\le i\le m_{\alpha,r}} D_i,\\{\mathscr{F}}_{1,\alpha,r}&\,:\!=\,\sigma\big(\Xi_{\mathbb{R}^d\backslash {\mathcal{N}}_{0,\alpha,r}}\big), \qquad {\mathscr{F}}_{2,\alpha,r}\,:\!=\,\sigma\big(\Xi_{ {\mathcal{N}}_{2,\alpha,r}}\big),\\W_{\alpha,r}^0&=\int_{{\mathcal{N}}_{1,\alpha,r}}\bar{g}(\Xi^{x})\textbf{1}_{R(x)<r}\bar{\Xi}(dx), \qquad W_{\alpha,r}^1=W_{\alpha,r}-W_{\alpha,r}^0.\end{align*}
\begin{align*}A_i&=c_i+N_0, \qquad B_i=B(A_i,r), \qquad C_i=B(B_i,r), \qquad D_i=C_i\backslash A_i,\\{\mathcal{N}}_{0,\alpha,r}&\,:\!=\,\cup_{1\le i\le m_{\alpha,r}}A_i, \qquad {\mathcal{N}}_{1,\alpha,r}\,:\!=\,\cup_{1\le i\le m_{\alpha,r}}B_i, \qquad {\mathcal{N}}_{2,\alpha,r}\,:\!=\,\cup_{1\le i\le m_{\alpha,r}} D_i,\\{\mathscr{F}}_{1,\alpha,r}&\,:\!=\,\sigma\big(\Xi_{\mathbb{R}^d\backslash {\mathcal{N}}_{0,\alpha,r}}\big), \qquad {\mathscr{F}}_{2,\alpha,r}\,:\!=\,\sigma\big(\Xi_{ {\mathcal{N}}_{2,\alpha,r}}\big),\\W_{\alpha,r}^0&=\int_{{\mathcal{N}}_{1,\alpha,r}}\bar{g}(\Xi^{x})\textbf{1}_{R(x)<r}\bar{\Xi}(dx), \qquad W_{\alpha,r}^1=W_{\alpha,r}-W_{\alpha,r}^0.\end{align*}
Note that for all x such that
![]() $d(x,\partial \Gamma_\alpha)\ge r$
,
$d(x,\partial \Gamma_\alpha)\ge r$
,
for all
![]() $(x,m)\in \Xi$
a.s. From the definition of total variation distance,
$(x,m)\in \Xi$
a.s. From the definition of total variation distance,
hence the tower property ensures that
 \begin{align} &\quad d_{TV}\!\left(W_{\alpha,r},W_{\alpha,r}+\gamma\right)\nonumber \\&=\sup_{A\in \mathscr{B}(\mathbb{R})}\mathbb{E}\!\left(\textbf{1}_{W_{\alpha,r}\in A}-\textbf{1}_{W_{\alpha,r}\in A-\gamma}\right)\nonumber \\&=\sup_{A\in \mathscr{B}(\mathbb{R})}\mathbb{E}\!\left(\mathbb{E}\!\left(\textbf{1}_{W_{\alpha,r}\in A}-\textbf{1}_{W_{\alpha,r}\in A-\gamma}|\mathscr{F}_{1,\alpha,r}\right)\right)\nonumber \\&=\sup_{A\in \mathscr{B}(\mathbb{R})}\mathbb{E}\!\left(\mathbb{E}\!\left(\textbf{1}_{W_{\alpha,r}^0\in A-W_{\alpha,r}^1}-\textbf{1}_{W_{\alpha,r}^0\in A-\gamma-W_{\alpha,r}^1}|\mathscr{F}_{1,\alpha,r}\right)\right)\nonumber \\&\le \mathbb{E}\!\left(\sup_{A\in \mathscr{B}(\mathbb{R})}\left[\mathbb{E}\!\left(\textbf{1}_{W_{\alpha,r}^0\in A}-\textbf{1}_{W_{\alpha,r}^0\in A-\gamma}|\mathscr{F}_{1,\alpha,r}\right)\right]\right)\nonumber \\&=\mathbb{E}\!\left(\sup_{A\in \mathscr{B}(\mathbb{R})}\left[\mathbb{E}\!\left(\textbf{1}_{W_{\alpha,r}^0\in A}-\textbf{1}_{W_{\alpha,r}^0\in A-\gamma}|\mathscr{F}_{2,\alpha,r}\right)\right]\right),\end{align}
\begin{align} &\quad d_{TV}\!\left(W_{\alpha,r},W_{\alpha,r}+\gamma\right)\nonumber \\&=\sup_{A\in \mathscr{B}(\mathbb{R})}\mathbb{E}\!\left(\textbf{1}_{W_{\alpha,r}\in A}-\textbf{1}_{W_{\alpha,r}\in A-\gamma}\right)\nonumber \\&=\sup_{A\in \mathscr{B}(\mathbb{R})}\mathbb{E}\!\left(\mathbb{E}\!\left(\textbf{1}_{W_{\alpha,r}\in A}-\textbf{1}_{W_{\alpha,r}\in A-\gamma}|\mathscr{F}_{1,\alpha,r}\right)\right)\nonumber \\&=\sup_{A\in \mathscr{B}(\mathbb{R})}\mathbb{E}\!\left(\mathbb{E}\!\left(\textbf{1}_{W_{\alpha,r}^0\in A-W_{\alpha,r}^1}-\textbf{1}_{W_{\alpha,r}^0\in A-\gamma-W_{\alpha,r}^1}|\mathscr{F}_{1,\alpha,r}\right)\right)\nonumber \\&\le \mathbb{E}\!\left(\sup_{A\in \mathscr{B}(\mathbb{R})}\left[\mathbb{E}\!\left(\textbf{1}_{W_{\alpha,r}^0\in A}-\textbf{1}_{W_{\alpha,r}^0\in A-\gamma}|\mathscr{F}_{1,\alpha,r}\right)\right]\right)\nonumber \\&=\mathbb{E}\!\left(\sup_{A\in \mathscr{B}(\mathbb{R})}\left[\mathbb{E}\!\left(\textbf{1}_{W_{\alpha,r}^0\in A}-\textbf{1}_{W_{\alpha,r}^0\in A-\gamma}|\mathscr{F}_{2,\alpha,r}\right)\right]\right),\end{align}
where the last equality follows from the fact that
![]() $W_{\alpha,r}^0$
depends on
$W_{\alpha,r}^0$
depends on
![]() ${\mathscr{F}}_{2,\alpha,r}$
in
${\mathscr{F}}_{2,\alpha,r}$
in
![]() ${\mathscr{F}}_{1,\alpha,r}$
.
${\mathscr{F}}_{1,\alpha,r}$
.
From (5.19), to show (4.4), it is sufficient to show that
 \begin{equation*}\mathbb{E}\!\left(\sup_{A\in \mathscr{B}(\mathbb{R})}\left[\mathbb{E}\!\left(\textbf{1}_{W_{\alpha,r}^0\in A}-\textbf{1}_{W_{\alpha,r}^0\in A-\gamma}|{\mathscr{F}}_{2,\alpha,r}\right)\right]\right)\le (|\gamma|\vee 1)\mathop{{}\textrm{O}}\mathopen{}\left(\alpha^{-\frac{1}{2}}r^{\frac{d}{2}}\right).\end{equation*}
\begin{equation*}\mathbb{E}\!\left(\sup_{A\in \mathscr{B}(\mathbb{R})}\left[\mathbb{E}\!\left(\textbf{1}_{W_{\alpha,r}^0\in A}-\textbf{1}_{W_{\alpha,r}^0\in A-\gamma}|{\mathscr{F}}_{2,\alpha,r}\right)\right]\right)\le (|\gamma|\vee 1)\mathop{{}\textrm{O}}\mathopen{}\left(\alpha^{-\frac{1}{2}}r^{\frac{d}{2}}\right).\end{equation*}
Using the fact that
![]() $\int_{B_i} \bar{g}(\Xi^{x})\textbf{1}_{R(x)<r}\overline{\Xi}(dx)$
depends only on
$\int_{B_i} \bar{g}(\Xi^{x})\textbf{1}_{R(x)<r}\overline{\Xi}(dx)$
depends only on
![]() $\sigma(\Xi_{D_i})$
in
$\sigma(\Xi_{D_i})$
in
![]() ${\mathscr{F}}_{2,\alpha,r}$
for
${\mathscr{F}}_{2,\alpha,r}$
for
![]() $i\le m_{\alpha,r} $
, and from the independence of
$i\le m_{\alpha,r} $
, and from the independence of
![]() $\sigma(\Xi_{D_i})$
for different i, we can see that
$\sigma(\Xi_{D_i})$
for different i, we can see that
 \begin{align} \mathscr{L}\!\left(W_{\alpha,r}^0|{\mathscr{F}}_{2,\alpha,r}\right)&=\mathscr{L}\!\left(\sum_{i=1}^{m_{\alpha,r}}\left.\int_{B_i} \bar{g}(\Xi^{x})\textbf{1}_{R(x)<r}\overline{\Xi}(dx)\right|{\mathscr{F}}_{2,\alpha,r}\right)\nonumber \\&=\mathscr{L}\!\left(\left.\sum_{i=1}^{m_{\alpha,r}}\int_{B_i} \bar{g}(\Xi^{x})\textbf{1}_{R(x)<r}\overline{\Xi}(dx)\right|\sigma\!\left(\Xi_{D_i}, i\le m_{\alpha,r}\right)\right). \end{align}
\begin{align} \mathscr{L}\!\left(W_{\alpha,r}^0|{\mathscr{F}}_{2,\alpha,r}\right)&=\mathscr{L}\!\left(\sum_{i=1}^{m_{\alpha,r}}\left.\int_{B_i} \bar{g}(\Xi^{x})\textbf{1}_{R(x)<r}\overline{\Xi}(dx)\right|{\mathscr{F}}_{2,\alpha,r}\right)\nonumber \\&=\mathscr{L}\!\left(\left.\sum_{i=1}^{m_{\alpha,r}}\int_{B_i} \bar{g}(\Xi^{x})\textbf{1}_{R(x)<r}\overline{\Xi}(dx)\right|\sigma\!\left(\Xi_{D_i}, i\le m_{\alpha,r}\right)\right). \end{align}
Using (5.18), we obtain
 \begin{align*} &\mathscr{L}\!\left(\left.\sum_{i=2j-1}^{2j}\int_{B_i} \bar{g}(\Xi^{x})\textbf{1}_{R(x)<r}\overline{\Xi}(dx)\right|\sigma\!\left(\Xi_{D_i}, i\le m_{\alpha,r}\right)\right)\\ &=\mathscr{L}\!\left(\left.X_{1,j}\left(1-J_{1,j}\right)+X_{2,j}J_{1,j}\left(1-J_{2,j}\right)+(X_{3,j}+U_j)J_{1,j}J_{2,j}\right|\sigma\!\left(\Xi_{D_{2j-1}}, \Xi_{D_{2j}}\right)\right),\end{align*}
\begin{align*} &\mathscr{L}\!\left(\left.\sum_{i=2j-1}^{2j}\int_{B_i} \bar{g}(\Xi^{x})\textbf{1}_{R(x)<r}\overline{\Xi}(dx)\right|\sigma\!\left(\Xi_{D_i}, i\le m_{\alpha,r}\right)\right)\\ &=\mathscr{L}\!\left(\left.X_{1,j}\left(1-J_{1,j}\right)+X_{2,j}J_{1,j}\left(1-J_{2,j}\right)+(X_{3,j}+U_j)J_{1,j}J_{2,j}\right|\sigma\!\left(\Xi_{D_{2j-1}}, \Xi_{D_{2j}}\right)\right),\end{align*}
where
![]() $J_{1,j}$
,
$J_{1,j}$
,
![]() $J_{2,j}$
and
$J_{2,j}$
and
![]() $U_j$
are
$U_j$
are
![]() $\sigma\!\left(\Xi_{D_{2j-1}}, \Xi_{D_{2j}}\right)$
-measurable with
$\sigma\!\left(\Xi_{D_{2j-1}}, \Xi_{D_{2j}}\right)$
-measurable with
![]() $\mathbb{P}(J_{1,j}=1)=1-\mathbb{P}(J_{1,j}=0)=p^2$
,
$\mathbb{P}(J_{1,j}=1)=1-\mathbb{P}(J_{1,j}=0)=p^2$
,
![]() $\mathbb{P}(J_{2,j}=1)=1-\mathbb{P}(J_{2,j}=0)={\epsilon}^2$
,
$\mathbb{P}(J_{2,j}=1)=1-\mathbb{P}(J_{2,j}=0)={\epsilon}^2$
,
![]() $J_{1,j} \perp \!\!\! \perp J_{2,j}$
,
$J_{1,j} \perp \!\!\! \perp J_{2,j}$
,
![]() $X_{1,j} $
and
$X_{1,j} $
and
![]() $X_{2,j} $
are
$X_{2,j} $
are
![]() $\sigma\!\left(\Xi_{B_{2j-1}}, \Xi_{B_{2j}}\right)$
-measurable, and
$\sigma\!\left(\Xi_{B_{2j-1}}, \Xi_{B_{2j}}\right)$
-measurable, and
![]() $X_{3,j}\sim K_{\epsilon},\ 1\le j\le m_{\alpha,r}/2,$
are i.i.d. and independent of
$X_{3,j}\sim K_{\epsilon},\ 1\le j\le m_{\alpha,r}/2,$
are i.i.d. and independent of
![]() $\sigma\!\left(\Xi_{D_i}, i\le m_{\alpha,r}\right)$
. Define
$\sigma\!\left(\Xi_{D_i}, i\le m_{\alpha,r}\right)$
. Define
 \begin{align*}\Sigma_1&\,:\!=\, \sum_{j=1}^{m_{\alpha,r}/2}\big(X_{1,j}\left(1-J_{1,j}\right)+X_{2,j}J_{1,j}\left(1-J_{2,j}\right)+\big(X_{3,j}+U_j\big)J_{1,j}J_{2,j}\big),\\\Sigma_2&\,:\!=\, \sum_{j=1}^{m_{\alpha,r}/2}X_{3,j}J_{1,j}J_{2,j},\\\Sigma_{3,l}&\,:\!=\, \sum_{j=1}^lX_{3,j},\end{align*}
\begin{align*}\Sigma_1&\,:\!=\, \sum_{j=1}^{m_{\alpha,r}/2}\big(X_{1,j}\left(1-J_{1,j}\right)+X_{2,j}J_{1,j}\left(1-J_{2,j}\right)+\big(X_{3,j}+U_j\big)J_{1,j}J_{2,j}\big),\\\Sigma_2&\,:\!=\, \sum_{j=1}^{m_{\alpha,r}/2}X_{3,j}J_{1,j}J_{2,j},\\\Sigma_{3,l}&\,:\!=\, \sum_{j=1}^lX_{3,j},\end{align*}
and let
![]() $I\sim$
Binomial
$I\sim$
Binomial
![]() $\big(m_{\alpha,r}/2,{\epsilon}^2p^2\big)$
be independent of
$\big(m_{\alpha,r}/2,{\epsilon}^2p^2\big)$
be independent of
![]() $\big\{X_{3,j}\,:\,j\le m_{\alpha,r}/2\big\}$
. It follows from (5.19) and (5.20) that
$\big\{X_{3,j}\,:\,j\le m_{\alpha,r}/2\big\}$
. It follows from (5.19) and (5.20) that
 \begin{align} & \quad d_{TV}\!\left(W_{\alpha,r},W_{\alpha,r}+\gamma\right)\nonumber \\ &\le \mathbb{E}\!\left(\sup_{A\in \mathscr{B}(\mathbb{R})}\left[\mathbb{E}\!\left(\textbf{1}_{\Sigma_1\in A}-\textbf{1}_{\Sigma_1\in A-\gamma}|\sigma\!\left(\Xi_{D_i}, i\le m_{\alpha,r}\right)\right)\right]\right)\nonumber \\ &\le \mathbb{E}\!\left(\sup_{A\in \mathscr{B}(\mathbb{R})}\left[\mathbb{E}\!\left(\textbf{1}_{\Sigma_2\in A}-\textbf{1}_{\Sigma_2\in A-\gamma}|\sigma\!\left(\Xi_{D_i}, i\le m_{\alpha,r}\right)\right)\right]\right)\nonumber \\ &=\mathbb{E}\!\left(\sup_{A\in \mathscr{B}(\mathbb{R})}\left[\mathbb{E}\!\left(\textbf{1}_{\Sigma_{3,I}\in A}-\textbf{1}_{\Sigma_{3,I}\in A-\gamma}|I\right)\right]\right)\nonumber \\&\le \mathbb{P}(I\le (\mathbb{E} I)/2)+\sum_{(\mathbb{E} I)/2<j\le m_{\alpha,r}/2}\sup_{A\in \mathscr{B}(\mathbb{R})}\left[\mathbb{E}\!\left(\textbf{1}_{\Sigma_{3,j}\in A}-\textbf{1}_{\Sigma_{3,j}\in A-\gamma}\right)\right]\mathbb{P}(I=j)\nonumber \\&\le \mathop{{}\textrm{O}}\mathopen{}\left(\alpha^{-1}r^d\right)+\mathop{{}\textrm{O}}\mathopen{}\left(\alpha^{-\frac{1}{2}}r^{\frac{d}{2}}\right)|\gamma|= \left(|\gamma|\vee 1\right)\mathop{{}\textrm{O}}\mathopen{}\left(\alpha^{-\frac{1}{2}}r^{\frac{d}{2}}\right),\end{align}
\begin{align} & \quad d_{TV}\!\left(W_{\alpha,r},W_{\alpha,r}+\gamma\right)\nonumber \\ &\le \mathbb{E}\!\left(\sup_{A\in \mathscr{B}(\mathbb{R})}\left[\mathbb{E}\!\left(\textbf{1}_{\Sigma_1\in A}-\textbf{1}_{\Sigma_1\in A-\gamma}|\sigma\!\left(\Xi_{D_i}, i\le m_{\alpha,r}\right)\right)\right]\right)\nonumber \\ &\le \mathbb{E}\!\left(\sup_{A\in \mathscr{B}(\mathbb{R})}\left[\mathbb{E}\!\left(\textbf{1}_{\Sigma_2\in A}-\textbf{1}_{\Sigma_2\in A-\gamma}|\sigma\!\left(\Xi_{D_i}, i\le m_{\alpha,r}\right)\right)\right]\right)\nonumber \\ &=\mathbb{E}\!\left(\sup_{A\in \mathscr{B}(\mathbb{R})}\left[\mathbb{E}\!\left(\textbf{1}_{\Sigma_{3,I}\in A}-\textbf{1}_{\Sigma_{3,I}\in A-\gamma}|I\right)\right]\right)\nonumber \\&\le \mathbb{P}(I\le (\mathbb{E} I)/2)+\sum_{(\mathbb{E} I)/2<j\le m_{\alpha,r}/2}\sup_{A\in \mathscr{B}(\mathbb{R})}\left[\mathbb{E}\!\left(\textbf{1}_{\Sigma_{3,j}\in A}-\textbf{1}_{\Sigma_{3,j}\in A-\gamma}\right)\right]\mathbb{P}(I=j)\nonumber \\&\le \mathop{{}\textrm{O}}\mathopen{}\left(\alpha^{-1}r^d\right)+\mathop{{}\textrm{O}}\mathopen{}\left(\alpha^{-\frac{1}{2}}r^{\frac{d}{2}}\right)|\gamma|= \left(|\gamma|\vee 1\right)\mathop{{}\textrm{O}}\mathopen{}\left(\alpha^{-\frac{1}{2}}r^{\frac{d}{2}}\right),\end{align}
where the first term of (5.21) is from Chebyshev’s inequality, and the second term is due to Lemma 4.1. This completes the proof of (4.4).
In terms of (4.5), since range-boundedness implies polynomial stabilisation with arbitrary order
![]() $\beta$
, (4.4) still holds for all
$\beta$
, (4.4) still holds for all
![]() $r>R_0$
. On the other hand,
$r>R_0$
. On the other hand,
![]() $\bar{W}_\alpha=\bar{W}_{\alpha,r}$
a.s. when
$\bar{W}_\alpha=\bar{W}_{\alpha,r}$
a.s. when
![]() $r>t$
for some positive constant t; (4.5) follows by taking
$r>t$
for some positive constant t; (4.5) follows by taking
![]() $r=R_0\vee t+1$
.
$r=R_0\vee t+1$
.
The claim (4.6) can be proved by replacing
![]() $W_\alpha$
with
$W_\alpha$
with
![]() $\bar{W}_\alpha$
,
$\bar{W}_\alpha$
,
![]() $W_{\alpha,r}$
with
$W_{\alpha,r}$
with
![]() $\bar{W}_{\alpha,r}$
,
$\bar{W}_{\alpha,r}$
,
![]() $\bar{g}$
with g,
$\bar{g}$
with g,
![]() $W^0_{\alpha,r}$
with
$W^0_{\alpha,r}$
with
![]() $\bar{W}^0_{\alpha,r}$
,
$\bar{W}^0_{\alpha,r}$
,
![]() $W^1_{\alpha,r}$
with
$W^1_{\alpha,r}$
with
![]() $\bar{W}^1_{\alpha,r}$
,
$\bar{W}^1_{\alpha,r}$
,
![]() $\Xi^{x}$
by
$\Xi^{x}$
by
![]() $\Xi^{\Gamma_\alpha,x}$
, R(x) with
$\Xi^{\Gamma_\alpha,x}$
, R(x) with
![]() $\bar{R}(x,\alpha)$
, and
$\bar{R}(x,\alpha)$
, and
![]() $R\big(x,{M_1},\Xi+\delta_{(x, {M_1})}\big)$
with
$R\big(x,{M_1},\Xi+\delta_{(x, {M_1})}\big)$
with
![]() $\bar{R}\big(x,{M_1},\alpha,\Xi+\delta_{(x, {M_1})}\big)$
, and redefining
$\bar{R}\big(x,{M_1},\alpha,\Xi+\delta_{(x, {M_1})}\big)$
, and redefining
![]() ${\mathscr{F}}_{1,\alpha,r}\,:\!=\,\sigma\big(\Xi_{\Gamma_\alpha\backslash {\mathcal{N}}_{0,\alpha,r}}\big)$
. The bound (4.7) can be argued in the same way as that for (4.5).
${\mathscr{F}}_{1,\alpha,r}\,:\!=\,\sigma\big(\Xi_{\Gamma_\alpha\backslash {\mathcal{N}}_{0,\alpha,r}}\big)$
. The bound (4.7) can be argued in the same way as that for (4.5).
Proof of Corollary
4.1. The proof can easily be adapted from the second half of the proof of Lemma 4.4, and we start with (4.9). If
![]() $\alpha^{-\frac{1}{d}}(1-2q)^{-1}(4r+2r_1)>\frac{1}{3}$
, (4.9) is obvious because the total variation distance is bounded above by 1. Now we assume
$\alpha^{-\frac{1}{d}}(1-2q)^{-1}(4r+2r_1)>\frac{1}{3}$
, (4.9) is obvious because the total variation distance is bounded above by 1. Now we assume
![]() $\alpha^{-\frac{1}{d}}(1-2q)^{-1}(4r+2r_1)\le\frac{1}{3}$
. Similarly to the proof of Lemma 4.4, we embed disjoint cubes with edge length
$\alpha^{-\frac{1}{d}}(1-2q)^{-1}(4r+2r_1)\le\frac{1}{3}$
. Similarly to the proof of Lemma 4.4, we embed disjoint cubes with edge length
![]() $4r+2r_1$
into
$4r+2r_1$
into
![]() $\Gamma_\alpha\backslash \left(N_{\alpha,r}^{(1)}\cup N_{\alpha,r}^{(2)}\cup N_{\alpha,r}^{(3)}\right)$
, aiming to maximise the number
$\Gamma_\alpha\backslash \left(N_{\alpha,r}^{(1)}\cup N_{\alpha,r}^{(2)}\cup N_{\alpha,r}^{(3)}\right)$
, aiming to maximise the number
![]() $m_{\alpha,r}$
of cubes. Without loss of generality, we assume that
$m_{\alpha,r}$
of cubes. Without loss of generality, we assume that
![]() $m_{\alpha,r}$
is even. Then we have
$m_{\alpha,r}$
is even. Then we have
giving
![]() $m_{\alpha,r}=\mathop{{}\textrm{O}}\mathopen{}\big(\alpha r^{-d}\big)$
.
$m_{\alpha,r}=\mathop{{}\textrm{O}}\mathopen{}\big(\alpha r^{-d}\big)$
.
We use the same notation as in the proof of Lemma 4.4 but with
![]() $\Gamma_\alpha$
replaced by
$\Gamma_\alpha$
replaced by
![]() $\Gamma_\alpha\backslash\Big(N_{\alpha,r}^{(1)}\cup N_{\alpha,r}^{(2)}\cup N_{\alpha,r}^{(3)}\Big)$
, and define
$\Gamma_\alpha\backslash\Big(N_{\alpha,r}^{(1)}\cup N_{\alpha,r}^{(2)}\cup N_{\alpha,r}^{(3)}\Big)$
, and define
Bearing in mind that
![]() $N_{\alpha,r}^{(1)}\cup N_{\alpha,r}^{(2)}\cup N_{\alpha,r}^{(3)}$
is excluded from the
$N_{\alpha,r}^{(1)}\cup N_{\alpha,r}^{(2)}\cup N_{\alpha,r}^{(3)}$
is excluded from the
![]() $m_{\alpha,r}$
cubes, we have
$m_{\alpha,r}$
cubes, we have
![]() $\mathscr{F}_{0,\alpha,r}\subset \mathscr{F}_{1,\alpha,r}$
, giving the following result analogous to (5.19):
$\mathscr{F}_{0,\alpha,r}\subset \mathscr{F}_{1,\alpha,r}$
, giving the following result analogous to (5.19):
 \begin{align*} & \quad d_{TV}\!\left(\bar{W}^{\prime}_{\alpha,r},\bar{W}^{\prime}_{\alpha,r}+h_{\alpha,r}\left(\Xi_{N_{\alpha, r}^{(2)}}\right)\middle|\mathscr{F}_{0,\alpha,r}\right) \\&=\sup_{A\in \mathscr{B}(\mathbb{R})}\mathbb{E}\!\left(\textbf{1}_{\bar{W}^{\prime}_{\alpha,r}\in A}-\textbf{1}_{\bar{W}_{\alpha,r}\in A-h_{\alpha,r}\left(\Xi_{N_{\alpha, r}^{(2)}}\right)}\middle|\mathscr{F}_{0,\alpha,r}\right) \\&=\sup_{A\in \mathscr{B}(\mathbb{R})}\mathbb{E}\!\left(\mathbb{E}\!\left(\textbf{1}_{\bar{W}_{\alpha,r}\in A}-\textbf{1}_{\bar{W}_{\alpha,r}\in A-h_{\alpha,r}\left(\Xi_{N_{\alpha, r}^{(2)}}\right)}\middle|\mathscr{F}_{1,\alpha,r}\right)\middle|\mathscr{F}_{0,\alpha,r}\right) \\&=\sup_{A\in \mathscr{B}(\mathbb{R})}\mathbb{E}\!\left(\mathbb{E}\!\left(\textbf{1}_{\bar{W}_{\alpha,r}^0\in A}-\textbf{1}_{\bar{W}_{\alpha,r}^0\in A-h_{\alpha,r}\left(\Xi_{N_{\alpha, r}^{(2)}}\right)}\middle|\mathscr{F}_{1,\alpha,r}\right)\middle|\mathscr{F}_{0,\alpha,r}\right) \\&\le \mathbb{E}\!\left(\sup_{A\in \mathscr{B}(\mathbb{R})}\left[\mathbb{E}\!\left(\textbf{1}_{\bar{W}_{\alpha,r}^0\in A}-\textbf{1}_{\bar{W}_{\alpha,r}^0\in A-h_{\alpha,r}\left(\Xi_{N_{\alpha, r}^{(2)}}\right)}\middle|\mathscr{F}_{1,\alpha,r}\right)\right]\middle|\mathscr{F}_{0,\alpha,r}\right) \\ &=\mathbb{E}\!\left(\sup_{A\in \mathscr{B}(\mathbb{R})}\left[\mathbb{E}\!\left(\textbf{1}_{\bar{W}_{\alpha,r}^0\in A}-\textbf{1}_{\bar{W}_{\alpha,r}^0\in A-h_{\alpha,r}\left(\Xi_{N_{\alpha, r}^{(2)}}\right)}\middle|\mathscr{F}^{\prime}_{2,\alpha,r}\right)\right]\middle|\mathscr{F}_{0,\alpha,r}\right).\end{align*}
\begin{align*} & \quad d_{TV}\!\left(\bar{W}^{\prime}_{\alpha,r},\bar{W}^{\prime}_{\alpha,r}+h_{\alpha,r}\left(\Xi_{N_{\alpha, r}^{(2)}}\right)\middle|\mathscr{F}_{0,\alpha,r}\right) \\&=\sup_{A\in \mathscr{B}(\mathbb{R})}\mathbb{E}\!\left(\textbf{1}_{\bar{W}^{\prime}_{\alpha,r}\in A}-\textbf{1}_{\bar{W}_{\alpha,r}\in A-h_{\alpha,r}\left(\Xi_{N_{\alpha, r}^{(2)}}\right)}\middle|\mathscr{F}_{0,\alpha,r}\right) \\&=\sup_{A\in \mathscr{B}(\mathbb{R})}\mathbb{E}\!\left(\mathbb{E}\!\left(\textbf{1}_{\bar{W}_{\alpha,r}\in A}-\textbf{1}_{\bar{W}_{\alpha,r}\in A-h_{\alpha,r}\left(\Xi_{N_{\alpha, r}^{(2)}}\right)}\middle|\mathscr{F}_{1,\alpha,r}\right)\middle|\mathscr{F}_{0,\alpha,r}\right) \\&=\sup_{A\in \mathscr{B}(\mathbb{R})}\mathbb{E}\!\left(\mathbb{E}\!\left(\textbf{1}_{\bar{W}_{\alpha,r}^0\in A}-\textbf{1}_{\bar{W}_{\alpha,r}^0\in A-h_{\alpha,r}\left(\Xi_{N_{\alpha, r}^{(2)}}\right)}\middle|\mathscr{F}_{1,\alpha,r}\right)\middle|\mathscr{F}_{0,\alpha,r}\right) \\&\le \mathbb{E}\!\left(\sup_{A\in \mathscr{B}(\mathbb{R})}\left[\mathbb{E}\!\left(\textbf{1}_{\bar{W}_{\alpha,r}^0\in A}-\textbf{1}_{\bar{W}_{\alpha,r}^0\in A-h_{\alpha,r}\left(\Xi_{N_{\alpha, r}^{(2)}}\right)}\middle|\mathscr{F}_{1,\alpha,r}\right)\right]\middle|\mathscr{F}_{0,\alpha,r}\right) \\ &=\mathbb{E}\!\left(\sup_{A\in \mathscr{B}(\mathbb{R})}\left[\mathbb{E}\!\left(\textbf{1}_{\bar{W}_{\alpha,r}^0\in A}-\textbf{1}_{\bar{W}_{\alpha,r}^0\in A-h_{\alpha,r}\left(\Xi_{N_{\alpha, r}^{(2)}}\right)}\middle|\mathscr{F}^{\prime}_{2,\alpha,r}\right)\right]\middle|\mathscr{F}_{0,\alpha,r}\right).\end{align*}
The rest is a line-by-line repetition of the proof of Lemma 4.4 with
![]() $\gamma$
replaced by
$\gamma$
replaced by
![]() $h_{\alpha,r}\left(\Xi_{N_{\alpha, r}^{(2)}}\right)$
, and the expectations replaced by the conditional expectations given
$h_{\alpha,r}\left(\Xi_{N_{\alpha, r}^{(2)}}\right)$
, and the expectations replaced by the conditional expectations given
![]() $\mathscr{F}_{0,\alpha,r}$
, leading to
$\mathscr{F}_{0,\alpha,r}$
, leading to
 \begin{align} & \quad d_{TV}\!\left(\bar{W}^{\prime}_{\alpha,r},\bar{W}^{\prime}_{\alpha,r}+h_{\alpha,r}\left(\Xi_{N_{\alpha, r}^{(2)}}\right)\middle|\mathscr{F}_{0,\alpha,r}\right)\nonumber \\&\le \mathbb{E}\!\left(\sup_{A\in \mathscr{B}(\mathbb{R})}\left[\mathbb{E}\!\left(\textbf{1}_{\bar{W}_{\alpha,r}^0\in A}-\textbf{1}_{\bar{W}_{\alpha,r}^0\in A-h_{\alpha,r}\left(\Xi_{N_{\alpha, r}^{(2)}}\right)}\middle|\mathscr{F}^{\prime}_{2,\alpha,r}\right)\right]\middle|\mathscr{F}_{0,\alpha,r}\right)\nonumber \\&\le \mathbb{E}\!\left(\mathbb{E}\!\left[\sup_{A\in \mathscr{B}(\mathbb{R})}\left(\textbf{1}_{{\Sigma_{3,I}}\in A}-\textbf{1}_{{\Sigma_{3,I}}\in A-h_{\alpha,r}\left(\Xi_{N_{\alpha, r}^{(2)}}\right)}\middle|I,\sigma\!\left(\Xi_{N_{\alpha,r}^{(2)}}\right)\right)\right] \middle|\mathscr{F}_{0,\alpha,r}\right) \\&\le \sum_{{\mathbb{E} I<2j\le m_{\alpha,r}}}\mathbb{P}(I=j)\mathbb{E}\!\left(\mathbb{E}\!\left[\sup_{A\in \mathscr{B}(\mathbb{R})}\left(\textbf{1}_{{\Sigma_{3,j}}\in A}-\textbf{1}_{{\Sigma_{3,j}}\in A-h_{\alpha,r}\left(\Xi_{N_{\alpha, r}^{(2)}}\right)}\middle| \sigma\!\left(\Xi_{N_{\alpha,r}^{(2)}}\right)\right)\right]\middle|\mathscr{F}_{0,\alpha,r}\right)\nonumber \\&\quad +\mathbb{P}(I\le (\mathbb{E} I)/2)\nonumber\end{align}
\begin{align} & \quad d_{TV}\!\left(\bar{W}^{\prime}_{\alpha,r},\bar{W}^{\prime}_{\alpha,r}+h_{\alpha,r}\left(\Xi_{N_{\alpha, r}^{(2)}}\right)\middle|\mathscr{F}_{0,\alpha,r}\right)\nonumber \\&\le \mathbb{E}\!\left(\sup_{A\in \mathscr{B}(\mathbb{R})}\left[\mathbb{E}\!\left(\textbf{1}_{\bar{W}_{\alpha,r}^0\in A}-\textbf{1}_{\bar{W}_{\alpha,r}^0\in A-h_{\alpha,r}\left(\Xi_{N_{\alpha, r}^{(2)}}\right)}\middle|\mathscr{F}^{\prime}_{2,\alpha,r}\right)\right]\middle|\mathscr{F}_{0,\alpha,r}\right)\nonumber \\&\le \mathbb{E}\!\left(\mathbb{E}\!\left[\sup_{A\in \mathscr{B}(\mathbb{R})}\left(\textbf{1}_{{\Sigma_{3,I}}\in A}-\textbf{1}_{{\Sigma_{3,I}}\in A-h_{\alpha,r}\left(\Xi_{N_{\alpha, r}^{(2)}}\right)}\middle|I,\sigma\!\left(\Xi_{N_{\alpha,r}^{(2)}}\right)\right)\right] \middle|\mathscr{F}_{0,\alpha,r}\right) \\&\le \sum_{{\mathbb{E} I<2j\le m_{\alpha,r}}}\mathbb{P}(I=j)\mathbb{E}\!\left(\mathbb{E}\!\left[\sup_{A\in \mathscr{B}(\mathbb{R})}\left(\textbf{1}_{{\Sigma_{3,j}}\in A}-\textbf{1}_{{\Sigma_{3,j}}\in A-h_{\alpha,r}\left(\Xi_{N_{\alpha, r}^{(2)}}\right)}\middle| \sigma\!\left(\Xi_{N_{\alpha,r}^{(2)}}\right)\right)\right]\middle|\mathscr{F}_{0,\alpha,r}\right)\nonumber \\&\quad +\mathbb{P}(I\le (\mathbb{E} I)/2)\nonumber\end{align}
 \begin{align}\le& \mathop{{}\textrm{O}}\mathopen{}\left(\alpha^{-1}r^d\right)+\mathop{{}\textrm{O}}\mathopen{}\left(\alpha^{-\frac{1}{2}}r^{\frac{d}{2}}\right)\mathbb{E}\!\left(\left|h_{\alpha,r}\left(\Xi_{N_{\alpha, r}^{(2)}}\right)\right|\middle| \mathscr{F}_{0,\alpha,r}\right)\qquad\qquad\qquad\qquad\qquad\qquad \\=& \mathbb{E}\!\left(\left|h_{\alpha,r}\left(\Xi_{N_{\alpha, r}^{(2)}}\right)\right|\vee 1\middle| \mathscr{F}_{0,\alpha,r}\right)\mathop{{}\textrm{O}}\mathopen{}\left(\alpha^{-\frac{1}{2}}r^{\frac{d}{2}}\right),\qquad\qquad\qquad\qquad\qquad\nonumber\end{align}
\begin{align}\le& \mathop{{}\textrm{O}}\mathopen{}\left(\alpha^{-1}r^d\right)+\mathop{{}\textrm{O}}\mathopen{}\left(\alpha^{-\frac{1}{2}}r^{\frac{d}{2}}\right)\mathbb{E}\!\left(\left|h_{\alpha,r}\left(\Xi_{N_{\alpha, r}^{(2)}}\right)\right|\middle| \mathscr{F}_{0,\alpha,r}\right)\qquad\qquad\qquad\qquad\qquad\qquad \\=& \mathbb{E}\!\left(\left|h_{\alpha,r}\left(\Xi_{N_{\alpha, r}^{(2)}}\right)\right|\vee 1\middle| \mathscr{F}_{0,\alpha,r}\right)\mathop{{}\textrm{O}}\mathopen{}\left(\alpha^{-\frac{1}{2}}r^{\frac{d}{2}}\right),\qquad\qquad\qquad\qquad\qquad\nonumber\end{align}
where (5.22) follows from the fact that
 \begin{equation*}\sup_{A\in \mathscr{B}(\mathbb{R})}\left[\textbf{1}_{{\Sigma_{3,I}}\in A}-\textbf{1}_{{\Sigma_{3,I}}\in A-h_{\alpha,r}\left(\Xi_{N_{\alpha, r}^{(2)}}\right)}\right]\end{equation*}
\begin{equation*}\sup_{A\in \mathscr{B}(\mathbb{R})}\left[\textbf{1}_{{\Sigma_{3,I}}\in A}-\textbf{1}_{{\Sigma_{3,I}}\in A-h_{\alpha,r}\left(\Xi_{N_{\alpha, r}^{(2)}}\right)}\right]\end{equation*}
is a function of I and
![]() $\Xi_{N_{\alpha, r}^{(2)}}$
, the first term of (5.23) is from Chebyshev’s inequality, and the second term is due to Lemma 4.1. This completes the proof for the statement of
$\Xi_{N_{\alpha, r}^{(2)}}$
, the first term of (5.23) is from Chebyshev’s inequality, and the second term is due to Lemma 4.1. This completes the proof for the statement of
![]() $\bar{W}_{\alpha,r}$
.
$\bar{W}_{\alpha,r}$
.
The claim (4.8) can be proved by replacing
![]() $\bar{W}_{\alpha,r}$
with
$\bar{W}_{\alpha,r}$
with
![]() $W_{\alpha,r}$
,
$W_{\alpha,r}$
,
![]() $\bar{W}^{\prime}_{\alpha,r}$
with
$\bar{W}^{\prime}_{\alpha,r}$
with
![]() $W^{\prime}_{\alpha,r}$
, and
$W^{\prime}_{\alpha,r}$
, and
![]() $\bar{W}^0_{\alpha,r}$
with
$\bar{W}^0_{\alpha,r}$
with
![]() $W^0_{\alpha,r}$
.
$W^0_{\alpha,r}$
.
The moments of
![]() $W_{\alpha,r}$
and
$W_{\alpha,r}$
and
![]() $W_\alpha$
(resp.
$W_\alpha$
(resp.
![]() $\bar{W}_{\alpha,r}$
and
$\bar{W}_{\alpha,r}$
and
![]() $\bar{W}_\alpha$
) are established in the following lemmas using the ideas in [Reference Xia and Yukich51, Section 4]. Let
$\bar{W}_\alpha$
) are established in the following lemmas using the ideas in [Reference Xia and Yukich51, Section 4]. Let
![]() $\|X\|_p\,:\!=\,\mathbb{E}\!\left(|X|^p\right)^{\frac{1}{p}}$
be the
$\|X\|_p\,:\!=\,\mathbb{E}\!\left(|X|^p\right)^{\frac{1}{p}}$
be the
![]() $L_p$
norm of X, provided it is finite.
$L_p$
norm of X, provided it is finite.
Lemma 5.7.
-
(a) (Unrestricted case.) If the score function
 $\eta$
satisfies the k′th moment condition 2.3 with
$\eta$
satisfies the k′th moment condition 2.3 with
 $k^{\prime}>k\ge 1$
, then
$k^{\prime}>k\ge 1$
, then
 $\max_{0< l\le k}\left\{\|W_{\alpha}\|_l,\|W_{\alpha,r}\|_l\right\}\le C\alpha.$
$\max_{0< l\le k}\left\{\|W_{\alpha}\|_l,\|W_{\alpha,r}\|_l\right\}\le C\alpha.$
-
(b) (Restricted case.) If the score function
 $\eta$
satisfies the k′th moment condition (2.4) with
$\eta$
satisfies the k′th moment condition (2.4) with
 $k^{\prime}>k\ge 1$
, then
$k^{\prime}>k\ge 1$
, then
 $\max_{0< l\le k}\left\{\|\bar{W}_{\alpha}\|_l,\|\bar{W}_{\alpha,r}\|_l\right\}\le C\alpha.$
$\max_{0< l\le k}\left\{\|\bar{W}_{\alpha}\|_l,\|\bar{W}_{\alpha,r}\|_l\right\}\le C\alpha.$
Proof. The proof is adapted from that of [Reference Xia and Yukich51, Lemma 4.1]. We use the same notation as in the proof of Lemma 4.4, and start with the restricted case. To this end, it suffices to show
![]() $\|\bar{W}_{\alpha}\|_k{\vee \|W_{\alpha,r}\|_k}\le C\alpha$
, and the claim follows from Hölder’s inequality. Let
$\|\bar{W}_{\alpha}\|_k{\vee \|W_{\alpha,r}\|_k}\le C\alpha$
, and the claim follows from Hölder’s inequality. Let
![]() $N_\alpha\,:\!=\,\left|\bar\Xi_{\Gamma_{\alpha}}\right|$
; then
$N_\alpha\,:\!=\,\left|\bar\Xi_{\Gamma_{\alpha}}\right|$
; then
![]() $N_\alpha$
follows the Poisson distribution with parameter
$N_\alpha$
follows the Poisson distribution with parameter
![]() $\alpha \lambda$
. Using Minkowski’s inequality, we obtain
$\alpha \lambda$
. Using Minkowski’s inequality, we obtain
 \begin{align} \|\bar{W}_{\alpha}\|_k&\le\left\|\sum_{x\in \bar{\Xi}_{\Gamma_\alpha}}\left|g_\alpha\!\left(x,\Xi\right)\right|\right\|_k\nonumber \\=&\left\|\sum_{x\in \bar{\Xi}_{\Gamma_\alpha}}\left|g_\alpha\!\left(x,\Xi\right)\right|\left(\textbf{1}_{N_\alpha\le \alpha\lambda}+\sum_{j=0}^\infty\textbf{1}_{\alpha\lambda 2^{j}<N_\alpha\le \alpha\lambda 2^{j+1}}\right)\right\|_k\nonumber \\\le& \left\|\sum_{x\in \bar{\Xi}_{\Gamma_\alpha}}\left|g_\alpha\!\left(x,\Xi\right)\right|\textbf{1}_{N_\alpha\le \alpha\lambda}\right\|_k+\sum_{j=0}^\infty \left\|\sum_{x\in \bar{\Xi}_{\Gamma_\alpha}}\left|g_\alpha\!\left(x,\Xi\right)\right|\textbf{1}_{\alpha\lambda 2^{j}<N_\alpha\le \alpha\lambda 2^{j+1}}\right\|_k.\end{align}
\begin{align} \|\bar{W}_{\alpha}\|_k&\le\left\|\sum_{x\in \bar{\Xi}_{\Gamma_\alpha}}\left|g_\alpha\!\left(x,\Xi\right)\right|\right\|_k\nonumber \\=&\left\|\sum_{x\in \bar{\Xi}_{\Gamma_\alpha}}\left|g_\alpha\!\left(x,\Xi\right)\right|\left(\textbf{1}_{N_\alpha\le \alpha\lambda}+\sum_{j=0}^\infty\textbf{1}_{\alpha\lambda 2^{j}<N_\alpha\le \alpha\lambda 2^{j+1}}\right)\right\|_k\nonumber \\\le& \left\|\sum_{x\in \bar{\Xi}_{\Gamma_\alpha}}\left|g_\alpha\!\left(x,\Xi\right)\right|\textbf{1}_{N_\alpha\le \alpha\lambda}\right\|_k+\sum_{j=0}^\infty \left\|\sum_{x\in \bar{\Xi}_{\Gamma_\alpha}}\left|g_\alpha\!\left(x,\Xi\right)\right|\textbf{1}_{\alpha\lambda 2^{j}<N_\alpha\le \alpha\lambda 2^{j+1}}\right\|_k.\end{align}
Let
![]() $s=\frac{k^{\prime}}{k}>1$
and let t be its conjugate, i.e.,
$s=\frac{k^{\prime}}{k}>1$
and let t be its conjugate, i.e.,
![]() $\frac{1}{s}+\frac{1}{t}=1$
. Using Hölder’s inequality and Minkowski’s inequality, for any
$\frac{1}{s}+\frac{1}{t}=1$
. Using Hölder’s inequality and Minkowski’s inequality, for any
![]() $j\in \mathbb{N}$
we have
$j\in \mathbb{N}$
we have
 \begin{align} &\left\|\sum_{x\in \bar{\Xi}_{\Gamma_\alpha}}\left|g_\alpha\!\left(x,\Xi\right)\right|\textbf{1}_{\alpha\lambda 2^{j}<N_\alpha\le \alpha\lambda 2^{j+1}}\right\|_k\nonumber \\=&\left\|\sum_{x\in \bar{\Xi}_{\Gamma_\alpha}}\left|g_\alpha\!\left(x,\Xi\right)\right|\textbf{1}_{N_\alpha\le \alpha\lambda 2^{j+1}}\textbf{1}_{\alpha\lambda 2^{j}<N_\alpha }\right\|_k\nonumber \\\le&\left\|\sum_{x\in \bar{\Xi}_{\Gamma_\alpha}}\left|g_\alpha\!\left(x,\Xi\right)\right|\textbf{1}_{N_\alpha\le \alpha\lambda 2^{j+1}}\right\|_{k^{\prime}}\left(\mathbb{P}\!\left(N_\alpha \gt \alpha\lambda 2^{j}\right)\right)^{\frac{1}{kt}}\nonumber \\ =& \left\|\sum_{x\in \bar{\Xi}_{\Gamma_\alpha}}\left|g_\alpha\!\left(x,\Xi\right)\right|\textbf{1}_{N_\alpha\le \alpha\lambda 2^{j+1}}\right\|_{k^{\prime}}\mathbb{P}\!\left(N_\alpha-\alpha\lambda\gt\alpha\lambda \!\left(2^{j}-1\right)\right)^{\frac{1}{kt}}.\end{align}
\begin{align} &\left\|\sum_{x\in \bar{\Xi}_{\Gamma_\alpha}}\left|g_\alpha\!\left(x,\Xi\right)\right|\textbf{1}_{\alpha\lambda 2^{j}<N_\alpha\le \alpha\lambda 2^{j+1}}\right\|_k\nonumber \\=&\left\|\sum_{x\in \bar{\Xi}_{\Gamma_\alpha}}\left|g_\alpha\!\left(x,\Xi\right)\right|\textbf{1}_{N_\alpha\le \alpha\lambda 2^{j+1}}\textbf{1}_{\alpha\lambda 2^{j}<N_\alpha }\right\|_k\nonumber \\\le&\left\|\sum_{x\in \bar{\Xi}_{\Gamma_\alpha}}\left|g_\alpha\!\left(x,\Xi\right)\right|\textbf{1}_{N_\alpha\le \alpha\lambda 2^{j+1}}\right\|_{k^{\prime}}\left(\mathbb{P}\!\left(N_\alpha \gt \alpha\lambda 2^{j}\right)\right)^{\frac{1}{kt}}\nonumber \\ =& \left\|\sum_{x\in \bar{\Xi}_{\Gamma_\alpha}}\left|g_\alpha\!\left(x,\Xi\right)\right|\textbf{1}_{N_\alpha\le \alpha\lambda 2^{j+1}}\right\|_{k^{\prime}}\mathbb{P}\!\left(N_\alpha-\alpha\lambda\gt\alpha\lambda \!\left(2^{j}-1\right)\right)^{\frac{1}{kt}}.\end{align}
For the term
![]() $\|\cdot\|_{k^{\prime}}$
in (5.25), we have
$\|\cdot\|_{k^{\prime}}$
in (5.25), we have
 \begin{align} &\left\|\sum_{x\in \bar{\Xi}_{\Gamma_\alpha}}\left|g_\alpha\!\left(x,\Xi\right)\right|\textbf{1}_{N_\alpha\le n}\right\|_{k^{\prime}}\nonumber \\=&\left\{\mathbb{E}\!\left[\left(\sum_{j=1}^n\sum_{x\in \bar{\Xi}_{\Gamma_\alpha}}\left|g_\alpha\!\left(x,\Xi\right)\right|\textbf{1}_{N_\alpha=j}\right)^{k^{\prime}}\right]\right\}^{\frac{1}{k^{\prime}}}\nonumber \\=& \left\{\sum_{j=1}^n\mathbb{E}\!\left[\left(\sum_{x\in \bar{\Xi}_{\Gamma_\alpha}}\left|g_\alpha\!\left(x,\Xi\right)\right|\textbf{1}_{N_\alpha=j}\right)^{k^{\prime}}\right]\right\}^{\frac{1}{k^{\prime}}},\end{align}
\begin{align} &\left\|\sum_{x\in \bar{\Xi}_{\Gamma_\alpha}}\left|g_\alpha\!\left(x,\Xi\right)\right|\textbf{1}_{N_\alpha\le n}\right\|_{k^{\prime}}\nonumber \\=&\left\{\mathbb{E}\!\left[\left(\sum_{j=1}^n\sum_{x\in \bar{\Xi}_{\Gamma_\alpha}}\left|g_\alpha\!\left(x,\Xi\right)\right|\textbf{1}_{N_\alpha=j}\right)^{k^{\prime}}\right]\right\}^{\frac{1}{k^{\prime}}}\nonumber \\=& \left\{\sum_{j=1}^n\mathbb{E}\!\left[\left(\sum_{x\in \bar{\Xi}_{\Gamma_\alpha}}\left|g_\alpha\!\left(x,\Xi\right)\right|\textbf{1}_{N_\alpha=j}\right)^{k^{\prime}}\right]\right\}^{\frac{1}{k^{\prime}}},\end{align}
where the first equality holds because
and the last equality follows from the fact that
![]() $\{N_\alpha=j\}$
,
$\{N_\alpha=j\}$
,
![]() $1\le j\le n$
, are disjoint events. On
$1\le j\le n$
, are disjoint events. On
![]() $\{N_\alpha=j\}$
for some fixed
$\{N_\alpha=j\}$
for some fixed
![]() $j\in \mathbb{N}$
, if we write j points in
$j\in \mathbb{N}$
, if we write j points in
![]() $\Xi\cap \Gamma_\alpha$
as
$\Xi\cap \Gamma_\alpha$
as
![]() $\{(x_1,m_1),\dots,(x_j,m_j)\}$
, and let
$\{(x_1,m_1),\dots,(x_j,m_j)\}$
, and let
![]() $\{\left(U_{\alpha,i},M_i\right)\}_{i\in \mathbb{N}}$
be a sequence of i.i.d. random elements that have distribution
$\{\left(U_{\alpha,i},M_i\right)\}_{i\in \mathbb{N}}$
be a sequence of i.i.d. random elements that have distribution
![]() $U\!\left(\Gamma_\alpha\right)\times \mathscr{L}_T$
and are independent of
$U\!\left(\Gamma_\alpha\right)\times \mathscr{L}_T$
and are independent of
![]() $\Xi$
, where
$\Xi$
, where
![]() $U\!\left(\Gamma_\alpha\right)$
is the uniform distribution on
$U\!\left(\Gamma_\alpha\right)$
is the uniform distribution on
![]() $\Gamma_\alpha$
, then
$\Gamma_\alpha$
, then
 \begin{align} &\quad \mathbb{E}\!\left[\left(\sum_{x\in \bar{\Xi}_{\Gamma_\alpha}}\left|g_\alpha\!\left(x,\Xi\right)\right|\textbf{1}_{N_\alpha=j}\right)^{k^{\prime}}\right]\nonumber \\ &\le \left\{\sum_{i=1}^j\mathbb{E}\!\left[\left|g_\alpha\!\left((x_i,m_i),\Xi\right)\right|^{k^{\prime}}\textbf{1}_{N_\alpha=j}\right]^{\frac{1}{k^{\prime}}}\right\}^{k^{\prime}}\nonumber \\ &= j^{k^{\prime}}\mathbb{E}\!\left[\left|g_\alpha\!\left(\left(U_{\alpha,i},M_i\right), \left(\sum_{i=1}^j \delta_{\left(U_{\alpha,i},M_i\right)}\right)\right)\right|^{k^{\prime}}\textbf{1}_{N_\alpha=j}\right],\end{align}
\begin{align} &\quad \mathbb{E}\!\left[\left(\sum_{x\in \bar{\Xi}_{\Gamma_\alpha}}\left|g_\alpha\!\left(x,\Xi\right)\right|\textbf{1}_{N_\alpha=j}\right)^{k^{\prime}}\right]\nonumber \\ &\le \left\{\sum_{i=1}^j\mathbb{E}\!\left[\left|g_\alpha\!\left((x_i,m_i),\Xi\right)\right|^{k^{\prime}}\textbf{1}_{N_\alpha=j}\right]^{\frac{1}{k^{\prime}}}\right\}^{k^{\prime}}\nonumber \\ &= j^{k^{\prime}}\mathbb{E}\!\left[\left|g_\alpha\!\left(\left(U_{\alpha,i},M_i\right), \left(\sum_{i=1}^j \delta_{\left(U_{\alpha,i},M_i\right)}\right)\right)\right|^{k^{\prime}}\textbf{1}_{N_\alpha=j}\right],\end{align}
where the inequality follows from Minkowski’s inequality, and the equality follows from the fact that when
![]() $\left|\bar{\Xi}\cap \Gamma_\alpha\right|$
is fixed, points in
$\left|\bar{\Xi}\cap \Gamma_\alpha\right|$
is fixed, points in
![]() $\bar{\Xi}\cap \Gamma_\alpha$
are independent and follow the uniform distribution on
$\bar{\Xi}\cap \Gamma_\alpha$
are independent and follow the uniform distribution on
![]() $\Gamma_\alpha$
. Combining (5.26) and (5.27), we have
$\Gamma_\alpha$
. Combining (5.26) and (5.27), we have
 \begin{align} & \quad \left\|\sum_{x\in \bar{\Xi}_{\Gamma_\alpha}}\left|g_\alpha\!\left(x,\Xi\right)\right|\textbf{1}_{N_\alpha\le n}\right\|_{k^{\prime}}\nonumber\nonumber \\ & \le \left\{\sum_{j=1}^nj^{k^{\prime}}\mathbb{E}\!\left[\left|g_\alpha\!\left(\left(U_{\alpha,1},M_1\right), \left(\sum_{i=1}^j \delta_{\left(U_{\alpha,i},M_i\right)}\right)\right)\right|^{k^{\prime}}\textbf{1}_{N_\alpha=j}\right]\right\}^{\frac{1}{k^{\prime}}}\nonumber \\ & =\left\{\sum_{j=1}^n\lambda \alpha j^{k^{\prime}-1}\mathbb{E}\!\left[\left|g_\alpha\!\left(\left(U_{\alpha,1},M_1\right), \left(\sum_{i=1}^j \delta_{\left(U_{\alpha,i},M_i\right)}\right)\right)\right|^{k^{\prime}}\textbf{1}_{N_\alpha=j-1}\right]\right\}^{\frac{1}{k^{\prime}}}\nonumber \\ & \le (\lambda\alpha)^{\frac{1}{k^{\prime}}}n^{\frac{k^{\prime}-1}{k^{\prime}}}\left\{\mathbb{E}\!\left[\sum_{j=0}^{n-1}\left|g_\alpha\!\left(\left(U_{\alpha,1},M_1\right), \left(\sum_{i=1}^{j+1} \delta_{\left(U_{\alpha,i},M_i\right)}\right)\right)\right|^{k^{\prime}}\textbf{1}_{N_\alpha=j}\right]\right\}^{\frac{1}{k^{\prime}}}\nonumber \\ & \le (\lambda\alpha)^{\frac{1}{k^{\prime}}}n^{\frac{k^{\prime}-1}{k^{\prime}}}\left\{\mathbb{E}\!\left[\sum_{j=0}^{\infty}\left|g_\alpha\!\left(\left(U_{\alpha,1},M_1\right), \left(\sum_{i=1}^{j+1} \delta_{\left(U_{\alpha,i},M_i\right)}\right)\right)\right|^{k^{\prime}}\textbf{1}_{N_\alpha=j}\right]\right\}^{\frac{1}{k^{\prime}}}\nonumber \\ & = (\lambda\alpha)^{\frac{1}{k^{\prime}}}n^{\frac{k^{\prime}-1}{k^{\prime}}}\left\{\int_{\Gamma_\alpha}\mathbb{E}\!\left[\left|g_\alpha\!\left((x,M),{\Xi_{\Gamma_\alpha}+\delta_{(x,M)}}\right)\right|^{k^{\prime}}\frac{1}{\alpha}dx\right]\right\}^{\frac{1}{k^{\prime}}}\nonumber \\&\le (\lambda\alpha)^{\frac{1}{k^{\prime}}}n^{\frac{k^{\prime}-1}{k^{\prime}}} C_0^{\frac{1}{k^{\prime}}},\end{align}
\begin{align} & \quad \left\|\sum_{x\in \bar{\Xi}_{\Gamma_\alpha}}\left|g_\alpha\!\left(x,\Xi\right)\right|\textbf{1}_{N_\alpha\le n}\right\|_{k^{\prime}}\nonumber\nonumber \\ & \le \left\{\sum_{j=1}^nj^{k^{\prime}}\mathbb{E}\!\left[\left|g_\alpha\!\left(\left(U_{\alpha,1},M_1\right), \left(\sum_{i=1}^j \delta_{\left(U_{\alpha,i},M_i\right)}\right)\right)\right|^{k^{\prime}}\textbf{1}_{N_\alpha=j}\right]\right\}^{\frac{1}{k^{\prime}}}\nonumber \\ & =\left\{\sum_{j=1}^n\lambda \alpha j^{k^{\prime}-1}\mathbb{E}\!\left[\left|g_\alpha\!\left(\left(U_{\alpha,1},M_1\right), \left(\sum_{i=1}^j \delta_{\left(U_{\alpha,i},M_i\right)}\right)\right)\right|^{k^{\prime}}\textbf{1}_{N_\alpha=j-1}\right]\right\}^{\frac{1}{k^{\prime}}}\nonumber \\ & \le (\lambda\alpha)^{\frac{1}{k^{\prime}}}n^{\frac{k^{\prime}-1}{k^{\prime}}}\left\{\mathbb{E}\!\left[\sum_{j=0}^{n-1}\left|g_\alpha\!\left(\left(U_{\alpha,1},M_1\right), \left(\sum_{i=1}^{j+1} \delta_{\left(U_{\alpha,i},M_i\right)}\right)\right)\right|^{k^{\prime}}\textbf{1}_{N_\alpha=j}\right]\right\}^{\frac{1}{k^{\prime}}}\nonumber \\ & \le (\lambda\alpha)^{\frac{1}{k^{\prime}}}n^{\frac{k^{\prime}-1}{k^{\prime}}}\left\{\mathbb{E}\!\left[\sum_{j=0}^{\infty}\left|g_\alpha\!\left(\left(U_{\alpha,1},M_1\right), \left(\sum_{i=1}^{j+1} \delta_{\left(U_{\alpha,i},M_i\right)}\right)\right)\right|^{k^{\prime}}\textbf{1}_{N_\alpha=j}\right]\right\}^{\frac{1}{k^{\prime}}}\nonumber \\ & = (\lambda\alpha)^{\frac{1}{k^{\prime}}}n^{\frac{k^{\prime}-1}{k^{\prime}}}\left\{\int_{\Gamma_\alpha}\mathbb{E}\!\left[\left|g_\alpha\!\left((x,M),{\Xi_{\Gamma_\alpha}+\delta_{(x,M)}}\right)\right|^{k^{\prime}}\frac{1}{\alpha}dx\right]\right\}^{\frac{1}{k^{\prime}}}\nonumber \\&\le (\lambda\alpha)^{\frac{1}{k^{\prime}}}n^{\frac{k^{\prime}-1}{k^{\prime}}} C_0^{\frac{1}{k^{\prime}}},\end{align}
where the first equality follows from the fact that
![]() $N_\alpha$
is independent of
$N_\alpha$
is independent of
![]() $\{\left(U_{\alpha,i},M_i\right)\}_{i\in \mathbb{N}}$
,
$\{\left(U_{\alpha,i},M_i\right)\}_{i\in \mathbb{N}}$
,
![]() $\mathbb{P}(N_\alpha=j)=\frac{\lambda \alpha}{j}\mathbb{P}(N_\alpha=j-1)$
, and the last equality follows from the construction of the marked Poisson point process.
$\mathbb{P}(N_\alpha=j)=\frac{\lambda \alpha}{j}\mathbb{P}(N_\alpha=j-1)$
, and the last equality follows from the construction of the marked Poisson point process.
Combining (5.25) and (5.28), we have
 \begin{align} \left\|\sum_{x\in \bar{\Xi}_{\Gamma_\alpha}}\big|g_\alpha\!\left(x,\Xi\big)\right|\textbf{1}_{\alpha\lambda 2^{j}<N_\alpha\le \alpha\lambda 2^{j+1}}\right\|_k\le \alpha\lambda 2^{\frac{(k^{\prime}-1)(j+1)}{k^{\prime}}}C_0^{\frac{1}{k^{\prime}}} \mathbb{P}\!\left(N_\alpha-\alpha\lambda>\alpha\lambda \!\left(2^{j}-1\right)\right)^{\frac{1}{kt}}.\end{align}
\begin{align} \left\|\sum_{x\in \bar{\Xi}_{\Gamma_\alpha}}\big|g_\alpha\!\left(x,\Xi\big)\right|\textbf{1}_{\alpha\lambda 2^{j}<N_\alpha\le \alpha\lambda 2^{j+1}}\right\|_k\le \alpha\lambda 2^{\frac{(k^{\prime}-1)(j+1)}{k^{\prime}}}C_0^{\frac{1}{k^{\prime}}} \mathbb{P}\!\left(N_\alpha-\alpha\lambda>\alpha\lambda \!\left(2^{j}-1\right)\right)^{\frac{1}{kt}}.\end{align}
Using (5.28) and Hölder’s inequality, we have
 \begin{align} &\left\|\sum_{x\in \bar{\Xi}_{\Gamma_\alpha}}\big|g_\alpha\!\big(x,\Xi\big)\big|\textbf{1}_{N_\alpha\le \alpha\lambda}\right\|_k\le\left\|\sum_{x\in \bar{\Xi}_{\Gamma_\alpha}}\left|g_\alpha\!\left(x,\Xi\right)\right|\textbf{1}_{N_\alpha\le \alpha\lambda}\right\|_{k^{\prime}}\le \alpha\lambda C_0^{\frac{1}{k^{\prime}}}.\end{align}
\begin{align} &\left\|\sum_{x\in \bar{\Xi}_{\Gamma_\alpha}}\big|g_\alpha\!\big(x,\Xi\big)\big|\textbf{1}_{N_\alpha\le \alpha\lambda}\right\|_k\le\left\|\sum_{x\in \bar{\Xi}_{\Gamma_\alpha}}\left|g_\alpha\!\left(x,\Xi\right)\right|\textbf{1}_{N_\alpha\le \alpha\lambda}\right\|_{k^{\prime}}\le \alpha\lambda C_0^{\frac{1}{k^{\prime}}}.\end{align}
Combining (5.29) and (5.30), together with the fact that
![]() $\mathbb{P}\!\left(N_\alpha-\alpha\lambda>\alpha\lambda k\right)$
decreases exponentially fast with respect to k, we have from (5.24) that
$\mathbb{P}\!\left(N_\alpha-\alpha\lambda>\alpha\lambda k\right)$
decreases exponentially fast with respect to k, we have from (5.24) that
 \begin{equation*}\|\bar{W}_{\alpha}\|_k\le\left\|\sum_{x\in \bar{\Xi}_{\Gamma_\alpha}}\left|g_\alpha\!\left(x,\Xi\right)\right|\right\|_k\le C\alpha.\end{equation*}
\begin{equation*}\|\bar{W}_{\alpha}\|_k\le\left\|\sum_{x\in \bar{\Xi}_{\Gamma_\alpha}}\left|g_\alpha\!\left(x,\Xi\right)\right|\right\|_k\le C\alpha.\end{equation*}
The proof of (b) is completed by observing that, for arbitrary
![]() $r\in \mathbb{R}_+$
,
$r\in \mathbb{R}_+$
,
 \begin{equation*}\|\bar{W}_{\alpha,r}\|_k=\left\|\sum_{x\in \bar{\Xi}_{\Gamma_\alpha}}g_\alpha\!\left(x,\Xi\right)\textbf{1}_{R(x)\le r}\right\|_k\le\left\|\sum_{x\in \bar{\Xi}_{\Gamma_\alpha}}\left|g_\alpha\!\left(x,\Xi\right)\right|\right\|_k\le C\alpha.\end{equation*}
\begin{equation*}\|\bar{W}_{\alpha,r}\|_k=\left\|\sum_{x\in \bar{\Xi}_{\Gamma_\alpha}}g_\alpha\!\left(x,\Xi\right)\textbf{1}_{R(x)\le r}\right\|_k\le\left\|\sum_{x\in \bar{\Xi}_{\Gamma_\alpha}}\left|g_\alpha\!\left(x,\Xi\right)\right|\right\|_k\le C\alpha.\end{equation*}
The claim in (a) can be established by replacing
![]() $\bar{W}_{\alpha}$
with
$\bar{W}_{\alpha}$
with
![]() $W_\alpha$
,
$W_\alpha$
,
![]() $\bar{W}_{\alpha,r}$
with
$\bar{W}_{\alpha,r}$
with
![]() $W_{\alpha,r}$
,
$W_{\alpha,r}$
,
![]() $g_\alpha(x,\mathscr{X}\,)$
with
$g_\alpha(x,\mathscr{X}\,)$
with
![]() $g(\mathscr{X}^{\,x})$
, and
$g(\mathscr{X}^{\,x})$
, and
![]() $\sum_{i=1}^j \delta_{\left(U_{\alpha,i},M_i\right)}$
with
$\sum_{i=1}^j \delta_{\left(U_{\alpha,i},M_i\right)}$
with
![]() $\sum_{i=1}^j \delta_{\left(U_{\alpha,i},M_i\right)}+\Xi_{\Gamma_\alpha^c}$
.
$\sum_{i=1}^j \delta_{\left(U_{\alpha,i},M_i\right)}+\Xi_{\Gamma_\alpha^c}$
.
Remark 5.1. The proof of Lemma 5.7 does not depend on the shape of
![]() $\Gamma_\alpha$
, so the claims still hold if we replace
$\Gamma_\alpha$
, so the claims still hold if we replace
![]() $\Gamma_\alpha$
with a set
$\Gamma_\alpha$
with a set
![]() $A\in\mathscr{B}\big(\mathbb{R}^d\big)$
and
$A\in\mathscr{B}\big(\mathbb{R}^d\big)$
and
![]() $\alpha$
in the upper bound with the volume of A.
$\alpha$
in the upper bound with the volume of A.
With these preparations, we are ready to bound the differences
![]() $\left|{\textrm{Var}}\!\left(W_{\alpha}\right)-{\textrm{Var}}\big(W_{\alpha,r}\big)\right|$
and
$\left|{\textrm{Var}}\!\left(W_{\alpha}\right)-{\textrm{Var}}\big(W_{\alpha,r}\big)\right|$
and
![]() $\left|{\textrm{Var}}\!\left(\bar{W}_{\alpha}\right)-{\textrm{Var}}\!\left(\bar{W}_{\alpha,r}\right)\right|$
.
$\left|{\textrm{Var}}\!\left(\bar{W}_{\alpha}\right)-{\textrm{Var}}\!\left(\bar{W}_{\alpha,r}\right)\right|$
.
Lemma 5.8.
-
(a) (Unrestricted case.) Assume that the score function
 $\eta$
satisfies the k′th moment condition (2.3) for some
$\eta$
satisfies the k′th moment condition (2.3) for some
 $k^{\prime}>2$
. If
$k^{\prime}>2$
. If
 $\eta$
is exponentially stabilising as in Definition 2.1, then there exist positive constants
$\eta$
is exponentially stabilising as in Definition 2.1, then there exist positive constants
 $\alpha_0$
and C such that (5.31)for all
$\alpha_0$
and C such that (5.31)for all \begin{equation} \left|{\textrm{Var}}\!\left(W_{\alpha}\right)-{\textrm{Var}}\big(W_{\alpha,r}\big)\right|\le \frac{1}{\alpha} \end{equation}
\begin{equation} \left|{\textrm{Var}}\!\left(W_{\alpha}\right)-{\textrm{Var}}\big(W_{\alpha,r}\big)\right|\le \frac{1}{\alpha} \end{equation}
 $\alpha\ge\alpha_0$
and
$\alpha\ge\alpha_0$
and
 $r\ge C\ln (\alpha)$
. If
$r\ge C\ln (\alpha)$
. If
 $\eta$
is polynomially stabilising as in Definition 2.1 with parameter
$\eta$
is polynomially stabilising as in Definition 2.1 with parameter
 $\beta$
, then for any
$\beta$
, then for any
 $k\in (2,k^{\prime}) $
, there exists a positive constant C such that (5.32)for all
$k\in (2,k^{\prime}) $
, there exists a positive constant C such that (5.32)for all \begin{align} \left|{\textrm{Var}}\!\left(W_{\alpha}\right)-{\textrm{Var}}\big(W_{\alpha,r}\big)\right|&\le C\!\left(\alpha^{\frac{3k-2}{k}}r^{-\beta\frac{k-2}{k}}\right)\vee \left(\alpha^{\frac{3k-1}{k}}r^{-\beta\frac{k-1}{k}}\right) \end{align}
\begin{align} \left|{\textrm{Var}}\!\left(W_{\alpha}\right)-{\textrm{Var}}\big(W_{\alpha,r}\big)\right|&\le C\!\left(\alpha^{\frac{3k-2}{k}}r^{-\beta\frac{k-2}{k}}\right)\vee \left(\alpha^{\frac{3k-1}{k}}r^{-\beta\frac{k-1}{k}}\right) \end{align}
 $r\le \alpha^{\frac{1}{d}}$
.
$r\le \alpha^{\frac{1}{d}}$
.
-
(b) (Restricted case.) Assume that the score function
 $\eta$
satisfies the k′th moment condition (2.4) for some
$\eta$
satisfies the k′th moment condition (2.4) for some
 $k^{\prime}>2$
. If
$k^{\prime}>2$
. If
 $\eta$
is exponentially stabilising as in Definition 2.2, then there exist positive constants
$\eta$
is exponentially stabilising as in Definition 2.2, then there exist positive constants
 $\alpha_0$
and C such that (5.33)for all
$\alpha_0$
and C such that (5.33)for all \begin{equation} \left|{\textrm{Var}}\!\left(\bar{W}_{\alpha}\right)-{\textrm{Var}}\!\left(\bar{W}_{\alpha,r}\right)\right|\le \frac{1}{\alpha} \end{equation}
\begin{equation} \left|{\textrm{Var}}\!\left(\bar{W}_{\alpha}\right)-{\textrm{Var}}\!\left(\bar{W}_{\alpha,r}\right)\right|\le \frac{1}{\alpha} \end{equation}
 $\alpha\ge\alpha_0$
and
$\alpha\ge\alpha_0$
and
 $r\ge C\ln (\alpha)$
. If
$r\ge C\ln (\alpha)$
. If
 $\eta$
is polynomially stabilising as in Definition 2.2, with parameter
$\eta$
is polynomially stabilising as in Definition 2.2, with parameter
 $\beta$
, then for any
$\beta$
, then for any
 $k\in (2,k^{\prime}) $
, there exists a positive constant C such that (5.34)for all
$k\in (2,k^{\prime}) $
, there exists a positive constant C such that (5.34)for all \begin{align} \left|{\textrm{Var}}\!\left(\bar{W}_{\alpha}\right)-{\textrm{Var}}\!\left(\bar{W}_{\alpha,r}\right)\right|&\le C\!\left(\alpha^{\frac{3k-2}{k}}r^{-\beta\frac{k-2}{k}}\right)\vee \left(\alpha^{\frac{3k-1}{k}}r^{-\beta\frac{k-1}{k}}\right) \end{align}
\begin{align} \left|{\textrm{Var}}\!\left(\bar{W}_{\alpha}\right)-{\textrm{Var}}\!\left(\bar{W}_{\alpha,r}\right)\right|&\le C\!\left(\alpha^{\frac{3k-2}{k}}r^{-\beta\frac{k-2}{k}}\right)\vee \left(\alpha^{\frac{3k-1}{k}}r^{-\beta\frac{k-1}{k}}\right) \end{align}
 $r\le \alpha^{\frac{1}{d}}$
.
$r\le \alpha^{\frac{1}{d}}$
.
Proof. We start with (5.33). From Lemma 5.7(b), for fixed
![]() $k\in (2,k^{\prime}) $
, we have
$k\in (2,k^{\prime}) $
, we have
for some positive constant
![]() $C_0$
. Without loss of generality, we assume
$C_0$
. Without loss of generality, we assume
![]() $\alpha_0>1$
. Since
$\alpha_0>1$
. Since
assuming that the score function is exponentially stabilising as in Definition 2.2, we show that each of the terms in the right-hand side of (5.36) is bounded by
![]() $\frac{1}{2\alpha}$
for
$\frac{1}{2\alpha}$
for
![]() $\alpha$
and r sufficiently large. Clearly, the definition of
$\alpha$
and r sufficiently large. Clearly, the definition of
![]() $\bar{W}_{\alpha,r}$
implies that
$\bar{W}_{\alpha,r}$
implies that
![]() $\bar{W}_\alpha^2-\bar{W}_{\alpha,r}^2= 0$
if
$\bar{W}_\alpha^2-\bar{W}_{\alpha,r}^2= 0$
if
![]() $\bar{R}(x,\alpha)\le r$
for all
$\bar{R}(x,\alpha)\le r$
for all
![]() $x\in\bar\Xi_{\Gamma_\alpha}$
; hence it remains to tackle
$x\in\bar\Xi_{\Gamma_\alpha}$
; hence it remains to tackle
![]() $E_{r,\alpha}\,:\!=\,\{\bar{R}(x,\alpha)\le r\ \mbox{for all }x\in\bar\Xi_{\Gamma_\alpha}\}^c$
. As shown in the proof of Lemma 5.6,
$E_{r,\alpha}\,:\!=\,\{\bar{R}(x,\alpha)\le r\ \mbox{for all }x\in\bar\Xi_{\Gamma_\alpha}\}^c$
. As shown in the proof of Lemma 5.6,
![]() $\mathbb{P}\!\left(E_{r,\alpha}\right)\le\alpha C_1e^{-C_2r}$
, which, together with Hölder’s inequality, ensures that
$\mathbb{P}\!\left(E_{r,\alpha}\right)\le\alpha C_1e^{-C_2r}$
, which, together with Hölder’s inequality, ensures that
 \begin{align} \left|\mathbb{E}\!\left(\bar{W}_\alpha^2-\bar{W}_{\alpha,r}^2\right)\right|&=\left|\mathbb{E}\!\left[\left(\bar{W}_\alpha^2-\bar{W}_{\alpha,r}^2\right)\textbf{1}_{E_{r,\alpha}}\right]\right|\nonumber \\&\le \|\bar{W}_\alpha^2-\bar{W}_{\alpha,r}^2\|_{\frac{k}{2}}\|\textbf{1}_{E_{r,\alpha}}\|_{\frac{k}{k-2}}\nonumber \\&\le \left(\|\bar{W}_\alpha^2\|_{\frac{k}{2}}+\|\bar{W}_{\alpha,r}^2\|_{\frac{k}{2}}\right)\mathbb{P}(E_{r,\alpha})^{\frac{k-2}{k}}\nonumber \\&=\left(\|\bar{W}_\alpha\|_{k}^2+\|\bar{W}_{\alpha,r}\|_{k}^2\right)\mathbb{P}(E_{r,\alpha})^{\frac{k-2}{k}}\le 2\!\left(C_0\alpha\right)^2 \left(\alpha C_1e^{-C_2r}\right)^{\frac{k-2}{k}}.\end{align}
\begin{align} \left|\mathbb{E}\!\left(\bar{W}_\alpha^2-\bar{W}_{\alpha,r}^2\right)\right|&=\left|\mathbb{E}\!\left[\left(\bar{W}_\alpha^2-\bar{W}_{\alpha,r}^2\right)\textbf{1}_{E_{r,\alpha}}\right]\right|\nonumber \\&\le \|\bar{W}_\alpha^2-\bar{W}_{\alpha,r}^2\|_{\frac{k}{2}}\|\textbf{1}_{E_{r,\alpha}}\|_{\frac{k}{k-2}}\nonumber \\&\le \left(\|\bar{W}_\alpha^2\|_{\frac{k}{2}}+\|\bar{W}_{\alpha,r}^2\|_{\frac{k}{2}}\right)\mathbb{P}(E_{r,\alpha})^{\frac{k-2}{k}}\nonumber \\&=\left(\|\bar{W}_\alpha\|_{k}^2+\|\bar{W}_{\alpha,r}\|_{k}^2\right)\mathbb{P}(E_{r,\alpha})^{\frac{k-2}{k}}\le 2\!\left(C_0\alpha\right)^2 \left(\alpha C_1e^{-C_2r}\right)^{\frac{k-2}{k}}.\end{align}
For the remaining term of (5.36), we have
The bound (5.35) implies
![]() $\left|\mathbb{E}\bar{W}_\alpha+\mathbb{E}\bar{W}_{\alpha,r}\right|\le 2C_0\alpha $
. However, using Hölder’s inequality, Minkowski’s inequality, and (5.35) again, we have
$\left|\mathbb{E}\bar{W}_\alpha+\mathbb{E}\bar{W}_{\alpha,r}\right|\le 2C_0\alpha $
. However, using Hölder’s inequality, Minkowski’s inequality, and (5.35) again, we have
 \begin{align} \left|\mathbb{E}\bar{W}_\alpha-\mathbb{E}\bar{W}_{\alpha,r}\right|&=\left|\mathbb{E}\!\left[\left(\bar{W}_\alpha-\bar{W}_{\alpha,r}\right)\textbf{1}_{E_{r,\alpha}}\right]\right|\nonumber \\&\le \|\bar{W}_\alpha-\bar{W}_{\alpha,r}\|_k\|\textbf{1}_{E_{r,\alpha}}\|_{\frac{k}{k-1}}\nonumber \\&\le \left(\|\bar{W}_\alpha\|_{k}+\|\bar{W}_{\alpha,r}\|_{k}\right)\mathbb{P}(E_{r,\alpha})^{\frac{k-1}{k}}\nonumber \\&\le 2C_0\alpha \Big(\alpha C_1e^{-C_2r}\Big)^{\frac{k-1}{k}},\end{align}
\begin{align} \left|\mathbb{E}\bar{W}_\alpha-\mathbb{E}\bar{W}_{\alpha,r}\right|&=\left|\mathbb{E}\!\left[\left(\bar{W}_\alpha-\bar{W}_{\alpha,r}\right)\textbf{1}_{E_{r,\alpha}}\right]\right|\nonumber \\&\le \|\bar{W}_\alpha-\bar{W}_{\alpha,r}\|_k\|\textbf{1}_{E_{r,\alpha}}\|_{\frac{k}{k-1}}\nonumber \\&\le \left(\|\bar{W}_\alpha\|_{k}+\|\bar{W}_{\alpha,r}\|_{k}\right)\mathbb{P}(E_{r,\alpha})^{\frac{k-1}{k}}\nonumber \\&\le 2C_0\alpha \Big(\alpha C_1e^{-C_2r}\Big)^{\frac{k-1}{k}},\end{align}
giving
We set
![]() $r=C\ln\!(\alpha)$
in the upper bounds of (5.37) and (5.39), and find C such that both bounds are bounded by
$r=C\ln\!(\alpha)$
in the upper bounds of (5.37) and (5.39), and find C such that both bounds are bounded by
![]() $1/(2\alpha)$
, completing the proof of (5.33).
$1/(2\alpha)$
, completing the proof of (5.33).
The same proof can be adapted for (5.34). With (5.36) in mind, recalling the fact established in the proof of Lemma 5.6 that
![]() $\mathbb{P}(E_{r,\alpha})\le C_1\alpha r^{-\beta}$
, we replace the last inequalities of (5.37), (5.38), and (5.39) with the corresponding bound of
$\mathbb{P}(E_{r,\alpha})\le C_1\alpha r^{-\beta}$
, we replace the last inequalities of (5.37), (5.38), and (5.39) with the corresponding bound of
![]() $ \mathbb{P}(E_{r,\alpha})$
to obtain
$ \mathbb{P}(E_{r,\alpha})$
to obtain
The claim (5.34) follows from combining (5.40) and (5.42), extracting
![]() $\alpha$
and r, and then taking C as the sum of the remaining constants.
$\alpha$
and r, and then taking C as the sum of the remaining constants.
A line-by-line repetition of the above proof with
![]() $\bar{W}_\alpha$
and
$\bar{W}_\alpha$
and
![]() $\bar{W}_{\alpha,r}$
replaced by
$\bar{W}_{\alpha,r}$
replaced by
![]() $W_\alpha$
and
$W_\alpha$
and
![]() $W_{\alpha,r}$
gives (5.31) and (5.32) respectively.
$W_{\alpha,r}$
gives (5.31) and (5.32) respectively.
Next, we apply Lemma 5.2 and Lemma 5.3 to establish lower bounds for
![]() ${\textrm{Var}}\big(W_{\alpha,r}\big)$
and
${\textrm{Var}}\big(W_{\alpha,r}\big)$
and
![]() ${\textrm{Var}}\!\left(\bar{W}_{\alpha,r}\right)$
.
${\textrm{Var}}\!\left(\bar{W}_{\alpha,r}\right)$
.
Lemma 5.9.
-
(a) (Unrestricted case.) If the score function
 $\eta$
satisfies the polynomial stabilisation in Definition 2.1 with order
$\eta$
satisfies the polynomial stabilisation in Definition 2.1 with order
 $\beta>d+1$
and the non-singularity in Assumption 2.4, then
$\beta>d+1$
and the non-singularity in Assumption 2.4, then
 ${\textrm{Var}}\big(W_{\alpha,r}\big)\ge C\alpha r^{-d}$
for
${\textrm{Var}}\big(W_{\alpha,r}\big)\ge C\alpha r^{-d}$
for
 $R_0\le r\le \alpha^{1/d}/6$
, where
$R_0\le r\le \alpha^{1/d}/6$
, where
 $C,R_0>0$
are independent of
$C,R_0>0$
are independent of
 $\alpha$
.
$\alpha$
. -
(b) (Restricted case.) If the score function
 $\eta$
satisfies the polynomial stabilisation in Definition 2.2 with order
$\eta$
satisfies the polynomial stabilisation in Definition 2.2 with order
 $\beta>d+1$
and the non-singularity in Assumption 2.4, then
$\beta>d+1$
and the non-singularity in Assumption 2.4, then
 ${\textrm{Var}}\!\left(\bar{W}_{\alpha,r}\right)\ge C\alpha r^{-d}$
for
${\textrm{Var}}\!\left(\bar{W}_{\alpha,r}\right)\ge C\alpha r^{-d}$
for
 $R_0\le r\le \alpha^{1/d}/6$
, where
$R_0\le r\le \alpha^{1/d}/6$
, where
 $C,R_0>0$
are independent of
$C,R_0>0$
are independent of
 $\alpha$
.
$\alpha$
.
Proof. For (b), recalling the notation in the paragraph after (5.19), we obtain from the total variance formula that
 \begin{align} {\textrm{Var}}\!\left(\bar{W}_{\alpha,r}\right)& =\mathbb{E}\!\left({\textrm{Var}}\!\left(\bar{W}_{\alpha,r}\middle| \mathscr{F}_{2,\alpha,r} \right)\right)+{\textrm{Var}}\!\left(\mathbb{E}\!\left(\bar{W}_{\alpha,r}\middle| \mathscr{F}_{2,\alpha,r} \right)\right)\nonumber \\&\ge \mathbb{E}\!\left({\textrm{Var}}\!\left(\bar{W}_{\alpha,r}\middle| \mathscr{F}_{2,\alpha,r} \right)\right)\nonumber \\&=\sum_{i=1}^{m_{\alpha,r}}\mathbb{E}\!\left({\textrm{Var}}\!\left(\sum_{x\in \overline{\Xi}\cap B_i}{\bar{g}}(\Xi^{\Gamma_\alpha,x})\textbf{1}_{\bar{R}(x,\alpha)\le r }\middle|\Xi_{D_i}\right)\right)\nonumber \\&=m_{\alpha,r}\mathbb{E}\!\left({\textrm{Var}}\!\left(Y_r\middle|\Xi_{N_0^c}\right)\right),\end{align}
\begin{align} {\textrm{Var}}\!\left(\bar{W}_{\alpha,r}\right)& =\mathbb{E}\!\left({\textrm{Var}}\!\left(\bar{W}_{\alpha,r}\middle| \mathscr{F}_{2,\alpha,r} \right)\right)+{\textrm{Var}}\!\left(\mathbb{E}\!\left(\bar{W}_{\alpha,r}\middle| \mathscr{F}_{2,\alpha,r} \right)\right)\nonumber \\&\ge \mathbb{E}\!\left({\textrm{Var}}\!\left(\bar{W}_{\alpha,r}\middle| \mathscr{F}_{2,\alpha,r} \right)\right)\nonumber \\&=\sum_{i=1}^{m_{\alpha,r}}\mathbb{E}\!\left({\textrm{Var}}\!\left(\sum_{x\in \overline{\Xi}\cap B_i}{\bar{g}}(\Xi^{\Gamma_\alpha,x})\textbf{1}_{\bar{R}(x,\alpha)\le r }\middle|\Xi_{D_i}\right)\right)\nonumber \\&=m_{\alpha,r}\mathbb{E}\!\left({\textrm{Var}}\!\left(Y_r\middle|\Xi_{N_0^c}\right)\right),\end{align}
where
![]() $m_{\alpha,r}$
is the number of disjoint cubes with length
$m_{\alpha,r}$
is the number of disjoint cubes with length
![]() $4r+2r_1$
embedded into
$4r+2r_1$
embedded into
![]() $\Gamma_\alpha$
.
$\Gamma_\alpha$
.
Using (5.17), there exists an
![]() $R_0\ge r_1>0$
such that for all
$R_0\ge r_1>0$
such that for all
![]() $r>R_0$
,
$r>R_0$
,
 \begin{equation*}\mathscr{L}\!\left(Y_r\textbf{1}_{\Big(E^{\prime}_{R_0}\Big)^c}\middle|\Xi_{N_0^c}\right)=\mathscr{L}\!\left(\tilde{Y}\middle|\Xi_{N_0^c}\right)\ge \tilde{\xi} \mbox{ a.s.},\end{equation*}
\begin{equation*}\mathscr{L}\!\left(Y_r\textbf{1}_{\Big(E^{\prime}_{R_0}\Big)^c}\middle|\Xi_{N_0^c}\right)=\mathscr{L}\!\left(\tilde{Y}\middle|\Xi_{N_0^c}\right)\ge \tilde{\xi} \mbox{ a.s.},\end{equation*}
where
![]() $\tilde{\xi}$
is an absolutely continuous
$\tilde{\xi}$
is an absolutely continuous
![]() $\sigma\big(\Xi_{N_0^c}\big)$
-measurable random measure satisfying
$\sigma\big(\Xi_{N_0^c}\big)$
-measurable random measure satisfying
![]() $\mathbb{P}\!\left(\tilde{\xi}(\mathbb{R})>\frac{p}{2}\right)>2p$
. Hence, for
$\mathbb{P}\!\left(\tilde{\xi}(\mathbb{R})>\frac{p}{2}\right)>2p$
. Hence, for
![]() $r> R_0$
, we apply Lemma 5.3 with
$r> R_0$
, we apply Lemma 5.3 with
![]() $X\,:\!=\,Y_r$
,
$X\,:\!=\,Y_r$
,
![]() $A\,:\!=\,\Big(E^{\prime}_{R_0}\Big)^c$
, and use the fact that
$A\,:\!=\,\Big(E^{\prime}_{R_0}\Big)^c$
, and use the fact that
![]() $Y_r\textbf{1}_{\Big(E^{\prime}_{R_0}\Big)^c}=\tilde{Y}$
for all
$Y_r\textbf{1}_{\Big(E^{\prime}_{R_0}\Big)^c}=\tilde{Y}$
for all
![]() $r\ge R_0$
to obtain
$r\ge R_0$
to obtain
 \begin{equation} \mathbb{E}{\textrm{Var}}\!\left(Y_r\middle|\Xi_{N_0^c}\right)\ge \mathbb{E}{\textrm{Var}}\!\left({\tilde{Y}}+\frac{\mathbb{E}\!\left({\tilde{Y}}\middle|\Xi_{N_0^c}\right)}{\mathbb{P}\!\left(\Big(E^{\prime}_{R_0}\Big)^c\middle|\Xi_{N_0^c}\right)}\textbf{1}_{E^{\prime}_{R_0}}\middle|\Xi_{N_0^c}\right)\,=\!:\,b>0.\end{equation}
\begin{equation} \mathbb{E}{\textrm{Var}}\!\left(Y_r\middle|\Xi_{N_0^c}\right)\ge \mathbb{E}{\textrm{Var}}\!\left({\tilde{Y}}+\frac{\mathbb{E}\!\left({\tilde{Y}}\middle|\Xi_{N_0^c}\right)}{\mathbb{P}\!\left(\Big(E^{\prime}_{R_0}\Big)^c\middle|\Xi_{N_0^c}\right)}\textbf{1}_{E^{\prime}_{R_0}}\middle|\Xi_{N_0^c}\right)\,=\!:\,b>0.\end{equation}
The proof of the claim (b) is completed by combining (5.43) and (5.44), and observing that
![]() $R_0\le r\le \alpha^{1/d}/6$
ensures that
$R_0\le r\le \alpha^{1/d}/6$
ensures that
![]() $m_{\alpha,r}\ge 12^{-d}\alpha r^{-d}$
.
$m_{\alpha,r}\ge 12^{-d}\alpha r^{-d}$
.
The claim (a) can be proved by replacing
![]() $\bar{W}_{\alpha,r}$
with
$\bar{W}_{\alpha,r}$
with
![]() $W_{\alpha,r}$
and
$W_{\alpha,r}$
and
![]() $\bar{g}$
with g throughout the above argument.
$\bar{g}$
with g throughout the above argument.
Finally, we make use of [Reference Xia and Yukich51, Lemma 4.6], Lemma 5.8, and Lemma 5.9 to establish Lemma 4.5.
Proof of Lemma
4.5. To begin with, we combine (5.31), (5.33), and Lemma 5.9(a) to find an
![]() $r\,:\!=\,C_1\ln\!(\alpha)$
such that
$r\,:\!=\,C_1\ln\!(\alpha)$
such that
for positive constants
![]() $C_1,C_2$
. The inequalities (5.45) and (5.47) imply
$C_1,C_2$
. The inequalities (5.45) and (5.47) imply
![]() ${\textrm{Var}}\!\left(W_{\alpha}\right)\ge \mathop{{}\textrm{O}}\mathopen{}\left(\alpha \ln\!(\alpha)^{-d}\right)$
; hence the claim (a) follows from the dichotomy established in [Reference Xia and Yukich51, Lemma 4.6] saying either
${\textrm{Var}}\!\left(W_{\alpha}\right)\ge \mathop{{}\textrm{O}}\mathopen{}\left(\alpha \ln\!(\alpha)^{-d}\right)$
; hence the claim (a) follows from the dichotomy established in [Reference Xia and Yukich51, Lemma 4.6] saying either
![]() ${\textrm{Var}}\!\left(W_{\alpha}\right)=\Omega\!\left(\alpha\right)$
or
${\textrm{Var}}\!\left(W_{\alpha}\right)=\Omega\!\left(\alpha\right)$
or
![]() ${\textrm{Var}}\!\left(W_{\alpha}\right)=\mathop{{}\textrm{O}}\mathopen{}\left(\alpha^{\frac{d-1}{d}}\right)$
.
${\textrm{Var}}\!\left(W_{\alpha}\right)=\mathop{{}\textrm{O}}\mathopen{}\left(\alpha^{\frac{d-1}{d}}\right)$
.
For (b), it suffices to show that
![]() ${\textrm{Var}}\!\left(\bar{W}_{\alpha}\right)-{\textrm{Var}}\!\left(W_{\alpha}\right)=\mathop{{}\textrm{o}}\mathopen{}(\alpha)$
if we take
${\textrm{Var}}\!\left(\bar{W}_{\alpha}\right)-{\textrm{Var}}\!\left(W_{\alpha}\right)=\mathop{{}\textrm{o}}\mathopen{}(\alpha)$
if we take
![]() $\bar{\eta}$
as the score function in the unrestricted case. To this end, noting that (5.45) and (5.46), it remains to show that
$\bar{\eta}$
as the score function in the unrestricted case. To this end, noting that (5.45) and (5.46), it remains to show that
![]() ${\textrm{Var}}\big(W_{\alpha,r}\big)-{\textrm{Var}}\!\left(\bar{W}_{\alpha,r}\right)=\mathop{{}\textrm{o}}\mathopen{}(\alpha)$
. However, by the Cauchy–Schwarz inequality, we have
${\textrm{Var}}\big(W_{\alpha,r}\big)-{\textrm{Var}}\!\left(\bar{W}_{\alpha,r}\right)=\mathop{{}\textrm{o}}\mathopen{}(\alpha)$
. However, by the Cauchy–Schwarz inequality, we have
 \begin{align*} &\left|{\textrm{Var}}\big(W_{\alpha,r}\big)-{\textrm{Var}}\!\left(\bar{W}_{\alpha,r}\right)\right|\\ =&\left|{\textrm{Var}}\!\left(W_{\alpha,r}-\bar{W}_{\alpha,r}\right)-2\textrm{cov}\!\left(W_{\alpha,r}-\bar{W}_{\alpha,r},W_{\alpha,r}\right)\right| \\ \le& {\textrm{Var}}\!\left(W_{\alpha,r}-\bar{W}_{\alpha,r}\right)+2\sqrt{{\textrm{Var}}\!\left(W_{\alpha,r}-\bar{W}_{\alpha,r}\right){\textrm{Var}}\big(W_{\alpha,r}\big)},\end{align*}
\begin{align*} &\left|{\textrm{Var}}\big(W_{\alpha,r}\big)-{\textrm{Var}}\!\left(\bar{W}_{\alpha,r}\right)\right|\\ =&\left|{\textrm{Var}}\!\left(W_{\alpha,r}-\bar{W}_{\alpha,r}\right)-2\textrm{cov}\!\left(W_{\alpha,r}-\bar{W}_{\alpha,r},W_{\alpha,r}\right)\right| \\ \le& {\textrm{Var}}\!\left(W_{\alpha,r}-\bar{W}_{\alpha,r}\right)+2\sqrt{{\textrm{Var}}\!\left(W_{\alpha,r}-\bar{W}_{\alpha,r}\right){\textrm{Var}}\big(W_{\alpha,r}\big)},\end{align*}
and it follows from
![]() ${\textrm{Var}}\!\left(W_{\alpha}\right)=\Omega\!\left(\alpha\right)$
,
${\textrm{Var}}\!\left(W_{\alpha}\right)=\Omega\!\left(\alpha\right)$
,
![]() ${\textrm{Var}}(W_{\alpha,r})=\mathop{{}\textrm{O}}\mathopen{}(\alpha)$
, and (5.45) that
${\textrm{Var}}(W_{\alpha,r})=\mathop{{}\textrm{O}}\mathopen{}(\alpha)$
, and (5.45) that
![]() ${\textrm{Var}}\big(W_{\alpha,r}\big)=\Omega\!\left(\alpha\right)$
; hence the proof is reduced to showing
${\textrm{Var}}\big(W_{\alpha,r}\big)=\Omega\!\left(\alpha\right)$
; hence the proof is reduced to showing
![]() ${\textrm{Var}}\!\left(W_{\alpha,r}-\bar{W}_{\alpha,r}\right)=\mathop{{}\textrm{o}}\mathopen{}(\alpha)$
.
${\textrm{Var}}\!\left(W_{\alpha,r}-\bar{W}_{\alpha,r}\right)=\mathop{{}\textrm{o}}\mathopen{}(\alpha)$
.
Since
![]() ${g_\alpha\!\left(x,\Xi\right)}\textbf{1}_{\bar{R}(x,\alpha)<r}={\bar{g}}\left(\Xi^{x}\right)\textbf{1}_{R(x)<r}$
if
${g_\alpha\!\left(x,\Xi\right)}\textbf{1}_{\bar{R}(x,\alpha)<r}={\bar{g}}\left(\Xi^{x}\right)\textbf{1}_{R(x)<r}$
if
![]() $d(x, \partial\Gamma_{\alpha})>r$
, we have
$d(x, \partial\Gamma_{\alpha})>r$
, we have
![]() $W_{\alpha,r}-\bar{W}_{\alpha,r}=W_{1,\alpha,r}-W_{2,\alpha,r}$
where
$W_{\alpha,r}-\bar{W}_{\alpha,r}=W_{1,\alpha,r}-W_{2,\alpha,r}$
where
As the summands of
![]() $W_{1,\alpha,r}$
and
$W_{1,\alpha,r}$
and
![]() $W_{2,\alpha,r}$
are in the moat within distance r from the boundary of
$W_{2,\alpha,r}$
are in the moat within distance r from the boundary of
![]() $\Gamma_\alpha$
, both
$\Gamma_\alpha$
, both
![]() ${\textrm{Var}}\!\left(W_{1,\alpha,r^{\prime}_{\alpha}}\right)$
and
${\textrm{Var}}\!\left(W_{1,\alpha,r^{\prime}_{\alpha}}\right)$
and
![]() ${\textrm{Var}}\!\left(W_{2,\alpha,r^{\prime}_{\alpha}}\right)$
are of order
${\textrm{Var}}\!\left(W_{2,\alpha,r^{\prime}_{\alpha}}\right)$
are of order
![]() $\mathop{{}\textrm{o}}\mathopen{}(\alpha)$
, as detailed below. In fact, it follows from (5.4) that
$\mathop{{}\textrm{o}}\mathopen{}(\alpha)$
, as detailed below. In fact, it follows from (5.4) that
 \begin{align} &\quad \mathbb{E}\!\left( g_\alpha\!\left(x,\Xi\right)\textbf{1}_{\bar{R}(x,\alpha)<r}\bar{\Xi}(dx)\right)\nonumber\\ &=\mathbb{E}\!\left(g_\alpha\!\left(x,\Xi+\delta_{\big(x,{M_1}\big)}\right)\textbf{1}_{\bar{R}(x,{M_1},\alpha,\Xi+\delta_{\big(x,{M_1}\big)})<r}\right)\lambda dx\nonumber \\ &=\!:\,P_{x,\alpha,r} dx;\end{align}
\begin{align} &\quad \mathbb{E}\!\left( g_\alpha\!\left(x,\Xi\right)\textbf{1}_{\bar{R}(x,\alpha)<r}\bar{\Xi}(dx)\right)\nonumber\\ &=\mathbb{E}\!\left(g_\alpha\!\left(x,\Xi+\delta_{\big(x,{M_1}\big)}\right)\textbf{1}_{\bar{R}(x,{M_1},\alpha,\Xi+\delta_{\big(x,{M_1}\big)})<r}\right)\lambda dx\nonumber \\ &=\!:\,P_{x,\alpha,r} dx;\end{align}
if we set
then
![]() $\mathbb{E}\!\left(\bar{\Xi}_\alpha^\ast(dx)\bar{\Xi}_\alpha^\ast(dy)\right){=\mathbb{E}\!\left(\bar{\Xi}_\alpha^\ast(dx)\right)\mathbb{E}\!\left(\bar{\Xi}_\alpha^\ast(dy)\right)}=0$
if
$\mathbb{E}\!\left(\bar{\Xi}_\alpha^\ast(dx)\bar{\Xi}_\alpha^\ast(dy)\right){=\mathbb{E}\!\left(\bar{\Xi}_\alpha^\ast(dx)\right)\mathbb{E}\!\left(\bar{\Xi}_\alpha^\ast(dy)\right)}=0$
if
![]() $d(x,y)>2r$
. Therefore,
$d(x,y)>2r$
. Therefore,
 \begin{align} &{\textrm{Var}}\!\left({W_{2,\alpha,r}}\right)\nonumber\\ =&\int_{x,y\in B\!\left(\partial\Gamma_{\alpha},r\right)\cap\Gamma_\alpha}\mathbb{E}\!\left(\bar{\Xi}_\alpha^\ast(dx)\bar{\Xi}_\alpha^\ast(dy)\right)\nonumber \\ =&\int_{x,y\in B\!\left(\partial\Gamma_{\alpha},r\right)\cap\Gamma_\alpha,d(x,y)\le 2r}\mathbb{E}\!\left(\bar{\Xi}_\alpha^\ast(dx)\bar{\Xi}_\alpha^\ast(dy)\right)\nonumber\\ =&\int_{x,y\in B\!\left(\partial\Gamma_{\alpha},r\right)\cap\Gamma_\alpha,d(x,y)\le 2r} \left\{\mathbb{E}\!\left[{g_\alpha\!\left(x,\Xi\right)}\textbf{1}_{\bar{R}(x,\alpha)<r}{g_\alpha\!\left(y,\Xi\right)}\textbf{1}_{\bar{R}(y,\alpha)<r}\bar{\Xi}(dx)\bar{\Xi}(dy)\right]\right.\nonumber\\[5pt]& \qquad\qquad \left.-P_{x,\alpha,r}P_{y,\alpha,r} dxdy\right\}.\end{align}
\begin{align} &{\textrm{Var}}\!\left({W_{2,\alpha,r}}\right)\nonumber\\ =&\int_{x,y\in B\!\left(\partial\Gamma_{\alpha},r\right)\cap\Gamma_\alpha}\mathbb{E}\!\left(\bar{\Xi}_\alpha^\ast(dx)\bar{\Xi}_\alpha^\ast(dy)\right)\nonumber \\ =&\int_{x,y\in B\!\left(\partial\Gamma_{\alpha},r\right)\cap\Gamma_\alpha,d(x,y)\le 2r}\mathbb{E}\!\left(\bar{\Xi}_\alpha^\ast(dx)\bar{\Xi}_\alpha^\ast(dy)\right)\nonumber\\ =&\int_{x,y\in B\!\left(\partial\Gamma_{\alpha},r\right)\cap\Gamma_\alpha,d(x,y)\le 2r} \left\{\mathbb{E}\!\left[{g_\alpha\!\left(x,\Xi\right)}\textbf{1}_{\bar{R}(x,\alpha)<r}{g_\alpha\!\left(y,\Xi\right)}\textbf{1}_{\bar{R}(y,\alpha)<r}\bar{\Xi}(dx)\bar{\Xi}(dy)\right]\right.\nonumber\\[5pt]& \qquad\qquad \left.-P_{x,\alpha,r}P_{y,\alpha,r} dxdy\right\}.\end{align}
Recalling the second-order Palm distribution in (5.5), we can use the moment condition (2.4) together with Hölder’s inequality to obtain
where
![]() $C\ge 1$
. Combining these estimates with (5.50) gives
$C\ge 1$
. Combining these estimates with (5.50) gives
The proof of
![]() ${\textrm{Var}}\!\left({W_{1,\alpha,r}}\right)=\mathop{{}\textrm{o}}\mathopen{}(\alpha)$
is similar, except we replace (2.4) with (2.3). Consequently,
${\textrm{Var}}\!\left({W_{1,\alpha,r}}\right)=\mathop{{}\textrm{o}}\mathopen{}(\alpha)$
is similar, except we replace (2.4) with (2.3). Consequently,
and the statement follows.
As the lower bounds in Lemma 4.6 are very conservative, their proofs are less demanding, as demonstrated below.
Proof of Lemma 4.5. We start with (b). The bound (5.34) ensures that
for all
![]() $r\le \alpha^{\frac{1}{d}}$
and
$r\le \alpha^{\frac{1}{d}}$
and
![]() $k^{\prime}>k_0>k\ge3$
. On the other hand, Lemma 5.9(b) says
$k^{\prime}>k_0>k\ge3$
. On the other hand, Lemma 5.9(b) says
for
![]() $0<R_0\le r\le \alpha^{1/d}/6$
. Let
$0<R_0\le r\le \alpha^{1/d}/6$
. Let
![]() $r_\alpha\,:\!=\,\alpha^{\frac{2k-2}{k\beta-2\beta-dk}}$
. The assumption
$r_\alpha\,:\!=\,\alpha^{\frac{2k-2}{k\beta-2\beta-dk}}$
. The assumption
![]() $\beta>(3k-2)d/(k-2)$
ensures that
$\beta>(3k-2)d/(k-2)$
ensures that
![]() $r_\alpha<\alpha^{1/d}/6$
for large
$r_\alpha<\alpha^{1/d}/6$
for large
![]() $\alpha$
, and
$\alpha$
, and
![]() $k_0>k$
guarantees
$k_0>k$
guarantees
![]() $\left|{\textrm{Var}}\!\left(\bar{W}_{\alpha}\right)-{\textrm{Var}}\!\left(\bar{W}_{\alpha,r_\alpha}\right)\right|\ll {\textrm{Var}}\!\left(\bar{W}_{\alpha,r_\alpha}\right)$
for large
$\left|{\textrm{Var}}\!\left(\bar{W}_{\alpha}\right)-{\textrm{Var}}\!\left(\bar{W}_{\alpha,r_\alpha}\right)\right|\ll {\textrm{Var}}\!\left(\bar{W}_{\alpha,r_\alpha}\right)$
for large
![]() $\alpha$
. Hence
$\alpha$
. Hence
completing the proof.
For the proof of (a), we can proceed as in the proof of (b), replacing
![]() $\bar{W}_\alpha$
with
$\bar{W}_\alpha$
with
![]() $W_\alpha$
and
$W_\alpha$
and
![]() $\bar{W}_{\alpha,r}$
with
$\bar{W}_{\alpha,r}$
with
![]() $W_{\alpha,r}$
.
$W_{\alpha,r}$
.
The proof of Lemma 4.6 enables us to get slightly better bounds for
![]() ${\textrm{Var}}\big(W_{\alpha,r}\big)$
and
${\textrm{Var}}\big(W_{\alpha,r}\big)$
and
![]() ${\textrm{Var}}\!\left(\bar{W}_{\alpha,r}\right)$
.
${\textrm{Var}}\!\left(\bar{W}_{\alpha,r}\right)$
.
Lemma 5.10.
-
(a) (Unrestricted case.) If the score function
 $\eta$
satisfies the conditions of Lemma 4.6(a), then for
$\eta$
satisfies the conditions of Lemma 4.6(a), then for \begin{equation*}{\textrm{Var}}\big(W_{\alpha,r}\big)\ge C\big(\alpha r^{-d}\big)\vee\left(\alpha^{\frac{k\beta-2\beta-3dk+2d}{k\beta-2\beta-dk}}\right)\end{equation*}
\begin{equation*}{\textrm{Var}}\big(W_{\alpha,r}\big)\ge C\big(\alpha r^{-d}\big)\vee\left(\alpha^{\frac{k\beta-2\beta-3dk+2d}{k\beta-2\beta-dk}}\right)\end{equation*}
 $R_0\le r\le \alpha^{1/d}/6$
, where
$R_0\le r\le \alpha^{1/d}/6$
, where
 $C,R_0>0$
are independent of
$C,R_0>0$
are independent of
 $\alpha$
.
$\alpha$
.
-
(b) (Restricted case.) If the score function
 $\eta$
satisfies the conditions of Lemma 4.6(b), then for
$\eta$
satisfies the conditions of Lemma 4.6(b), then for \begin{equation*}{\textrm{Var}}\!\left(\bar{W}_{\alpha,r}\right)\ge C\big(\alpha r^{-d}\big)\vee\left(\alpha^{\frac{k\beta-2\beta-3dk+2d}{k\beta-2\beta-dk}}\right)\end{equation*}
\begin{equation*}{\textrm{Var}}\!\left(\bar{W}_{\alpha,r}\right)\ge C\big(\alpha r^{-d}\big)\vee\left(\alpha^{\frac{k\beta-2\beta-3dk+2d}{k\beta-2\beta-dk}}\right)\end{equation*}
 $R_0\le r\le \alpha^{1/d}/6$
, where
$R_0\le r\le \alpha^{1/d}/6$
, where
 $C,R_0>0$
are independent of
$C,R_0>0$
are independent of
 $\alpha$
.
$\alpha$
.
Proof of Theorem
2.2. Let
![]() $\sigma_{\alpha}^2\,:\!=\,{\textrm{Var}}\!\left(\bar{W}_{\alpha}\right)$
,
$\sigma_{\alpha}^2\,:\!=\,{\textrm{Var}}\!\left(\bar{W}_{\alpha}\right)$
,
![]() $\sigma_{\alpha,r}^2\,:\!=\,{\textrm{Var}}\!\left(\bar{W}_{\alpha,r}\right)$
, and
$\sigma_{\alpha,r}^2\,:\!=\,{\textrm{Var}}\!\left(\bar{W}_{\alpha,r}\right)$
, and
![]() $\bar{Z}_{\alpha,r}\sim N\!\left(\mathbb{E}\bar{W}_{\alpha,r}, \sigma_{\alpha,r}^2\right)$
; then it follows from the triangle inequality that
$\bar{Z}_{\alpha,r}\sim N\!\left(\mathbb{E}\bar{W}_{\alpha,r}, \sigma_{\alpha,r}^2\right)$
; then it follows from the triangle inequality that
We take
![]() $R_0$
as the maximum of the quantities
$R_0$
as the maximum of the quantities
![]() $R_0$
in Lemma 4.4(b), Corollary 4.1(b), and Lemma 5.9(b). We start with the exponentially stabilising case (ii).
$R_0$
in Lemma 4.4(b), Corollary 4.1(b), and Lemma 5.9(b). We start with the exponentially stabilising case (ii).
(ii) The first term of (5.54) can be bounded using Lemma 5.6(b), giving
for
![]() $r>C_3\ln\!(\alpha).$
$r>C_3\ln\!(\alpha).$
We can establish an upper bound for the second term
![]() $d_{TV}\left(\bar{Z}_\alpha,\bar{Z}_{\alpha,r}\right)$
of (5.54) using Lemma 5.1. To this end, (5.33) gives
$d_{TV}\left(\bar{Z}_\alpha,\bar{Z}_{\alpha,r}\right)$
of (5.54) using Lemma 5.1. To this end, (5.33) gives
which, together with Lemma 4.5(b), implies
for
![]() $r>C_4\ln\!(\alpha).$
We combine (5.57) and (5.38) to obtain
$r>C_4\ln\!(\alpha).$
We combine (5.57) and (5.38) to obtain
for
![]() $r>C_5\ln\!(\alpha).$
Therefore, it follows from (5.56), (5.57), (5.58), and Lemma 5.1 that
$r>C_5\ln\!(\alpha).$
Therefore, it follows from (5.56), (5.57), (5.58), and Lemma 5.1 that
for
![]() $r>C_6 \ln\!(\alpha).$
$r>C_6 \ln\!(\alpha).$
For the last term of (5.54), as a linear transformation does not change the total variation distance, we can rewrite it as
where
![]() $V_{\alpha,r}\,:\!=\,\left(\bar{W}_{\alpha,r}-\mathbb{E} \bar{W}_{\alpha,r}\right)/\sigma_{\alpha,r}$
and
$V_{\alpha,r}\,:\!=\,\left(\bar{W}_{\alpha,r}-\mathbb{E} \bar{W}_{\alpha,r}\right)/\sigma_{\alpha,r}$
and
![]() $Z\sim N(0,1)$
. We now appeal to Stein’s method to tackle the problem. Briefly speaking, Stein’s method for normal approximation hinges on a Stein equation (see [Reference Chen, Goldstein and Shao10, p. 15])
$Z\sim N(0,1)$
. We now appeal to Stein’s method to tackle the problem. Briefly speaking, Stein’s method for normal approximation hinges on a Stein equation (see [Reference Chen, Goldstein and Shao10, p. 15])
where
![]() $Nh\,:\!=\,\mathbb{E} h(Z)$
. The solution of (5.61) satisfies (see [Reference Chen, Goldstein and Shao10, p. 16])
$Nh\,:\!=\,\mathbb{E} h(Z)$
. The solution of (5.61) satisfies (see [Reference Chen, Goldstein and Shao10, p. 16])
Hence, for
![]() $h={\textbf{1}}_A$
with
$h={\textbf{1}}_A$
with
![]() $A\in{\mathscr{B}}(\mathbb{R})$
, the solution
$A\in{\mathscr{B}}(\mathbb{R})$
, the solution
![]() $f_h\,=\!:\,f_A$
satisfies
$f_h\,=\!:\,f_A$
satisfies
The Stein equation (5.61) enables us to bound
![]() $d_{TV}\left(V_{\alpha,r},Z\right)$
through a functional form of
$d_{TV}\left(V_{\alpha,r},Z\right)$
through a functional form of
![]() $V_{\alpha,r}$
only, giving
$V_{\alpha,r}$
only, giving
Recalling (5.48) and (5.49), we can represent
![]() $V_{\alpha,r}$
through
$V_{\alpha,r}$
through
![]() $V(dx)\,:\!=\,\frac{1}{\sigma_{\alpha,r}}\bar{\Xi}_\alpha^\ast(dx),$
giving
$V(dx)\,:\!=\,\frac{1}{\sigma_{\alpha,r}}\bar{\Xi}_\alpha^\ast(dx),$
giving
![]() $V_{\alpha,r}=\int_{\Gamma_\alpha}V(dx)$
. Let
$V_{\alpha,r}=\int_{\Gamma_\alpha}V(dx)$
. Let
![]() $N^{\prime}_{x,\alpha, r}=B(x,2r)\cap\Gamma_\alpha$
and
$N^{\prime}_{x,\alpha, r}=B(x,2r)\cap\Gamma_\alpha$
and
![]() $N^{\prime\prime}_{x,\alpha, r}=B(x,4r)\cap\Gamma_\alpha$
. Define
$N^{\prime\prime}_{x,\alpha, r}=B(x,4r)\cap\Gamma_\alpha$
. Define
Since V(dx) is independent of V(dy) if
![]() $|x-y|>2r$
, V(dx) is independent of
$|x-y|>2r$
, V(dx) is independent of
![]() $V_{\alpha,r}-S^{\prime}_{x,\alpha,r}$
,
$V_{\alpha,r}-S^{\prime}_{x,\alpha,r}$
,
![]() $S^{\prime}_{x,\alpha,r}V(dx)$
is independent of
$S^{\prime}_{x,\alpha,r}V(dx)$
is independent of
![]() $V_{\alpha,r}-S^{\prime\prime}_{x,\alpha,r}$
,
$V_{\alpha,r}-S^{\prime\prime}_{x,\alpha,r}$
,
![]() $1={\textrm{Var}}\!\left(V_{\alpha,r}\right)=\mathbb{E}\int_{\Gamma_\alpha} S^{\prime}_{x,\alpha,r}V(dx)$
, and
$1={\textrm{Var}}\!\left(V_{\alpha,r}\right)=\mathbb{E}\int_{\Gamma_\alpha} S^{\prime}_{x,\alpha,r}V(dx)$
, and
 \begin{align} &\quad \mathbb{E}\!\left[f^{\prime}\left(V_{\alpha,r}\right)-V_{\alpha,r}f\!\left(V_{\alpha,r}\right)\right]\nonumber \\&=\mathbb{E}f^{\prime}\left(V_{\alpha,r}\right) -\mathbb{E}\int_{\Gamma_\alpha}\left(f(V_{\alpha,r})-f\!\left(V_{\alpha,r}-S^{\prime}_{x,\alpha,r}\right)\right)V(dx)\nonumber \\&=\mathbb{E}f^{\prime}\left(V_{\alpha,r}\right) - \mathbb{E}\int_{\Gamma_\alpha}\int_{0}^1f^{\prime}\left(V_{\alpha,r}-uS^{\prime}_{x,\alpha,r}\right)S^{\prime}_{x,\alpha,r}du V(dx)\nonumber \\&={\mathbb{E}\int_{\Gamma_\alpha}\mathbb{E}\!\left[f^{\prime}\left(V_{\alpha,r}\right)\right]S^{\prime}_{x,\alpha, r}V(dx) - \mathbb{E}\int_{\Gamma_\alpha}\int_{0}^1f^{\prime}\left(V_{\alpha,r}-uS^{\prime}_{x,\alpha,r}\right)S^{\prime}_{x,\alpha,r}du V(dx)\nonumber} \\&=\mathbb{E}\int_{\Gamma_\alpha}\mathbb{E}\!\left[f^{\prime}\left(V_{\alpha,r}\right)-f^{\prime}\left(V_{\alpha,r}-S^{\prime\prime}_{x,\alpha,r}\right)\right]S^{\prime}_{x,\alpha, r}V(dx)\nonumber \\&\quad -\mathbb{E}\int_{\Gamma_\alpha}\int_{0}^1\left(f^{\prime}\left(V_{\alpha,r}-uS^{\prime}_{x,\alpha,r}\right)-f^{\prime}\left(V_{\alpha,r}-S^{\prime\prime}_{x,\alpha,r}\right)\right)S^{\prime}_{x,\alpha, r}du V(dx).\end{align}
\begin{align} &\quad \mathbb{E}\!\left[f^{\prime}\left(V_{\alpha,r}\right)-V_{\alpha,r}f\!\left(V_{\alpha,r}\right)\right]\nonumber \\&=\mathbb{E}f^{\prime}\left(V_{\alpha,r}\right) -\mathbb{E}\int_{\Gamma_\alpha}\left(f(V_{\alpha,r})-f\!\left(V_{\alpha,r}-S^{\prime}_{x,\alpha,r}\right)\right)V(dx)\nonumber \\&=\mathbb{E}f^{\prime}\left(V_{\alpha,r}\right) - \mathbb{E}\int_{\Gamma_\alpha}\int_{0}^1f^{\prime}\left(V_{\alpha,r}-uS^{\prime}_{x,\alpha,r}\right)S^{\prime}_{x,\alpha,r}du V(dx)\nonumber \\&={\mathbb{E}\int_{\Gamma_\alpha}\mathbb{E}\!\left[f^{\prime}\left(V_{\alpha,r}\right)\right]S^{\prime}_{x,\alpha, r}V(dx) - \mathbb{E}\int_{\Gamma_\alpha}\int_{0}^1f^{\prime}\left(V_{\alpha,r}-uS^{\prime}_{x,\alpha,r}\right)S^{\prime}_{x,\alpha,r}du V(dx)\nonumber} \\&=\mathbb{E}\int_{\Gamma_\alpha}\mathbb{E}\!\left[f^{\prime}\left(V_{\alpha,r}\right)-f^{\prime}\left(V_{\alpha,r}-S^{\prime\prime}_{x,\alpha,r}\right)\right]S^{\prime}_{x,\alpha, r}V(dx)\nonumber \\&\quad -\mathbb{E}\int_{\Gamma_\alpha}\int_{0}^1\left(f^{\prime}\left(V_{\alpha,r}-uS^{\prime}_{x,\alpha,r}\right)-f^{\prime}\left(V_{\alpha,r}-S^{\prime\prime}_{x,\alpha,r}\right)\right)S^{\prime}_{x,\alpha, r}du V(dx).\end{align}
By the definition of the total variation distance, we have
for any
![]() $\gamma\in \mathbb{R}$
. Using Corollary 4.1(b) with
$\gamma\in \mathbb{R}$
. Using Corollary 4.1(b) with
![]() $N_{\alpha,r}^{(1)}=N_{\alpha,r}^{(3)}\,:\!=\,\emptyset$
and
$N_{\alpha,r}^{(1)}=N_{\alpha,r}^{(3)}\,:\!=\,\emptyset$
and
![]() $N_{\alpha,r}^{(2)}\,:\!=\,B\!\left(N^{\prime\prime}_{x,\alpha,r},r\right)$
, for
$N_{\alpha,r}^{(2)}\,:\!=\,B\!\left(N^{\prime\prime}_{x,\alpha,r},r\right)$
, for
![]() $r\le C_7 \alpha^{\frac{1}{d}}$
, the non-singularity in Assumption 2.4 ensures that
$r\le C_7 \alpha^{\frac{1}{d}}$
, the non-singularity in Assumption 2.4 ensures that
which, together with (5.65), implies
Recalling (5.49), we have
Using the first-order Palm distribution (5.4), the third-order Palm distribution (5.6), and the moment condition (2.4), we obtain
 \begin{align*} &\mathbb{E}\!\left[\left|{g_\alpha\!\left(z,\Xi\right)}\right|\textbf{1}_{\bar{R}(z,\alpha)<r}\bar{\Xi}(dz)\left|{g_\alpha\!\left(y,\Xi\right)}\right|\textbf{1}_{\bar{R}(y,\alpha)<r}\bar{\Xi}(dy)\left|{g_\alpha\!\left(x,\Xi\right)}\right|\textbf{1}_{\bar{R}(x,\alpha)<r}\bar{\Xi}(dx)\right]\\ &\ \ \ \le C_8 \left(\lambda^3 dzdydx+\lambda^2dzdx+\lambda^2dydx+\lambda dx\right),\\ &\mathbb{E}\!\left[\left|{g_\alpha\!\left(y,\Xi\right)}\right|\textbf{1}_{\bar{R}(y,\alpha)<r}\bar{\Xi}(dy)\right]\le C_1 \lambda dy, \\ &\left|P_{y,\alpha,r}\right|\le C_1 \lambda,\end{align*}
\begin{align*} &\mathbb{E}\!\left[\left|{g_\alpha\!\left(z,\Xi\right)}\right|\textbf{1}_{\bar{R}(z,\alpha)<r}\bar{\Xi}(dz)\left|{g_\alpha\!\left(y,\Xi\right)}\right|\textbf{1}_{\bar{R}(y,\alpha)<r}\bar{\Xi}(dy)\left|{g_\alpha\!\left(x,\Xi\right)}\right|\textbf{1}_{\bar{R}(x,\alpha)<r}\bar{\Xi}(dx)\right]\\ &\ \ \ \le C_8 \left(\lambda^3 dzdydx+\lambda^2dzdx+\lambda^2dydx+\lambda dx\right),\\ &\mathbb{E}\!\left[\left|{g_\alpha\!\left(y,\Xi\right)}\right|\textbf{1}_{\bar{R}(y,\alpha)<r}\bar{\Xi}(dy)\right]\le C_1 \lambda dy, \\ &\left|P_{y,\alpha,r}\right|\le C_1 \lambda,\end{align*}
which, together with (5.51) and (5.52), yields
Since
![]() $N^{\prime\prime}_{x,\alpha, r}\subset B(x,4r)$
, the volume of
$N^{\prime\prime}_{x,\alpha, r}\subset B(x,4r)$
, the volume of
![]() $N^{\prime\prime}_{x,\alpha, r}$
is of order
$N^{\prime\prime}_{x,\alpha, r}$
is of order
![]() $\mathop{{}\textrm{O}}\mathopen{}(r^d)$
. Then
$\mathop{{}\textrm{O}}\mathopen{}(r^d)$
. Then
 \begin{align} &\mathbb{E}\int_{N^{\prime}_{x,\alpha, r}} \left|\bar{\Xi}_\alpha^\ast(dy)\right|\le \mathbb{E}\int_{N^{\prime\prime}_{x,\alpha, r}} \left|\bar{\Xi}_\alpha^\ast(dy)\right|\le \mathop{{}\textrm{O}}\mathopen{}\big(r^d\big),\nonumber\\ &\mathbb{E}\!\left[\left|\sigma_{\alpha,r}S^{\prime\prime}_{x,\alpha,r}\right|\vee 1\right] \le 1+\mathbb{E}\int_{N^{\prime\prime}_{x,\alpha, r}} \left|\bar{\Xi}_\alpha^\ast(dy)\right|\le \mathop{{}\textrm{O}}\mathopen{}\big(r^d\big).\end{align}
\begin{align} &\mathbb{E}\int_{N^{\prime}_{x,\alpha, r}} \left|\bar{\Xi}_\alpha^\ast(dy)\right|\le \mathbb{E}\int_{N^{\prime\prime}_{x,\alpha, r}} \left|\bar{\Xi}_\alpha^\ast(dy)\right|\le \mathop{{}\textrm{O}}\mathopen{}\big(r^d\big),\nonumber\\ &\mathbb{E}\!\left[\left|\sigma_{\alpha,r}S^{\prime\prime}_{x,\alpha,r}\right|\vee 1\right] \le 1+\mathbb{E}\int_{N^{\prime\prime}_{x,\alpha, r}} \left|\bar{\Xi}_\alpha^\ast(dy)\right|\le \mathop{{}\textrm{O}}\mathopen{}\big(r^d\big).\end{align}
Combining (5.66), (5.70), and (5.62), we have
Hence the first term of (5.64) can be bounded as
 \begin{align} &\left|\mathbb{E}\int_{\Gamma_\alpha}\mathbb{E}\!\left[f^{\prime}\left(V_{\alpha,r}\right)-f^{\prime}\left(V_{\alpha,r}-S^{\prime\prime}_{x,\alpha,r} \right)\right]S^{\prime}_{x,\alpha, r} V(dx)\right|\nonumber \\ \le &\mathop{{}\textrm{O}}\mathopen{}\left(\alpha^{-\frac{1}{2}}r^{\frac{3d}{2}}\right)\sigma_{\alpha,r}^{-2}\mathbb{E}\int_{\Gamma_\alpha}\int_{N^{\prime}_{x,\alpha, r}}\left|\bar{\Xi}_\alpha^\ast(dy)\right|\left|\bar{\Xi}_\alpha^\ast(dx)\right|\nonumber \\ \le &\mathop{{}\textrm{O}}\mathopen{}\left(\alpha^{-\frac{1}{2}}r^{\frac{3d}{2}}\right)\sigma_{\alpha,r}^{-2}\int_{\Gamma_\alpha}\left(\int_{N^{\prime}_{x,\alpha, r}} \lambda dy+1\right)\lambda dx = {\mathop{{}\textrm{O}}\mathopen{}\left(\sigma_{\alpha,r}^{-2}\alpha^{\frac{1}{2}}r^{\frac{5d}{2}}\right)},\end{align}
\begin{align} &\left|\mathbb{E}\int_{\Gamma_\alpha}\mathbb{E}\!\left[f^{\prime}\left(V_{\alpha,r}\right)-f^{\prime}\left(V_{\alpha,r}-S^{\prime\prime}_{x,\alpha,r} \right)\right]S^{\prime}_{x,\alpha, r} V(dx)\right|\nonumber \\ \le &\mathop{{}\textrm{O}}\mathopen{}\left(\alpha^{-\frac{1}{2}}r^{\frac{3d}{2}}\right)\sigma_{\alpha,r}^{-2}\mathbb{E}\int_{\Gamma_\alpha}\int_{N^{\prime}_{x,\alpha, r}}\left|\bar{\Xi}_\alpha^\ast(dy)\right|\left|\bar{\Xi}_\alpha^\ast(dx)\right|\nonumber \\ \le &\mathop{{}\textrm{O}}\mathopen{}\left(\alpha^{-\frac{1}{2}}r^{\frac{3d}{2}}\right)\sigma_{\alpha,r}^{-2}\int_{\Gamma_\alpha}\left(\int_{N^{\prime}_{x,\alpha, r}} \lambda dy+1\right)\lambda dx = {\mathop{{}\textrm{O}}\mathopen{}\left(\sigma_{\alpha,r}^{-2}\alpha^{\frac{1}{2}}r^{\frac{5d}{2}}\right)},\end{align}
where the last inequality is from (5.68), and the last equality follows from the fact that
![]() $\mbox{Vol}(N^{\prime}_{x,\alpha, r})\le \mbox{Vol}\left(B(x,2r)\right)=\mathop{{}\textrm{O}}\mathopen{}(r^d)$
.
$\mbox{Vol}(N^{\prime}_{x,\alpha, r})\le \mbox{Vol}\left(B(x,2r)\right)=\mathop{{}\textrm{O}}\mathopen{}(r^d)$
.
For the second term of (5.64), we have from Corollary 4.1 with
![]() $N_{\alpha,r}^{(1)}\,:\!=\,B\!\left(N^{\prime}_{x,\alpha,r},r\right)$
,
$N_{\alpha,r}^{(1)}\,:\!=\,B\!\left(N^{\prime}_{x,\alpha,r},r\right)$
,
![]() $N_{\alpha,r}^{(2)}\,:\!=\,B\!\left(N^{\prime\prime}_{x,\alpha,r},r\right)$
,
$N_{\alpha,r}^{(2)}\,:\!=\,B\!\left(N^{\prime\prime}_{x,\alpha,r},r\right)$
,
![]() $N_{\alpha,r}^{(3)}\,:\!=\,N^{\prime\prime}_{x,\alpha,r}$
, for
$N_{\alpha,r}^{(3)}\,:\!=\,N^{\prime\prime}_{x,\alpha,r}$
, for
![]() $r\le C_14 \alpha^{\frac{1}{d}}$
, and the non-singularity in Assumption 2.4 that
$r\le C_14 \alpha^{\frac{1}{d}}$
, and the non-singularity in Assumption 2.4 that
 \begin{align} &\left|\mathbb{E}\!\left[\left.\int_{0}^1\left(f^{\prime}\left(V_{\alpha,r}-uS^{\prime}_{x,\alpha,r}\right)-f^{\prime}\left(V_{\alpha,r}-S^{\prime\prime}_{x,\alpha,r}\right)\right)du\right|\Xi_{{B\!\left(N^{\prime}_{x,\alpha,r},r\right)}}\right]\right|\nonumber\\ \le&2\int_{0}^{1}\mathbb{E}d_{TV}\left(\left.V_{\alpha,r}-uS^{\prime}_{x,\alpha,r},V_{\alpha,r}-S^{\prime\prime}_{x,\alpha,r}\right|\Xi_{{B\!\left(N^{\prime}_{x,\alpha,r},r\right)}} \right) du\nonumber \\\le&\mathop{{}\textrm{O}}\mathopen{}\left(\alpha^{-\frac{1}{2}}r^{\frac{d}{2}}\right)\mathbb{E}\!\left(\left.\int_{N^{\prime\prime}_{x,\alpha, r}}\left|\bar{\Xi}_\alpha^\ast(dz)\right|+ 1\right|\Xi_{{B\!\left(N^{\prime}_{x,\alpha,r},r\right)}}\right);\nonumber\end{align}
\begin{align} &\left|\mathbb{E}\!\left[\left.\int_{0}^1\left(f^{\prime}\left(V_{\alpha,r}-uS^{\prime}_{x,\alpha,r}\right)-f^{\prime}\left(V_{\alpha,r}-S^{\prime\prime}_{x,\alpha,r}\right)\right)du\right|\Xi_{{B\!\left(N^{\prime}_{x,\alpha,r},r\right)}}\right]\right|\nonumber\\ \le&2\int_{0}^{1}\mathbb{E}d_{TV}\left(\left.V_{\alpha,r}-uS^{\prime}_{x,\alpha,r},V_{\alpha,r}-S^{\prime\prime}_{x,\alpha,r}\right|\Xi_{{B\!\left(N^{\prime}_{x,\alpha,r},r\right)}} \right) du\nonumber \\\le&\mathop{{}\textrm{O}}\mathopen{}\left(\alpha^{-\frac{1}{2}}r^{\frac{d}{2}}\right)\mathbb{E}\!\left(\left.\int_{N^{\prime\prime}_{x,\alpha, r}}\left|\bar{\Xi}_\alpha^\ast(dz)\right|+ 1\right|\Xi_{{B\!\left(N^{\prime}_{x,\alpha,r},r\right)}}\right);\nonumber\end{align}
hence
 \begin{align} &\left|\mathbb{E}\int_{\Gamma_\alpha}\int_{0}^1\left(f^{\prime}\left(V_{\alpha,r}-uS^{\prime}_{x,\alpha,r}\right)-f^{\prime}\left(V_{\alpha,r}-S^{\prime\prime}_{x,\alpha,r}\right)\right)S^{\prime}_{x,\alpha, r}du V(dx)\right|\nonumber\\ =&\left|\mathbb{E}\int_{\Gamma_\alpha}\mathbb{E}\!\left[\left.\int_{0}^1\left(f^{\prime}\left(V_{\alpha,r}-uS^{\prime}_{x,\alpha,r}\right)-f^{\prime}\left(V_{\alpha,r}-S^{\prime\prime}_{x,\alpha,r}\right)\right)du\right|\Xi_{B\!\left(N^{\prime}_{x,\alpha,r},r\right)}\right]S^{\prime}_{x,\alpha, r} V(dx)\right|\nonumber\\ \le& \mathop{{}\textrm{O}}\mathopen{}\left(\alpha^{-\frac{1}{2}}r^{\frac{d}{2}}\right)\mathbb{E}\int_{\Gamma_\alpha}\mathbb{E}\!\left(\left.\int_{N^{\prime\prime}_{x,\alpha, r}}\left|\bar{\Xi}_\alpha^\ast(dz)\right|+ 1\right|\Xi_{B\!\left(N^{\prime}_{x,\alpha,r},r\right)}\right)\left|S^{\prime}_{x,\alpha, r}\right| |V(dx)|\nonumber\\ \le& \mathop{{}\textrm{O}}\mathopen{}\left(\alpha^{-\frac{1}{2}}r^{\frac{d}{2}}\right)\sigma_{\alpha,r}^{-2}\mathbb{E}\int_{\Gamma_\alpha}\left[\int_{N^{\prime\prime}_{x,\alpha, r}}\int_{N^{\prime}_{x,\alpha, r}}\left|\bar{\Xi}_\alpha^\ast(dz)\bar{\Xi}_\alpha^\ast(dy)\right|+\int_{N^{\prime}_{x,\alpha, r}}\left|\bar{\Xi}_\alpha^\ast(dy)\right|\right]\left|\bar{\Xi}_\alpha^\ast(dx)\right|\nonumber\\ \le& \mathop{{}\textrm{O}}\mathopen{}\left(\alpha^{-\frac{1}{2}}r^{\frac{d}{2}}\right)\sigma_{\alpha,r}^{-2}\int_{\Gamma_\alpha}\left(\int_{N^{\prime\prime}_{x,\alpha, r}}\int_{N^{\prime}_{x,\alpha, r}}\lambda^2dzdy+\int_{N^{\prime\prime}_{x,\alpha, r}}\lambda dz+\int_{N^{\prime}_{x,\alpha, r}}\lambda dy+1\right)\lambda dx\nonumber\\ \le& \mathop{{}\textrm{O}}\mathopen{}\left(\alpha^{-\frac{1}{2}}r^{\frac{d}{2}}\right)\sigma_{\alpha,r}^{-2}\mathop{{}\textrm{O}}\mathopen{}\big(\alpha r^{2d}\big)\nonumber\\ =& \mathop{{}\textrm{O}}\mathopen{}\left(\sigma_{\alpha,r}^{-2}\alpha^{\frac{1}{2}}r^{\frac{5d}{2}}\right),\end{align}
\begin{align} &\left|\mathbb{E}\int_{\Gamma_\alpha}\int_{0}^1\left(f^{\prime}\left(V_{\alpha,r}-uS^{\prime}_{x,\alpha,r}\right)-f^{\prime}\left(V_{\alpha,r}-S^{\prime\prime}_{x,\alpha,r}\right)\right)S^{\prime}_{x,\alpha, r}du V(dx)\right|\nonumber\\ =&\left|\mathbb{E}\int_{\Gamma_\alpha}\mathbb{E}\!\left[\left.\int_{0}^1\left(f^{\prime}\left(V_{\alpha,r}-uS^{\prime}_{x,\alpha,r}\right)-f^{\prime}\left(V_{\alpha,r}-S^{\prime\prime}_{x,\alpha,r}\right)\right)du\right|\Xi_{B\!\left(N^{\prime}_{x,\alpha,r},r\right)}\right]S^{\prime}_{x,\alpha, r} V(dx)\right|\nonumber\\ \le& \mathop{{}\textrm{O}}\mathopen{}\left(\alpha^{-\frac{1}{2}}r^{\frac{d}{2}}\right)\mathbb{E}\int_{\Gamma_\alpha}\mathbb{E}\!\left(\left.\int_{N^{\prime\prime}_{x,\alpha, r}}\left|\bar{\Xi}_\alpha^\ast(dz)\right|+ 1\right|\Xi_{B\!\left(N^{\prime}_{x,\alpha,r},r\right)}\right)\left|S^{\prime}_{x,\alpha, r}\right| |V(dx)|\nonumber\\ \le& \mathop{{}\textrm{O}}\mathopen{}\left(\alpha^{-\frac{1}{2}}r^{\frac{d}{2}}\right)\sigma_{\alpha,r}^{-2}\mathbb{E}\int_{\Gamma_\alpha}\left[\int_{N^{\prime\prime}_{x,\alpha, r}}\int_{N^{\prime}_{x,\alpha, r}}\left|\bar{\Xi}_\alpha^\ast(dz)\bar{\Xi}_\alpha^\ast(dy)\right|+\int_{N^{\prime}_{x,\alpha, r}}\left|\bar{\Xi}_\alpha^\ast(dy)\right|\right]\left|\bar{\Xi}_\alpha^\ast(dx)\right|\nonumber\\ \le& \mathop{{}\textrm{O}}\mathopen{}\left(\alpha^{-\frac{1}{2}}r^{\frac{d}{2}}\right)\sigma_{\alpha,r}^{-2}\int_{\Gamma_\alpha}\left(\int_{N^{\prime\prime}_{x,\alpha, r}}\int_{N^{\prime}_{x,\alpha, r}}\lambda^2dzdy+\int_{N^{\prime\prime}_{x,\alpha, r}}\lambda dz+\int_{N^{\prime}_{x,\alpha, r}}\lambda dy+1\right)\lambda dx\nonumber\\ \le& \mathop{{}\textrm{O}}\mathopen{}\left(\alpha^{-\frac{1}{2}}r^{\frac{d}{2}}\right)\sigma_{\alpha,r}^{-2}\mathop{{}\textrm{O}}\mathopen{}\big(\alpha r^{2d}\big)\nonumber\\ =& \mathop{{}\textrm{O}}\mathopen{}\left(\sigma_{\alpha,r}^{-2}\alpha^{\frac{1}{2}}r^{\frac{5d}{2}}\right),\end{align}
where the second-to-last inequality follows from (5.67), (5.68), and (5.69), and the last inequality is due to the fact that the volumes of
![]() $N^{\prime}_{x,\alpha, r}$
and
$N^{\prime}_{x,\alpha, r}$
and
![]() $N^{\prime\prime}_{x,\alpha, r}$
are of order
$N^{\prime\prime}_{x,\alpha, r}$
are of order
![]() $\mathop{{}\textrm{O}}\mathopen{}\big(r^d\big)$
. Recalling (5.63) and (5.64), we add up the bounds of (5.71) and (5.72) to obtain
$\mathop{{}\textrm{O}}\mathopen{}\big(r^d\big)$
. Recalling (5.63) and (5.64), we add up the bounds of (5.71) and (5.72) to obtain
The proof of (ii) is completed by using (5.54), taking
![]() $r={\max\!(C_{3},C_{4},C_{5})}\ln\!(\alpha)$
for large
$r={\max\!(C_{3},C_{4},C_{5})}\ln\!(\alpha)$
for large
![]() $\alpha$
, and collecting the bounds in (5.55), (5.60), and (5.73) and substituting
$\alpha$
, and collecting the bounds in (5.55), (5.60), and (5.73) and substituting
![]() $\sigma_{\alpha,r}^{2}=\Omega(\alpha)$
, as shown in (5.57).
$\sigma_{\alpha,r}^{2}=\Omega(\alpha)$
, as shown in (5.57).
(i) There exists an
![]() $r_1>0$
such that
$r_1>0$
such that
![]() $\bar{W}_{\alpha,r_1}= \bar{W}_{\alpha}$
a.s. for all
$\bar{W}_{\alpha,r_1}= \bar{W}_{\alpha}$
a.s. for all
![]() $\alpha$
, which implies
$\alpha$
, which implies
![]() $\mathbb{E} \bar{W}_{\alpha,r_1}=\mathbb{E} \bar{W}_{\alpha}$
,
$\mathbb{E} \bar{W}_{\alpha,r_1}=\mathbb{E} \bar{W}_{\alpha}$
,
![]() ${\textrm{Var}}\!\left(\bar{W}_{\alpha,r_1}\right)={\textrm{Var}}\!\left(\bar{W}_{\alpha}\right)$
; hence
${\textrm{Var}}\!\left(\bar{W}_{\alpha,r_1}\right)={\textrm{Var}}\!\left(\bar{W}_{\alpha}\right)$
; hence
![]() $d_{TV}\big(\bar{W}_{\alpha},\bar{Z}_\alpha\big)= d_{TV}\big(\bar{W}_{\alpha,r_1},\bar{Z}_{\alpha,r_1}\big)$
. On the other hand, range-boundedness implies exponential stabilisation; with
$d_{TV}\big(\bar{W}_{\alpha},\bar{Z}_\alpha\big)= d_{TV}\big(\bar{W}_{\alpha,r_1},\bar{Z}_{\alpha,r_1}\big)$
. On the other hand, range-boundedness implies exponential stabilisation; with
![]() $r_1$
in place of r, (5.57) and (5.73) still hold. However,
$r_1$
in place of r, (5.57) and (5.73) still hold. However,
![]() $r_1$
is a constant independent of
$r_1$
is a constant independent of
![]() $\alpha$
; the conclusion follows.
$\alpha$
; the conclusion follows.
(iii) We take
![]() $r=r_\alpha\,:\!=\, R_0\vee \alpha^{\frac{5k-4}{5dk+2\beta k -4\beta}}$
. Lemma 5.6(b) gives
$r=r_\alpha\,:\!=\, R_0\vee \alpha^{\frac{5k-4}{5dk+2\beta k -4\beta}}$
. Lemma 5.6(b) gives
Next, applying Lemma 4.6(b) and Lemma 5.10(b), we have
which, together with (5.34), (5.41), and (5.59), yields
 \begin{equation} d_{TV}\big(\bar{Z}_\alpha,\bar{Z}_{\alpha,r}\big)\le \mathop{{}\textrm{O}}\mathopen{}\left(\frac{\alpha^{\frac{2k-1}k}r^{-\beta\frac{k-1}k}}{\alpha^{\frac12\frac{k\beta-2\beta-3dk+2d}{k\beta-2\beta-dk}}}\vee\frac{\alpha^{\frac{3k-2}k}r^{-\beta\frac{k-2}k}}{\alpha^{\frac{k\beta-2\beta-3dk+2d}{k\beta-2\beta-dk}}}\vee\frac{\alpha^{\frac{3k-1}k}r^{-\beta\frac{k-1}k}}{\alpha^{\frac{k\beta-2\beta-3dk+2d}{k\beta-2\beta-dk}}}\right)\end{equation}
\begin{equation} d_{TV}\big(\bar{Z}_\alpha,\bar{Z}_{\alpha,r}\big)\le \mathop{{}\textrm{O}}\mathopen{}\left(\frac{\alpha^{\frac{2k-1}k}r^{-\beta\frac{k-1}k}}{\alpha^{\frac12\frac{k\beta-2\beta-3dk+2d}{k\beta-2\beta-dk}}}\vee\frac{\alpha^{\frac{3k-2}k}r^{-\beta\frac{k-2}k}}{\alpha^{\frac{k\beta-2\beta-3dk+2d}{k\beta-2\beta-dk}}}\vee\frac{\alpha^{\frac{3k-1}k}r^{-\beta\frac{k-1}k}}{\alpha^{\frac{k\beta-2\beta-3dk+2d}{k\beta-2\beta-dk}}}\right)\end{equation}
for
![]() $R_0< r< C_15 \alpha^{\frac{1}{d}}$
. Recalling that
$R_0< r< C_15 \alpha^{\frac{1}{d}}$
. Recalling that
![]() $\beta>\frac{(15k-14)d}{k-2}$
, the dominating term of (5.76) is
$\beta>\frac{(15k-14)d}{k-2}$
, the dominating term of (5.76) is
 \begin{equation*}\frac{\alpha^{\frac{3k-2}k}r^{-\beta\frac{k-2}k}}{\alpha^{\frac{k\beta-2\beta-3dk+2d}{k\beta-2\beta-dk}}},\end{equation*}
\begin{equation*}\frac{\alpha^{\frac{3k-2}k}r^{-\beta\frac{k-2}k}}{\alpha^{\frac{k\beta-2\beta-3dk+2d}{k\beta-2\beta-dk}}},\end{equation*}
giving
 \begin{equation} d_{TV}\big(\bar{Z}_\alpha,\bar{Z}_{\alpha,r}\big)\le \mathop{{}\textrm{O}}\mathopen{}\left(\frac{\alpha^{\frac{3k-2}k}r^{-\beta\frac{k-2}k}}{\alpha^{\frac{k\beta-2\beta-3dk+2d}{k\beta-2\beta-dk}}}\right)=\mathop{{}\textrm{O}}\mathopen{}\left(\alpha^{-\frac{\beta(k-2)[\beta(k-2)-d(15k-14)]}{(k\beta-2\beta-dk)(5dk+2\beta k-4\beta)}}\right).\end{equation}
\begin{equation} d_{TV}\big(\bar{Z}_\alpha,\bar{Z}_{\alpha,r}\big)\le \mathop{{}\textrm{O}}\mathopen{}\left(\frac{\alpha^{\frac{3k-2}k}r^{-\beta\frac{k-2}k}}{\alpha^{\frac{k\beta-2\beta-3dk+2d}{k\beta-2\beta-dk}}}\right)=\mathop{{}\textrm{O}}\mathopen{}\left(\alpha^{-\frac{\beta(k-2)[\beta(k-2)-d(15k-14)]}{(k\beta-2\beta-dk)(5dk+2\beta k-4\beta)}}\right).\end{equation}
For
![]() $d_{TV}\big(\bar{W}_{\alpha,r},\bar{Z}_{\alpha,r}\big)$
, we make use of (5.73) and (5.75), and replace r with
$d_{TV}\big(\bar{W}_{\alpha,r},\bar{Z}_{\alpha,r}\big)$
, we make use of (5.73) and (5.75), and replace r with
![]() $r_\alpha$
to obtain
$r_\alpha$
to obtain
Finally, the proof is completed by combining (5.54), (5.74), (5.77), and (5.78).
Proof of Theorem
2.1. One can repeat the proof of Theorem 2.2 by replacing
![]() $\bar{W}_\alpha$
,
$\bar{W}_\alpha$
,
![]() $\bar{W}_{\alpha,r}$
,
$\bar{W}_{\alpha,r}$
,
![]() $\bar{Z}_\alpha$
,
$\bar{Z}_\alpha$
,
![]() $\bar{Z}_{\alpha,r}$
,
$\bar{Z}_{\alpha,r}$
,
![]() $g_\alpha(x,\Xi)$
, and
$g_\alpha(x,\Xi)$
, and
![]() $\bar{R}(x,\alpha)$
with
$\bar{R}(x,\alpha)$
with
![]() $W_\alpha$
,
$W_\alpha$
,
![]() $W_{\alpha,r}$
,
$W_{\alpha,r}$
,
![]() $Z_\alpha$
,
$Z_\alpha$
,
![]() $Z_{\alpha,r}$
,
$Z_{\alpha,r}$
,
![]() $g(\Xi^x)$
, and R(x).
$g(\Xi^x)$
, and R(x).
Remark 5.2. If we aim to find the order of the total variation distance between
![]() $\bar{W}_{\alpha}$
and a normal distribution instead of a normal distribution with the same mean and variance in the polynomially stabilising case, we can get a better upper-bound approximation error with a weaker condition. When
$\bar{W}_{\alpha}$
and a normal distribution instead of a normal distribution with the same mean and variance in the polynomially stabilising case, we can get a better upper-bound approximation error with a weaker condition. When
combining (5.73) and the fact that
![]() $d_{TV}\big(\bar{W}_{\alpha}, \bar{W}_{\alpha,r}\big)\le C\alpha\lambda r^{-\beta}$
, and taking
$d_{TV}\big(\bar{W}_{\alpha}, \bar{W}_{\alpha,r}\big)\le C\alpha\lambda r^{-\beta}$
, and taking
we have
 \begin{align*} d_{TV}\big(\bar{W}_{\alpha},\bar{Z}_{\alpha,r_\alpha}\big) &\le d_{TV}\big(\bar{W}_{\alpha},\bar{W}_{\alpha,r_\alpha}\big)+d_{TV}\big(\bar{W}_{\alpha,r_\alpha},\bar{Z}_{\alpha,r_\alpha}\big)\\ &\le \mathop{{}\textrm{O}}\mathopen{}\left(\alpha^{\frac{-\beta^2(k-2)+10\beta dk-14\beta d-5d^2k}{(\beta k-dk-2\beta)(5d+2\beta)}}\right). \end{align*}
\begin{align*} d_{TV}\big(\bar{W}_{\alpha},\bar{Z}_{\alpha,r_\alpha}\big) &\le d_{TV}\big(\bar{W}_{\alpha},\bar{W}_{\alpha,r_\alpha}\big)+d_{TV}\big(\bar{W}_{\alpha,r_\alpha},\bar{Z}_{\alpha,r_\alpha}\big)\\ &\le \mathop{{}\textrm{O}}\mathopen{}\left(\alpha^{\frac{-\beta^2(k-2)+10\beta dk-14\beta d-5d^2k}{(\beta k-dk-2\beta)(5d+2\beta)}}\right). \end{align*}
Acknowledgements
We wish to thank the referees for their suggestions, which led to an improved version of the paper. We also thank Vlad Bally for bringing to our attention his work with Lucia Caramellino.
Funding information
T. Cong is supported by a Research Training Program Scholarship and a Xing Lei Cross-Disciplinary PhD Scholarship in Mathematics and Statistics at the University of Melbourne, and by the Singapore Ministry of Education Academic Research Fund Tier 2 grant MOE2018-T2-2-076 at the National University of Singapore. A. Xia is supported by the Australian Research Council grants DP150101459 and DP190100613.
Competing interests
There were no competing interests to declare which arose during the preparation or publication process of this article.