Hostname: page-component-5b777bbd6c-pf7kn Total loading time: 0 Render date: 2025-06-26T00:28:52.688Z Has data issue: false hasContentIssue false
  • English
  • Français

On the last zero process with an application in corporate bankruptcy

Part of: Mathematical finance Stochastic processes Markov processes

Published online by Cambridge University Press:  28 May 2025

Erik J. Baurdoux  and
José M. Pedraza Open the ORCID record for José M. Pedraza [Opens in a new window]
Erik J. Baurdoux*
Affiliation:
London School of Economics and Political Science
José M. Pedraza*
Affiliation:
The University of Manchester
*
*Postal address: Houghton Street, London, WC2A 2AE, UK. Email: e.j.baurdoux@lse.ac.uk
**Postal address: Oxford Road, Manchester, M13 9PL, UK. Email: jose.pedrazaramirez@manchester.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

For a spectrally negative Lévy process X, consider 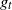$g_t$ and its infinitesimal generator. Moreover, with 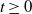$t\geq 0$, the last time X is below the level zero before time 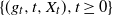$\{(g_t,t, X_t), t\geq 0 \}$ the length of a current positive excursion, we derive a general formula that allows us to calculate a functional of the whole path of 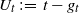$U_t\,:\!=\,t-g_t$. We use a perturbation method for Lévy processes to derive an Itô formula for the three-dimensional process 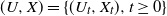$ (U, X)=\{(U_t, X_t),t\geq 0\}$ in terms of the positive and negative excursions of the process X. As a corollary, we find the joint Laplace transform of 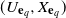$(U_{\mathbf{e}_q}, X_{\mathbf{e}_q})$, where 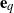$\mathbf{e}_q$ is an independent exponential time, and the q-potential measure of the process (U, X). Furthermore, using the results mentioned above, we find a solution to a general optimal stopping problem depending on (U, X) with an application in corporate bankruptcy. Lastly, we establish a link between the optimal prediction of 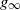$g_{\infty}$ and optimal stopping problems in terms of (U, X) as per Baurdoux, E. J. and Pedraza, J. M., 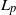$L_p$ optimal prediction of the last zero of a spectrally negative Lévy process, Annals of Applied Probability, 34 (2024), 1350–1402.

Keywords

Lévy processeslast zeropositive excursionsItô’s formulaoptimal stoppingcorporate bankruptcy

MSC classification

Primary: 60G40: Stopping times; optimal stopping problems; gambling theory 60G51: Processes with independent increments; L'evy processes
Secondary: 60J45: Probabilistic potential theory 91G50: Corporate finance
Type
Original Article
Information
Advances in Applied Probability , First View , pp. 1 - 48
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on behalf of Applied Probability Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Alili, L. and Kyprianou, A. E. (2005). Some remarks on first passage of Lévy processes, the American put and pasting principles. Ann. Appl. Probab. 15, 2062–2080.10.1214/105051605000000377CrossRefGoogle Scholar
Applebaum, D. (2009). Lévy Processes and Stochastic Calculus, 2nd edn. Cambridge Studies in Advanced Mathematics. Cambridge University Press.Google Scholar
Avram, F., Kyprianou, A. E. and Pistorius, M. R. (2004). Exit problems for spectrally negative Lévy processes and applications to (Canadized) Russian options. Ann. Appl. Probab. 14, 215–238.CrossRefGoogle Scholar
Azéma, J. and Yor, M. (1989). Étude d’une martingale remarquable. Séminaire de Probabilités de Strasbourg 23, 88–130.Google Scholar
Baurdoux, E. J. (2009). Last exit before an exponential time for spectrally negative Lévy processes. J. Appl. Probab. 46, 542–558.10.1239/jap/1245676105CrossRefGoogle Scholar
Baurdoux, E. J., Kyprianou, A. E. and Ott, C. (2016). Optimal prediction for positive self-similar Markov processes. Electron. J. Probab. 21, 24 pp.CrossRefGoogle Scholar
Baurdoux, E. J. and Pedraza, J. M. (2020). Predicting the last zero of a spectrally negative Lévy process. In XIII Symposium on Probability and Stochastic Processes. Springer, pp. 77–105.10.1007/978-3-030-57513-7_4CrossRefGoogle Scholar
Baurdoux, E. J. and Pedraza, J. M. (2024). $L_p$ optimal prediction of the last zero of a spectrally negative Lévy process. Ann, Appl, Probab, 34, 1350–1402.Google Scholar
Baurdoux, E. J. and Van Schaik, K. (2014). Predicting the time at which a Lévy process attains its ultimate supremum. Acta Appl. Math. 134, 21–44.CrossRefGoogle Scholar
Bertoin, J. (1998). Lévy Processes. Cambridge University Press.Google Scholar
Bichteler, K. (2002). Stochastic Integration with Jumps . Encyclopedia of Mathematics and its Applications. Cambridge University Press.Google Scholar
Bingham, N. H. (1975). Fluctuation theory in continuous time. Advances in Applied Probability 7, 705–766.CrossRefGoogle Scholar
Chan, T. (2004). Some applications of Lévy process in insurance and finance. Finance 25, 71–94.Google Scholar
Chiu, S. N. and Yin, C. (2005). Passage times for a spectrally negative Lévy process with applications to risk theory. Bernoulli 11, 511–522.Google Scholar
Cohen, S. N. and Elliott, R. J. (2015). Stochastic Calculus and Applications 2nd edn. Birkhäuser, New York.10.1007/978-1-4939-2867-5CrossRefGoogle Scholar
Cont, R. and Tankov, P. (2004). Financial modelling with jump processes. Chapman and Hall/CRC.Google Scholar
Dassios, A. and Wu, S. (2011). Double-barrier Parisian options. J. Appl. Probab. 48, 1–20.10.1239/jap/1300198132CrossRefGoogle Scholar
du Toit, J. and Peskir, G. (2008). Predicting the time of the ultimate maximum for Brownian motion with drift. In Mathematical Control Theory and Finance. Springer Berlin Heidelberg, pp. 95–112.10.1007/978-3-540-69532-5_6CrossRefGoogle Scholar
du Toit, J., Peskir, G. and Shiryaev, A. N. (2008). Predicting the last zero of Brownian motion with drift. Stochastics 80, 229–245.10.1080/17442500701840950CrossRefGoogle Scholar
Glover, K. and Hulley, H. (2014). Optimal prediction of the last-passage time of a transient diffusion. SIAM J. Control Optim. 52, 3833–3853.CrossRefGoogle Scholar
Glover, K., Hulley, H. and Peskir, G. (2013). Three-dimensional Brownian motion and the golden ratio rule. Ann. Appl. Probab. 23, 895–922.10.1214/12-AAP859CrossRefGoogle Scholar
Huzak, M., Perman, M., Šikić, H. and Vondraček, Z. (2004). Ruin probabilities and decompositions for general perturbed risk processes. Ann. Appl. Probab. 14, 1378–1397.10.1214/105051604000000332CrossRefGoogle Scholar
Huzak, M., Perman, M., Šikić, H. and Vondraček, Z. (2004). Ruin probabilities for competing claim processes. J. Appl. Probab. 41, 679–690.10.1239/jap/1091543418CrossRefGoogle Scholar
Jacka, S. D. (1991). Optimal stopping and the American put. Math. Finance 1, 1–14.CrossRefGoogle Scholar
Klüppelberg, C., Kyprianou, A. E. and Maller, R. A. (2004). Ruin probabilities and overshoots for general Lévy insurance risk processes. Ann. Appl. Probab. 14, 1766–1801.10.1214/105051604000000927CrossRefGoogle Scholar
Kyprianou, A., Kuznetsov, A. and Rivero, V. (2011). The theory of scale functions for spectrally negative Lévy processes. Lévy Matters. Lecture Notes in Mathematics. Springer.Google Scholar
Kyprianou, A., Schoutens, W. and Wilmott, P. (2006). Exotic Option Pricing and advanced Lévy Models. John Wiley & Sons.Google Scholar
Kyprianou, A. and Surya, B. (2005). On the Novikov-Shiryaev optimal stopping problems in continuous time. Electronic Commun. Probab. 10, 146–154.10.1214/ECP.v10-1144CrossRefGoogle Scholar
Kyprianou, A. E. (2014). Fluctuations of Lévy Processes with Applications. Springer Berlin Heidelberg.10.1007/978-3-642-37632-0CrossRefGoogle Scholar
Kyprianou, A. E. and Surya, B. A. (2007). A note on a change of variable formula with local time-space for Lévy processes of bounded variation. In Séminaire de Probabilités XL. Springer, pp. 97–104.CrossRefGoogle Scholar
Lamberton, D. and Mikou, M. (2008). The critical price for the American put in an exponential Lévy model. Finance Stoch. 12, 561–581.10.1007/s00780-008-0073-9CrossRefGoogle Scholar
Leland, H. E. (1994). Corporate debt value, bond covenants, and optimal capital structure. J. Finance 49, 1213–1252.CrossRefGoogle Scholar
Manso, G., Strulovici, B. and Tchistyi, A. (2010). Performance-sensitive debt. Rev. Financial Stud. 23, 1819–1854.10.1093/rfs/hhq005CrossRefGoogle Scholar
Mordecki, E. (1999). Optimal stopping for a diffusion with jumps. Finance Stoch. 3, 227–236.10.1007/s007800050060CrossRefGoogle Scholar
Mordecki, E. (2002). Optimal stopping and perpetual options for Lévy processes. Finance Stoch. 6, 473–493.10.1007/s007800200070CrossRefGoogle Scholar
Paroissin, C. and Rabehasaina, L. (2013). First and last passage times of spectrally positive Lévy processes with application to reliability. Methodol. Comput. Appl. Probab. 17, 351–372.10.1007/s11009-013-9360-9CrossRefGoogle Scholar
Peskir, G. (2007). A change-of-variable formula with local time on surfaces. In Séminaire de Probabilités XL. Springer, pp. 70–96.CrossRefGoogle Scholar
Peskir, G. and Shiryaev, A. (2006). Optimal stopping and free-boundary problems. Birkhäuser Basel.Google Scholar
Protter, P. E. (2005). Stochastic Integration and Differential Equations. Springer Berlin Heidelberg.10.1007/978-3-662-10061-5CrossRefGoogle Scholar
Quah, J. K.-H. and Strulovici, B. (2013). Discounting, values, and decisions. J. Pol. Econom. 121, 896–939.CrossRefGoogle Scholar
Revuz, D. and Yor, M. (1999). Continuous Martingales and Brownian motion. Springer Berlin Heidelberg.10.1007/978-3-662-06400-9CrossRefGoogle Scholar
Salminen, P. (1988). On the first hitting time and the last exit time for a Brownian motion to/from a moving boundary. Adv. Appl. Probab. 20, 411–426.10.2307/1427397CrossRefGoogle Scholar
Sato, K.-i. (1999). Lévy processes and Infinitely Divisible Distributions. Cambridge University Press.Google Scholar
Schoutens, W. (2003). Lévy Processes in Finance: Pricing Financial Derivatives. Wiley Online Library.CrossRefGoogle Scholar
Shiryaev, A. N. (2009). On conditional-extremal problems of the quickest detection of nonpredictable times of the observable Brownian motion. Theory Probab. Appl. 53, 663–678.10.1137/S0040585X97983882CrossRefGoogle Scholar