Hostname: page-component-76fb5796d-skm99 Total loading time: 0 Render date: 2024-04-27T09:04:32.978Z Has data issue: false hasContentIssue false
  • English
  • Français

Strong convergence of an epidemic model with mixing groups

Part of: Limit theorems Markov processes

Published online by Cambridge University Press:  01 September 2023

Frank Ball Open the ORCID record for Frank Ball [Opens in a new window]  and
Peter Neal Open the ORCID record for Peter Neal [Opens in a new window]
Frank Ball*
Affiliation:
University of Nottingham
Peter Neal*
Affiliation:
University of Nottingham
*
*Postal address: School of Mathematical Sciences, University of Nottingham, NG7 2RD, United Kingdom.
*Postal address: School of Mathematical Sciences, University of Nottingham, NG7 2RD, United Kingdom.
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider an SIR (susceptible 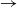$\to$ infective 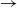$\to$ recovered) epidemic in a closed population of size n, in which infection spreads via mixing events, comprising individuals chosen uniformly at random from the population, which occur at the points of a Poisson process. This contrasts sharply with most epidemic models, in which infection is spread purely by pairwise interaction. A sequence of epidemic processes, indexed by n, and an approximating branching process are constructed on a common probability space via embedded random walks. We show that under suitable conditions the process of infectives in the epidemic process converges almost surely to the branching process. This leads to a threshold theorem for the epidemic process, where a major outbreak is defined as one that infects at least 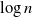$\log n$ individuals. We show further that there exists 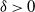$\delta \gt 0$, depending on the model parameters, such that the probability that a major outbreak has size at least 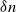$\delta n$ tends to one as 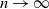$n \to \infty$.

Keywords

Branching processcouplingrandom walkSIR epidemicsize of epidemicthreshold theorem

MSC classification

Primary: 92D30: Epidemiology 60F15: Strong theorems
Secondary: 60J27: Continuous-time Markov processes on discrete state spaces 60J80: Branching processes (Galton-Watson, birth-and-death, etc.)
Type
Original Article
Information
Advances in Applied Probability , First View , pp. 1 - 34
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of Applied Probability Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bailey, N. T. J. (1975). The Mathematical Theory of Infectious Diseases and Its Applications, 2nd edn. Griffin, London.Google Scholar
Ball, F. (1983). The threshold behaviour of epidemic models. J. Appl. Prob. 20, 227–241.CrossRefGoogle Scholar
Ball, F. and Donnelly, P. (1995). Strong approximations for epidemic models. Stoch. Process. Appl. 55, 1–21.CrossRefGoogle Scholar
Ball, F. and Neal, P. (2017). The asymptotic variance of the giant component of configuration model random graphs. Ann. Appl. Prob. 27, 1057–1092.CrossRefGoogle Scholar
Ball, F. and Neal, P. (2022). An epidemic model with short-lived mixing groups. J. Math. Biol. 85, article no. 63.CrossRefGoogle Scholar
Ball, F. and O’Neill, P. (1994). Strong convergence of stochastic epidemics. Adv. Appl. Prob. 26, 629–655.CrossRefGoogle Scholar
Bartlett, M. S. (1955). An Introduction to Stochastic Processes. Cambridge University Press.Google Scholar
Cortez, R. (2022). SIR model with social gatherings. Preprint. Available at https://arxiv.org/abs/2203.08260.Google Scholar
Durrett, R. (2010). Probability: Theory and Examples. Cambridge University Press.CrossRefGoogle Scholar
Ethier, S. N. and Kurtz, T. G. (1986). Markov Processes: Characterization and Convergence. John Wiley, Hoboken, NJ.CrossRefGoogle Scholar
Jagers, P. (1975). Branching Processes with Biological Applications. John Wiley, London.Google Scholar
Kendall, D. (1956). Deterministic and stochastic epidemics in closed populations. In Proc. 3rd Berkeley Symp. Math. Statist. Prob., Vol. IV, University of California Press, Berkeley, pp. 149–165.CrossRefGoogle Scholar
Metz, J. A. J. (1978). The epidemic in a closed population with all susceptibles equally vulnerable; some results for large susceptible populations and small initial infections. Acta Biotheoretica 27, 75–123.CrossRefGoogle Scholar
Nerman, O. (1981). On the Convergence of Supercritical General (C-M-J) Branching Processes. Z. Wahrscheinlichkeitsth. 57, 365–395.CrossRefGoogle Scholar
Newman, M. E. J. (2002). Spread of epidemic disease on networks. Phys. Rev. E 66, article no. 016128.CrossRefGoogle ScholarPubMed
Pollett, P. K. (1990). On a model for interference between searching insect parasites. J. Austral. Math. Soc. B 32, 133–150.CrossRefGoogle Scholar
Whittle, P. (1955). The outcome of a stochastic epidemic—a note on Bailey’s paper. Biometrika 42, 116–122.Google Scholar
Williams, T. (1971). An algebraic proof of the threshold theorem for the general stochastic epidemic. Adv. Appl. Prob. 3, 223.CrossRefGoogle Scholar