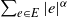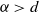Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Hirsch, Christian
and
Willhalm, Daniel
2024.
Lower large deviations for geometric functionals in sparse, critical and dense regimes
.
Latin American Journal of Probability and Mathematical Statistics,
Vol. 21,
Issue. 2,
p.
923.