Low physical activity (PA) levels in daily life are probably correlated with obesity and other diseases(1). According to the International Association for the Study of Obesity, prevention of weight regain in formerly obese individuals requires 60–90 min of daily moderate activity or lesser amounts of vigorous activity, with 45–60 min of daily moderate activity required to prevent the transition to overweight or obese(Reference Saris, Blair and van Baak2). In addition to exercise, non-exercise activity thermogenesis, a much larger part of daily PA, may also contribute to obesity prevention(Reference Levine, Eberhardt and Jensen3, Reference Levine, Lanningham-Foster and McCrady4). Therefore, assessment of the type, quantity and intensity of PA is important for the development of strategies to prevent obesity and chronic diseases. However, accurate methods for the measurement of energy expenditures (EE) induced by various PA under free-living conditions are still under consideration.
At present, several methods are used for the measurement of EE in a field setting(Reference Dale, Welk, Matthews and Welk5, Reference Melanson and Freedson6). The doubly labelled water method displays high accuracy for the measurement of 24 h EE under free-living conditions. However, this method can only evaluate total EE and cannot provide day-to-day or minute-by-minute variations. Although questionnaires could individually measure PA intensity and EE (as value by intensity × time) in addition to the PA type, the accuracy of these methods is not sufficient(Reference Neilson, Robson and Friedenreich7). On the other hand, accelerometers are objective, small, non-invasive tools for measuring PA intensity and EE, with the potential to measure locomotive as well as household activities(Reference Chen and Bassett8–Reference Ward, Evenson and Vaughn10). Furthermore, activity monitors such as accelerometers or pedometers may serve as useful tools for promoting active life behaviour(Reference Richardson, Newton and Abraham11, Reference Bravata, Smith-Spangler and Sundaram12).
At the least, uniaxial and triaxial accelerometers can accurately estimate the intensity of ambulatory activities(Reference Bassett, Ainsworth and Swartz13–Reference Welk, Blair and Wood15). However, the intensities of household activities such as vacuuming and sweeping cannot be accurately estimated by accelerometers, possibly leading to underestimation of total EE by algorithms based on locomotive activities(Reference Matthews14). Indeed, different relationships between counts per minute and metabolic equivalents (MET) observed for locomotive v. household activities led to MET underestimation for household activities(Reference Bassett, Ainsworth and Swartz13–Reference Welk, Blair and Wood15). Time spent in sedentary and light activities is also underestimated by locomotion-based equations(Reference Rothney, Schaefer and Neumann16). Therefore, accurate MET estimation for household and sedentary activities is required in addition to locomotive activity.
Recently, several studies have attempted to discriminate between PA types using accelerometer counts(Reference Chen and Sun17–Reference Zhang, Werner and Sun26). Although these algorithms have improved accuracy for estimating the MET of various activities compared with single regression models, some limitations remain: percentage of correct classification was slightly lower in some types of PA(Reference Crouter, Clowers and Bassett21, Reference Midorikawa, Tanaka and Kaneko22); multiple sensors make it difficult to continuously wear the device on the body(Reference Zhang, Werner and Sun26); estimation is a complex procedure requiring large amounts of data, a barrier for applied researchers as well as for the general public. An accelerometer-based algorithm that accurately and immediately estimates PA intensity would be a useful tool for assessing PA in free-living conditions, as well as for promoting active life behaviour in general users. We have recently developed a simple but accurate algorithm for the classification of locomotive and household activities, using the ratio of unfiltered to filtered synthetic acceleration (ACCunfil/ACCfil) combined with a gravity-removal PA classification algorithm (GRPACA)(Reference Oshima, Kawaguchi and Tanaka27). A correct classification percentage of almost 100 % was achieved during our selected activities. Furthermore, we have confirmed the separation of sedentary activities from both locomotive and household activities by accelerometer counts. Therefore, the purpose of the present study was to develop a new model for instantly estimating the intensity of daily PA using a triaxial accelerometer.
Subjects and methods
Subjects
A total of sixty-six subjects (thirty-one males and thirty-five females) volunteered to participate in the present study. The present study was conducted according to the guidelines laid down in the Declaration of Helsinki, and all procedures involving human subjects were approved by the Ethical Committee of the National Institute of Health and Nutrition in Tokyo, Japan. Subjects were excluded from the study if they had any contraindications to exercise, or if they were physically unable to complete the activities. Descriptive characteristics of the study subjects are presented in Table 1. Subjects were randomly assigned into validation (n 44) and cross-validation (n 22) groups. Before measurement, the purpose and procedure of the study were explained in detail. Informed consent was signed by all subjects.
Table 1 Physical characteristics of the subjects in each group
(Mean values and standard deviations)

* Subjects were randomly assigned into validation (67 %) and cross-validation (33 %) groups matched for age, height and weight.
Anthropometric measurements
Before performing PA, body weight was measured by a digital scale to the nearest 0·1 kg, with the subjects dressed in light clothing. Barefoot standing height was measured to the nearest 0·1 cm using a wall-mounted stadiometer (YL-65S; Yagami, Nagoya, Japan). BMI was calculated as body weight (kg) divided by height squared (m2).
Experimental protocol
Fasting subjects visited the laboratory in the morning of the experimental day. After anthropometric measurements, they performed fourteen activities with a facemask and Douglas bag while wearing a triaxial accelerometer on the left side of the waist. The selected activities were as follows: (1) sedentary activity – resting in the supine position as BMR, resting in the sitting position as RMR and personal computer work; (2) household activity – laundry, dishwashing, moving a small load (5 kg) and vacuuming; (3) locomotive activity – slow walking (3·3 km/h), normal walking (4·2 km/h), brisk walking (6·0 km/h), normal walking while carrying a bag (3 kg) in the hand, jogging (8·4 km/h) on a track, and ascending and descending stairs at personal normal speeds without using handrails. These activities were chosen as representative activities of daily life, based on our observations in a preliminary study using the activity records of other subjects. The subjects were permitted to consume only drinking-water during the experiment. They were instructed to lie down quietly for 30 min, and then BMR was measured for two periods of 10 min, followed by RMR measurement for 10 min. Subsequently, the other activities were performed for 3–7 min. The entire experimental protocol took each subject about 4·5 h to complete, and there was enough rest between activities to eliminate any carry-over effect from one activity to another. Each subject performed the experiment following the same schedule. The expired air for the subject in each activity was collected under a steady state. We defined the beginning of the steady state as 2–3 min after starting an activity, depending on the activity intensity(Reference Ohkawara, Tanaka and Ishikawa-Takata28). This experimental protocol has previously been described in detail(Reference Oshima, Kawaguchi and Tanaka27).
Indirect calorimetry
During each activity, the subject's expired air was collected in a Douglas bag. Expired O2 and CO2 gas concentrations were measured by MS (ARCO-1000; Arco System, Kashiwa, Japan), and gas volume was determined using a certified dry gas meter (DC-5; Shinagawa, Tokyo, Japan). For each measurement, the gas analyser was initially calibrated using a certified gas mixture and atmospheric air. EE was estimated from VO2 and VCO2 using Weir's equation(Reference Weir29). MET values as reference were calculated as EE during the activities divided by the measured RMR.
Triaxial accelerometer
We used a triaxial accelerometer with 4 GB of memory consisting of Micro Electro Mechanical Systems-based accelerometers (LIS3LV02DQ; ST-Microelectronics, Geneva, Switzerland), which respond to both acceleration due to movement and gravitational acceleration. The sensor was built into a plastic case without a liquid crystal display and was designed to be clipped to a waist belt (size: 80 × 50 × 20 mm; weight: approximately 60 g including batteries). Anteroposterior (x-axis), mediolateral (y-axis) and vertical (z-axis) acceleration measurements were obtained during each activity at a rate of 32 Hz to 12 bit accuracy. The range of the acceleration data of each axis is ± 6 G, resulting in a resolution of 3 mG. The acceleration data were uploaded to a personal computer.
The signals obtained from the triaxial accelerometer were processed in the following way. Each of the three signals from the triaxial accelerometer was passed through a high-pass filter with a cut-off frequency of 0·7 Hz, in order to remove the gravitational acceleration component from the signal. We calculated the synthetic acceleration of all three axes (vector magnitude ![]() ) using signals before and after high-pass filtering. Then, the ratio of ACCunfil to ACCfil was calculated. The acceleration signals, calculated as the average of the absolute value of the accelerometer output of each axis from 10 s epochs at the middle of each activity, were processed to various acceleration output variables. In our previous study, we reported the algorithm for the classification of household and locomotive activities by the ACCunfil:ACCfil ratio which resulted in almost 100 % correct demarcation for our eleven selected activities(Reference Oshima, Kawaguchi and Tanaka27).
) using signals before and after high-pass filtering. Then, the ratio of ACCunfil to ACCfil was calculated. The acceleration signals, calculated as the average of the absolute value of the accelerometer output of each axis from 10 s epochs at the middle of each activity, were processed to various acceleration output variables. In our previous study, we reported the algorithm for the classification of household and locomotive activities by the ACCunfil:ACCfil ratio which resulted in almost 100 % correct demarcation for our eleven selected activities(Reference Oshima, Kawaguchi and Tanaka27).
A commercial product (Activity Style Pro HJA-350IT; Omron Healthcare, Kyoto, Japan) has been developed from the prototype accelerometer that we made in the present study. This commercial device measures 74 × 46 × 34 mm and weighs 60 g, including batteries. The liquid crystal display in this device has several modes that provide different types of information: (1) a research mode that provides no information; (2) a mode that displays step counts; (3) a mode that displays real-time MET intensity. Both devices are shown in Fig. 1.

Fig. 1 Prototype accelerometer used in the present study and a commercial accelerometer based on the algorithm developed in the present study. (a) Prototype accelerometer that was used to perform all measurements; (b) subjects wore the prototype accelerometer on the waist with a clip during the entire protocol; (c) commercial accelerometer based on the algorithm that was developed in the present study; (d) real-time metabolic equivalents (MET) are shown on the liquid crystal display (LCD) of the commercial accelerometer (the LCD can also show step counts).
Statistical analysis
All values are presented as means and standard deviations. Differences are considered to be statistically significant if the P value is less than 0·05. The relationship between measured MET and the ACCfil count in the validation group was evaluated by Pearson's correlation coefficient (r) and the standard error of the estimate. Linear and non-linear regression models were used in the validation group to develop equations to predict MET based on the intensity of PA, as measured by the ACCfil count. Differences between measured and estimated MET in the cross-validation group were assessed by one-way ANOVA followed by Dunnett's post hoc test or a paired t test. Bland–Altman plots were used to graphically show the variability in individual error scores in the cross-validation group(Reference Bland and Altman30). All statistical analyses were performed using SPSS version 15.0J for Windows (SPSS, Inc., Chicago, IL, USA).
Results
Data collected during the present study were analysed if both MET and ACC could be correctly measured during each activity. Mean EE, MET, ACCunfil, ACCfil and the ACCunfil:ACCfil ratio for each activity are shown in Table 2. As suggested previously(Reference Rothney, Schaefer and Neumann16), the one-regression models overestimate MET for light activity; we observed a similar result (data not shown). Therefore, we modelled the classification of our selected activities into three types of activities: sedentary, household and locomotive (Fig. 2). Sedentary activities are discriminated from household and locomotive activities, because ACCfil for sedentary activities was lower than for other activities. Household and locomotive activities are classified by the ACCunfil:ACCfil ratio according to our previous study (1·16)(Reference Oshima, Kawaguchi and Tanaka27).
Table 2 Energy expenditure, metabolic equivalents (MET), accelerations and acceleration ratios for each activity in the validation group
(Mean values and standard deviations, n 44)

* MET were calculated as energy expenditure for each activity divided by energy expenditure for resting in the sitting position.
† MET were calculated as energy expenditure for each activity divided by 4·184 kJ/kg per h.
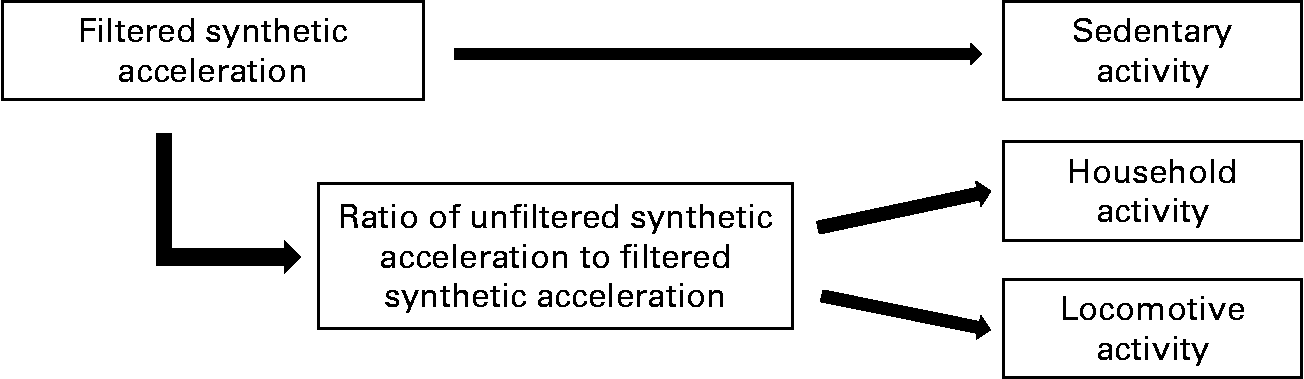
Fig. 2 Algorithm for the classification of three different activity types, using a triaxial accelerometer.
Fig. 3 depicts the relationship between measured MET and ACCfil during household and locomotive activities performed by the validation group. The correlation coefficients for locomotive (r 0·961, P < 0·001), household (r 0·907, P < 0·001) and combined household and locomotive activities (r 0·930, P < 0·001) were high. We developed linear and non-linear regressions for estimating the intensities of household and locomotive activities; ascending and descending stairs were excluded from developing regressions, because the relationships between MET and ACCfil for ascending and descending stairs differed from the relationship for the other locomotive activities (Table 3). As a result, the linear regression calculated with combined data of household and locomotive activities had a lower r value compared with all other regressions for locomotive activities only. Regressions for only household activities had slightly lower r values than those for all activities, but the regression standard errors of estimate were improved. Table 4 shows the cross-validation for all regressions. Significant differences were observed between measured values and values estimated from model 1 for most activities. However, models 2–5 accurately estimated the intensity of most household and locomotive activities, with the exceptions of ascending and descending stairs from models 2–5 and normal walking from models 2, 4 and 5, although the differences for normal walking were relatively small. In the cross-validation group, household and locomotive activities were correctly classified 100 % of the time by the ACCunfil:ACCfil threshold reported previously(Reference Oshima, Kawaguchi and Tanaka27). Bland–Altman plots showed that there was improved accuracy of individual activities with models 2–5 compared with model 1 (Fig. 4). Although all models tended to underestimate higher vigorous intensity activity with significant r 2 values (P < 0·05), household activities were clearly well estimated by models 2–5. The results of the present study remained consistent, whether estimated from linear or non-linear regressions or from sex-specific regressions.

Fig. 3 Relationships between measured metabolic equivalents (MET) and filtered synthetic accelerations during locomotive and household activities in the validation group (n 44). R 1 (r 0·907, P < 0·001), regression line for household activities only; R 2 (r 0·930, P < 0·001), regression line for combined household and locomotive activities; R 3 (r 0·961, P < 0·001), regression line for locomotive activity only. Ascending and descending stairs were removed from the regression analyses for R 1, R 2 and R 3. ![]() , Laundry;
, Laundry; ![]() , dishwashing;
, dishwashing; ![]() , moving a small load;
, moving a small load; ![]() , vacuuming;
, vacuuming; ![]() , slow walking;
, slow walking; ![]() , normal walking;
, normal walking; ![]() , brisk walking;
, brisk walking; ![]() , walking while carrying a bag;
, walking while carrying a bag; ![]() , jogging;
, jogging; ![]() , ascending stairs;
, ascending stairs; ![]() , descending stairs.
, descending stairs.
Table 3 Equations for estimating metabolic equivalents (MET) in locomotive and household activities by using filtered synthetic acceleration (ACCfil, mG) in the validation group (n 44)
(r Values and standard errors of the estimate (SEE))

* P < 0·001.
Table 4 Absolute and percentage of differences between measured and estimated metabolic equivalents (MET) from five equation models for household and locomotive activities in the cross-validation group
(Mean values and standard deviations, n 22)

Mean values were significantly different compared with measured MET: *P < 0·05, **P < 0·01, ***P < 0·001.
† Linear regression model for estimating locomotive and household activities together.
‡ Linear regression model for estimating locomotive and household activities separately.
§ Non-linear regression model for estimating locomotive and household activities separately.
∥ Sex-specific linear regression model for estimating locomotive and household activities separately.
¶ Sex-specific non-linear regression model for estimating locomotive and household activities separately.

Fig. 4 Bland–Altman analysis. Differences between measured and estimated metabolic equivalents (MET) are plotted against measured and estimated mean MET for household and locomotive activities. (a) Model 1, linear regression model for estimating locomotive and household activities together (r 0·237); (b) model 2, linear regression model for estimating locomotive and household activities separately (r 0·207); (c) model 3, non-linear regression model for estimating locomotive and household activities separately (r 0·219); (d) model 4, sex-specific linear regression model for estimating locomotive and household activities separately (r 0·212); (e) model 5, sex-specific non-linear regression model for estimating locomotive and household activities separately (r 0·207). —, Mean; - - -, 95 % CI of the observations.
Fig. 5 depicts the relationship between measured MET and ACCfil during sedentary activities performed by the validation group. We selected three activities to represent sedentary activities. As shown in Fig. 5, we calculated the regression equation for estimating the intensity of sedentary activities by including dishwashing with the lowest MET on average in our selected household and locomotive activities. The threshold for the classification between sedentary activities and other activities was determined by the point of intersection in the linear regressions for sedentary activities and household activities (29·9 mG). With these threshold and regression equations, resting in the supine position (mean difference 0·04 (sd 0·06) MET, P < 0·01), personal computer work (mean difference − 0·03 (sd 0·09) MET, NS) and dishwashing (mean difference 0·02 (sd 0·31) MET, NS) were estimated adequately in the cross-validation group.

Fig. 5 Relationship between measured metabolic equivalents (MET) and filtered synthetic accelerations during sedentary activities in the validation group (n 44). E 1 (r 0·942, P < 0·001, standard error of estimate 0·151 MET), regression line for sedentary activities; E 2, regression line for household activities. * Threshold point for the classification between sedentary and household activities (29·9 mG). Dishwashing was included in both E 1 and E 2. ○, Resting in the supine position; ×, personal computer work; △, dishwashing.
Final model for estimating intensity of physical activity (n 66)
Sedentary activity:MET = 0·8823+0·0351 × ACCfil.
Discussion
We have developed a new model to estimate the intensity of daily PA, using a triaxial accelerometer in combination with a novel PA classification algorithm. We classified PA into locomotive, household and sedentary activities with thresholds determined by the ACCunfil:ACCfil ratio (GRPACA) or accelerometer counts(Reference Oshima, Kawaguchi and Tanaka27). The rate of correct classification was excellent: 100 % of the activities performed by our subjects were correctly classified as locomotive or household. With our new classification algorithm, the regressions clearly improved the accuracy of estimating the intensity of various PA, compared with a non-classification model. This novel method is capable of estimating the intensity of PA accurately and immediately, serving as a practical field tool for researchers as well as for general users.
In agreement with previous studies(Reference Crouter and Bassett18–Reference Crouter, Clowers and Bassett21, Reference Corder, Brage and Mattocks31), we observed that the multiple equation model improved the accuracy of estimating household and locomotive activity intensities, compared with the one-equation model; accuracy improvements occurred for household activities in particular. With the exceptions of ascending and descending stairs, average percentage differences were within 10 % in the two-equation model, with more than 10 % differences in several activities in the one-equation model. Furthermore, we attempted to estimate the intensity of PA with non-linear regression and sex-specific regression (or non-regression) models. Prediction errors obtained from the linear and non-linear regression models were comparable in the present study (Table 4). While it is still controversial whether the linear or non-linear regression model is a better predictive model(Reference Chen and Bassett8), inclusion of the GRPACA did not necessitate non-linear or sex-specific regression equations. To our knowledge, there is no evidence of a quadratic relationship between MET and accelerometer counts in various PA. Therefore, the linear regression model may obtain comparable predictions as the non-linear regression model in the present study, under actual free-living conditions. Furthermore, the sex-specific equation model did not provide a more accurate estimation (Table 4), indicating that we have developed new equations by linear regressions without taking sex into account.
Accurate estimation of sedentary activities is important, as many people perform sedentary activities at least several hours/d(32, Reference Westerterp33). Previously developed accelerometer-based models overestimate the intensity of sedentary activities(Reference Rothney, Schaefer and Neumann16). In the present study, sedentary activities clearly had lower accelerometer counts than other activities. Initially, we hypothesised that the cut-off threshold between intensities of sedentary and other activities should be the midpoint of the highest sedentary accelerometer count and the lowest accelerometer count from the other activities. However, in the present study, we observed a small gap between sedentary and household activities in the relationship between MET and ACCfil. Therefore, we developed the equation for sedentary activities by including dishwashing, which displayed the lowest accelerometer counts of our household or locomotive activity. Using this consideration, activities about 1·5 MET could be estimated accurately. Therefore, we have classified an activity of less than 2 MET as a sedentary activity, using a cut-off threshold determined by accelerometer counts.
Although PA intensity estimates were improved with our model, we could not directly compare the present results with previously reported models designed for data collecting and developing equations. However, our accuracies for some activities, such as personal computer work, vacuuming and dishwashing, are slightly better than the results obtained by Crouter et al. (Reference Crouter and Bassett18–Reference Crouter, Clowers and Bassett21, Reference Crouter, Kuffel and Haas34), who used two equations with a classification algorithm based on the CV of the acceleration count. Moreover, our model possesses the following advantages over previous models: (1) our classification algorithm is accurate but simple, leading to immediate estimation of PA intensity following a long period of data collection; (2) our measuring device is secured to the waist by a clip only; (3) the Douglas bag method, not a portable analyser, was used as the reference method; (4) MET were calculated with measured RMR (not 3·5 ml/kg per min or 4·2 kJ/kg per h (1 kcal/kg per h)); (5) values from a triaxial accelerometer, not a uniaxial accelerometer, were used for developing equations.
Several algorithms have been developed for PA classification. These algorithms were constructed using the CV of the acceleration count based on the ActiGraph or Actical devices(Reference Crouter and Bassett18–Reference Crouter, Clowers and Bassett21, Reference Crouter, Kuffel and Haas34) or using the ratio of vertical acceleration counts to horizontal acceleration counts based on the ActivTracer device(Reference Midorikawa, Tanaka and Kaneko22, Reference Tanaka, Tanaka and Kawahara25). In these studies, the percentage of correct classifications does not seem to be high, even for the subjects used in the classification development. Our algorithm may classify locomotive and household activities with higher accuracy. On the other hand, other reported classification algorithms(Reference Zhang, Werner and Sun26, Reference Bonomi, Plasqui and Goris35, Reference Staudenmayer, Pober and Crouter36) were developed to divide PA into further subtypes. These additional divisions require a large quantity of data, a complex calculation process or the placement of sensors over the whole body; it is difficult to maintain battery power over long periods, to check PA intensities in real time and to wear and remove the device easily. Our device is worn just on the waist, is held by a clip and PA intensities were displayed immediately. This unique device is useful for applied researchers or professional health advisers to investigate PA in the field, and general users can monitor their activity status by themselves, as the commercial product has an liquid crystal display that can indicate real-time MET values or step counts.
We employed the Douglas bag method as a reference for measuring EE, while previous studies used a portable metabolic system such as Aerosport TEEM 100 or COSMED K4b2. For these portable metabolic systems, validation of assessing EE during PA has been reported(Reference Maiolo, Melchiorri and Iacopino37–Reference Wideman, Stoudemire and Pass40). A portable metabolic system also has the advantage of measuring various dynamic activities outdoors. However, portable metabolic systems slightly overestimate or underestimate O2 uptake during exercise testing, compared with reference methods(Reference Wideman, Stoudemire and Pass40–Reference Mc Naughton, Sherman and Roberts43). Therefore, the Douglas bag method may be preferable to a portable metabolic system as a reference method for measuring EE during various types of PA.
Whether measured values or a constant value of 3·5 ml/kg should be used for the RMR value of 1 MET is debatable. Typical values for the normal-weight population were 3·5 ml/kg per min and 4·2 kJ/kg per h (1 kcal/kg per h). However, average measured RMR were much lower than 3·5 ml/kg per min or 4·2 kJ/kg per h (1 kcal/kg per h) in 671 subjects, although many were overweight or obese(Reference Byrne, Hills and Hunter44). In particular, body composition contributed to the variance in RMR. In the present study, the average RMR value was 4·1 kJ/kg per h (0·99 kcal/kg per h), but the standard deviation was relatively large (0·8 kJ/kg per h (0·19 kcal/kg per h)). To our knowledge, no description exists of whether the RMR value of 3·5 ml/kg per min was previously measured in a fasting state(Reference Jette, Sidney and Blumchen45), although the present study and Byrne et al. (Reference Byrne, Hills and Hunter44) measured RMR in the fasting state. Therefore, the use of measured RMR as 1 MET could lead to increased accuracy of estimating the intensity of PA.
A triaxial accelerometer, capable of measuring both vertical and horizontal accelerations, is more informative than a uniaxial accelerometer, possibly permitting more accurate estimates of PA intensities. However, previous studies(Reference Rothney, Schaefer and Neumann16, Reference Tanaka, Tanaka and Kawahara25, Reference Leenders, Sherman and Nagaraja46) have reported that the accuracy of estimating PA intensities did not differ between triaxial and uniaxial accelerometers if these values were estimated by a one-equation model. Although our classification algorithm can calculate the cut-off threshold even using a uniaxial accelerometer count, we confirmed that the classification developed with a synthetic accelerometer count is more accurate than that based only on a vertical (uniaxial) accelerometer count. Therefore, our estimation by triaxial accelerometer counts should lead to increased accuracy compared with a uniaxial accelerometer.
The present study had several limitations. We could not accurately estimate the intensity of ascending and descending stairs. Although previous studies(Reference Crouter and Bassett18–Reference Crouter, Clowers and Bassett21, Reference Staudenmayer, Pober and Crouter36) have estimated the intensities of these activities relatively well, validity was assessed by a condition combining ascension and descension of stairs, with only Yamazaki et al. (Reference Yamazaki, Gen-No and Kamijo47) performing the individual assessments. Under daily living conditions, ascending and descending stairs are normally performed separately, and thus these activities should be assessed separately. In addition, we did not include stationary ergometer or cycling in the present study. Furthermore, the developed model tended to underestimate higher vigorous intensity activity. Therefore, future studies are needed using the doubly labelled water method or a metabolic chamber to investigate the validity of our model. In addition, studies are needed to compare our accelerometer with other types of accelerometers under free-living conditions. Furthermore, more investigation is needed to determine how well the model developed in the present study applies to other populations such as obese individuals or children.
We have recently reported a simple but accurate classification algorithm to differentiate between locomotive and household activities, with a cut-off determined by the ACCunfil:ACCfil ratio(Reference Oshima, Kawaguchi and Tanaka27). Additionally, sedentary activities could be discriminated from household and locomotive activities with accelerometer counts. With this classification algorithm, our new model exhibited improved accuracy in estimating the intensity of various PA, compared with non-classification models. Furthermore, this new model is capable of estimating PA intensity immediately. Therefore, the method is useful for field investigations by scientists as well as for self-monitoring of activity by the general public.
Acknowledgements
The present study was supported by the Health and Labor Sciences Research Grants for Comprehensive Research on Cardiovascular and Life-Style Related Diseases from the Japanese Ministry of Health, Labor and Welfare (principal investigator: S. T.). Heartfelt thanks are due to the subjects who participated in the present study. We wish to thank the members of the National Institute of Health and Nutrition and Omron Healthcare Company Limited, especially Hiroko Kogure, Emiko Taguri, Rieko Miyake, Ryosuke Doi and Kaori Kawaguchi for their help in data acquisition and analysis. K. O., S. T., Y. O., Y. H., K. I.-T. and I. T. designed the study; K. O., S. T., Y. O., Y. H. and K. I.-T. performed the experiments; K. O., S. T. and Y. O. analysed the data; K. O., S. T. and Y. O. wrote a draft of the manuscript; Y. H., K. I.-T. and I. T. reviewed and edited the manuscript. None of the authors had a conflict of interest.










