Article contents
GÖDEL DIFFEOMORPHISMS
Published online by Cambridge University Press: 01 September 2020
Abstract
In 1932, von Neumann proposed classifying the statistical behavior of differentiable systems. Joint work of B. Weiss and the author proved that the classification problem is complete analytic. Based on techniques in that proof, one is able to show that the collection of recursive diffeomorphisms of the 2-torus that are isomorphic to their inverses is 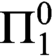 $\Pi ^0_1$-hard via a computable 1-1 reduction. As a corollary there is a diffeomorphism that is isomorphic to its inverse if and only if the Riemann Hypothesis holds, a different one that is isomorphic to its inverse if and only if Goldbach’s conjecture holds and so forth. Applying the reduction to the
$\Pi ^0_1$-hard via a computable 1-1 reduction. As a corollary there is a diffeomorphism that is isomorphic to its inverse if and only if the Riemann Hypothesis holds, a different one that is isomorphic to its inverse if and only if Goldbach’s conjecture holds and so forth. Applying the reduction to the 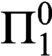 $\Pi ^0_1$-sentence expressing “ZFC is consistent” gives a diffeomorphism T of the 2-torus such that the question of whether
$\Pi ^0_1$-sentence expressing “ZFC is consistent” gives a diffeomorphism T of the 2-torus such that the question of whether 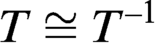 $T\cong T^{-1}$ is independent of ZFC.
$T\cong T^{-1}$ is independent of ZFC.
MSC classification
Information
- Type
- Articles
- Information
- Copyright
- © The Association for Symbolic Logic 2020
References
REFERENCES
- 1
- Cited by


