Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-23T15:03:37.098Z Has data issue: false hasContentIssue false
  • English
  • Français

A SPARSITY RESULT FOR THE DYNAMICAL MORDELL–LANG CONJECTURE IN POSITIVE CHARACTERISTIC

Part of: Arithmetic and non-Archimedean dynamical systems Arithmetic algebraic geometry Sequences and sets

Published online by Cambridge University Press:  23 February 2021

DRAGOS GHIOCA Open the ORCID record for DRAGOS GHIOCA [Opens in a new window] ,
ALINA OSTAFE Open the ORCID record for ALINA OSTAFE [Opens in a new window] ,
SINA SALEH Open the ORCID record for SINA SALEH [Opens in a new window]  and
IGOR E. SHPARLINSKI Open the ORCID record for IGOR E. SHPARLINSKI [Opens in a new window]
DRAGOS GHIOCA*
Affiliation:
Department of Mathematics, University of British Columbia, Vancouver, BCV6T 1Z2, Canada
ALINA OSTAFE
Affiliation:
School of Mathematics and Statistics, University of New South Wales, Sydney, NSW2052, Australia e-mail: alina.ostafe@unsw.edu.au
SINA SALEH
Affiliation:
Department of Mathematics, University of British Columbia, Vancouver, BCV6T 1Z2, Canada e-mail: sinas@math.ubc.ca
IGOR E. SHPARLINSKI
Affiliation:
School of Mathematics and Statistics, University of New South Wales, Sydney, NSW2052, Australia e-mail: igor.shparlinski@unsw.edu.au
*
e-mail: dghioca@math.ubc.ca
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove a quantitative partial result in support of the dynamical Mordell–Lang conjecture (also known as the DML conjecture) in positive characteristic. More precisely, we show the following: given a field K of characteristic p, a semiabelian variety X defined over a finite subfield of K and endowed with a regular self-map 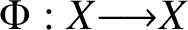$\Phi :X{\longrightarrow } X$ defined over K, a point 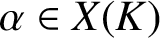$\alpha \in X(K)$ and a subvariety 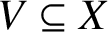$V\subseteq X$ , then the set of all nonnegative integers n such that 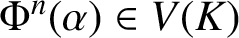$\Phi ^n(\alpha )\in V(K)$ is a union of finitely many arithmetic progressions along with a subset S with the property that there exists a positive real number A (depending only on X, 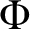$\Phi $ 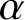, $\alpha $ and V) such that for each positive integer M,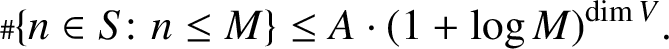

$$\begin{align*}\scriptsize\#\{n\in S\colon n\le M\}\le A\cdot (1+\log M)^{\dim V}.\end{align*}$$

Keywords

dynamical Mordell–Lang conjecturelinear recurrence sequences

MSC classification

Primary: 11B37: Recurrences
Secondary: 11G25: Varieties over finite and local fields 37P55: Arithmetic dynamics on general algebraic varieties
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 104 , Issue 3 , December 2021 , pp. 381 - 390
Check for updates
Copyright
© 2021 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

D. Ghioca and S. Saleh were partially supported by a Discovery Grant from NSERC, A. Ostafe by ARC Grants DP180100201 and DP200100355, and I. Shparlinski by ARC Grant DP200100355.

References

Bell, J. P., Ghioca, D. and Tucker, T. J., ‘The dynamical Mordell–Lang problem for Noetherian spaces’, Funct. Approx. Comment. Math. 53 (2015), 313–328.10.7169/facm/2015.53.2.7CrossRefGoogle Scholar
Bell, J. P., Ghioca, D. and Tucker, T. J., The Dynamical Mordell–Lang Conjecture, Mathematical Surveys and Monographs, 210 (American Mathematical Society, Providence, RI, 2016).10.1090/surv/210CrossRefGoogle Scholar
Corvaja, P., Ghioca, D., Scanlon, T. and Zannier, U., ‘The dynamical Mordell–Lang conjecture for endomorphisms of semiabelian varieties defined over fields of positive characteristic’, J. Inst. Math. Jussieu, to appear.Google Scholar
Corvaja, P. and Zannier, U., ‘Finiteness of odd perfect powers with four nonzero binary digits’, Ann. Inst. Fourier (Grenoble) 63 (2013), 715–731.10.5802/aif.2774CrossRefGoogle Scholar
Ghioca, D., ‘The isotrivial case in the Mordell–Lang theorem’, Trans. Amer. Math. Soc. 360(7) (2008), 3839–3856.10.1090/S0002-9947-08-04388-2CrossRefGoogle Scholar
Ghioca, D., ‘The dynamical Mordell–Lang conjecture in positive characteristic’, Trans. Amer. Math. Soc. 371(2) (2019), 1151–1167.10.1090/tran/7261CrossRefGoogle Scholar
Ghioca, D. and Tucker, T. J., ‘Periodic points, linearizing maps, and the dynamical Mordell–Lang problem’, J. Number Theory 129 (2009), 1392–1403.10.1016/j.jnt.2008.09.014CrossRefGoogle Scholar
Laurent, M., ‘Équations diophantiennes exponentielles’, Invent. Math. 78 (1984), 299–327.10.1007/BF01388597CrossRefGoogle Scholar
Moosa, R. and Scanlon, T., ‘ $F$ -structures and integral points on semiabelian varieties over finite fields’, Amer. J. Math. 126 (2004), 473–522.10.1353/ajm.2004.0017CrossRefGoogle Scholar
Schmidt, W., ‘Linear recurrence sequences’, Diophantine Approximation (Cetraro, Italy, 2000), Lecture Notes in Mathematics, 1819 (Springer, Berlin, Heidelberg, 2003), 171–247.10.1007/3-540-44979-5_4CrossRefGoogle Scholar