Fix positive integers k and n with 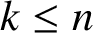$k \leq n$. Numbers 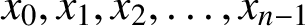$x_0, x_1, x_2, \ldots , x_{n - 1}$, each equal to $\pm {1}$, are cyclically arranged (so that 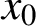$x_0$ follows 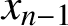$x_{n - 1}$) in that order. The problem is to find the product 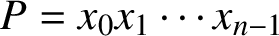$P = x_0x_1 \cdots x_{n - 1}$ of all n numbers by asking the smallest number of questions of the type 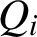$Q_i$: what is 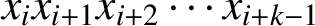$x_ix_{i + 1}x_{i + 2} \cdots x_{i+ k -1}$? (where all the subscripts are read modulo n). This paper studies the problem and some of its generalisations.