Hostname: page-component-848d4c4894-ttngx Total loading time: 0 Render date: 2024-05-19T19:19:05.331Z Has data issue: false hasContentIssue false
  • English
  • Français

GLOBAL EXISTENCE OF WEAK SOLUTIONS FOR STRONGLY DAMPED WAVE EQUATIONS WITH NONLINEAR BOUNDARY CONDITIONS AND BALANCED POTENTIALS

Part of: Hyperbolic equations and systems Dynamical problems Equations of mathematical physics and other areas of application

Published online by Cambridge University Press:  07 February 2019

JOSEPH L. SHOMBERG Open the ORCID record for JOSEPH L. SHOMBERG [Opens in a new window]
JOSEPH L. SHOMBERG*
Affiliation:
Department of Mathematics and Computer Science, Providence College, Providence, RI 02918, USA email jshomber@providence.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

We demonstrate the global existence of weak solutions to a class of semilinear strongly damped wave equations possessing nonlinear hyperbolic dynamic boundary conditions. The associated linear operator is 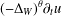$(-\unicode[STIX]{x1D6E5}_{W})^{\unicode[STIX]{x1D703}}\unicode[STIX]{x2202}_{t}u$, where 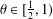$\unicode[STIX]{x1D703}\in [\frac{1}{2},1)$ and 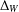$\unicode[STIX]{x1D6E5}_{W}$ is the Wentzell–Laplacian. A balance condition is assumed to hold between the nonlinearity defined on the interior of the domain and the nonlinearity on the boundary. This allows for arbitrary (supercritical) polynomial growth of each potential, as well as mixed dissipative/antidissipative behaviour.

Keywords

nonlinear hyperbolic dynamic boundary conditionsemilinear strongly damped wave equationbalance conditionglobal existenceweak solution

MSC classification

Primary: 35L71: Semilinear second-order hyperbolic equations
Secondary: 35L20: Initial-boundary value problems for second-order hyperbolic equations 35Q74: PDEs in connection with mechanics of deformable solids 74H40: Long-time behavior of solutions
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 99 , Issue 3 , June 2019 , pp. 432 - 444
Copyright
© 2019 Australian Mathematical Publishing Association Inc. 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Arendt, W., Metafune, G., Pallara, D. and Romanelli, S., ‘The Laplacian with Wentzell–Robin boundary conditions on spaces of continuous functions’, Semigroup Forum 67(2) (2003), 247–261.Google Scholar
Ball, J. M., ‘Continuity properties and global attractors of generalized semiflows and the Navier–Stokes equations’, Nonlinear Sci. 7(5) (1997), 475–502; corrected version in Mechanics: From Theory to Computation (Springer, New York, 2000), 447–474.Google Scholar
Ball, J. M., ‘Global attractors for damped semilinear wave equations’, Discrete Contin. Dyn. Syst. 10(2) (2004), 31–52.Google Scholar
Carvalho, A. N. and Cholewa, J. W., ‘Local well posedness for strongly damped wave equations with critical nonlinearities’, Bull. Austral. Math. Soc. 66(3) (2002), 443–463.Google Scholar
Cavaterra, C., Gal, C. G., Grasselli, M. and Miranville, A., ‘Phase-field systems with nonlinear coupling and dynamic boundary conditions’, Nonlinear Anal. 72(5) (2010), 2375–2399.Google Scholar
Chueshov, I. and Lasiecka, I., Von Karman Evolution Equations. Well-posedness and Long-time Dynamics, Springer Monographs in Mathematics (Springer, New York, 2010).Google Scholar
Coclite, G. M., Favini, A., Gal, C. G., Goldstein, G. R., Goldstein, J. A., Obrecht, E. and Romanelli, S., ‘The role of Wentzell boundary conditions in linear and nonlinear analysis’, in: Advances in Nonlinear Analysis: Theory, Methods and Applications, 3 (ed. Sivasundaran, S.) (Cambridge Scientific Publishers Ltd, Cambridge, 2009), 279–292.Google Scholar
D’Ovidio, M. and Garra, R., ‘Multidimensional fractional advection-dispersion equations and related stochastic processes’, Electron. J. Probab. 19 (2014), Article ID 61, 31 pages.Google Scholar
Gal, C. G., ‘On a class of degenerate parabolic equations with dynamic boundary conditions’, J. Differ. Equ. 253 (2012), 126–166.Google Scholar
Gal, C. G., ‘Sharp estimates for the global attractor of scalar reaction-diffusion equations with a Wentzell boundary condition’, J. Nonlinear Sci. 22(1) (2012), 85–106.Google Scholar
Gal, C. G. and Grasselli, M., ‘The non-isothermal Allen–Cahn equation with dynamic boundary conditions’, Discrete Contin. Dyn. Syst. 22(4) (2008), 1009–1040.Google Scholar
Gal, C. G. and Shomberg, J. L., ‘Coleman–Gurtin type equations with dynamic boundary conditions’, Phys. D 292/293 (2015), 29–45.Google Scholar
Gal, C. G. and Warma, M., ‘Well posedness and the global attractor of some quasi-linear parabolic equations with nonlinear dynamic boundary conditions’, Differential Integral Equations 23(3–4) (2010), 327–358.Google Scholar
Graber, P. J. and Shomberg, J. L., ‘Attractors for strongly damped wave equations with nonlinear hyperbolic dynamic boundary conditions’, Nonlinearity 29(4) (2016), 1171–1212.Google Scholar
Hale, J. K., Asymptotic Behavior of Dissipative Systems, Mathematical Surveys and Monographs, 25 (American Mathematical Society, Providence, RI, 1988).Google Scholar
Haraux, A. and Ôtani, M., ‘Analyticity and regularity for a class of second order evolution equations’, Evol. Equ. Control Theory 2(1) (2013), 101–117.Google Scholar
Lions, J. L., Quelques Méthodes de Résolution des Problèmes aux Limites non Linéaires (Dunod, Paris, 1969).Google Scholar
Milani, A. J. and Koksch, N. J., An Introduction to Semiflows, Monographs and Surveys in Pure and Applied Mathematics, 134 (Chapman & Hall/CRC, Boca Raton, 2005).Google Scholar
Renardy, M. and Rogers, R. C., An Introduction to Partial Differential Equations, 2nd edn, Texts in Applied Mathematics, 13 (Springer, New York, 2004).Google Scholar
Rodríguez-Bernal, A. and Tajdine, A., ‘Nonlinear balance for reaction-diffusion equations under nonlinear boundary conditions: dissipativity and blow-up’, J. Differential Equations 169 (2001), 332–372.Google Scholar
Tanabe, H., Equations of Evolution (Pitman, London, 1979).Google Scholar
Temam, R., Infinite-Dimensional Dynamical Systems in Mechanics and Physics, Applied Mathematical Sciences, 68 (Springer, New York, 1988).Google Scholar
Zheng, S., Nonlinear Evolution Equations, Monographs and Surveys in Pure and Applied Mathematics, 133 (Chapman & Hall/CRC, Boca Raton, 2004).Google Scholar