No CrossRef data available.
Article contents
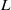 $L$-FUNCTIONS OF ELLIPTIC CURVES AND BINARY RECURRENCES
$L$-FUNCTIONS OF ELLIPTIC CURVES AND BINARY RECURRENCES
Published online by Cambridge University Press: 22 March 2013
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
Let 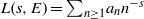 $L(s, E)= {\mathop{\sum }\nolimits}_{n\geq 1} {a}_{n} {n}^{- s} $ be the
$L(s, E)= {\mathop{\sum }\nolimits}_{n\geq 1} {a}_{n} {n}^{- s} $ be the 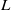 $L$-series corresponding to an elliptic curve
$L$-series corresponding to an elliptic curve 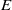 $E$ defined over
$E$ defined over 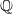 $ \mathbb{Q} $ and
$ \mathbb{Q} $ and 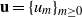 $\mathbf{u} = \mathop{\{ {u}_{m} \} }\nolimits_{m\geq 0} $ be a nondegenerate binary recurrence sequence. We prove that if
$\mathbf{u} = \mathop{\{ {u}_{m} \} }\nolimits_{m\geq 0} $ be a nondegenerate binary recurrence sequence. We prove that if 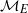 ${ \mathcal{M} }_{E} $ is the set of
${ \mathcal{M} }_{E} $ is the set of  $n$ such that
$n$ such that 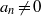 ${a}_{n} \not = 0$ and
${a}_{n} \not = 0$ and 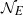 ${ \mathcal{N} }_{E} $ is the subset of
${ \mathcal{N} }_{E} $ is the subset of 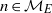 $n\in { \mathcal{M} }_{E} $ such that
$n\in { \mathcal{M} }_{E} $ such that 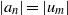 $\vert {a}_{n} \vert = \vert {u}_{m} \vert $ holds with some integer
$\vert {a}_{n} \vert = \vert {u}_{m} \vert $ holds with some integer 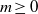 $m\geq 0$, then
$m\geq 0$, then 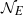 ${ \mathcal{N} }_{E} $ is of density
${ \mathcal{N} }_{E} $ is of density 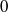 $0$ as a subset of
$0$ as a subset of 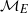 ${ \mathcal{M} }_{E} $.
${ \mathcal{M} }_{E} $.
Information
- Type
- Research Article
- Information
- Bulletin of the Australian Mathematical Society , Volume 88 , Issue 3 , December 2013 , pp. 509 - 519
- Copyright
- Copyright ©2013 Australian Mathematical Publishing Association Inc.
References
Canfield, E. R., Erdős, P. and Pomerance, C., ‘On a problem of Oppenheim concerning factorisatio numerorum’, J. Number Theory 17 (1983), 1–28.CrossRefGoogle Scholar
Cojocaru, A. C., ‘Questions about the reductions modulo primes of an elliptic curve’, in: Number Theory: Proceedings of the 7th Conference of the Canadian Number Theory Association (Montreal, 2002), CRM Proceedings and Lecture Notes, 36 (eds. Kisilevsky, H.
and
Goren, E.) (American Mathematical Society, Providence, RI, 2004), 61–79.Google Scholar
Deuring, M., ‘Die Typen der Multiplikatorenringe elliptischer Functionenkörper’, Abh. Math. Sem. Hansischen Univ. 14 (1941), 197–272.CrossRefGoogle Scholar
Elkies, N. D., ‘The existence of infinitely many supersingular primes for every elliptic curve over  $ \mathbb{Q} $’, Invent. Math. 89 (1987), 561–567.CrossRefGoogle Scholar
$ \mathbb{Q} $’, Invent. Math. 89 (1987), 561–567.CrossRefGoogle Scholar
Hall, R. R. and Tenenbaum, G., Divisors (Cambridge University Press, Cambridge, 1988).Google Scholar
Luca, F. and Yalçiner, A., ‘ $L$-functions of elliptic curves and Fibonacci numbers’, Fibonacci Quart. to appear.Google Scholar
$L$-functions of elliptic curves and Fibonacci numbers’, Fibonacci Quart. to appear.Google Scholar
Lucas, E., ‘Théorie des fonctions numériques simplement périodiques’, Amer. J. Math. 1 (1878), 189–240; 289–321.CrossRefGoogle Scholar
Serre, J.-P., ‘Quelques applications du théorème de densité de Chebotarev’, Publ. Math. Inst. Hautes Études Sci. 54 (1981), 123–201.Google Scholar
Somer, L., ‘Which second-order linear integral recurrences have almost all primes as divisors?’, Fibonacci Quart. 17 (1979), 111–116.Google Scholar
Stewart, C. L., Divisor Properties of Arithmetical Sequences, PhD Thesis, University of Cambridge, 1976.Google Scholar
Wirsing, E., ‘Das asymptotische Verhalten von Summen über multiplikative Funktionen’, Math. Ann. 143 (1961), 75–102.Google Scholar

