Hostname: page-component-76fb5796d-skm99 Total loading time: 0 Render date: 2024-04-28T13:32:46.362Z Has data issue: false hasContentIssue false
  • English
  • Français

ON A CLASS OF NONLINEAR SCHRÖDINGER EQUATIONS ON FINITE GRAPHS

Part of: Equations of mathematical physics and other areas of application Partial differential equations Miscellaneous topics - Partial differential equations

Published online by Cambridge University Press:  20 February 2020

SHOUDONG MAN Open the ORCID record for SHOUDONG MAN [Opens in a new window]
SHOUDONG MAN*
Affiliation:
Department of Mathematics,Tianjin University of Finance and Economics, Tianjin300222, PR China email manshoudong@163.com, shoudongmantj@tjufe.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

Suppose that 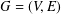$G=(V,E)$ is a finite graph with the vertex set 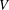$V$ and the edge set 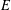$E$. Let 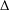$\unicode[STIX]{x1D6E5}$ be the usual graph Laplacian. Consider the nonlinear Schrödinger equation of the form

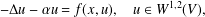$$\begin{eqnarray}-\unicode[STIX]{x1D6E5}u-\unicode[STIX]{x1D6FC}u=f(x,u),\quad u\in W^{1,2}(V),\end{eqnarray}$$
on the graph $G$, where 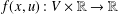$f(x,u):V\times \mathbb{R}\rightarrow \mathbb{R}$ is a nonlinear real-valued function and $\unicode[STIX]{x1D6FC}$ is a parameter. We prove an integral inequality on $G$ under the assumption that 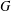$G$ satisfies the curvature-dimension type inequality 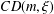$CD(m,\unicode[STIX]{x1D709})$. Then by using the Poincaré–Sobolev inequality, the Trudinger–Moser inequality and the integral inequality on 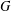$G$, we prove that there is a nontrivial solution to the nonlinear Schrödinger equation if 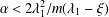$\unicode[STIX]{x1D6FC}<2\unicode[STIX]{x1D706}_{1}^{2}/m(\unicode[STIX]{x1D706}_{1}-\unicode[STIX]{x1D709})$, where 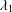$\unicode[STIX]{x1D706}_{1}$ is the first positive eigenvalue of the graph Laplacian.

Keywords

Laplacian on graphscurvature-dimension type inequalitySchrödinger equation on finite graphs

MSC classification

Primary: 35Q55: NLS-like equations (nonlinear Schrödinger)
Secondary: 35A15: Variational methods 35R02: Partial differential equations on graphs and networks (ramified or polygonal spaces)
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 101 , Issue 3 , June 2020 , pp. 477 - 487
Copyright
© 2020 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The author is supported by the National Natural Science Foundation of China (Grant No. 11601368).

References

Ambrosetti, A. and Rabinowitz, P., ‘Dual variational methods in critical point theory and applications’, J. Funct. Anal. 14 (1973), 349–381.10.1016/0022-1236(73)90051-7CrossRefGoogle Scholar
Adimurthi, A. and Yang, Y., ‘An interpolation of Hardy inequality and Trudinger–Moser inequality in ℝN and its applications’, Int. Math. Res. Not. IMRN 2010(13) (2010), 2394–2426.Google Scholar
Bauer, F., Chung, F., Lin, Y. and Liu, Y., ‘Curvature aspects of graphs’, Proc. Amer. Math. Soc. 145 (2017), 2033–2042.10.1090/proc/13145CrossRefGoogle Scholar
Chung, F., Spectral Graph Theory, CBMS Regional Conference Series in Mathematics, 92 (American Mathematical Society, Providence, RI, 1997).Google Scholar
do Ó, J. M. B., ‘Semilinear Dirichlet problems for the N-Laplacian in ℝN with nonlinearities in critical growth range’, Differential Integral Equations 9 (1996), 967–979.Google Scholar
Grigoryan, A., Lin, Y. and Yang, Y., ‘Yamabe type equations on graphs’, J. Differential Equations 261(9) (2016), 4924–4943.10.1016/j.jde.2016.07.011CrossRefGoogle Scholar
Grigoryan, A., Lin, Y. and Yang, Y., ‘Kazdan–Warner equation on graphs’, Calc. Var. Partial Differential Equations 55(4) (2016), 92–113.10.1007/s00526-016-1042-3CrossRefGoogle Scholar
Lin, Y. and Yau, S. T., ‘Ricci curvature and eigenvalue estimation on locally finite graphs’, Math. Res. Lett. 17(2) (2010), 345–358.10.4310/MRL.2010.v17.n2.a13CrossRefGoogle Scholar
Moser, J., ‘A sharp form of an inequality by N. Trudinger’, Indiana Univ. Math. J. 20 (1970), 1077–1092.10.1512/iumj.1971.20.20101CrossRefGoogle Scholar
Xuan, B., Variational Methods: Theory and Applications (University of Science and Technology of China Press, Hefei, 2006).Google Scholar