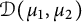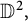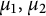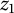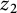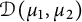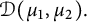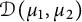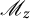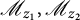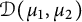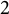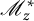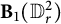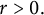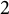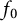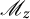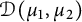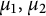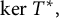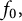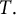1 Introduction and preliminaries
The aim of this paper is to obtain a bidisc counter-part of the theory of Dirichlet-type spaces of the open unit disc as presented in [Reference Richter26] (see [Reference Chavan, Gupta and Reza8] for a ball counter-part of this theory). Throughout this paper,
![]() $\mathbb D$
denotes the open unit disc
$\mathbb D$
denotes the open unit disc
![]() $\{z \in \mathbb C : |z|<1\}$
in the complex plane
$\{z \in \mathbb C : |z|<1\}$
in the complex plane
![]() $\mathbb C.$
Recall that Dirichlet-type spaces of
$\mathbb C.$
Recall that Dirichlet-type spaces of
![]() $\mathbb D$
are model spaces for the class of cyclic analytic
$\mathbb D$
are model spaces for the class of cyclic analytic
![]() $2$
-isometries (see [Reference Richter26]). Thus to arrive at an appropriate notion of the Dirichlet-type spaces of the unit bidisc
$2$
-isometries (see [Reference Richter26]). Thus to arrive at an appropriate notion of the Dirichlet-type spaces of the unit bidisc
![]() $\mathbb D^2$
, it is helpful to look for function spaces which support the class of
$\mathbb D^2$
, it is helpful to look for function spaces which support the class of
![]() $2$
-isometries naturally associated with
$2$
-isometries naturally associated with
![]() $\mathbb D^2.$
Let us first recall the definition of such
$\mathbb D^2.$
Let us first recall the definition of such
![]() $2$
-isometries.
$2$
-isometries.
For a complex Hilbert space
![]() $\mathcal H,$
let
$\mathcal H,$
let
![]() $\mathcal B(\mathcal H)$
denote the
$\mathcal B(\mathcal H)$
denote the
![]() $C^*$
-algebra of bounded linear operators on
$C^*$
-algebra of bounded linear operators on
![]() $\mathcal H.$
For a positive integer
$\mathcal H.$
For a positive integer
![]() $d,$
a commuting d-tuple T on
$d,$
a commuting d-tuple T on
![]() $\mathcal H$
is the d-tuple
$\mathcal H$
is the d-tuple
![]() $(T_1, \ldots , T_d)$
of operators
$(T_1, \ldots , T_d)$
of operators
![]() $T_1, \ldots , T_d \in \mathcal B(\mathcal H)$
satisfying
$T_1, \ldots , T_d \in \mathcal B(\mathcal H)$
satisfying
![]() $T_iT_j=T_jT_i, 1 \leqslant i \neq j \leqslant d.$
Let
$T_iT_j=T_jT_i, 1 \leqslant i \neq j \leqslant d.$
Let
![]() $T=(T_1, \ldots , T_d)$
be a commuting d-tuple on
$T=(T_1, \ldots , T_d)$
be a commuting d-tuple on
![]() $\mathcal H$
. We say that
$\mathcal H$
. We say that
![]() $T=(T_1, \ldots , T_d)$
is a toral isometry if
$T=(T_1, \ldots , T_d)$
is a toral isometry if
![]() $T_1, \ldots , T_d$
are isometries. Following [Reference Agler1, Reference Athavale and Sholapurkar5, Reference Richter26], T is said to be a toral
$T_1, \ldots , T_d$
are isometries. Following [Reference Agler1, Reference Athavale and Sholapurkar5, Reference Richter26], T is said to be a toral
![]() $2$
-isometry if
$2$
-isometry if
A toral isometry is necessarily a toral
![]() $2$
-isometry, but the converse is not true (see [Reference Athavale and Sholapurkar5, Example 1]).
$2$
-isometry, but the converse is not true (see [Reference Athavale and Sholapurkar5, Example 1]).
To propose a successful analog of Dirichlet-type spaces on
![]() $\mathbb D^2,$
it is helpful to examine examples of toral
$\mathbb D^2,$
it is helpful to examine examples of toral
![]() $2$
-isometries arising from function spaces. Since the operator of multiplication by the coordinate function on the classical Dirichlet space
$2$
-isometries arising from function spaces. Since the operator of multiplication by the coordinate function on the classical Dirichlet space
![]() $\mathcal D(\mathbb D)$
is a
$\mathcal D(\mathbb D)$
is a
![]() $2$
-isometry, it is natural to seek the classical Dirichlet space of the unit bidisc. Recall that the Dirichlet space
$2$
-isometry, it is natural to seek the classical Dirichlet space of the unit bidisc. Recall that the Dirichlet space
![]() $\mathcal D(\mathbb D) \otimes \mathcal D(\mathbb D)$
of
$\mathcal D(\mathbb D) \otimes \mathcal D(\mathbb D)$
of
![]() $\mathbb D^2$
is given by
$\mathbb D^2$
is given by
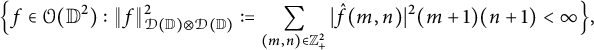 $$ \begin{align*} \Big\{f \in \mathcal O(\mathbb D^2): \|f\|^2_{\mathcal D(\mathbb D) \otimes \mathcal D(\mathbb D)}:=\sum_{(m, n) \in \mathbb Z^2_+}|\hat{f}(m, n)|^2 (m+1)(n+1)< \infty\Big\}, \end{align*} $$
$$ \begin{align*} \Big\{f \in \mathcal O(\mathbb D^2): \|f\|^2_{\mathcal D(\mathbb D) \otimes \mathcal D(\mathbb D)}:=\sum_{(m, n) \in \mathbb Z^2_+}|\hat{f}(m, n)|^2 (m+1)(n+1)< \infty\Big\}, \end{align*} $$
where
![]() $\mathcal O(\Omega )$
denotes the space of holomorphic functions on a domain
$\mathcal O(\Omega )$
denotes the space of holomorphic functions on a domain
![]() $\Omega , \mathbb Z_+$
denotes the set of nonnegative integers and
$\Omega , \mathbb Z_+$
denotes the set of nonnegative integers and
![]() $\hat {f}$
denotes the Fourier transform of
$\hat {f}$
denotes the Fourier transform of
![]() $f.$
It turns out that if
$f.$
It turns out that if
![]() $\mathscr M_{z_1}$
and
$\mathscr M_{z_1}$
and
![]() $\mathscr M_{z_2}$
are the operators of multiplication by the coordinate functions
$\mathscr M_{z_2}$
are the operators of multiplication by the coordinate functions
![]() $z_1$
and
$z_1$
and
![]() $z_2,$
respectively, on
$z_2,$
respectively, on
![]() $\mathcal D(\mathbb D) \otimes \mathcal D(\mathbb D),$
then the commuting pair
$\mathcal D(\mathbb D) \otimes \mathcal D(\mathbb D),$
then the commuting pair
![]() $(\mathscr M_{z_1}, \mathscr M_{z_2})$
satisfies (1.1) for
$(\mathscr M_{z_1}, \mathscr M_{z_2})$
satisfies (1.1) for
![]() $1 \leqslant i=j \leqslant 2,$
but it fails to satisfy (1.1) for
$1 \leqslant i=j \leqslant 2,$
but it fails to satisfy (1.1) for
![]() $1 \leqslant i \neq j \leqslant 2.$
This failure may be attributed to the fact that the mapping
$1 \leqslant i \neq j \leqslant 2.$
This failure may be attributed to the fact that the mapping
![]() $(m, n) \mapsto \|z^m_1z^n_2\|^2$
is a polynomial of bi-degree
$(m, n) \mapsto \|z^m_1z^n_2\|^2$
is a polynomial of bi-degree
![]() $(1, 1).$
Interestingly, there is a “natural” choice
$(1, 1).$
Interestingly, there is a “natural” choice
![]() $\mathcal D(\mathbb D^2)$
of the Dirichlet space containing
$\mathcal D(\mathbb D^2)$
of the Dirichlet space containing
![]() $\mathcal D(\mathbb D) \otimes \mathcal D(\mathbb D)$
for which the associated pair
$\mathcal D(\mathbb D) \otimes \mathcal D(\mathbb D)$
for which the associated pair
![]() $(\mathscr M_{z_1}, \mathscr M_{z_2})$
is a toral
$(\mathscr M_{z_1}, \mathscr M_{z_2})$
is a toral
![]() $2$
-isometry:
$2$
-isometry:
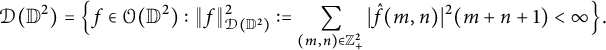 $$ \begin{align*}\mathcal D(\mathbb D^2)=\Big\{f \in \mathcal O(\mathbb D^2): \|f\|^2_{\mathcal D(\mathbb D^2)}:=\sum_{(m, n) \in \mathbb Z^2_+}|\hat{f}(m, n)|^2 (m+n+1) < \infty\Big\}.\end{align*} $$
$$ \begin{align*}\mathcal D(\mathbb D^2)=\Big\{f \in \mathcal O(\mathbb D^2): \|f\|^2_{\mathcal D(\mathbb D^2)}:=\sum_{(m, n) \in \mathbb Z^2_+}|\hat{f}(m, n)|^2 (m+n+1) < \infty\Big\}.\end{align*} $$
The norm
![]() $\|\cdot \|_{\mathcal D(\mathbb D^2)}$
can also be written as follows:
$\|\cdot \|_{\mathcal D(\mathbb D^2)}$
can also be written as follows:
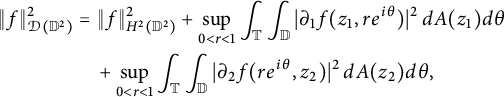 $$ \begin{align} \|f\|^2_{\mathcal D(\mathbb D^2)} &= \|f\|^2_{H^2(\mathbb D^2)} + \sup_{0 < r < 1} \int_{\mathbb T} \int_{\mathbb D}|\partial_1 f(z_1, re^{i \theta})|^2 \,dA(z_1)d\theta \notag \\& \quad + \sup_{0 < r < 1} \int_{\mathbb T} \int_{\mathbb D}|\partial_2 f(re^{i \theta}, z_2)|^2 \,dA(z_2)d\theta, \end{align} $$
$$ \begin{align} \|f\|^2_{\mathcal D(\mathbb D^2)} &= \|f\|^2_{H^2(\mathbb D^2)} + \sup_{0 < r < 1} \int_{\mathbb T} \int_{\mathbb D}|\partial_1 f(z_1, re^{i \theta})|^2 \,dA(z_1)d\theta \notag \\& \quad + \sup_{0 < r < 1} \int_{\mathbb T} \int_{\mathbb D}|\partial_2 f(re^{i \theta}, z_2)|^2 \,dA(z_2)d\theta, \end{align} $$
where
![]() $d\theta $
(resp.
$d\theta $
(resp.
![]() $dA$
) denotes the normalized Lebesgue arc-length (resp. area) measure on
$dA$
) denotes the normalized Lebesgue arc-length (resp. area) measure on
![]() $\mathbb T$
(resp.
$\mathbb T$
(resp.
![]() $\mathbb D$
). Recall that the Hardy space
$\mathbb D$
). Recall that the Hardy space
![]() $H^2(\mathbb D^2)$
of the unit bidisc
$H^2(\mathbb D^2)$
of the unit bidisc
![]() $\mathbb D^2$
is the reproducing kernel Hilbert space (see [Reference Paulsen and Raghupathi23] for the definition of the reproducing kernel Hilbert space) associated with the Cauchy kernel
$\mathbb D^2$
is the reproducing kernel Hilbert space (see [Reference Paulsen and Raghupathi23] for the definition of the reproducing kernel Hilbert space) associated with the Cauchy kernel
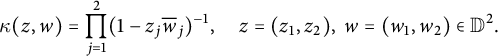 $$ \begin{align*} \kappa(z, w)=\prod_{j=1}^2(1-z_j\overline{w}_j)^{-1}, \quad z=(z_1, z_2), ~w=(w_1, w_2) \in \mathbb D^2. \end{align*} $$
$$ \begin{align*} \kappa(z, w)=\prod_{j=1}^2(1-z_j\overline{w}_j)^{-1}, \quad z=(z_1, z_2), ~w=(w_1, w_2) \in \mathbb D^2. \end{align*} $$
It is worth noting that for any
![]() $f \in H^2(\mathbb D^2),$
$f \in H^2(\mathbb D^2),$
(see [Reference Rudin27, Section 3.4]).
For a nonempty subset
![]() $\Omega $
of
$\Omega $
of
![]() $\mathbb C,$
let
$\mathbb C,$
let
![]() $M_+(\Omega )$
denote the set of finite positive Borel measures on
$M_+(\Omega )$
denote the set of finite positive Borel measures on
![]() $\Omega .$
Let
$\Omega .$
Let
![]() $P_{\mu }(w)$
denote the Poisson integral
$P_{\mu }(w)$
denote the Poisson integral
![]() $\int _{\mathbb T} \frac {1-|w|^2}{|w-\zeta |^2}d\mu (\zeta )$
of the measure
$\int _{\mathbb T} \frac {1-|w|^2}{|w-\zeta |^2}d\mu (\zeta )$
of the measure
![]() $\mu \in M_+(\mathbb T).$
For future reference, we record the following consequence of the Fubini’s theorem (see [Reference Rudin28, Theorem 8.8]) and the fact that the mapping
$\mu \in M_+(\mathbb T).$
For future reference, we record the following consequence of the Fubini’s theorem (see [Reference Rudin28, Theorem 8.8]) and the fact that the mapping
![]() $r \mapsto \int _{\mathbb T} |f(z, re^{i \theta })|^2 d\theta $
is increasing.
$r \mapsto \int _{\mathbb T} |f(z, re^{i \theta })|^2 d\theta $
is increasing.
Lemma 1.1 For
![]() $f \in \mathcal O(\mathbb D^{2})$
and
$f \in \mathcal O(\mathbb D^{2})$
and
![]() $\mu \in M_+(\mathbb D)$
, the extended real-valued mapping
$\mu \in M_+(\mathbb D)$
, the extended real-valued mapping
![]() $\phi (r)= \int _{\mathbb T} \int _{\mathbb D}|f(z, re^{i \theta })|^2 d\mu (z)d\theta , r \in (0, 1),$
is increasing.
$\phi (r)= \int _{\mathbb T} \int _{\mathbb D}|f(z, re^{i \theta })|^2 d\mu (z)d\theta , r \in (0, 1),$
is increasing.
The formula (1.2) together with Richter’s notion of Dirichlet-type spaces (see [Reference Richter26, Section 3]) motivates us to the following:
Definition 1.2 For
![]() $\mu _1, \mu _2 \in M_+(\mathbb T)$
and
$\mu _1, \mu _2 \in M_+(\mathbb T)$
and
![]() $f \in \mathcal O(\mathbb D^2),$
the Dirichlet integral
$f \in \mathcal O(\mathbb D^2),$
the Dirichlet integral
![]() $D_{\mu _1, \mu _2}(f)$
of f is given by
$D_{\mu _1, \mu _2}(f)$
of f is given by
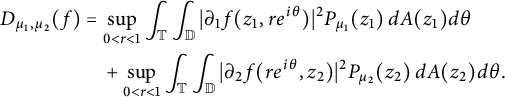 $$ \begin{align*} D_{\mu_1, \mu_2}(f) &= \sup_{0 < r < 1} \int_{\mathbb T} \int_{\mathbb D}|\partial_1 f(z_1, re^{i \theta})|^2 P_{\mu_1}(z_1) \,dA(z_1)d\theta \\& \quad + \sup_{0 < r < 1} \int_{\mathbb T} \int_{\mathbb D}|\partial_2 f(re^{i \theta}, z_2)|^2 P_{\mu_2}(z_2) \,dA(z_2)d\theta. \end{align*} $$
$$ \begin{align*} D_{\mu_1, \mu_2}(f) &= \sup_{0 < r < 1} \int_{\mathbb T} \int_{\mathbb D}|\partial_1 f(z_1, re^{i \theta})|^2 P_{\mu_1}(z_1) \,dA(z_1)d\theta \\& \quad + \sup_{0 < r < 1} \int_{\mathbb T} \int_{\mathbb D}|\partial_2 f(re^{i \theta}, z_2)|^2 P_{\mu_2}(z_2) \,dA(z_2)d\theta. \end{align*} $$
If either
![]() $\mu _1$
or
$\mu _1$
or
![]() $\mu _2$
is
$\mu _2$
is
![]() $0,$
then the Dirichlet-type space
$0,$
then the Dirichlet-type space
![]() $\mathcal D(\mu _1, \mu _2)$
is the space of functions
$\mathcal D(\mu _1, \mu _2)$
is the space of functions
![]() $f \in H^2(\mathbb D^2)$
satisfying
$f \in H^2(\mathbb D^2)$
satisfying
![]() $D_{\mu _1, \mu _2}(f) < \infty .$
Otherwise, we set
$D_{\mu _1, \mu _2}(f) < \infty .$
Otherwise, we set
![]() $\mathcal D(\mu _1, \mu _2) = \{f \in \mathcal O(\mathbb D^2) : D_{\mu _1, \mu _2}(f) < \infty \}.$
$\mathcal D(\mu _1, \mu _2) = \{f \in \mathcal O(\mathbb D^2) : D_{\mu _1, \mu _2}(f) < \infty \}.$
Before we define a norm on the Dirichlet-type space
![]() $\mathcal D(\mu _1, \mu _2),$
we present a
$\mathcal D(\mu _1, \mu _2),$
we present a
![]() $2$
-variable analog of [Reference Richter26, Lemma 3.1].
$2$
-variable analog of [Reference Richter26, Lemma 3.1].
Lemma 1.3 For
![]() $\mu _1, \mu _2 \in M_+(\mathbb T), \mathcal D(\mu _1, \mu _2) \subseteq H^2(\mathbb D^2).$
$\mu _1, \mu _2 \in M_+(\mathbb T), \mathcal D(\mu _1, \mu _2) \subseteq H^2(\mathbb D^2).$
Proof By the definition of
![]() $\mathcal D(\mu _1, \mu _2),$
we may assume that both measures
$\mathcal D(\mu _1, \mu _2),$
we may assume that both measures
![]() $\mu _1$
and
$\mu _1$
and
![]() $\mu _2$
are nonzero. Note that
$\mu _2$
are nonzero. Note that
Thus, for any
![]() $f(z_1, z_2)=\sum _{m, n =0}^{\infty }a_{m, n}\,z^m_1z^n_2 \in \mathcal D(\mu _1, \mu _2),$
$f(z_1, z_2)=\sum _{m, n =0}^{\infty }a_{m, n}\,z^m_1z^n_2 \in \mathcal D(\mu _1, \mu _2),$
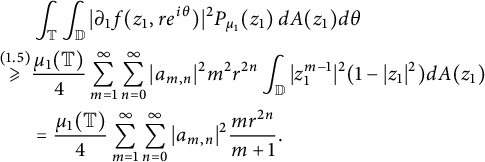 $$ \begin{align*} & \int_{\mathbb T} \int_{\mathbb D}|\partial_1 f(z_1, re^{i \theta})|^2 P_{\mu_1}(z_1) \,dA(z_1)d\theta \\ \overset{(1.5)} \geqslant & \frac{\mu_1(\mathbb T)}{4} \sum_{m =1}^{\infty} \sum_{n=0}^{\infty} |a_{m, n}|^2 m^2 r^{2n} \int_{\mathbb D} |z^{m-1}_1|^2 (1-|z_1|^2)dA(z_1) \\ &= \frac{\mu_1(\mathbb T)}{4} \sum_{m =1}^{\infty} \sum_{n=0}^{\infty} |a_{m, n}|^2 \frac{m r^{2n}}{m+1}. \end{align*} $$
$$ \begin{align*} & \int_{\mathbb T} \int_{\mathbb D}|\partial_1 f(z_1, re^{i \theta})|^2 P_{\mu_1}(z_1) \,dA(z_1)d\theta \\ \overset{(1.5)} \geqslant & \frac{\mu_1(\mathbb T)}{4} \sum_{m =1}^{\infty} \sum_{n=0}^{\infty} |a_{m, n}|^2 m^2 r^{2n} \int_{\mathbb D} |z^{m-1}_1|^2 (1-|z_1|^2)dA(z_1) \\ &= \frac{\mu_1(\mathbb T)}{4} \sum_{m =1}^{\infty} \sum_{n=0}^{\infty} |a_{m, n}|^2 \frac{m r^{2n}}{m+1}. \end{align*} $$
A similar estimate using (1.5) gives
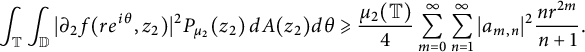 $$ \begin{align*} \int_{\mathbb T} \int_{\mathbb D}|\partial_2 f(re^{i \theta}, z_2)|^2 P_{\mu_2}(z_2) \,dA(z_2)d\theta \geqslant \frac{\mu_2(\mathbb T)}{4} \sum_{m =0}^{\infty} \sum_{n=1}^{\infty} |a_{m, n}|^2 \frac{nr^{2m}}{n+1}. \end{align*} $$
$$ \begin{align*} \int_{\mathbb T} \int_{\mathbb D}|\partial_2 f(re^{i \theta}, z_2)|^2 P_{\mu_2}(z_2) \,dA(z_2)d\theta \geqslant \frac{\mu_2(\mathbb T)}{4} \sum_{m =0}^{\infty} \sum_{n=1}^{\infty} |a_{m, n}|^2 \frac{nr^{2m}}{n+1}. \end{align*} $$
Since
![]() $f \in \mathcal D(\mu _1, \mu _2),$
$f \in \mathcal D(\mu _1, \mu _2),$
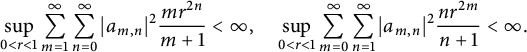 $$ \begin{align*} \sup_{0 < r < 1} \sum_{m =1}^{\infty} \sum_{n=0}^{\infty} |a_{m, n}|^2 \frac{m r^{2n}}{m+1} < \infty, \quad \sup_{0 < r < 1} \sum_{m =0}^{\infty} \sum_{n=1}^{\infty} |a_{m, n}|^2 \frac{nr^{2m}}{n+1} < \infty. \end{align*} $$
$$ \begin{align*} \sup_{0 < r < 1} \sum_{m =1}^{\infty} \sum_{n=0}^{\infty} |a_{m, n}|^2 \frac{m r^{2n}}{m+1} < \infty, \quad \sup_{0 < r < 1} \sum_{m =0}^{\infty} \sum_{n=1}^{\infty} |a_{m, n}|^2 \frac{nr^{2m}}{n+1} < \infty. \end{align*} $$
It is now easy to see using the monotone convergence theorem (see [Reference Rudin28, Theorem 1.26]) that f belongs to
![]() $H^2(\mathbb D^2).$
$H^2(\mathbb D^2).$
In view of Lemmas 1.1 and 1.3, the Dirichlet-type space
![]() $\mathcal D(\mu _1, \mu _2)$
can be endowed with the norm
$\mathcal D(\mu _1, \mu _2)$
can be endowed with the norm
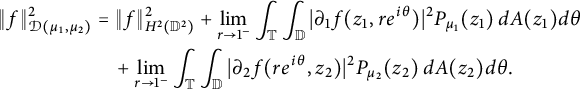 $$ \begin{align*} \|f\|^2_{\mathcal D(\mu_1, \mu_2)} &= \|f\|^2_{H^2(\mathbb D^2)} + \lim_{r \rightarrow 1^{-}} \int_{\mathbb T} \int_{\mathbb D}|\partial_1 f(z_1, re^{i \theta})|^2 P_{\mu_1}(z_1) \,dA(z_1)d\theta \\& \quad + \lim_{r \rightarrow 1^{-}} \int_{\mathbb T} \int_{\mathbb D}|\partial_2 f(re^{i \theta}, z_2)|^2 P_{\mu_2}(z_2) \,dA(z_2)d\theta. \end{align*} $$
$$ \begin{align*} \|f\|^2_{\mathcal D(\mu_1, \mu_2)} &= \|f\|^2_{H^2(\mathbb D^2)} + \lim_{r \rightarrow 1^{-}} \int_{\mathbb T} \int_{\mathbb D}|\partial_1 f(z_1, re^{i \theta})|^2 P_{\mu_1}(z_1) \,dA(z_1)d\theta \\& \quad + \lim_{r \rightarrow 1^{-}} \int_{\mathbb T} \int_{\mathbb D}|\partial_2 f(re^{i \theta}, z_2)|^2 P_{\mu_2}(z_2) \,dA(z_2)d\theta. \end{align*} $$
We see that
![]() $\mathcal D(\mu _1, \mu _2)$
is a reproducing kernel Hilbert space (see Lemma 3.1).
$\mathcal D(\mu _1, \mu _2)$
is a reproducing kernel Hilbert space (see Lemma 3.1).
The present paper is devoted to the study of Dirichlet-type spaces with efforts to understand the bidisc counter-part of the work carried out in [Reference Richter26]. Before we state the main results of this paper, we need some definitions.
For a positive integer
![]() $d,$
let
$d,$
let
![]() $\Omega $
be a domain in
$\Omega $
be a domain in
![]() $\mathbb C^d$
, and let
$\mathbb C^d$
, and let
![]() $\mathscr H$
be a Hilbert space such that
$\mathscr H$
be a Hilbert space such that
![]() $\mathscr H \subseteq \mathcal O(\Omega ).$
A function
$\mathscr H \subseteq \mathcal O(\Omega ).$
A function
![]() $\varphi : \Omega \rightarrow \mathbb C$
is said to be a multiplier of
$\varphi : \Omega \rightarrow \mathbb C$
is said to be a multiplier of
![]() $\mathscr H$
if
$\mathscr H$
if
![]() $\varphi f \in \mathscr H$
for every
$\varphi f \in \mathscr H$
for every
![]() $f \in \mathscr H.$
For a nonempty subset U of
$f \in \mathscr H.$
For a nonempty subset U of
![]() $\Omega ,$
we say that Gleason’s problem can be solved for
$\Omega ,$
we say that Gleason’s problem can be solved for
![]() $\mathscr H$
over U if for every
$\mathscr H$
over U if for every
![]() $f \in \mathscr H$
and
$f \in \mathscr H$
and
![]() $\lambda = (\lambda _1, \ldots , \lambda _d) \in U,$
there exist functions
$\lambda = (\lambda _1, \ldots , \lambda _d) \in U,$
there exist functions
![]() $g_1, \ldots , g_d$
in
$g_1, \ldots , g_d$
in
![]() $\mathscr H$
such that
$\mathscr H$
such that
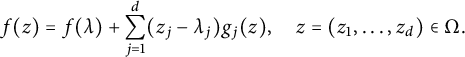 $$ \begin{align*} f(z)=f(\lambda) + \sum_{j=1}^d (z_j-\lambda_j)g_j(z), \quad z=(z_1, \ldots, z_d) \in \Omega. \end{align*} $$
$$ \begin{align*} f(z)=f(\lambda) + \sum_{j=1}^d (z_j-\lambda_j)g_j(z), \quad z=(z_1, \ldots, z_d) \in \Omega. \end{align*} $$
We say that Gleason’s problem can be solved for
![]() $\mathscr H$
if Gleason’s problem can be solved for
$\mathscr H$
if Gleason’s problem can be solved for
![]() $\mathscr H$
over
$\mathscr H$
over
![]() $\Omega $
(the reader is referred to [Reference Zhu31] for a solution of Gleason’s problem for Bergman and Bloch spaces of the unit ball). It turns out that Gleason’s problem can be solved for
$\Omega $
(the reader is referred to [Reference Zhu31] for a solution of Gleason’s problem for Bergman and Bloch spaces of the unit ball). It turns out that Gleason’s problem can be solved for
![]() $H^2(\mathbb D^d)$
(see Remark 5.2).
$H^2(\mathbb D^d)$
(see Remark 5.2).
Definition 1.4 Let
![]() $\Omega $
be a domain in
$\Omega $
be a domain in
![]() $\mathbb C^d$
, and let
$\mathbb C^d$
, and let
![]() $\mathscr H$
be a Hilbert space such that
$\mathscr H$
be a Hilbert space such that
![]() $\mathscr H \subseteq \mathcal O(\Omega ).$
We say that
$\mathscr H \subseteq \mathcal O(\Omega ).$
We say that
![]() $\mathscr H$
has the j-division property,
$\mathscr H$
has the j-division property,
![]() $j=1, \ldots , d,$
if
$j=1, \ldots , d,$
if
![]() $\frac {f(z)}{z_j-\lambda _j}$
defines a function in
$\frac {f(z)}{z_j-\lambda _j}$
defines a function in
![]() $\mathscr H$
whenever
$\mathscr H$
whenever
![]() $\lambda \in \Omega , f \in \mathscr H$
and
$\lambda \in \Omega , f \in \mathscr H$
and
![]() $\{z \in \Omega : z_j =\lambda _j\}$
is contained in
$\{z \in \Omega : z_j =\lambda _j\}$
is contained in
![]() $Z(f),$
the zero set of
$Z(f),$
the zero set of
![]() $f.$
If
$f.$
If
![]() $\mathscr H$
has j-division property for every
$\mathscr H$
has j-division property for every
![]() $j=1, \ldots , d,$
then we say that
$j=1, \ldots , d,$
then we say that
![]() $\mathscr H$
has the division property.
$\mathscr H$
has the division property.
In case of
![]() $d=1,$
this property appeared in [Reference Aleman and Richter4, Definition 1.1]. One of the main results of this paper shows that
$d=1,$
this property appeared in [Reference Aleman and Richter4, Definition 1.1]. One of the main results of this paper shows that
![]() $\mathcal D(\mu _1, \mu _2)$
has the division property. In what follows, we require a generalization of the notion of the wandering subspace introduced by Halmos (see [Reference Halmos20, p. 103]).
$\mathcal D(\mu _1, \mu _2)$
has the division property. In what follows, we require a generalization of the notion of the wandering subspace introduced by Halmos (see [Reference Halmos20, p. 103]).
Definition 1.5 Let
![]() $T=(T_1, \ldots , T_d)$
be a commuting d-tuple on
$T=(T_1, \ldots , T_d)$
be a commuting d-tuple on
![]() $\mathcal H.$
A closed subspace
$\mathcal H.$
A closed subspace
![]() $\mathcal W$
of
$\mathcal W$
of
![]() $\mathcal H$
is said to be wandering for T if for every
$\mathcal H$
is said to be wandering for T if for every
![]() $i=1, \ldots , d,$
$i=1, \ldots , d,$
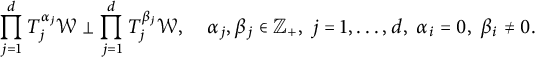 $$ \begin{align*} \prod_{{j=1}}^d T^{\alpha_j}_j \mathcal W \perp \prod_{j=1}^d T^{\beta_j}_j \mathcal W, \quad \alpha_j, \beta_j \in \mathbb Z_+, ~j=1, \ldots, d, ~\alpha_i =0, ~\beta_i \neq 0. \end{align*} $$
$$ \begin{align*} \prod_{{j=1}}^d T^{\alpha_j}_j \mathcal W \perp \prod_{j=1}^d T^{\beta_j}_j \mathcal W, \quad \alpha_j, \beta_j \in \mathbb Z_+, ~j=1, \ldots, d, ~\alpha_i =0, ~\beta_i \neq 0. \end{align*} $$
Remark 1.6 If
![]() $d=1,$
then
$d=1,$
then
![]() $\mathcal W$
is a wandering subspace for T if and only if
$\mathcal W$
is a wandering subspace for T if and only if
![]() $\mathcal W \perp T^k(\mathcal W)$
for every integer
$\mathcal W \perp T^k(\mathcal W)$
for every integer
![]() $k \geqslant 1.$
In particular,
$k \geqslant 1.$
In particular,
![]() $\ker T^*$
is a wandering subspace for any
$\ker T^*$
is a wandering subspace for any
![]() $T \in \mathcal B(\mathcal H).$
Moreover, if
$T \in \mathcal B(\mathcal H).$
Moreover, if
![]() $T=(T_1, \ldots , T_d)$
is a commuting d-tuple such that
$T=(T_1, \ldots , T_d)$
is a commuting d-tuple such that
![]() $ T^*_{j}T_{i}=T_{i}T^*_{j}, 1 \leqslant i \neq j \leqslant d,$
then
$ T^*_{j}T_{i}=T_{i}T^*_{j}, 1 \leqslant i \neq j \leqslant d,$
then
![]() $\ker T^*=\cap _{j=1}^d \ker T^*_j$
is a wandering subspace for
$\ker T^*=\cap _{j=1}^d \ker T^*_j$
is a wandering subspace for
![]() $T.$
$T.$
It follows from Remark 1.6 that the space spanned by the constant function
![]() $1$
is a wandering subspace for the multiplication
$1$
is a wandering subspace for the multiplication
![]() $2$
-tuple
$2$
-tuple
![]() $\mathscr M_z$
on
$\mathscr M_z$
on
![]() $H^2(\mathbb D^2).$
Interestingly, this fact extends to the multiplication
$H^2(\mathbb D^2).$
Interestingly, this fact extends to the multiplication
![]() $2$
-tuple
$2$
-tuple
![]() $\mathscr M_z$
on
$\mathscr M_z$
on
![]() $\mathcal D(\mu _1, \mu _2)$
(see Corollary 3.12).
$\mathcal D(\mu _1, \mu _2)$
(see Corollary 3.12).
Recall that a commuting d-tuple
![]() $T=(T_1, \ldots , T_d)$
on
$T=(T_1, \ldots , T_d)$
on
![]() $\mathcal H$
is cyclic with cyclic vector
$\mathcal H$
is cyclic with cyclic vector
![]() $f_0 \in \mathcal H$
if
$f_0 \in \mathcal H$
if
![]() $\bigvee \big \{T^{\alpha }f_0 : \alpha = (\alpha _1, \ldots , \alpha _d) \in \mathbb Z^d_+\big \}=\mathcal H,$
where
$\bigvee \big \{T^{\alpha }f_0 : \alpha = (\alpha _1, \ldots , \alpha _d) \in \mathbb Z^d_+\big \}=\mathcal H,$
where
![]() $\bigvee $
denotes the closed linear span and
$\bigvee $
denotes the closed linear span and
![]() $T^{\alpha } =\prod _{j=1}^d T^{\alpha _j}_j.$
For later purpose, we state the following property of cyclic tuples (see [Reference Albrecht, Wirtz, Helson, Sz.-Nagy, Vasilescu and Arsene3, Proposition 1.1]):
$T^{\alpha } =\prod _{j=1}^d T^{\alpha _j}_j.$
For later purpose, we state the following property of cyclic tuples (see [Reference Albrecht, Wirtz, Helson, Sz.-Nagy, Vasilescu and Arsene3, Proposition 1.1]):
where
![]() $\ker S=\cap _{j=1}^d \ker S_j$
for the d-tuple
$\ker S=\cap _{j=1}^d \ker S_j$
for the d-tuple
![]() $S=(S_1, \ldots , S_d)$
and
$S=(S_1, \ldots , S_d)$
and
![]() $\dim $
stands for the Hilbert space dimension. A commuting d-tuple T on
$\dim $
stands for the Hilbert space dimension. A commuting d-tuple T on
![]() $\mathcal H$
has the wandering subspace property if
$\mathcal H$
has the wandering subspace property if
![]() $\mathcal H=\bigvee _{\alpha \in \mathbb Z_+} T^\alpha (\ker T^*).$
Following [Reference Eschmeier and Langendörfer15, p. 56], we say that a commuting d-tuple
$\mathcal H=\bigvee _{\alpha \in \mathbb Z_+} T^\alpha (\ker T^*).$
Following [Reference Eschmeier and Langendörfer15, p. 56], we say that a commuting d-tuple
![]() $T=(T_1, \ldots , T_d)$
on
$T=(T_1, \ldots , T_d)$
on
![]() $\mathcal H$
is analytic if
$\mathcal H$
is analytic if
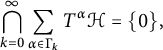 $$ \begin{align*}\bigcap_{k=0}^{\infty} \sum_{\alpha \in \Gamma_k}T^{\alpha}\mathcal H = \{0\},\end{align*} $$
$$ \begin{align*}\bigcap_{k=0}^{\infty} \sum_{\alpha \in \Gamma_k}T^{\alpha}\mathcal H = \{0\},\end{align*} $$
where, for
![]() $k \in \mathbb Z_+, \Gamma _k := \{\alpha =(\alpha _1, \ldots , \alpha _d) \in \mathbb Z^d_+: \alpha _1 + \cdots + \alpha _d = k\}.$
Note that if T is analytic, then
$k \in \mathbb Z_+, \Gamma _k := \{\alpha =(\alpha _1, \ldots , \alpha _d) \in \mathbb Z^d_+: \alpha _1 + \cdots + \alpha _d = k\}.$
Note that if T is analytic, then
![]() $T_1, \ldots , T_d$
are analytic.
$T_1, \ldots , T_d$
are analytic.
Let
![]() $\Omega $
be a domain in
$\Omega $
be a domain in
![]() $\mathbb C^d.$
For a positive integer n, let
$\mathbb C^d.$
For a positive integer n, let
![]() $\mathbf {B}_n(\Omega )$
denote the set of all commuting d-tuples T on
$\mathbf {B}_n(\Omega )$
denote the set of all commuting d-tuples T on
![]() $\mathcal H$
satisfying the following conditions:
$\mathcal H$
satisfying the following conditions:
-
• for every
 $\omega =(\omega _1, \ldots , \omega _d) \in \Omega $
, the map
$\omega =(\omega _1, \ldots , \omega _d) \in \Omega $
, the map
 $D_{T- \omega }(x) = ((T_j-\omega _j)x)_{j=1}^d$
from
$D_{T- \omega }(x) = ((T_j-\omega _j)x)_{j=1}^d$
from
 $\mathcal H$
into
$\mathcal H$
into
 $\mathcal H^{\oplus d}$
has closed range and
$\mathcal H^{\oplus d}$
has closed range and
 $\dim {\ker ({T-\omega })} = n,$
$\dim {\ker ({T-\omega })} = n,$
-
• the subspace
 $\bigvee _{\omega \in \Omega } \ker ({T-\omega })$
of
$\bigvee _{\omega \in \Omega } \ker ({T-\omega })$
of
 $\mathcal H$
equals
$\mathcal H$
equals
 $\mathcal H$
.
$\mathcal H$
.
We call the set
![]() $\mathbf {B}_n(\Omega )$
the Cowen–Douglas class of rank n with respect to
$\mathbf {B}_n(\Omega )$
the Cowen–Douglas class of rank n with respect to
![]() $\Omega $
(refer to [Reference Cowen and Douglas10, Reference Curto and Salinas13] for the basic theory of Cowen–Douglas class).
$\Omega $
(refer to [Reference Cowen and Douglas10, Reference Curto and Salinas13] for the basic theory of Cowen–Douglas class).
2 Statements of main theorems
The following three theorems collect several basic properties of Dirichlet-type spaces
![]() $\mathcal D(\mu _1, \mu _2).$
$\mathcal D(\mu _1, \mu _2).$
Theorem 2.1 For
![]() $\mu _1, \mu _2 \in M_+(\mathbb T),$
we have the following statements
$\mu _1, \mu _2 \in M_+(\mathbb T),$
we have the following statements
![]() $:$
$:$
-
(i) the coordinate functions
 $z_1, z_2$
are multipliers of
$z_1, z_2$
are multipliers of
 $\mathcal D(\mu _1, \mu _2),$
$\mathcal D(\mu _1, \mu _2),$
-
(ii) the polynomials are dense in
 $\mathcal D(\mu _1, \mu _2),$
$\mathcal D(\mu _1, \mu _2),$
-
(iii) for nonnegative integers
 $k, l$
and a polynomial p in
$k, l$
and a polynomial p in
 $z_1$
and
$z_1$
and
 $z_2,$
(2.1)
$z_2,$
(2.1) $$ \begin{align} \notag \|z^k_1z^l_2p\|^2_{\mathcal D(\mu_1, \mu_2)} &= \|p\|^2_{\mathcal D(\mu_1, \mu_2)} + k \int_{\mathbb T^2} |p(e^{i \eta}, e^{i \theta})|^2 d\mu_1(\eta)d\theta \\& \quad + l \int_{\mathbb T^2} |p(e^{i \theta}, e^{i \eta})|^2 d\mu_2(\eta)d\theta. \end{align} $$
$$ \begin{align} \notag \|z^k_1z^l_2p\|^2_{\mathcal D(\mu_1, \mu_2)} &= \|p\|^2_{\mathcal D(\mu_1, \mu_2)} + k \int_{\mathbb T^2} |p(e^{i \eta}, e^{i \theta})|^2 d\mu_1(\eta)d\theta \\& \quad + l \int_{\mathbb T^2} |p(e^{i \theta}, e^{i \eta})|^2 d\mu_2(\eta)d\theta. \end{align} $$
Theorem 2.2 For
![]() $\mu _1, \mu _2 \in M_+(\mathbb T), \mathcal D(\mu _1, \mu _2)$
has the division property.
$\mu _1, \mu _2 \in M_+(\mathbb T), \mathcal D(\mu _1, \mu _2)$
has the division property.
Theorem 2.3 For
![]() $\mu _1, \mu _2 \in M_+(\mathbb T),$
Gleason’s problem can be solved for
$\mu _1, \mu _2 \in M_+(\mathbb T),$
Gleason’s problem can be solved for
![]() $\mathcal D(\mu _1, \mu _2)$
over
$\mathcal D(\mu _1, \mu _2)$
over
![]() $\mathbb D^2_r$
for some
$\mathbb D^2_r$
for some
![]() $r \in (0, 1].$
$r \in (0, 1].$
Here
![]() $\mathbb D^2_r$
denotes the bidisc
$\mathbb D^2_r$
denotes the bidisc
![]() $\{(z_1, z_2) \in \mathbb C^2 : |z_1|< r, \,|z_2|< r\},$
where r is a positive real number. Unlike the one variable situation, we do not know whether Gleason’s problem can be solved for
$\{(z_1, z_2) \in \mathbb C^2 : |z_1|< r, \,|z_2|< r\},$
where r is a positive real number. Unlike the one variable situation, we do not know whether Gleason’s problem can be solved for
![]() $\mathcal D(\mu _1, \mu _2)$
over the unit bidisc. It is worth noting that not all facts about Dirichlet-type spaces of the unit disc have successful counterparts in the bidisc case. For example, the commuting pair
$\mathcal D(\mu _1, \mu _2)$
over the unit bidisc. It is worth noting that not all facts about Dirichlet-type spaces of the unit disc have successful counterparts in the bidisc case. For example, the commuting pair
![]() $\mathscr M_z=(\mathscr M_{z_1}, \mathscr M_{z_2})$
on
$\mathscr M_z=(\mathscr M_{z_1}, \mathscr M_{z_2})$
on
![]() $\mathcal D(\mu _1, \mu _2)$
fails to be essentially normal (see Corollary 3.13). Moreover, the verbatim analog of the model theorem [Reference Richter26, Theorem 5.1] does not hold true (see Remark 2.5).
$\mathcal D(\mu _1, \mu _2)$
fails to be essentially normal (see Corollary 3.13). Moreover, the verbatim analog of the model theorem [Reference Richter26, Theorem 5.1] does not hold true (see Remark 2.5).
The following result asserts that
![]() $\mathscr M_z$
on
$\mathscr M_z$
on
![]() $\mathcal D(\mu _1, \mu _2)$
is a canonical model for analytic
$\mathcal D(\mu _1, \mu _2)$
is a canonical model for analytic
![]() $2$
-isometries T for which
$2$
-isometries T for which
![]() $\ker T^*$
is a cyclic wandering subspace.
$\ker T^*$
is a cyclic wandering subspace.
Theorem 2.4 (A representation theorem)
Let
![]() $T=(T_1, T_2)$
be a commuting pair on
$T=(T_1, T_2)$
be a commuting pair on
![]() $\mathcal H.$
Then the following statements are equivalent:
$\mathcal H.$
Then the following statements are equivalent:
-
(i) T is a cyclic analytic toral
 $2$
-isometry with cyclic vector
$2$
-isometry with cyclic vector
 $f_0 \in \ker T^*$
and
$f_0 \in \ker T^*$
and
 $\ker T^*$
is a wandering subspace for
$\ker T^*$
is a wandering subspace for
 $T,$
$T,$
-
(ii) T is a cyclic toral
 $2$
-isometry with cyclic vector
$2$
-isometry with cyclic vector
 $f_0 \in \ker T^*$
,
$f_0 \in \ker T^*$
,
 $T^*$
belongs to
$T^*$
belongs to
 $\mathbf {B}_1(\mathbb D^2_r)$
for some
$\mathbf {B}_1(\mathbb D^2_r)$
for some
 $r \in (0, 1]$
and
$r \in (0, 1]$
and
 $\ker T^*$
is a wandering subspace for
$\ker T^*$
is a wandering subspace for
 $T,$
$T,$
-
(iii) there exist
 $\mu _1, \mu _2 \in M_+(\mathbb T)$
such that T is unitarily equivalent to
$\mu _1, \mu _2 \in M_+(\mathbb T)$
such that T is unitarily equivalent to
 $\mathscr M_z$
on
$\mathscr M_z$
on
 $\mathcal D(\mu _1, \mu _2).$
$\mathcal D(\mu _1, \mu _2).$
Remark 2.5 By [Reference Richter25, Theorem 1], any analytic
![]() $2$
-isometry T on
$2$
-isometry T on
![]() $\mathcal H$
has the wandering subspace property. This result fails even for analytic toral isometric d-tuples if
$\mathcal H$
has the wandering subspace property. This result fails even for analytic toral isometric d-tuples if
![]() $d> 1.$
Indeed, if
$d> 1.$
Indeed, if
![]() $a \in \mathbb D^2 \backslash \{(0, 0)\},$
then the restriction of
$a \in \mathbb D^2 \backslash \{(0, 0)\},$
then the restriction of
![]() $\mathscr M_z$
to
$\mathscr M_z$
to
![]() $\{f \in H^2(\mathbb D^2) : f(a)=0\}$
is a toral isometry without the wandering subspace property. This may be seen by imitating the argument of [Reference Bhattacharjee, Eschmeier, Keshari and Sarkar6, Example 6.8] with the only change that the application of [Reference Gleason, Richter and Sundberg19, Theorem 4.3] is replaced by that of [Reference Gleason, Richter and Sundberg19, Corollary 4.6]. This example also shows that the assumption that the cyclic vector
$\{f \in H^2(\mathbb D^2) : f(a)=0\}$
is a toral isometry without the wandering subspace property. This may be seen by imitating the argument of [Reference Bhattacharjee, Eschmeier, Keshari and Sarkar6, Example 6.8] with the only change that the application of [Reference Gleason, Richter and Sundberg19, Theorem 4.3] is replaced by that of [Reference Gleason, Richter and Sundberg19, Corollary 4.6]. This example also shows that the assumption that the cyclic vector
![]() $f_0$
belongs to
$f_0$
belongs to
![]() $\ker T^*$
in (i) can not be dropped from Theorem 2.4. Also, by Theorem 2.1(ii), the cyclicity of T in (ii) of Theorem 2.4 can not be relaxed.
$\ker T^*$
in (i) can not be dropped from Theorem 2.4. Also, by Theorem 2.1(ii), the cyclicity of T in (ii) of Theorem 2.4 can not be relaxed.
Theorems 2.1, 2.3, and 2.4 provide bidisc analogs of [Reference Richter26, Theorems 3.6, 3.7, and 5.1], respectively. Also, Theorem 2.2 presents a counterpart of the fact that Dirichlet-type spaces on the unit disc have the division property (see [Reference Richter26, Corollary 3.8] and [Reference Richter24, Lemma 2.1]). The proofs of these results and their consequences are presented in Sections 3–6 (see Corollaries 3.8, 3.9, 3.12, 3.13, 4.6, 5.5, 5.6, 6.2, 6.6). In the final short section, we discuss the spectral picture of the multiplication
![]() $2$
-tuple
$2$
-tuple
![]() $\mathscr M_z$
on
$\mathscr M_z$
on
![]() $\mathcal D(\mu _1, \mu _2)$
and raise some related questions.
$\mathcal D(\mu _1, \mu _2)$
and raise some related questions.
3 Proof of Theorem 2.1 and its consequences
We need several lemmas to prove Theorem 2.1.
Lemma 3.1 The Dirichlet-type space
![]() $\mathcal D(\mu _1, \mu _2)$
is a reproducing kernel Hilbert space. If
$\mathcal D(\mu _1, \mu _2)$
is a reproducing kernel Hilbert space. If
![]() $\kappa : \mathbb D \times \mathbb D \rightarrow \mathbb C$
is the reproducing kernel of
$\kappa : \mathbb D \times \mathbb D \rightarrow \mathbb C$
is the reproducing kernel of
![]() $\mathcal D(\mu _1, \mu _2),$
then for any
$\mathcal D(\mu _1, \mu _2),$
then for any
![]() $r \in (0, 1), \bigvee \{\kappa (\cdot , w) : |w| < r\}=\mathcal D(\mu _1, \mu _2)$
and
$r \in (0, 1), \bigvee \{\kappa (\cdot , w) : |w| < r\}=\mathcal D(\mu _1, \mu _2)$
and
![]() $\kappa (\cdot , 0)=1.$
$\kappa (\cdot , 0)=1.$
Proof We borrow an argument from the proof of [Reference El-Fallah, Kellay, Mashreghi and Ransford14, Theorem 1.6.3]. Let
![]() $\{f_n\}_{n \geqslant 0}$
be a Cauchy sequence in
$\{f_n\}_{n \geqslant 0}$
be a Cauchy sequence in
![]() $\mathcal D(\mu _1, \mu _2).$
Since
$\mathcal D(\mu _1, \mu _2).$
Since
![]() $H^2(\mathbb D^2)$
is complete (see [Reference Rudin27, p. 53]), there exists a
$H^2(\mathbb D^2)$
is complete (see [Reference Rudin27, p. 53]), there exists a
![]() $f \in H^2(\mathbb D^2)$
such that
$f \in H^2(\mathbb D^2)$
such that
![]() $\|f_n-f\|^2_{H^2(\mathbb D^2)} \rightarrow 0$
as
$\|f_n-f\|^2_{H^2(\mathbb D^2)} \rightarrow 0$
as
![]() $n \rightarrow \infty .$
Moreover, since
$n \rightarrow \infty .$
Moreover, since
![]() $H^2(\mathbb D^2)$
is a reproducing kernel Hilbert space, for every
$H^2(\mathbb D^2)$
is a reproducing kernel Hilbert space, for every
![]() $j=1, 2, \partial _j f_n$
converges compactly to
$j=1, 2, \partial _j f_n$
converges compactly to
![]() $\partial _j f$
on
$\partial _j f$
on
![]() $\mathbb D^2.$
Also, since
$\mathbb D^2.$
Also, since
![]() $\{f_n\}_{n \geqslant 0}$
is bounded in
$\{f_n\}_{n \geqslant 0}$
is bounded in
![]() $\mathcal D(\mu _1, \mu _2)$
, by Lemma 1.1, there exists an
$\mathcal D(\mu _1, \mu _2)$
, by Lemma 1.1, there exists an
![]() $M> 0$
such that for every integer
$M> 0$
such that for every integer
![]() $n \geqslant 0$
and
$n \geqslant 0$
and
![]() $r \in (0, 1),$
$r \in (0, 1),$
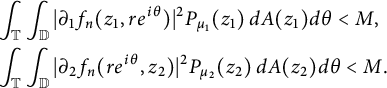 $$ \begin{align*} & \int_{\mathbb T} \int_{\mathbb D}|\partial_1 f_n(z_1, re^{i \theta})|^2 P_{\mu_1}(z_1) \,dA(z_1)d\theta < M, \\ & \int_{\mathbb T} \int_{\mathbb D}|\partial_2 f_n(re^{i \theta}, z_2)|^2 P_{\mu_2}(z_2) \,dA(z_2)d\theta < M. \end{align*} $$
$$ \begin{align*} & \int_{\mathbb T} \int_{\mathbb D}|\partial_1 f_n(z_1, re^{i \theta})|^2 P_{\mu_1}(z_1) \,dA(z_1)d\theta < M, \\ & \int_{\mathbb T} \int_{\mathbb D}|\partial_2 f_n(re^{i \theta}, z_2)|^2 P_{\mu_2}(z_2) \,dA(z_2)d\theta < M. \end{align*} $$
By Fatou’s lemma (see [Reference Rudin28, Lemma 1.28]), for any
![]() $r \in (0, 1),$
$r \in (0, 1),$
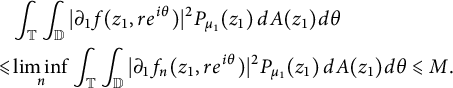 $$ \begin{align} & \int_{\mathbb T} \int_{\mathbb D}|\partial_1 f(z_1, re^{i \theta})|^2 P_{\mu_1}(z_1) \,dA(z_1)d\theta \\ \leqslant & \liminf_n \int_{\mathbb T} \int_{\mathbb D}|\partial_1 f_n(z_1, re^{i \theta})|^2 P_{\mu_1}(z_1) \,dA(z_1)d\theta \leqslant M. \notag \end{align} $$
$$ \begin{align} & \int_{\mathbb T} \int_{\mathbb D}|\partial_1 f(z_1, re^{i \theta})|^2 P_{\mu_1}(z_1) \,dA(z_1)d\theta \\ \leqslant & \liminf_n \int_{\mathbb T} \int_{\mathbb D}|\partial_1 f_n(z_1, re^{i \theta})|^2 P_{\mu_1}(z_1) \,dA(z_1)d\theta \leqslant M. \notag \end{align} $$
Similarly, one can see that
This shows that
![]() $f \in \mathcal D(\mu _1, \mu _2).$
We may now argue as in (3.1) (with f replaced by
$f \in \mathcal D(\mu _1, \mu _2).$
We may now argue as in (3.1) (with f replaced by
![]() $f_n-f$
and
$f_n-f$
and
![]() $f_n$
replaced by
$f_n$
replaced by
![]() $f_n-f_m$
) and use Fatou’s lemma to conclude that
$f_n-f_m$
) and use Fatou’s lemma to conclude that
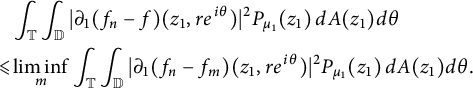 $$ \begin{align*} & \int_{\mathbb T} \int_{\mathbb D}|\partial_1 (f_n-f)(z_1, re^{i \theta})|^2 P_{\mu_1}(z_1) \,dA(z_1)d\theta \\ \leqslant & \liminf_m \int_{\mathbb T} \int_{\mathbb D}|\partial_1 (f_n-f_m)(z_1, re^{i \theta})|^2 P_{\mu_1}(z_1) \,dA(z_1)d\theta. \end{align*} $$
$$ \begin{align*} & \int_{\mathbb T} \int_{\mathbb D}|\partial_1 (f_n-f)(z_1, re^{i \theta})|^2 P_{\mu_1}(z_1) \,dA(z_1)d\theta \\ \leqslant & \liminf_m \int_{\mathbb T} \int_{\mathbb D}|\partial_1 (f_n-f_m)(z_1, re^{i \theta})|^2 P_{\mu_1}(z_1) \,dA(z_1)d\theta. \end{align*} $$
Similarly, we obtain
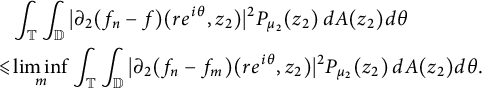 $$ \begin{align*} & \int_{\mathbb T} \int_{\mathbb D}|\partial_2 (f_n-f)(re^{i \theta}, z_2)|^2 P_{\mu_2}(z_2) \,dA(z_2)d\theta \\ \leqslant & \liminf_m \int_{\mathbb T} \int_{\mathbb D}|\partial_2 (f_n-f_m)(re^{i \theta}, z_2)|^2 P_{\mu_2}(z_2) \,dA(z_2)d\theta. \end{align*} $$
$$ \begin{align*} & \int_{\mathbb T} \int_{\mathbb D}|\partial_2 (f_n-f)(re^{i \theta}, z_2)|^2 P_{\mu_2}(z_2) \,dA(z_2)d\theta \\ \leqslant & \liminf_m \int_{\mathbb T} \int_{\mathbb D}|\partial_2 (f_n-f_m)(re^{i \theta}, z_2)|^2 P_{\mu_2}(z_2) \,dA(z_2)d\theta. \end{align*} $$
These two estimates combined with Lemma 1.1 yield
This shows that
![]() $\{f_n\}_{n \geqslant 0}$
converges to f in
$\{f_n\}_{n \geqslant 0}$
converges to f in
![]() $\mathcal D(\mu _1, \mu _2).$
Finally, since
$\mathcal D(\mu _1, \mu _2).$
Finally, since
![]() $H^2(\mathbb D^2)$
is a reproducing kernel Hilbert space, so is
$H^2(\mathbb D^2)$
is a reproducing kernel Hilbert space, so is
![]() $\mathcal D(\mu _1, \mu _2)$
(see Lemma 1.3).
$\mathcal D(\mu _1, \mu _2)$
(see Lemma 1.3).
To see the “moreover” part, note that for any
![]() $f \in \mathcal D(\mu _1, \mu _2),$
by the reproducing property of
$f \in \mathcal D(\mu _1, \mu _2),$
by the reproducing property of
![]() $\mathcal D(\mu _1, \mu _2),$
$\mathcal D(\mu _1, \mu _2),$
and hence
![]() $\kappa (\cdot , 0)=1.$
The rest follows from the reproducing property of
$\kappa (\cdot , 0)=1.$
The rest follows from the reproducing property of
![]() $\mathcal D(\mu _1, \mu _2)$
together with an application of the identity theorem.
$\mathcal D(\mu _1, \mu _2)$
together with an application of the identity theorem.
Although we do not need in this section, the full strength of the following lemma (cf. [Reference Gleason and Richter18, Theorem 4.2]), we include it for later usage.
Lemma 3.2 Let
![]() $f : \mathbb D^2 \rightarrow \mathbb C$
be a holomorphic function. For
$f : \mathbb D^2 \rightarrow \mathbb C$
be a holomorphic function. For
![]() $r \in (0, 1)$
and
$r \in (0, 1)$
and
![]() $\theta \in [0, 2\pi ],$
consider the holomorphic function
$\theta \in [0, 2\pi ],$
consider the holomorphic function
![]() $f_{r, \theta }(w)=f(w, re^{i \theta }), w \in \mathbb D.$
If
$f_{r, \theta }(w)=f(w, re^{i \theta }), w \in \mathbb D.$
If
![]() $f \in H^2(\mathbb D^2),$
then
$f \in H^2(\mathbb D^2),$
then
![]() $f_{r, \theta } \in H^2(\mathbb D)$
for every
$f_{r, \theta } \in H^2(\mathbb D)$
for every
![]() $r \in (0, 1)$
and
$r \in (0, 1)$
and
![]() $\theta \in [0, 2\pi ].$
Moreover,
$\theta \in [0, 2\pi ].$
Moreover,
Proof The proof relies on the formula (1.3). First, note that
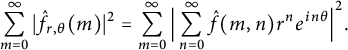 $$ \begin{align} \sum_{m =0}^{\infty} |\hat{f}_{r, \theta}(m)|^2 = \sum_{m=0}^{\infty} \Big|\sum_{n=0}^{\infty} \hat{f}(m, n) r^n e^{in \theta}\Big|^2. \end{align} $$
$$ \begin{align} \sum_{m =0}^{\infty} |\hat{f}_{r, \theta}(m)|^2 = \sum_{m=0}^{\infty} \Big|\sum_{n=0}^{\infty} \hat{f}(m, n) r^n e^{in \theta}\Big|^2. \end{align} $$
If
![]() $f \in H^2(\mathbb D^2),$
then applying the Cauchy–Schwarz inequality to (3.3) gives that
$f \in H^2(\mathbb D^2),$
then applying the Cauchy–Schwarz inequality to (3.3) gives that
![]() ${f_{r, \theta } \in H^2(\mathbb D)}$
for every
${f_{r, \theta } \in H^2(\mathbb D)}$
for every
![]() $r \in (0, 1)$
and
$r \in (0, 1)$
and
![]() $\theta \in [0, 2\pi ].$
Moreover, integrating both sides of (3.3) with respect to
$\theta \in [0, 2\pi ].$
Moreover, integrating both sides of (3.3) with respect to
![]() $\theta $
over
$\theta $
over
![]() $[0, 2\pi ]$
and taking supremum over
$[0, 2\pi ]$
and taking supremum over
![]() $r \in (0, 1)$
yields (3.2).
$r \in (0, 1)$
yields (3.2).
Remark 3.3 We note that
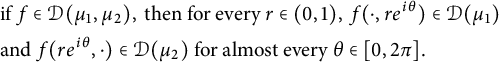 $$ \begin{align} \notag &\text{if } f \in \mathcal D(\mu_1, \mu_2), \text{ then for every } r \in (0, 1), \, f(\cdot, re^{i\theta}) \in \mathcal D(\mu_1) \\&\text{and } f(re^{i\theta}, \cdot) \in \mathcal D(\mu_2) \text{ for almost every } \theta \in [0, 2\pi]. \end{align} $$
$$ \begin{align} \notag &\text{if } f \in \mathcal D(\mu_1, \mu_2), \text{ then for every } r \in (0, 1), \, f(\cdot, re^{i\theta}) \in \mathcal D(\mu_1) \\&\text{and } f(re^{i\theta}, \cdot) \in \mathcal D(\mu_2) \text{ for almost every } \theta \in [0, 2\pi]. \end{align} $$
To see this, note that for any holomorphic function
![]() $f : \mathbb D^2 \rightarrow \mathbb C,$
$f : \mathbb D^2 \rightarrow \mathbb C,$
and hence, if
![]() $f \in \mathcal D(\mu _1, \mu _2),$
then by Lemma 1.1,
$f \in \mathcal D(\mu _1, \mu _2),$
then by Lemma 1.1,
![]() $\int _{\mathbb T} D_{\mu _1}(f(\cdot , re^{i\theta })) d\theta $
and
$\int _{\mathbb T} D_{\mu _1}(f(\cdot , re^{i\theta })) d\theta $
and
![]() $\int _{\mathbb T} D_{\mu _2}(f(re^{i\theta }, \cdot ))d\theta $
are finite for every
$\int _{\mathbb T} D_{\mu _2}(f(re^{i\theta }, \cdot ))d\theta $
are finite for every
![]() $r \in (0, 1).$
One may now apply Lemma 3.2 to complete the verification of (3.4).
$r \in (0, 1).$
One may now apply Lemma 3.2 to complete the verification of (3.4).
It turns out that the operator
![]() $\mathscr M_{z_j}$
of multiplication by the coordinate functions
$\mathscr M_{z_j}$
of multiplication by the coordinate functions
![]() $z_j, j=1, 2,$
defines a bounded linear operator on
$z_j, j=1, 2,$
defines a bounded linear operator on
![]() $\mathcal D(\mu _1, \mu _2).$
$\mathcal D(\mu _1, \mu _2).$
Lemma 3.4 The coordinate functions
![]() $z_1, z_2$
are multipliers of
$z_1, z_2$
are multipliers of
![]() $\mathcal D(\mu _1, \mu _2).$
$\mathcal D(\mu _1, \mu _2).$
Proof By (3.4), for any
![]() $f \in \mathcal D(\mu _1, \mu _2)$
and
$f \in \mathcal D(\mu _1, \mu _2)$
and
![]() $r \in (0, 1), f(\cdot , re^{i \theta }) \in \mathcal D(\mu _1)$
for a.e.
$r \in (0, 1), f(\cdot , re^{i \theta }) \in \mathcal D(\mu _1)$
for a.e.
![]() $\theta \in [0,2\pi ].$
By [Reference Richter26, Theorem 3.6], the operator
$\theta \in [0,2\pi ].$
By [Reference Richter26, Theorem 3.6], the operator
![]() $\mathscr M_w$
of multiplication by the coordinate function w on
$\mathscr M_w$
of multiplication by the coordinate function w on
![]() $\mathcal D(\mu _1)$
is bounded and satisfies
$\mathcal D(\mu _1)$
is bounded and satisfies
Since
![]() $\mathscr M^*_w\mathscr M_w \geqslant I, \|\mathscr M_w\| \geqslant 1.$
Fix now
$\mathscr M^*_w\mathscr M_w \geqslant I, \|\mathscr M_w\| \geqslant 1.$
Fix now
![]() $f \in \mathcal D(\mu _1, \mu _2).$
By Lemma 1.3,
$f \in \mathcal D(\mu _1, \mu _2).$
By Lemma 1.3,
![]() $f \in H^2(\mathbb D^2),$
and hence
$f \in H^2(\mathbb D^2),$
and hence
![]() $z_1f \in H^2(\mathbb D^2).$
By (3.5) (two applications),
$z_1f \in H^2(\mathbb D^2).$
By (3.5) (two applications),
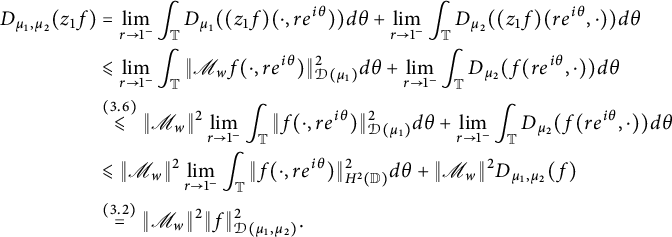 $$ \begin{align*} D_{\mu_1, \mu_2}(z_1f) &= \lim_{r \rightarrow 1^{-}} \int_{\mathbb T} D_{\mu_1}((z_1f)(\cdot, re^{i\theta}))d\theta + \lim_{r \rightarrow 1^{-}} \int_{\mathbb T} D_{\mu_2}((z_1f)(re^{i\theta}, \cdot))d\theta \\ &\leqslant \lim_{r \rightarrow 1^{-}} \int_{\mathbb T}\|\mathscr M_w f(\cdot, re^{i \theta})\|^2_{\mathcal D(\mu_1)} d\theta + \lim_{r \rightarrow 1^{-}} \int_{\mathbb T} D_{\mu_2}(f(re^{i\theta}, \cdot))d\theta \\ & \overset{({3.6})}\leqslant \|\mathscr M_w\|^2 \lim_{r \rightarrow 1^{-}} \int_{\mathbb T}\|f(\cdot, re^{i \theta})\|^2_{\mathcal D(\mu_1)} d\theta + \lim_{r \rightarrow 1^{-}} \int_{\mathbb T} D_{\mu_2}(f(re^{i\theta}, \cdot))d\theta \\ & \leqslant \|\mathscr M_w\|^2 \lim_{r \rightarrow 1^{-}} \int_{\mathbb T}\|f(\cdot, re^{i \theta})\|^2_{H^2(\mathbb D)} d\theta + \|\mathscr M_w\|^2 D_{\mu_1, \mu_2}(f)\\ &\overset{({3.2})}= \|\mathscr M_w\|^2 \|f\|^2_{\mathcal D(\mu_1, \mu_2)}. \end{align*} $$
$$ \begin{align*} D_{\mu_1, \mu_2}(z_1f) &= \lim_{r \rightarrow 1^{-}} \int_{\mathbb T} D_{\mu_1}((z_1f)(\cdot, re^{i\theta}))d\theta + \lim_{r \rightarrow 1^{-}} \int_{\mathbb T} D_{\mu_2}((z_1f)(re^{i\theta}, \cdot))d\theta \\ &\leqslant \lim_{r \rightarrow 1^{-}} \int_{\mathbb T}\|\mathscr M_w f(\cdot, re^{i \theta})\|^2_{\mathcal D(\mu_1)} d\theta + \lim_{r \rightarrow 1^{-}} \int_{\mathbb T} D_{\mu_2}(f(re^{i\theta}, \cdot))d\theta \\ & \overset{({3.6})}\leqslant \|\mathscr M_w\|^2 \lim_{r \rightarrow 1^{-}} \int_{\mathbb T}\|f(\cdot, re^{i \theta})\|^2_{\mathcal D(\mu_1)} d\theta + \lim_{r \rightarrow 1^{-}} \int_{\mathbb T} D_{\mu_2}(f(re^{i\theta}, \cdot))d\theta \\ & \leqslant \|\mathscr M_w\|^2 \lim_{r \rightarrow 1^{-}} \int_{\mathbb T}\|f(\cdot, re^{i \theta})\|^2_{H^2(\mathbb D)} d\theta + \|\mathscr M_w\|^2 D_{\mu_1, \mu_2}(f)\\ &\overset{({3.2})}= \|\mathscr M_w\|^2 \|f\|^2_{\mathcal D(\mu_1, \mu_2)}. \end{align*} $$
Similarly, one can see that for some
![]() $c_2 \geqslant 1,$
$c_2 \geqslant 1,$
This completes the proof.
The following is a bidisc analog of Richter’s formula (see [Reference Richter26, proof of Theorem 4.1], [Reference Chavan, Gupta and Reza8, Theorem 1.3]).
Lemma 3.5 For nonnegative integers
![]() $k, l$
and a polynomial p in the complex variables
$k, l$
and a polynomial p in the complex variables
![]() $z_1$
and
$z_1$
and
![]() $z_2,$
we have the formula (2.1).
$z_2,$
we have the formula (2.1).
Proof By (3.4) (see also (3.5)) and [Reference Richter26, proof of Theorem 4.1],
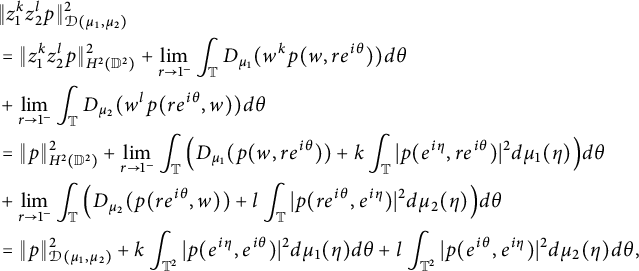 $$ \begin{align*} & \|z^k_1z^l_2p\|^2_{\mathcal D(\mu_1, \mu_2)} \\ &= \|z^k_1z^l_2 p\|^2_{H^2(\mathbb D^2)} +\lim_{r \rightarrow 1^{-}} \int_{\mathbb T} D_{\mu_1}( w^k p(w, re^{i \theta}))d\theta \\ &+ \lim_{r \rightarrow 1^{-}} \int_{\mathbb T} D_{\mu_2}( w^l p(re^{i \theta}, w))d\theta \\ &= \|p\|^2_{H^2(\mathbb D^2)} + \lim_{r \rightarrow 1^{-}} \int_{\mathbb T} \Big(D_{\mu_1}(p(w, re^{i \theta}))+ k \int_{\mathbb T} |p(e^{i \eta}, r e^{i \theta})|^2 d\mu_1(\eta)\Big)d\theta \\ &+ \lim_{r \rightarrow 1^{-}} \int_{\mathbb T} \Big(D_{\mu_2}(p(re^{i \theta}, w))+ l \int_{\mathbb T} |p(r e^{i \theta}, e^{i \eta})|^2 d\mu_2(\eta)\Big)d\theta \\ &= \|p\|^2_{\mathcal D(\mu_1, \mu_2)} + k \int_{\mathbb T^2} |p(e^{i \eta}, e^{i \theta})|^2 d\mu_1(\eta)d\theta + l \int_{\mathbb T^2} |p(e^{i \theta}, e^{i \eta})|^2 d\mu_2(\eta)d\theta, \end{align*} $$
$$ \begin{align*} & \|z^k_1z^l_2p\|^2_{\mathcal D(\mu_1, \mu_2)} \\ &= \|z^k_1z^l_2 p\|^2_{H^2(\mathbb D^2)} +\lim_{r \rightarrow 1^{-}} \int_{\mathbb T} D_{\mu_1}( w^k p(w, re^{i \theta}))d\theta \\ &+ \lim_{r \rightarrow 1^{-}} \int_{\mathbb T} D_{\mu_2}( w^l p(re^{i \theta}, w))d\theta \\ &= \|p\|^2_{H^2(\mathbb D^2)} + \lim_{r \rightarrow 1^{-}} \int_{\mathbb T} \Big(D_{\mu_1}(p(w, re^{i \theta}))+ k \int_{\mathbb T} |p(e^{i \eta}, r e^{i \theta})|^2 d\mu_1(\eta)\Big)d\theta \\ &+ \lim_{r \rightarrow 1^{-}} \int_{\mathbb T} \Big(D_{\mu_2}(p(re^{i \theta}, w))+ l \int_{\mathbb T} |p(r e^{i \theta}, e^{i \eta})|^2 d\mu_2(\eta)\Big)d\theta \\ &= \|p\|^2_{\mathcal D(\mu_1, \mu_2)} + k \int_{\mathbb T^2} |p(e^{i \eta}, e^{i \theta})|^2 d\mu_1(\eta)d\theta + l \int_{\mathbb T^2} |p(e^{i \theta}, e^{i \eta})|^2 d\mu_2(\eta)d\theta, \end{align*} $$
where we used Lemma 1.1 and the monotone convergence theorem.
For
![]() $R=(R_1, R_2) \in (0, 1)^2$
and
$R=(R_1, R_2) \in (0, 1)^2$
and
![]() $f \in \mathcal O(\mathbb D^2),$
let
$f \in \mathcal O(\mathbb D^2),$
let
![]() $f_R(z)=f(R_1z_1, R_2z_2).$
To get the polynomial density in
$f_R(z)=f(R_1z_1, R_2z_2).$
To get the polynomial density in
![]() $\mathcal D(\mu _1, \mu _2),$
we need the following inequality.
$\mathcal D(\mu _1, \mu _2),$
we need the following inequality.
Lemma 3.6 For any
![]() $R=(R_1, R_2) \in (0, 1)^2$
and
$R=(R_1, R_2) \in (0, 1)^2$
and
![]() $f \in \mathcal D(\mu _1, \mu _2),$
$f \in \mathcal D(\mu _1, \mu _2),$
Proof By (3.5) and [Reference Sarason29, Proposition 3],
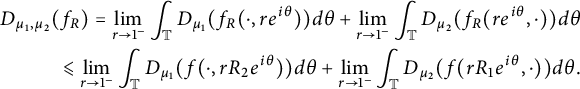 $$ \begin{align*} D_{\mu_1, \mu_2}(f_R) = \lim_{r \rightarrow 1^{-}} \int_{\mathbb T} D_{\mu_1}(f_R(\cdot, re^{i\theta})) d\theta + \lim_{r \rightarrow 1^{-}} \int_{\mathbb T} D_{\mu_2}(f_R(re^{i\theta}, \cdot))d\theta \\ \leqslant \lim_{r \rightarrow 1^{-}} \int_{\mathbb T} D_{\mu_1}(f(\cdot, rR_2e^{i\theta})) d\theta + \lim_{r \rightarrow 1^{-}} \int_{\mathbb T} D_{\mu_2}(f(rR_1e^{i\theta}, \cdot))d\theta. \end{align*} $$
$$ \begin{align*} D_{\mu_1, \mu_2}(f_R) = \lim_{r \rightarrow 1^{-}} \int_{\mathbb T} D_{\mu_1}(f_R(\cdot, re^{i\theta})) d\theta + \lim_{r \rightarrow 1^{-}} \int_{\mathbb T} D_{\mu_2}(f_R(re^{i\theta}, \cdot))d\theta \\ \leqslant \lim_{r \rightarrow 1^{-}} \int_{\mathbb T} D_{\mu_1}(f(\cdot, rR_2e^{i\theta})) d\theta + \lim_{r \rightarrow 1^{-}} \int_{\mathbb T} D_{\mu_2}(f(rR_1e^{i\theta}, \cdot))d\theta. \end{align*} $$
This, combined with Lemma 1.1, yields
An application of (3.5) now completes the proof.
Here is a key step in deducing the density of polynomials in
![]() $\mathcal D(\mu _1, \mu _2).$
$\mathcal D(\mu _1, \mu _2).$
Lemma 3.7 For any
![]() $f \in \mathcal D(\mu _1, \mu _2),$
$f \in \mathcal D(\mu _1, \mu _2),$
Proof The proof is an adaptation of that of [Reference El-Fallah, Kellay, Mashreghi and Ransford14, Theorem 7.3.1] to the present situation. For
![]() $R=(R_1, R_2) \in (0, 1)^2,$
by the Parallelogram law (which holds for any seminorm) and Lemma 3.6,
$R=(R_1, R_2) \in (0, 1)^2,$
by the Parallelogram law (which holds for any seminorm) and Lemma 3.6,
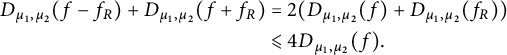 $$ \begin{align} D_{\mu_1, \mu_2}(f-f_{R}) + D_{\mu_1, \mu_2}(f+f_{R}) &= 2(D_{\mu_1, \mu_2}(f) + D_{\mu_1, \mu_2}(f_{R})) \notag \\ & \leqslant 4D_{\mu_1, \mu_2}(f). \end{align} $$
$$ \begin{align} D_{\mu_1, \mu_2}(f-f_{R}) + D_{\mu_1, \mu_2}(f+f_{R}) &= 2(D_{\mu_1, \mu_2}(f) + D_{\mu_1, \mu_2}(f_{R})) \notag \\ & \leqslant 4D_{\mu_1, \mu_2}(f). \end{align} $$
We claim that
To see this, fix
![]() $r \in (0, 1).$
By Fatou’s lemma,
$r \in (0, 1).$
By Fatou’s lemma,
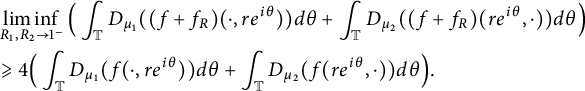 $$ \begin{align} & \liminf_{R_1, R_2 \rightarrow 1^{-}} \Big(\int_{\mathbb T} D_{\mu_1}((f+f_R)(\cdot, re^{i\theta})) d\theta + \int_{\mathbb T} D_{\mu_2}((f+f_R)(re^{i\theta}, \cdot))d\theta\Big) \notag \\ & \geqslant 4\Big(\int_{\mathbb T} D_{\mu_1}(f(\cdot, re^{i\theta})) d\theta + \int_{\mathbb T} D_{\mu_2}(f(re^{i\theta}, \cdot))d\theta\Big). \end{align} $$
$$ \begin{align} & \liminf_{R_1, R_2 \rightarrow 1^{-}} \Big(\int_{\mathbb T} D_{\mu_1}((f+f_R)(\cdot, re^{i\theta})) d\theta + \int_{\mathbb T} D_{\mu_2}((f+f_R)(re^{i\theta}, \cdot))d\theta\Big) \notag \\ & \geqslant 4\Big(\int_{\mathbb T} D_{\mu_1}(f(\cdot, re^{i\theta})) d\theta + \int_{\mathbb T} D_{\mu_2}(f(re^{i\theta}, \cdot))d\theta\Big). \end{align} $$
On the other hand, by Lemma 1.1,
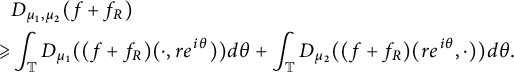 $$ \begin{align*} & D_{\mu_1, \mu_2}(f+f_{R}) \\ \geqslant & \int_{\mathbb T} D_{\mu_1}((f+f_R)(\cdot, re^{i\theta})) d\theta + \int_{\mathbb T} D_{\mu_2}((f+f_R)(re^{i\theta}, \cdot))d\theta. \end{align*} $$
$$ \begin{align*} & D_{\mu_1, \mu_2}(f+f_{R}) \\ \geqslant & \int_{\mathbb T} D_{\mu_1}((f+f_R)(\cdot, re^{i\theta})) d\theta + \int_{\mathbb T} D_{\mu_2}((f+f_R)(re^{i\theta}, \cdot))d\theta. \end{align*} $$
After taking
![]() $\liminf $
on both sides (one by one) and applying (3.9), we get
$\liminf $
on both sides (one by one) and applying (3.9), we get
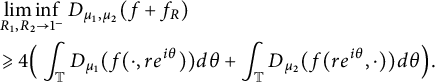 $$ \begin{align*} & \liminf_{R_1, R_2 \rightarrow 1^{-}} D_{\mu_1, \mu_2}(f+f_{R}) \\ & \geqslant 4\Big(\int_{\mathbb T} D_{\mu_1}(f(\cdot, re^{i\theta})) d\theta + \int_{\mathbb T} D_{\mu_2}(f(re^{i\theta}, \cdot))d\theta\Big). \end{align*} $$
$$ \begin{align*} & \liminf_{R_1, R_2 \rightarrow 1^{-}} D_{\mu_1, \mu_2}(f+f_{R}) \\ & \geqslant 4\Big(\int_{\mathbb T} D_{\mu_1}(f(\cdot, re^{i\theta})) d\theta + \int_{\mathbb T} D_{\mu_2}(f(re^{i\theta}, \cdot))d\theta\Big). \end{align*} $$
Letting
![]() $r \rightarrow 1^{-}$
on the right-hand side now yields (3.8) (see (3.5)). Finally, note that by (3.7),
$r \rightarrow 1^{-}$
on the right-hand side now yields (3.8) (see (3.5)). Finally, note that by (3.7),
and hence by (3.8), we get
which completes the proof.
We now complete the proof of Theorem 2.1.
Proof (Proof of Theorem 2.1)
Parts (i) and (iii) are Lemmas 3.4 and 3.5, respectively. To see (ii), let
![]() $f \in \mathcal D(\mu _1, \mu _2)$
and
$f \in \mathcal D(\mu _1, \mu _2)$
and
![]() $\epsilon>0.$
It suffices to check that there exists a polynomial p in
$\epsilon>0.$
It suffices to check that there exists a polynomial p in
![]() $z_1$
and
$z_1$
and
![]() $z_2$
such that
$z_2$
such that
![]() $\|f-p\|_{\mathcal D(\mu _1, \mu _2)} < \epsilon .$
It is easy to see using Lemma 3.7 that there exists an
$\|f-p\|_{\mathcal D(\mu _1, \mu _2)} < \epsilon .$
It is easy to see using Lemma 3.7 that there exists an
![]() $R=(R_1, R_2) \in (0, 1)^2$
such that
$R=(R_1, R_2) \in (0, 1)^2$
such that
Since
![]() $f_R$
is holomorphic in an open neighborhood of
$f_R$
is holomorphic in an open neighborhood of
![]() ${\overline {\mathbb D}}^2,$
there exists a polynomial p such that
${\overline {\mathbb D}}^2,$
there exists a polynomial p such that
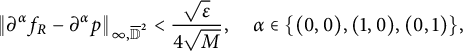 $$ \begin{align*}\|\partial^{\alpha}f_R-\partial^{\alpha}p\|_{\infty, {\overline{\mathbb D}^2}} < \frac{\sqrt{\epsilon}}{4\sqrt{M}}, \quad \alpha \in \{(0, 0), (1, 0), (0, 1)\},\end{align*} $$
$$ \begin{align*}\|\partial^{\alpha}f_R-\partial^{\alpha}p\|_{\infty, {\overline{\mathbb D}^2}} < \frac{\sqrt{\epsilon}}{4\sqrt{M}}, \quad \alpha \in \{(0, 0), (1, 0), (0, 1)\},\end{align*} $$
where
![]() $M=\max \big \{\int _{\mathbb D}P_{\mu _j}(w)dA(w) : j=1, 2\big \}+1.$
This together with the fact that the norm on
$M=\max \big \{\int _{\mathbb D}P_{\mu _j}(w)dA(w) : j=1, 2\big \}+1.$
This together with the fact that the norm on
![]() $H^2(\mathbb D^2)$
is dominated by the
$H^2(\mathbb D^2)$
is dominated by the
![]() $\|\cdot \|_{\infty , \overline {\mathbb D}^2}$
shows that
$\|\cdot \|_{\infty , \overline {\mathbb D}^2}$
shows that
![]() $\|f_{R}-p\|_{\mathcal D(\mu _1, \mu _2)} < \epsilon /2.$
Combining this with (3.10) yields
$\|f_{R}-p\|_{\mathcal D(\mu _1, \mu _2)} < \epsilon /2.$
Combining this with (3.10) yields
![]() $\|f-p\|_{\mathcal D(\mu _1, \mu _2)} < \epsilon ,$
which completes the proof.
$\|f-p\|_{\mathcal D(\mu _1, \mu _2)} < \epsilon ,$
which completes the proof.
The following provides a ground to discuss operator theory on
![]() $\mathcal D(\mu _1, \mu _2).$
$\mathcal D(\mu _1, \mu _2).$
Corollary 3.8 For
![]() $j=1, 2,$
let
$j=1, 2,$
let
![]() $\mathscr M_{z_j}$
denote the operator of multiplication by the coordinate function
$\mathscr M_{z_j}$
denote the operator of multiplication by the coordinate function
![]() $z_j.$
Then the commuting pair
$z_j.$
Then the commuting pair
![]() $\mathscr M_z=(\mathscr M_{z_1}, \mathscr M_{z_2})$
on
$\mathscr M_z=(\mathscr M_{z_1}, \mathscr M_{z_2})$
on
![]() $\mathcal D(\mu _1, \mu _2)$
is a cyclic toral
$\mathcal D(\mu _1, \mu _2)$
is a cyclic toral
![]() $2$
-isometry with cyclic vector
$2$
-isometry with cyclic vector
![]() $1.$
$1.$
Proof Note that by Theorem 2.1(i) and the closed graph theorem,
![]() $\mathscr M_z$
defines a pair of bounded linear operators
$\mathscr M_z$
defines a pair of bounded linear operators
![]() $\mathscr M_{z_1}$
and
$\mathscr M_{z_1}$
and
![]() $\mathscr M_{z_2}$
on
$\mathscr M_{z_2}$
on
![]() $\mathcal D(\mu _1, \mu _2).$
By Theorem 2.1(ii),
$\mathcal D(\mu _1, \mu _2).$
By Theorem 2.1(ii),
![]() $\mathscr M_z$
is cyclic with cyclic vector
$\mathscr M_z$
is cyclic with cyclic vector
![]() $1.$
Finally, the fact that
$1.$
Finally, the fact that
![]() $\mathscr M_z$
is a toral
$\mathscr M_z$
is a toral
![]() $2$
-isometry may be derived from (ii) and (iii) of Theorem 2.1.
$2$
-isometry may be derived from (ii) and (iii) of Theorem 2.1.
Let
![]() $\kappa : \mathbb D \times \mathbb D \rightarrow \mathbb C$
denote the reproducing kernel of
$\kappa : \mathbb D \times \mathbb D \rightarrow \mathbb C$
denote the reproducing kernel of
![]() $\mathcal D(\mu _1, \mu _2)$
(see Lemma 3.1).
$\mathcal D(\mu _1, \mu _2)$
(see Lemma 3.1).
Corollary 3.9 For any
![]() $w \in \mathbb D^2, \, \ker (\mathscr M_z- w)=\{0\}$
and
$w \in \mathbb D^2, \, \ker (\mathscr M_z- w)=\{0\}$
and
![]() $\ker (\mathscr M^*_z - w)$
is the one-dimensional space spanned by
$\ker (\mathscr M^*_z - w)$
is the one-dimensional space spanned by
![]() $\kappa (\cdot , \overline {w}).$
$\kappa (\cdot , \overline {w}).$
Proof Since
![]() $\mathcal D(\mu _1, \mu _2)$
is contained in the space of complex-valued holomorphic functions on
$\mathcal D(\mu _1, \mu _2)$
is contained in the space of complex-valued holomorphic functions on
![]() $\mathbb D^2,$
the pair
$\mathbb D^2,$
the pair
![]() $\mathscr M_z$
has no eigenvalue. By Theorem 2.1,
$\mathscr M_z$
has no eigenvalue. By Theorem 2.1,
![]() $\mathscr M_z$
is cyclic, and hence, for any
$\mathscr M_z$
is cyclic, and hence, for any
![]() $w \in \mathbb C^2,$
the dimension of
$w \in \mathbb C^2,$
the dimension of
![]() $\ker (\mathscr M^*_z - w)$
is at most
$\ker (\mathscr M^*_z - w)$
is at most
![]() $1$
(see (1.6)). If
$1$
(see (1.6)). If
![]() $w \in \mathbb D^2,$
then by the reproducing property of
$w \in \mathbb D^2,$
then by the reproducing property of
![]() $\mathcal D(\mu _1, \mu _2)$
(see Lemma 3.1),
$\mathcal D(\mu _1, \mu _2)$
(see Lemma 3.1),
![]() $\kappa (\cdot , \overline {w}) \in \ker (\mathscr M^*_z - w).$
Since
$\kappa (\cdot , \overline {w}) \in \ker (\mathscr M^*_z - w).$
Since
![]() $1 \in \mathcal D(\mu _1, \mu _2),$
once again by the reproducing property of
$1 \in \mathcal D(\mu _1, \mu _2),$
once again by the reproducing property of
![]() $\mathcal D(\mu _1, \mu _2), \kappa (\cdot , \overline {w})\neq 0.$
$\mathcal D(\mu _1, \mu _2), \kappa (\cdot , \overline {w})\neq 0.$
Before we state the next application of Theorem 2.1, we need a formula for the inner-product of monomials in
![]() $\mathcal D(\mu _1, \mu _2).$
$\mathcal D(\mu _1, \mu _2).$
Lemma 3.10 For
![]() $\mu \in M_+(\mathbb T)$
and
$\mu \in M_+(\mathbb T)$
and
![]() $j \geqslant 0,$
let
$j \geqslant 0,$
let
![]() $\hat {\mu }(j) = \int _{\mathbb T} \zeta ^{-j} d\mu (\zeta ).$
Then
$\hat {\mu }(j) = \int _{\mathbb T} \zeta ^{-j} d\mu (\zeta ).$
Then
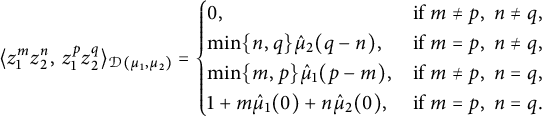 $$ \begin{align} \langle{z^{m}_1z^n_2},\,{z^{p}_1z^q_2} \rangle_{\mathcal D(\mu_1, \mu_2)} = \begin{cases} 0, & \text{if}~ m\neq p, ~n \neq q, \\ \min\{n, q\}\hat{\mu}_2(q-n), & \text{if}~ m=p, ~n \neq q, \\ \min\{m, p\}\hat{\mu}_1(p-m), & \text{if}~ m \neq p, ~n = q, \\ 1+m\hat{\mu}_1(0) + n\hat{\mu}_2(0), & \text{if}~ m= p, ~n = q. \end{cases} \end{align} $$
$$ \begin{align} \langle{z^{m}_1z^n_2},\,{z^{p}_1z^q_2} \rangle_{\mathcal D(\mu_1, \mu_2)} = \begin{cases} 0, & \text{if}~ m\neq p, ~n \neq q, \\ \min\{n, q\}\hat{\mu}_2(q-n), & \text{if}~ m=p, ~n \neq q, \\ \min\{m, p\}\hat{\mu}_1(p-m), & \text{if}~ m \neq p, ~n = q, \\ 1+m\hat{\mu}_1(0) + n\hat{\mu}_2(0), & \text{if}~ m= p, ~n = q. \end{cases} \end{align} $$
In particular, the monomials are orthogonal in
![]() $\mathcal D(\mu _1, \mu _2)$
if and only if
$\mathcal D(\mu _1, \mu _2)$
if and only if
![]() $\mu _1$
and
$\mu _1$
and
![]() $\mu _2$
are nonnegative multiples of the Lebesgue measure on
$\mu _2$
are nonnegative multiples of the Lebesgue measure on
![]() $\mathbb T.$
$\mathbb T.$
Proof Fix nonnegative integers
![]() $m, n, p, q.$
By the polarization identity,
$m, n, p, q.$
By the polarization identity,
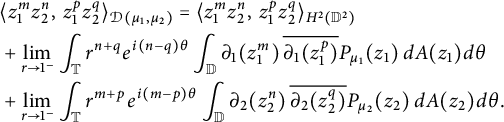 $$ \begin{align*} & \langle{z^{m}_1z^n_2},\,{z^{p}_1z^q_2} \rangle_{\mathcal D(\mu_1, \mu_2)} = \langle{z^{m}_1z^n_2},\,{z^{p}_1z^q_2} \rangle_{H^2(\mathbb D^2)} \\ &+ \lim_{r \rightarrow 1^{-}} \int_{\mathbb T} r^{n+q} e^{i (n-q) \theta} \int_{\mathbb D} \partial_1(z^m_1) \, \overline{\partial_1(z^p_1)} P_{\mu_1}(z_1) \,dA(z_1)d\theta \\ &+ \lim_{r \rightarrow 1^{-}} \int_{\mathbb T} r^{m+p}e^{i (m-p) \theta} \int_{\mathbb D} \partial_2(z^n_2) \, \overline{\partial_2(z^q_2) } P_{\mu_2}(z_2) \,dA(z_2)d\theta. \end{align*} $$
$$ \begin{align*} & \langle{z^{m}_1z^n_2},\,{z^{p}_1z^q_2} \rangle_{\mathcal D(\mu_1, \mu_2)} = \langle{z^{m}_1z^n_2},\,{z^{p}_1z^q_2} \rangle_{H^2(\mathbb D^2)} \\ &+ \lim_{r \rightarrow 1^{-}} \int_{\mathbb T} r^{n+q} e^{i (n-q) \theta} \int_{\mathbb D} \partial_1(z^m_1) \, \overline{\partial_1(z^p_1)} P_{\mu_1}(z_1) \,dA(z_1)d\theta \\ &+ \lim_{r \rightarrow 1^{-}} \int_{\mathbb T} r^{m+p}e^{i (m-p) \theta} \int_{\mathbb D} \partial_2(z^n_2) \, \overline{\partial_2(z^q_2) } P_{\mu_2}(z_2) \,dA(z_2)d\theta. \end{align*} $$
Since
![]() $\langle {z^{m}_1z^n_2},\,{z^{p}_1z^q_2} \rangle _{H^2(\mathbb D^2)}=\delta (m, p)\delta (n, q)$
with
$\langle {z^{m}_1z^n_2},\,{z^{p}_1z^q_2} \rangle _{H^2(\mathbb D^2)}=\delta (m, p)\delta (n, q)$
with
![]() $\delta (\cdot , \cdot )$
denoting the Kronecker delta of two variables, (3.11) may be deduced from the following formula for the inner-product of the Dirichlet-type space
$\delta (\cdot , \cdot )$
denoting the Kronecker delta of two variables, (3.11) may be deduced from the following formula for the inner-product of the Dirichlet-type space
![]() $\mathcal D(\mu )$
(see [Reference Olofsson22, Equation (3.2)]):
$\mathcal D(\mu )$
(see [Reference Olofsson22, Equation (3.2)]):
(this formula may also be derived directly using [Reference Rudin28, Theorem 11.9]). The “In particular” part follows from the Weierstrass approximation theorem and Riesz representation theorem.
Remark 3.11 Assume that
![]() $\mu _1, \mu _2$
are nonzero. It is easy to see using (3.11) and (3.12) that
$\mu _1, \mu _2$
are nonzero. It is easy to see using (3.11) and (3.12) that
![]() $\|f\|_{\mathcal D(\mu _1, \mu _2)} = \|f\|_{\mathcal D(\mu _1) \otimes \mathcal D(\mu _2)}$
holds for all monomials f if and only if at least one of
$\|f\|_{\mathcal D(\mu _1, \mu _2)} = \|f\|_{\mathcal D(\mu _1) \otimes \mathcal D(\mu _2)}$
holds for all monomials f if and only if at least one of
![]() $\mu _1$
and
$\mu _1$
and
![]() $\mu _2$
is the zero measure. In particular,
$\mu _2$
is the zero measure. In particular,
![]() $\mathcal D(\mu _1, \mu _2) \neq \mathcal D(\mu _1) \otimes \mathcal D(\mu _2),$
in general.
$\mathcal D(\mu _1, \mu _2) \neq \mathcal D(\mu _1) \otimes \mathcal D(\mu _2),$
in general.
The following is a consequence of (3.11) (see Definition 1.5).
Corollary 3.12 For
![]() $\mu _1, \mu _2 \in M_+(\mathbb T),$
the subspace of
$\mu _1, \mu _2 \in M_+(\mathbb T),$
the subspace of
![]() $\mathcal D(\mu _1, \mu _2)$
spanned by the constant function
$\mathcal D(\mu _1, \mu _2)$
spanned by the constant function
![]() $1$
is a wandering subspace for
$1$
is a wandering subspace for
![]() $\mathscr M_z$
on
$\mathscr M_z$
on
![]() $\mathcal D(\mu _1, \mu _2).$
$\mathcal D(\mu _1, \mu _2).$
A bounded linear operator T on a Hilbert space is essentially normal if
![]() $T^*T-TT^*$
is a compact operator. An essentially normal operator is said to be essentially unitary if
$T^*T-TT^*$
is a compact operator. An essentially normal operator is said to be essentially unitary if
![]() $T^*T-I$
is compact. Unlike the case of one variable Dirichlet-type spaces (see [Reference Chavan7, Proposition 2.21]),
$T^*T-I$
is compact. Unlike the case of one variable Dirichlet-type spaces (see [Reference Chavan7, Proposition 2.21]),
![]() $\mathcal D(\mu _1, \mu _2)$
does not support essentially normal multiplication
$\mathcal D(\mu _1, \mu _2)$
does not support essentially normal multiplication
![]() $2$
-tuple
$2$
-tuple
![]() $\mathscr M_z.$
$\mathscr M_z.$
Corollary 3.13 The multiplication operators
![]() $\mathscr M_{z_1}$
and
$\mathscr M_{z_1}$
and
![]() $\mathscr M_{z_2}$
on
$\mathscr M_{z_2}$
on
![]() $\mathcal D(\mu _1, \mu _2)$
are never essentially normal.
$\mathcal D(\mu _1, \mu _2)$
are never essentially normal.
Proof By Corollary 3.8, the multiplication
![]() $2$
-tuple
$2$
-tuple
![]() $\mathscr M_z$
is a toral
$\mathscr M_z$
is a toral
![]() $2$
-isometry. In particular,
$2$
-isometry. In particular,
![]() $\mathscr M_{z_1}$
and
$\mathscr M_{z_1}$
and
![]() $\mathscr M_{z_2}$
are
$\mathscr M_{z_2}$
are
![]() $2$
-isometries. If these are essentially normal, then the image of
$2$
-isometries. If these are essentially normal, then the image of
![]() $\mathscr M_{z_1}$
and
$\mathscr M_{z_1}$
and
![]() $\mathscr M_{z_2}$
in the Calkin algebra is a normal
$\mathscr M_{z_2}$
in the Calkin algebra is a normal
![]() $2$
-isometry, and hence
$2$
-isometry, and hence
![]() $\mathscr M_{z_1}$
and
$\mathscr M_{z_1}$
and
![]() $\mathscr M_{z_2}$
are essentially unitary (since a normal
$\mathscr M_{z_2}$
are essentially unitary (since a normal
![]() $2$
-isometry, being invertible, is a unitary). It follows that
$2$
-isometry, being invertible, is a unitary). It follows that
![]() $\mathscr M_{z_1}$
and
$\mathscr M_{z_1}$
and
![]() $\mathscr M_{z_2}$
are Fredholm. In view of Atkinson’s theorem (see [Reference Conway9, Theorem XI.2.3]), it suffices to check that the kernels of
$\mathscr M_{z_2}$
are Fredholm. In view of Atkinson’s theorem (see [Reference Conway9, Theorem XI.2.3]), it suffices to check that the kernels of
![]() $\mathscr M^*_{z_1}$
and
$\mathscr M^*_{z_1}$
and
![]() $\mathscr M^*_{z_2}$
are of infinite dimension. To see this, fix a nonnegative integer
$\mathscr M^*_{z_2}$
are of infinite dimension. To see this, fix a nonnegative integer
![]() $j.$
Note that by (3.11),
$j.$
Note that by (3.11),
and hence by the linearity of the inner-product and the density of the polynomials in
![]() $\mathcal D(\mu _1, \mu _2)$
(see Theorem 2.1(ii)), we obtain
$\mathcal D(\mu _1, \mu _2)$
(see Theorem 2.1(ii)), we obtain
![]() $\mathscr M^*_{z_1}z^j_2=0.$
Similarly, one can check that
$\mathscr M^*_{z_1}z^j_2=0.$
Similarly, one can check that
![]() $z^j_1 \in \ker \mathscr M^*_{z_2},$
completing the proof.
$z^j_1 \in \ker \mathscr M^*_{z_2},$
completing the proof.
4 Proof of Theorem 2.2 and a consequence
We begin the proof of Theorem 2.2 with the following special case.
Lemma 4.1 The Hardy space
![]() $H^2(\mathbb D^2)$
has the division property.
$H^2(\mathbb D^2)$
has the division property.
Proof For
![]() $j=1, 2$
and
$j=1, 2$
and
![]() $\lambda =(\lambda _1, \lambda _2) \in \mathbb D^2,$
let
$\lambda =(\lambda _1, \lambda _2) \in \mathbb D^2,$
let
![]() $f \in H^2(\mathbb D^2)$
be such that
$f \in H^2(\mathbb D^2)$
be such that
![]() $\{z \in \mathbb D^2 : z_j =\lambda _j\} \subseteq Z(f).$
Let
$\{z \in \mathbb D^2 : z_j =\lambda _j\} \subseteq Z(f).$
Let
![]() $w=(w_1, w_2) \in \mathbb D^2.$
If
$w=(w_1, w_2) \in \mathbb D^2.$
If
![]() $w_j \neq \lambda _j,$
then clearly
$w_j \neq \lambda _j,$
then clearly
![]() $g_j(z) =\frac {f(z)}{z_j-\lambda _j}$
defines a holomorphic function in a neighborhood of
$g_j(z) =\frac {f(z)}{z_j-\lambda _j}$
defines a holomorphic function in a neighborhood of
![]() $w.$
If
$w.$
If
![]() $w_j =\lambda _j,$
then since
$w_j =\lambda _j,$
then since
![]() $\{z \in \mathbb D^2 : z_j =\lambda _j\} \subseteq Z(f), f$
as a function of
$\{z \in \mathbb D^2 : z_j =\lambda _j\} \subseteq Z(f), f$
as a function of
![]() $z_j$
has a removable singularity at
$z_j$
has a removable singularity at
![]() $w_j,$
and hence by Hartogs’ separate analyticity theorem (see [Reference Rudin27, pp. 1–Reference Agler and Stankus2]),
$w_j,$
and hence by Hartogs’ separate analyticity theorem (see [Reference Rudin27, pp. 1–Reference Agler and Stankus2]),
![]() $g_j$
as above extends holomorphically in a neighborhood of
$g_j$
as above extends holomorphically in a neighborhood of
![]() $w.$
This shows that
$w.$
This shows that
![]() $g_j$
is holomorphic on
$g_j$
is holomorphic on
![]() $\mathbb D^2.$
To see that
$\mathbb D^2.$
To see that
![]() $g_j \in H^2(\mathbb D^2),$
note that for
$g_j \in H^2(\mathbb D^2),$
note that for
![]() $r \in (|\lambda _j|, 1)$
and
$r \in (|\lambda _j|, 1)$
and
![]() $\theta _1, \theta _2 \in [0, 2\pi ],$
$\theta _1, \theta _2 \in [0, 2\pi ],$
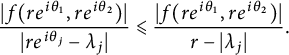 $$ \begin{align*} \frac{|f(re^{i \theta_1}, re^{i \theta_2})|}{|re^{i \theta_j}-\lambda_j|} \leqslant \frac{|f(re^{i \theta_1}, re^{i \theta_2})|}{r-|\lambda_j|}. \end{align*} $$
$$ \begin{align*} \frac{|f(re^{i \theta_1}, re^{i \theta_2})|}{|re^{i \theta_j}-\lambda_j|} \leqslant \frac{|f(re^{i \theta_1}, re^{i \theta_2})|}{r-|\lambda_j|}. \end{align*} $$
Since
![]() $f \in H^2(\mathbb D^2),$
it may now be deduced from (1.4) that
$f \in H^2(\mathbb D^2),$
it may now be deduced from (1.4) that
![]() $g_j \in H^2(\mathbb D^2).$
$g_j \in H^2(\mathbb D^2).$
Remark 4.2 One may argue as above to see that for any positive integer
![]() $d,$
the Hardy space
$d,$
the Hardy space
![]() $H^2(\mathbb D^d)$
has the division property.
$H^2(\mathbb D^d)$
has the division property.
We also need the following fact essentially noticed in [Reference Richter26].
Lemma 4.3 For any
![]() $\mu \in M_+(\mathbb T), \mathcal D(\mu )$
has the division property.
$\mu \in M_+(\mathbb T), \mathcal D(\mu )$
has the division property.
Proof For
![]() $\lambda \in \mathbb D,$
let
$\lambda \in \mathbb D,$
let
![]() $g \in \mathcal D(\mu )$
be such that
$g \in \mathcal D(\mu )$
be such that
![]() $g(\lambda )=0.$
Note that g is orthogonal to
$g(\lambda )=0.$
Note that g is orthogonal to
![]() $\kappa (\cdot , \lambda ).$
Since
$\kappa (\cdot , \lambda ).$
Since
![]() $\ker (\mathscr M^*_z-\overline {\lambda })$
is spanned by
$\ker (\mathscr M^*_z-\overline {\lambda })$
is spanned by
![]() $\kappa (\cdot , \lambda )$
and the range of
$\kappa (\cdot , \lambda )$
and the range of
![]() $\mathscr M_z-\lambda $
is closed (see [Reference Richter26, Corollary 3.8]), there exists
$\mathscr M_z-\lambda $
is closed (see [Reference Richter26, Corollary 3.8]), there exists
![]() $f \in \mathcal D(\mu )$
such that
$f \in \mathcal D(\mu )$
such that
![]() $g=(z-\lambda )f,$
which completes the proof.
$g=(z-\lambda )f,$
which completes the proof.
Proof (Proof of Theorem 2.2)
For
![]() $\lambda \in \mathbb D,$
assume that
$\lambda \in \mathbb D,$
assume that
![]() $(z_j-\lambda )h \in \mathcal D(\mu _1, \mu _2)$
for some
$(z_j-\lambda )h \in \mathcal D(\mu _1, \mu _2)$
for some
![]() $j=1, 2.$
Thus
$j=1, 2.$
Thus
Since the arguments for the cases
![]() $j=1, 2$
are similar, we only treat the case when
$j=1, 2$
are similar, we only treat the case when
![]() $j=1.$
It follows from Lemma 4.1 and (4.1) that
$j=1.$
It follows from Lemma 4.1 and (4.1) that
![]() $h \in H^2(\mathbb D^2).$
Applying (3.4) to (4.2) gives
$h \in H^2(\mathbb D^2).$
Applying (3.4) to (4.2) gives
where
![]() $\Omega _r$
is a Lebesgue measurable subset of
$\Omega _r$
is a Lebesgue measurable subset of
![]() $[0, 2\pi ]$
such that
$[0, 2\pi ]$
such that
![]() $[0, 2\pi ] \backslash \Omega _r$
is of measure
$[0, 2\pi ] \backslash \Omega _r$
is of measure
![]() $0.$
For
$0.$
For
![]() $r \in (0, 1)$
and
$r \in (0, 1)$
and
![]() $\theta \in \Omega _r,$
consider
$\theta \in \Omega _r,$
consider
![]() $f_{r, \theta } : \mathbb D \rightarrow \mathbb C$
defined by
$f_{r, \theta } : \mathbb D \rightarrow \mathbb C$
defined by
By (4.1) and Lemma 3.2,
![]() $f_{r, \theta }$
belongs to
$f_{r, \theta }$
belongs to
![]() $H^2(\mathbb D).$
Hence, by (4.3),
$H^2(\mathbb D).$
Hence, by (4.3),
![]() $f_{r, \theta }$
belongs to
$f_{r, \theta }$
belongs to
![]() $\mathcal D(\mu _1).$
Hence, by Lemma 4.3,
$\mathcal D(\mu _1).$
Hence, by Lemma 4.3,
![]() $h(\cdot , re^{i \theta }) \in \mathcal D(\mu _1).$
Since
$h(\cdot , re^{i \theta }) \in \mathcal D(\mu _1).$
Since
(see [Reference Richter26, Theorem 3.6]), by the reverse triangle inequality,
Integrating both sides over
![]() $[0, 2\pi ]$
yields
$[0, 2\pi ]$
yields
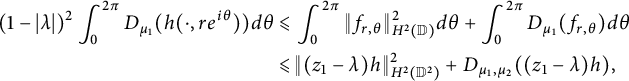 $$ \begin{align*} (1-|\lambda|)^2\int_{0}^{2\pi} D_{\mu_1}(h(\cdot, re^{i \theta}))d\theta \leqslant &\, \int_{0}^{2\pi}\|f_{r, \theta}\|^2_{H^2(\mathbb D)}d\theta + \int_{0}^{2\pi}D_{\mu_1}(f_{r, \theta})d\theta \\ \leqslant &\, \|(z_1-\lambda)h\|^2_{H^2(\mathbb D^2)} + D_{\mu_1, \mu_2}((z_1 -\lambda)h), \end{align*} $$
$$ \begin{align*} (1-|\lambda|)^2\int_{0}^{2\pi} D_{\mu_1}(h(\cdot, re^{i \theta}))d\theta \leqslant &\, \int_{0}^{2\pi}\|f_{r, \theta}\|^2_{H^2(\mathbb D)}d\theta + \int_{0}^{2\pi}D_{\mu_1}(f_{r, \theta})d\theta \\ \leqslant &\, \|(z_1-\lambda)h\|^2_{H^2(\mathbb D^2)} + D_{\mu_1, \mu_2}((z_1 -\lambda)h), \end{align*} $$
where we used (3.2). Taking supremum over
![]() $r \in (0, 1)$
gives now
$r \in (0, 1)$
gives now
Also, since
![]() $h \in H^2(\mathbb D^2),$
it now suffices to check that
$h \in H^2(\mathbb D^2),$
it now suffices to check that
Note that by (4.2),
However, for any
![]() $s \in (|\lambda |, 1),$
$s \in (|\lambda |, 1),$
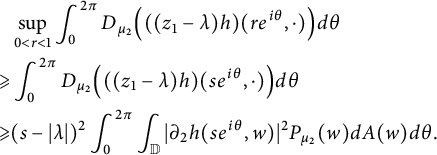 $$ \begin{align*} & \sup_{0 < r < 1} \int_{0}^{2\pi} D_{\mu_2}\Big(((z_1-\lambda)h)(re^{i \theta}, \cdot)\Big)d\theta \\ \geqslant & \int_{0}^{2\pi} D_{\mu_2}\Big(((z_1-\lambda)h)(se^{i \theta}, \cdot)\Big)d\theta \\ \geqslant & (s-|\lambda|)^2 \int_{0}^{2\pi} \int_{\mathbb D} |\partial_2 h(se^{i \theta}, w)|^2 P_{\mu_2}(w)dA(w)d\theta. \end{align*} $$
$$ \begin{align*} & \sup_{0 < r < 1} \int_{0}^{2\pi} D_{\mu_2}\Big(((z_1-\lambda)h)(re^{i \theta}, \cdot)\Big)d\theta \\ \geqslant & \int_{0}^{2\pi} D_{\mu_2}\Big(((z_1-\lambda)h)(se^{i \theta}, \cdot)\Big)d\theta \\ \geqslant & (s-|\lambda|)^2 \int_{0}^{2\pi} \int_{\mathbb D} |\partial_2 h(se^{i \theta}, w)|^2 P_{\mu_2}(w)dA(w)d\theta. \end{align*} $$
Applying Lemma 1.1 and letting
![]() $s \uparrow 1^{-}$
now yields (4.4).
$s \uparrow 1^{-}$
now yields (4.4).
Before we present an application of Theorem 2.2, let us recall some facts from the multivariate spectral theory (see [Reference Curto11, Reference Curto, Conway and Morrel12, Reference Taylor30]). Let
![]() $T=(T_1, T_2)$
be a commuting pair on
$T=(T_1, T_2)$
be a commuting pair on
![]() $\mathcal H$
and set
$\mathcal H$
and set
![]() $D_T(x)=(T_1x, T_2x), x \in \mathcal H.$
Note that
$D_T(x)=(T_1x, T_2x), x \in \mathcal H.$
Note that
Indeed, if
![]() $D^*_TD_T$
is Fredholm, then
$D^*_TD_T$
is Fredholm, then
![]() $D_T$
is left-Fredholm, and hence we obtain (4.5). To define the Taylor spectrum, we consider the following complex:
$D_T$
is left-Fredholm, and hence we obtain (4.5). To define the Taylor spectrum, we consider the following complex:
where the boundary maps
![]() $B_1$
and
$B_1$
and
![]() $B_2$
are given by
$B_2$
are given by
Note that
![]() $K(T, \mathcal H)$
is a complex, that is,
$K(T, \mathcal H)$
is a complex, that is,
![]() $ B_1 \circ B_2 = 0.$
Let
$ B_1 \circ B_2 = 0.$
Let
![]() $H^k({T})$
denote the kth cohomology group in
$H^k({T})$
denote the kth cohomology group in
![]() $K({T},\mathcal {H}), k=0, 1, 2.$
Following [Reference Taylor30] (resp. [Reference Curto11]), we say that T is Taylor-invertible (resp. Fredholm) if
$K({T},\mathcal {H}), k=0, 1, 2.$
Following [Reference Taylor30] (resp. [Reference Curto11]), we say that T is Taylor-invertible (resp. Fredholm) if
![]() $H^k({T})=\{0\}$
(resp.
$H^k({T})=\{0\}$
(resp.
![]() $\dim H^k({T})<\infty $
) for
$\dim H^k({T})<\infty $
) for
![]() $k=0, 1, 2.$
The Taylor spectrum
$k=0, 1, 2.$
The Taylor spectrum
![]() $\sigma (T)$
and the essential spectrum
$\sigma (T)$
and the essential spectrum
![]() $\sigma _e(T)$
are given by
$\sigma _e(T)$
are given by
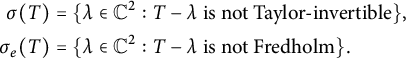 $$ \begin{align*} \sigma(T)&=\{\lambda \in \mathbb C^2 : T-\lambda~\text{is not Taylor-invertible}\}, \\ \sigma_e(T)&=\{\lambda \in \mathbb C^2 : T-\lambda~\text{is not Fredholm}\}. \end{align*} $$
$$ \begin{align*} \sigma(T)&=\{\lambda \in \mathbb C^2 : T-\lambda~\text{is not Taylor-invertible}\}, \\ \sigma_e(T)&=\{\lambda \in \mathbb C^2 : T-\lambda~\text{is not Fredholm}\}. \end{align*} $$
The Fredholm index
![]() $\text {ind}({T})$
of a Fredholm commuting
$\text {ind}({T})$
of a Fredholm commuting
![]() $2$
-tuple
$2$
-tuple
![]() ${T}$
on
${T}$
on
![]() $\mathcal H$
is the Euler characteristic of the Koszul complex
$\mathcal H$
is the Euler characteristic of the Koszul complex
![]() $K({T}, \mathcal {H}),$
that is,
$K({T}, \mathcal {H}),$
that is,
As an application of the division property, we now show that we always have exactness at the middle stage of the Koszul complex of the multiplication
![]() $2$
-tuple
$2$
-tuple
![]() $\mathscr M_z$
on
$\mathscr M_z$
on
![]() $\mathcal D(\mu _1, \mu _2).$
First, a general fact.
$\mathcal D(\mu _1, \mu _2).$
First, a general fact.
Lemma 4.4 Let
![]() $\mathscr H$
be a reproducing kernel Hilbert space of complex-valued holomorphic functions on the unit bidisc
$\mathscr H$
be a reproducing kernel Hilbert space of complex-valued holomorphic functions on the unit bidisc
![]() $\mathbb D^2.$
Assume that
$\mathbb D^2.$
Assume that
![]() $\mathscr M_z=(\mathscr M_{z_1}, \mathscr M_{z_2})$
is a commuting pair on
$\mathscr M_z=(\mathscr M_{z_1}, \mathscr M_{z_2})$
is a commuting pair on
![]() $\mathscr H.$
If
$\mathscr H.$
If
![]() $\mathscr H$
has the division property, then for every
$\mathscr H$
has the division property, then for every
![]() $\lambda = (\lambda _1, \lambda _2) \in \mathbb D^2,$
the Koszul complex of
$\lambda = (\lambda _1, \lambda _2) \in \mathbb D^2,$
the Koszul complex of
![]() $\mathscr M_z-\lambda = (\mathscr M_{z_1}-\lambda _1, \mathscr M_{z_2}-\lambda _2)$
is exact at the middle stage
$\mathscr M_z-\lambda = (\mathscr M_{z_1}-\lambda _1, \mathscr M_{z_2}-\lambda _2)$
is exact at the middle stage
![]() $($
see (4.6)
$($
see (4.6)
![]() $).$
$).$
Proof Note that
![]() $\mathscr H$
has the division property if and only if for
$\mathscr H$
has the division property if and only if for
![]() $j=1, 2,$
we have the following property:
$j=1, 2,$
we have the following property:
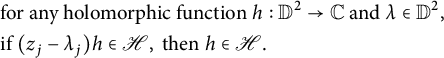 $$ \begin{align} &\text{for any holomorphic function } h : \mathbb D^2 \rightarrow \mathbb C \text{ and } \lambda \in \mathbb D^2, \notag \\&\text{if } (z_j-\lambda_j)h \in \mathscr H, \text{ then } h \in \mathscr H. \end{align} $$
$$ \begin{align} &\text{for any holomorphic function } h : \mathbb D^2 \rightarrow \mathbb C \text{ and } \lambda \in \mathbb D^2, \notag \\&\text{if } (z_j-\lambda_j)h \in \mathscr H, \text{ then } h \in \mathscr H. \end{align} $$
We first assume that (4.8) holds for
![]() $j=2$
. To see that the Koszul complex of
$j=2$
. To see that the Koszul complex of
![]() $\mathscr M_z-\lambda $
is exact at the middle stage, let
$\mathscr M_z-\lambda $
is exact at the middle stage, let
![]() $g, h \in \mathscr H$
be such that
$g, h \in \mathscr H$
be such that
Letting
![]() $z_2=\lambda _2,$
we obtain
$z_2=\lambda _2,$
we obtain
![]() $(w-\lambda _1)h(w, \lambda _2)=0$
for every
$(w-\lambda _1)h(w, \lambda _2)=0$
for every
![]() $w \in \mathbb D.$
It follows that
$w \in \mathbb D.$
It follows that
![]() $h(\cdot , \lambda _2)=0$
on
$h(\cdot , \lambda _2)=0$
on
![]() $\mathbb D.$
Since
$\mathbb D.$
Since
![]() $h : \mathbb D^2 \rightarrow \mathbb C$
is holomorphic, there exists a holomorphic function
$h : \mathbb D^2 \rightarrow \mathbb C$
is holomorphic, there exists a holomorphic function
![]() $k : \mathbb D^2 \rightarrow \mathbb C$
such that
$k : \mathbb D^2 \rightarrow \mathbb C$
such that
(in case of
![]() $\lambda _2=0,$
this can be seen using the power series for h; the general case can be dealt now by replacing
$\lambda _2=0,$
this can be seen using the power series for h; the general case can be dealt now by replacing
![]() $h(z_1, z_2)$
by
$h(z_1, z_2)$
by
![]() $h(z_1, \varphi (z_2)),$
where
$h(z_1, \varphi (z_2)),$
where
![]() $\varphi $
is the automorphism of
$\varphi $
is the automorphism of
![]() $\mathbb D$
which takes
$\mathbb D$
which takes
![]() $\lambda _2$
to
$\lambda _2$
to
![]() $0$
). Since
$0$
). Since
![]() $h \in \mathscr H,$
by (4.8),
$h \in \mathscr H,$
by (4.8),
![]() $k \in \mathscr H.$
We now combine (4.9) with (4.10) to obtain
$k \in \mathscr H.$
We now combine (4.9) with (4.10) to obtain
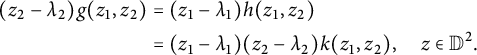 $$ \begin{align*} (z_2-\lambda_2)g(z_1, z_2)&=(z_1 - \lambda_1)h(z_1, z_2) \\ &= (z_1 - \lambda_1)(z_2 -\lambda_2)k(z_1, z_2), \quad z \in \mathbb D^2. \end{align*} $$
$$ \begin{align*} (z_2-\lambda_2)g(z_1, z_2)&=(z_1 - \lambda_1)h(z_1, z_2) \\ &= (z_1 - \lambda_1)(z_2 -\lambda_2)k(z_1, z_2), \quad z \in \mathbb D^2. \end{align*} $$
This gives
![]() $g(z_1, z_2)=(z_1-\lambda _1) k(z_1, z_2), z \in \mathbb D^2.$
This together with (4.10) shows that
$g(z_1, z_2)=(z_1-\lambda _1) k(z_1, z_2), z \in \mathbb D^2.$
This together with (4.10) shows that
![]() $\mathscr M_z-\lambda $
is exact at the middle stage. We may also obtain the same conclusion in case (4.8) holds for
$\mathscr M_z-\lambda $
is exact at the middle stage. We may also obtain the same conclusion in case (4.8) holds for
![]() $j=1$
. Indeed, one may proceed as above with the only change that the roles of
$j=1$
. Indeed, one may proceed as above with the only change that the roles of
![]() $\lambda _1$
and
$\lambda _1$
and
![]() $\lambda _2$
are interchanged (e.g. (4.9) is evaluated at
$\lambda _2$
are interchanged (e.g. (4.9) is evaluated at
![]() $z_1=\lambda _1$
).
$z_1=\lambda _1$
).
Remark 4.5 Let
![]() $\Omega $
be a bounded domain in
$\Omega $
be a bounded domain in
![]() $\mathbb C^2$
. One may imitate the first part of the proof of Lemma 4.1 to show that there exists a holomorphic function
$\mathbb C^2$
. One may imitate the first part of the proof of Lemma 4.1 to show that there exists a holomorphic function
![]() $k : \Omega \rightarrow \mathbb C$
satisfying (4.10). This gives an analog of Lemma 4.4 for arbitrary bounded domains.
$k : \Omega \rightarrow \mathbb C$
satisfying (4.10). This gives an analog of Lemma 4.4 for arbitrary bounded domains.
The following is a consequence of Theorem 2.2 and Lemma 4.4.
Corollary 4.6 For every
![]() $\lambda = (\lambda _1, \lambda _2) \in \mathbb D^2,$
the Koszul complex of the
$\lambda = (\lambda _1, \lambda _2) \in \mathbb D^2,$
the Koszul complex of the
![]() $2$
-tuple
$2$
-tuple
![]() $\mathscr M_z-\lambda = (\mathscr M_{z_1}-\lambda _1, \mathscr M_{z_2}-\lambda _2)$
on
$\mathscr M_z-\lambda = (\mathscr M_{z_1}-\lambda _1, \mathscr M_{z_2}-\lambda _2)$
on
![]() $\mathcal D(\mu _1, \mu _2)$
is exact at the middle stage
$\mathcal D(\mu _1, \mu _2)$
is exact at the middle stage
![]() $($
see (4.6)
$($
see (4.6)
![]() $).$
$).$
5 Proof of Theorem 2.3 and its consequences
We begin with a lemma, which is a variant of [Reference Ghara, Misra, Curto, Helton, Lin, Tang, Yang and Yu17, Lemma 4.14]. We include its proof for the sake of completeness.
Lemma 5.1 For a domain
![]() $\Omega $
of
$\Omega $
of
![]() $\mathbb C^2,$
let
$\mathbb C^2,$
let
![]() $\mathscr H$
be the reproducing kernel Hilbert space of complex-valued holomorphic functions associated with the kernel
$\mathscr H$
be the reproducing kernel Hilbert space of complex-valued holomorphic functions associated with the kernel
![]() $\kappa : \Omega \times \Omega \rightarrow \mathbb C.$
Assume that the constant function
$\kappa : \Omega \times \Omega \rightarrow \mathbb C.$
Assume that the constant function
![]() $1$
belongs to
$1$
belongs to
![]() $\mathscr H,$
the multiplication operators
$\mathscr H,$
the multiplication operators
![]() $\mathscr M_{z_1}, \mathscr M_{z_2}$
are bounded on
$\mathscr M_{z_1}, \mathscr M_{z_2}$
are bounded on
![]() $\mathscr H$
and the commuting
$\mathscr H$
and the commuting
![]() $2$
-tuple
$2$
-tuple
![]() $\mathscr M_z$
is cyclic. For
$\mathscr M_z$
is cyclic. For
![]() $w \in \Omega ,$
Gleason’s problem can be solved for
$w \in \Omega ,$
Gleason’s problem can be solved for
![]() $\mathscr H$
over
$\mathscr H$
over
![]() $\{w\}$
if and only if
$\{w\}$
if and only if
In particular, Gleason’s problem can be solved for
![]() $\mathscr H$
over
$\mathscr H$
over
![]() $\Omega \backslash \sigma _e(\mathscr M_z).$
$\Omega \backslash \sigma _e(\mathscr M_z).$
Proof Let
![]() $w \in \Omega $
, and let
$w \in \Omega $
, and let
![]() $f \in \mathscr H.$
By the reproducing kernel property of
$f \in \mathscr H.$
By the reproducing kernel property of
![]() $\mathscr H,$
$\mathscr H,$
However, since
![]() $\mathscr M_z$
is cyclic,
$\mathscr M_z$
is cyclic,
![]() $\dim \ker (\mathscr M^*_z-\overline {w}) \leqslant 1$
for every
$\dim \ker (\mathscr M^*_z-\overline {w}) \leqslant 1$
for every
![]() $w \in \mathbb C^2$
(see (1.6)). As
$w \in \mathbb C^2$
(see (1.6)). As
![]() $1 \in \mathscr H,$
we have
$1 \in \mathscr H,$
we have
![]() $\kappa (\cdot , w) \neq 0,$
and hence
$\kappa (\cdot , w) \neq 0,$
and hence
It now follows from (5.2) that
Also, it is easy to see that
If (5.1) holds, then it now follows from (5.3) that
and hence Gleason’s problem can be solved for
![]() $\mathscr H$
over
$\mathscr H$
over
![]() $\{w\}.$
Conversely, if Gleason’s problem can be solved for
$\{w\}.$
Conversely, if Gleason’s problem can be solved for
![]() $\mathscr H$
over
$\mathscr H$
over
![]() $\{w\},$
then by (5.3), any function in
$\{w\},$
then by (5.3), any function in
![]() $\overline {\text {ran}(D^*_{\mathscr M^*_z-\overline {w}})}$
is of the form
$\overline {\text {ran}(D^*_{\mathscr M^*_z-\overline {w}})}$
is of the form
![]() $f-f(w)$
for some
$f-f(w)$
for some
![]() $f \in \mathscr H,$
and hence by (5.4), it belongs to
$f \in \mathscr H,$
and hence by (5.4), it belongs to
![]() $\text {ran}(D^*_{\mathscr M^*_z-\overline {w}}).$
This completes the proof of the equivalence.
$\text {ran}(D^*_{\mathscr M^*_z-\overline {w}}).$
This completes the proof of the equivalence.
To see the remaining part, let
![]() $w = (w_1, w_2) \in \Omega \backslash \sigma _e(\mathscr M_z).$
Since
$w = (w_1, w_2) \in \Omega \backslash \sigma _e(\mathscr M_z).$
Since
![]() $D^*_SD_S = S^*_1S_1 + S^*_2S_2$
for any commuting pair
$D^*_SD_S = S^*_1S_1 + S^*_2S_2$
for any commuting pair
![]() $S=(S_1, S_2),$
by [Reference Curto11, Corollary 3.6], the operator
$S=(S_1, S_2),$
by [Reference Curto11, Corollary 3.6], the operator
![]() $D^*_{\mathscr M^*_z-\overline {w}}D_{\mathscr M^*_z-\overline {w}}$
is Fredholm, and hence by (4.5),
$D^*_{\mathscr M^*_z-\overline {w}}D_{\mathscr M^*_z-\overline {w}}$
is Fredholm, and hence by (4.5),
![]() $D_{\mathscr M^*_z-\overline {w}}$
has closed range. Hence, by the closed-range theorem (see [Reference Conway9, Theorem VI.1.10]), we obtain (5.1) completing the proof.
$D_{\mathscr M^*_z-\overline {w}}$
has closed range. Hence, by the closed-range theorem (see [Reference Conway9, Theorem VI.1.10]), we obtain (5.1) completing the proof.
Remark 5.2 Let
![]() $\mathscr M_z$
be the multiplication
$\mathscr M_z$
be the multiplication
![]() $2$
-tuple on the Hardy space
$2$
-tuple on the Hardy space
![]() $H^2(\mathbb D^2)$
of the unit bidisc
$H^2(\mathbb D^2)$
of the unit bidisc
![]() $\mathbb D^2.$
Since
$\mathbb D^2.$
Since
![]() $\sigma _e(\mathscr M_z) \cap \mathbb D^2 = \emptyset $
(see [Reference Curto11, Theorem 5(c)]), by Lemma 5.1, Gleason’s problem can be solved for
$\sigma _e(\mathscr M_z) \cap \mathbb D^2 = \emptyset $
(see [Reference Curto11, Theorem 5(c)]), by Lemma 5.1, Gleason’s problem can be solved for
![]() $H^2(\mathbb D^2).$
$H^2(\mathbb D^2).$
The following lemma provides a situation in which the division property ensures a solution to Gleason’s problem.
Lemma 5.3 Let
![]() $\mathscr H$
be a reproducing kernel Hilbert space of complex-valued holomorphic functions on the unit bidisc
$\mathscr H$
be a reproducing kernel Hilbert space of complex-valued holomorphic functions on the unit bidisc
![]() $\mathbb D^2$
, and let
$\mathbb D^2$
, and let
![]() $w=(w_1, w_2) \in \mathbb D^2.$
Assume that
$w=(w_1, w_2) \in \mathbb D^2.$
Assume that
![]() $\mathscr H$
has the division property and
$\mathscr H$
has the division property and
![]() $\mathscr M_z=(\mathscr M_{z_1}, \mathscr M_{z_2})$
is a commuting pair on
$\mathscr M_z=(\mathscr M_{z_1}, \mathscr M_{z_2})$
is a commuting pair on
![]() $\mathscr H.$
If, for every
$\mathscr H.$
If, for every
![]() $f \in \mathscr H,$
either
$f \in \mathscr H,$
either
![]() $f(\cdot , w_2)$
or
$f(\cdot , w_2)$
or
![]() $f(w_1, \cdot )$
belongs to
$f(w_1, \cdot )$
belongs to
![]() $\mathscr H,$
then Gleason’s problem can be solved for
$\mathscr H,$
then Gleason’s problem can be solved for
![]() $\mathscr H$
over
$\mathscr H$
over
![]() $\{w\}.$
$\{w\}.$
Proof For
![]() $f \in \mathscr H,$
assume that
$f \in \mathscr H,$
assume that
![]() $f(w_1, \cdot ) \in \mathscr H.$
Thus
$f(w_1, \cdot ) \in \mathscr H.$
Thus
![]() $f-f(w_1, \cdot )\in \mathscr H.$
Hence, if
$f-f(w_1, \cdot )\in \mathscr H.$
Hence, if
![]() $h : \mathbb D^2 \rightarrow \mathbb C$
is a holomorphic function such that
$h : \mathbb D^2 \rightarrow \mathbb C$
is a holomorphic function such that
by the division property for
![]() $\mathscr H,$
we have
$\mathscr H,$
we have
![]() $h \in \mathscr H.$
Also, since
$h \in \mathscr H.$
Also, since
![]() $f(w_1, \cdot ) \in \mathscr H,$
one may argue as above to see that there exists
$f(w_1, \cdot ) \in \mathscr H,$
one may argue as above to see that there exists
![]() $k \in \mathscr H$
satisfying
$k \in \mathscr H$
satisfying
This, combined with (5.5), completes the proof in this case. Similarly, one can deal with the case in which
![]() $f(\cdot , w_2) \in \mathscr H.$
$f(\cdot , w_2) \in \mathscr H.$
We also need the following fact of independent interest.
Lemma 5.4 For every
![]() $f \in \mathcal D(\mu _1, \mu _2),$
the slice functions
$f \in \mathcal D(\mu _1, \mu _2),$
the slice functions
![]() $f(\cdot , 0)$
and
$f(\cdot , 0)$
and
![]() $f(0, \cdot )$
belong to
$f(0, \cdot )$
belong to
![]() $\mathcal D(\mu _1, \mu _2).$
Moreover, the mappings
$\mathcal D(\mu _1, \mu _2).$
Moreover, the mappings
![]() $f \mapsto f(\cdot , 0)$
and
$f \mapsto f(\cdot , 0)$
and
![]() $f \mapsto f(0, \cdot )$
from
$f \mapsto f(0, \cdot )$
from
![]() $\mathcal D(\mu _1, \mu _2)$
into itself are contractive homomorphisms.
$\mathcal D(\mu _1, \mu _2)$
into itself are contractive homomorphisms.
Proof If
![]() $f \in \mathcal D(\mu _1, \mu _2),$
then
$f \in \mathcal D(\mu _1, \mu _2),$
then
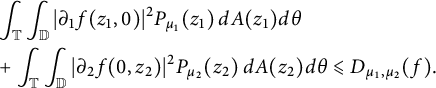 $$ \begin{align*} & \int_{\mathbb T} \int_{\mathbb D}|\partial_1 f(z_1, 0)|^2 P_{\mu_1}(z_1) \,dA(z_1)d\theta \\ &+ \int_{\mathbb T} \int_{\mathbb D}|\partial_2 f(0, z_2)|^2 P_{\mu_2}(z_2) \,dA(z_2)d\theta \leqslant D_{\mu_1, \mu_2}(f). \end{align*} $$
$$ \begin{align*} & \int_{\mathbb T} \int_{\mathbb D}|\partial_1 f(z_1, 0)|^2 P_{\mu_1}(z_1) \,dA(z_1)d\theta \\ &+ \int_{\mathbb T} \int_{\mathbb D}|\partial_2 f(0, z_2)|^2 P_{\mu_2}(z_2) \,dA(z_2)d\theta \leqslant D_{\mu_1, \mu_2}(f). \end{align*} $$
Since the mappings
![]() $f \mapsto f(\cdot , 0)$
and
$f \mapsto f(\cdot , 0)$
and
![]() $f \mapsto f(0, \cdot )$
from
$f \mapsto f(0, \cdot )$
from
![]() $H^2(\mathbb D^2)$
into itself are contractive homomorphisms, the desired conclusions may be deduced from the estimate above.
$H^2(\mathbb D^2)$
into itself are contractive homomorphisms, the desired conclusions may be deduced from the estimate above.
Proof (Proof of Theorem 2.3)
Since
![]() $\mathcal D(\mu _1, \mu _2)$
has the division property (see Theorem 2.2), by Lemmas 5.3 and 5.4, Gleason’s problem can be solved for
$\mathcal D(\mu _1, \mu _2)$
has the division property (see Theorem 2.2), by Lemmas 5.3 and 5.4, Gleason’s problem can be solved for
![]() $\mathcal{D}(\mu_1, \mu_2)$
over
$\mathcal{D}(\mu_1, \mu_2)$
over
![]() $\{(0, 0)\}.$
Hence, by Lemma 5.1 (which is applicable since
$\{(0, 0)\}.$
Hence, by Lemma 5.1 (which is applicable since
![]() $\mathscr M_z$
on
$\mathscr M_z$
on
![]() $\mathcal D(\mu _1, \mu _2)$
is cyclic; see Theorem 2.1),
$\mathcal D(\mu _1, \mu _2)$
is cyclic; see Theorem 2.1),
![]() $D^*_{\mathscr M^*_z}$
has closed range (see (5.1)). It is now easy to see using Corollaries 3.9 and 4.6 that
$D^*_{\mathscr M^*_z}$
has closed range (see (5.1)). It is now easy to see using Corollaries 3.9 and 4.6 that
![]() $\mathscr M_z$
is Fredholm. Since the essential spectrum is a closed subset of
$\mathscr M_z$
is Fredholm. Since the essential spectrum is a closed subset of
![]() $\mathbb C^2$
not containing
$\mathbb C^2$
not containing
![]() $(0, 0),$
there exists
$(0, 0),$
there exists
![]() $r> 0$
such that
$r> 0$
such that
![]() $\mathbb D^2_r \subseteq \mathbb C^2 \backslash \sigma _e(\mathscr M_z).$
Another application of Lemma 5.1 now completes the proof.
$\mathbb D^2_r \subseteq \mathbb C^2 \backslash \sigma _e(\mathscr M_z).$
Another application of Lemma 5.1 now completes the proof.
The following fact is implicit in the proof of Theorem 2.3.
Corollary 5.5 The commuting
![]() $2$
-tuple
$2$
-tuple
![]() $\mathscr M^*_z$
on
$\mathscr M^*_z$
on
![]() $\mathcal D(\mu _1, \mu _2)$
belongs to
$\mathcal D(\mu _1, \mu _2)$
belongs to
![]() $\mathbf {B}_1(\mathbb D^2_r)$
for some
$\mathbf {B}_1(\mathbb D^2_r)$
for some
![]() $r \in (0, 1].$
$r \in (0, 1].$
We conclude this section with the following corollary describing the cokernels of the multiplication operators
![]() $\mathscr M_{z_j}, j = 1, 2,$
on
$\mathscr M_{z_j}, j = 1, 2,$
on
![]() $\mathcal D(\mu _1, \mu _2).$
$\mathcal D(\mu _1, \mu _2).$
Corollary 5.6 For
![]() $1 \leqslant i \neq j \leqslant 2, \ker \mathscr M^*_{z_j} = \bigvee \big \{z^k_i : k \geqslant 0\big \}.$
$1 \leqslant i \neq j \leqslant 2, \ker \mathscr M^*_{z_j} = \bigvee \big \{z^k_i : k \geqslant 0\big \}.$
Proof As observed in the proof of Corollary 3.13,
To see the reverse inclusion, let
![]() $f \in \ker \mathscr M^*_{z_1}.$
By Theorem 2.1, there exists a sequence
$f \in \ker \mathscr M^*_{z_1}.$
By Theorem 2.1, there exists a sequence
![]() $\{p_n\}_{n \geqslant 1}$
of complex polynomials in
$\{p_n\}_{n \geqslant 1}$
of complex polynomials in
![]() $z_1, z_2$
converging to
$z_1, z_2$
converging to
![]() $f.$
By Lemma 5.4,
$f.$
By Lemma 5.4,
![]() $f(0, \cdot ) \in \mathcal D(\mu _1, \mu _2),$
and
$f(0, \cdot ) \in \mathcal D(\mu _1, \mu _2),$
and
![]() $\{p_n(0, \cdot )\}_{n \geqslant 1}$
converges to
$\{p_n(0, \cdot )\}_{n \geqslant 1}$
converges to
![]() $f(0, \cdot ).$
Hence, by (5.6),
$f(0, \cdot ).$
Hence, by (5.6),
![]() $f(0, \cdot ) \in \ker \mathscr M^*_{z_1}.$
Thus
$f(0, \cdot ) \in \ker \mathscr M^*_{z_1}.$
Thus
![]() $f-f(0, \cdot ) \in \ker \mathscr M^*_{z_1}.$
However, there exists a holomorphic function
$f-f(0, \cdot ) \in \ker \mathscr M^*_{z_1}.$
However, there exists a holomorphic function
![]() $h : \mathbb D^2 \rightarrow \mathbb C$
such that
$h : \mathbb D^2 \rightarrow \mathbb C$
such that
By Theorem 2.2, we have
![]() $h \in \mathcal D(\mu _1, \mu _2).$
It now follows from (5.7) that
$h \in \mathcal D(\mu _1, \mu _2).$
It now follows from (5.7) that
![]() $\mathscr M_{z_1}h \in \ker \mathscr M^*_{z_1}.$
Since
$\mathscr M_{z_1}h \in \ker \mathscr M^*_{z_1}.$
Since
![]() $\mathscr M^*_{z_1}\mathscr M_{z_1}$
is invertible, we must have
$\mathscr M^*_{z_1}\mathscr M_{z_1}$
is invertible, we must have
![]() $h=0,$
and hence, by (5.7),
$h=0,$
and hence, by (5.7),
![]() ${f=f(0, \cdot ),}$
or equivalently, f belongs to the closure of
${f=f(0, \cdot ),}$
or equivalently, f belongs to the closure of
![]() $\{p(z_2) : p \in \mathbb C[w]\}.$
Similarly, one can check that
$\{p(z_2) : p \in \mathbb C[w]\}.$
Similarly, one can check that
![]() $\ker \mathscr M^*_{z_2}$
is equal to the closure of
$\ker \mathscr M^*_{z_2}$
is equal to the closure of
![]() $\{p(z_1) : p \in \mathbb C[w]\}.$
$\{p(z_1) : p \in \mathbb C[w]\}.$
6 Proof of Theorem 2.4 and its consequences
The proof of Theorem 2.4 relies on revealing the structure of toral
![]() $2$
-isometries T with
$2$
-isometries T with
![]() $\ker T^*$
as a wandering subspace (see Definition 1.5).
$\ker T^*$
as a wandering subspace (see Definition 1.5).
Lemma 6.1 Let
![]() $T=(T_1, T_2)$
be a toral
$T=(T_1, T_2)$
be a toral
![]() $2$
-isometry. Then the following statements are true:
$2$
-isometry. Then the following statements are true:
-
(i) for any integers
 $k, l \geqslant 0,$
(6.1)
$k, l \geqslant 0,$
(6.1) $$ \begin{align} T^{*k}_1T^{*l}_2T^{l}_2T^{k}_1 & = T^{*k}_1T^{k}_1 + T^{*l}_2T^{l}_2 - I \\ \notag & = kT^*_1T_1+ lT^*_2T_2 -(k+l-1)I, \end{align} $$
$$ \begin{align} T^{*k}_1T^{*l}_2T^{l}_2T^{k}_1 & = T^{*k}_1T^{k}_1 + T^{*l}_2T^{l}_2 - I \\ \notag & = kT^*_1T_1+ lT^*_2T_2 -(k+l-1)I, \end{align} $$
-
(ii) for
 $f_0 \in \ker T^*,$
assume that (6.2)
$f_0 \in \ker T^*,$
assume that (6.2) $$ \begin{align} & \langle{T^m_1f_0},\,{T^p_1 T^q_2f_0} \rangle=0, \quad q \geqslant 1, m, p \geqslant 0, \end{align} $$
(6.3)Then we have the following
$$ \begin{align} & \langle{T^m_1f_0},\,{T^p_1 T^q_2f_0} \rangle=0, \quad q \geqslant 1, m, p \geqslant 0, \end{align} $$
(6.3)Then we have the following $$ \begin{align} & \langle{T^n_2f_0},\,{T^p_1 T^q_2f_0} \rangle=0, \quad p \geqslant 1, n, q \geqslant 0. \end{align} $$
$$ \begin{align} & \langle{T^n_2f_0},\,{T^p_1 T^q_2f_0} \rangle=0, \quad p \geqslant 1, n, q \geqslant 0. \end{align} $$
 $:$
$:$
 $$ \begin{align*} \langle{T^{m}_1T^n_2f_0},\,{T^{p}_1T^q_2f_0} \rangle = \begin{cases} 0, & \text{if}~ m\neq p, ~n \neq q, \\ \langle{T^n_2f_0},\,{T^q_2f_0} \rangle, & \text{if}~ m=p, ~n \neq q, \\ \langle{T^{m}_1f_0},\,{T^{p}_1f_0} \rangle, & \text{if}~ m \neq p, ~n = q, \\ \|T^{m}_1f_0\|^2 + \|T^n_2f_0\|^2 - \|f_0\|^2, & \text{if}~ m= p, ~n = q. \end{cases} \end{align*} $$
$$ \begin{align*} \langle{T^{m}_1T^n_2f_0},\,{T^{p}_1T^q_2f_0} \rangle = \begin{cases} 0, & \text{if}~ m\neq p, ~n \neq q, \\ \langle{T^n_2f_0},\,{T^q_2f_0} \rangle, & \text{if}~ m=p, ~n \neq q, \\ \langle{T^{m}_1f_0},\,{T^{p}_1f_0} \rangle, & \text{if}~ m \neq p, ~n = q, \\ \|T^{m}_1f_0\|^2 + \|T^n_2f_0\|^2 - \|f_0\|^2, & \text{if}~ m= p, ~n = q. \end{cases} \end{align*} $$
Proof (i) To see (6.1), we proceed by strong induction on
![]() $k+l, k, l \geqslant 0.$
Clearly, (6.1) holds for
$k+l, k, l \geqslant 0.$
Clearly, (6.1) holds for
![]() $0 \leqslant k+l \leqslant 1.$
Assume that (6.1) holds for integers
$0 \leqslant k+l \leqslant 1.$
Assume that (6.1) holds for integers
![]() $k,l \geqslant 0$
such that
$k,l \geqslant 0$
such that
![]() ${0 \leqslant k+l \leqslant n.}$
Note that for
${0 \leqslant k+l \leqslant n.}$
Note that for
![]() $k \geqslant 1$
and
$k \geqslant 1$
and
![]() $l \leqslant n-1,$
by the induction hypothesis,
$l \leqslant n-1,$
by the induction hypothesis,
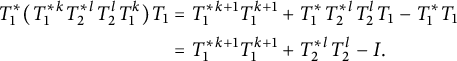 $$ \begin{align*} T^*_1(T^{*k}_1T^{*l}_2T^{l}_2T^{k}_1)T_1 &= T^{*k+1}_1T^{k+1}_1 + T^*_1T^{*l}_2T^{l}_2T_1 - T^*_1T_1 \\ &= T^{*k+1}_1T^{k+1}_1 + T^{*l}_2T^{l}_2 - I. \end{align*} $$
$$ \begin{align*} T^*_1(T^{*k}_1T^{*l}_2T^{l}_2T^{k}_1)T_1 &= T^{*k+1}_1T^{k+1}_1 + T^*_1T^{*l}_2T^{l}_2T_1 - T^*_1T_1 \\ &= T^{*k+1}_1T^{k+1}_1 + T^{*l}_2T^{l}_2 - I. \end{align*} $$
Similarly, for
![]() $k \leqslant n-1$
and
$k \leqslant n-1$
and
![]() $l \geqslant 1,$
(6.1) holds. This completes the induction argument. The remaining identity in (i) now follows from the known fact that for any
$l \geqslant 1,$
(6.1) holds. This completes the induction argument. The remaining identity in (i) now follows from the known fact that for any
![]() $2$
-isometry
$2$
-isometry
![]() $S,$
we have
$S,$
we have
(this known fact can be seen by induction on
![]() $k \geqslant 1$
).
$k \geqslant 1$
).
(ii) Let
![]() $m, n, p, q$
be integers such that
$m, n, p, q$
be integers such that
![]() $m \neq p$
and
$m \neq p$
and
![]() $n \neq q.$
Consider the case when
$n \neq q.$
Consider the case when
![]() $m < p$
and
$m < p$
and
![]() $n < q.$
Since
$n < q.$
Since
![]() $f_0 \in \ker T^*,$
we have
$f_0 \in \ker T^*,$
we have
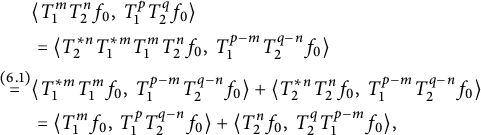 $$ \begin{align*} & \langle{T^m_1 T^n_2f_0},\,{T^p_1 T^q_2f_0} \rangle \\ & = \langle{T^{*n}_2 T^{*m}_1T^m_1 T^n_2f_0},\,{T^{p-m}_1 T^{q-n}_2f_0} \rangle \\ \overset{(6.1)}= & \langle{T^{*m}_1T^m_1 f_0},\,{T^{p-m}_1 T^{q-n}_2f_0} \rangle + \langle{T^{*n}_2 T^n_2f_0},\,{T^{p-m}_1 T^{q-n}_2f_0} \rangle \\ & = \langle{T^m_1 f_0},\,{T^{p}_1 T^{q-n}_2f_0} \rangle + \langle{T^n_2f_0},\,{T^{q}_2T^{p-m}_1 f_0} \rangle, \end{align*} $$
$$ \begin{align*} & \langle{T^m_1 T^n_2f_0},\,{T^p_1 T^q_2f_0} \rangle \\ & = \langle{T^{*n}_2 T^{*m}_1T^m_1 T^n_2f_0},\,{T^{p-m}_1 T^{q-n}_2f_0} \rangle \\ \overset{(6.1)}= & \langle{T^{*m}_1T^m_1 f_0},\,{T^{p-m}_1 T^{q-n}_2f_0} \rangle + \langle{T^{*n}_2 T^n_2f_0},\,{T^{p-m}_1 T^{q-n}_2f_0} \rangle \\ & = \langle{T^m_1 f_0},\,{T^{p}_1 T^{q-n}_2f_0} \rangle + \langle{T^n_2f_0},\,{T^{q}_2T^{p-m}_1 f_0} \rangle, \end{align*} $$
which, by (6.2) and (6.3), is equal to
![]() $0.$
Since the inner-product is conjugate linear,
$0.$
Since the inner-product is conjugate linear,
![]() $\langle {T^m_1 T^n_2f_0},\,{T^p_1 T^q_2f_0} \rangle =0$
when
$\langle {T^m_1 T^n_2f_0},\,{T^p_1 T^q_2f_0} \rangle =0$
when
![]() $p < m$
and
$p < m$
and
![]() $q < n.$
Consider the case when
$q < n.$
Consider the case when
![]() $m < p$
and
$m < p$
and
![]() $q < n.$
Arguing as above, we have
$q < n.$
Arguing as above, we have
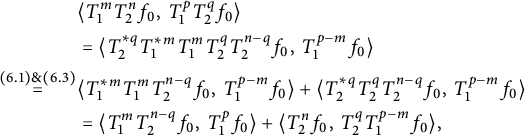 $$ \begin{align*} &\langle{T^m_1 T^n_2f_0},\,{T^p_1 T^q_2f_0} \rangle \\&= \langle{T^{*q}_2 T^{*m}_1T^m_1 T^{q}_2T^{n-q}_2f_0},\,{T^{p-m}_1 f_0} \rangle \\\overset{(6.1)\&(6.3)}=& \langle{T^{*m}_1T^m_1 T^{n-q}_2f_0},\,{T^{p-m}_1 f_0} \rangle + \langle{T^{*q}_2 T^{q}_2T^{n-q}_2f_0},\,{T^{p-m}_1 f_0} \rangle \\&= \langle{T^m_1 T^{n-q}_2f_0},\,{T^{p}_1 f_0} \rangle + \langle{T^{n}_2f_0},\,{T^{q}_2 T^{p-m}_1 f_0} \rangle, \end{align*} $$
$$ \begin{align*} &\langle{T^m_1 T^n_2f_0},\,{T^p_1 T^q_2f_0} \rangle \\&= \langle{T^{*q}_2 T^{*m}_1T^m_1 T^{q}_2T^{n-q}_2f_0},\,{T^{p-m}_1 f_0} \rangle \\\overset{(6.1)\&(6.3)}=& \langle{T^{*m}_1T^m_1 T^{n-q}_2f_0},\,{T^{p-m}_1 f_0} \rangle + \langle{T^{*q}_2 T^{q}_2T^{n-q}_2f_0},\,{T^{p-m}_1 f_0} \rangle \\&= \langle{T^m_1 T^{n-q}_2f_0},\,{T^{p}_1 f_0} \rangle + \langle{T^{n}_2f_0},\,{T^{q}_2 T^{p-m}_1 f_0} \rangle, \end{align*} $$
which, by (6.2) and (6.3), is equal to
![]() $0.$
Once again, by the conjugate-symmetry,
$0.$
Once again, by the conjugate-symmetry,
![]() $\langle {T^m_1 T^n_2 f_0},\,{T^p_1 T^q_2 f_0} \rangle =0$
when
$\langle {T^m_1 T^n_2 f_0},\,{T^p_1 T^q_2 f_0} \rangle =0$
when
![]() $p < m$
and
$p < m$
and
![]() $n < q.$
$n < q.$
If
![]() $m=p$
and
$m=p$
and
![]() $n \neq q,$
then one may argue as above using (6.4) (by making cases
$n \neq q,$
then one may argue as above using (6.4) (by making cases
![]() $n < q$
and
$n < q$
and
![]() $q < n$
) to show that
$q < n$
) to show that
![]() $\langle {T^m_1 T^n_2f_0},\,{T^p_1 T^q_2f_0} \rangle = \langle {T^n_2f_0},\,{T^q_2f_0} \rangle .$
Similarly, one may derived the formula in case of
$\langle {T^m_1 T^n_2f_0},\,{T^p_1 T^q_2f_0} \rangle = \langle {T^n_2f_0},\,{T^q_2f_0} \rangle .$
Similarly, one may derived the formula in case of
![]() $m \neq p$
and
$m \neq p$
and
![]() $n=q.$
Finally, if
$n=q.$
Finally, if
![]() $m=p$
and
$m=p$
and
![]() $n=q,$
then the formula follows from (6.1).
$n=q,$
then the formula follows from (6.1).
Proof (Proof of Theorem 2.4)
(i)
![]() $\Rightarrow $
(iii) Fix
$\Rightarrow $
(iii) Fix
![]() $j \in \{1, 2\}.$
Since T is analytic, so is
$j \in \{1, 2\}.$
Since T is analytic, so is
![]() $T_j.$
Thus
$T_j.$
Thus
![]() $T_j$
is an analytic
$T_j$
is an analytic
![]() $2$
-isometry. Consider the
$2$
-isometry. Consider the
![]() $T_j$
-invariant subspace
$T_j$
-invariant subspace
![]() $\mathcal H_j:=\bigvee \{T^k_j f_0 : k \geqslant 0\}$
and note that
$\mathcal H_j:=\bigvee \{T^k_j f_0 : k \geqslant 0\}$
and note that
![]() ${T_j}|_{\mathcal H_j}$
is a cyclic analytic
${T_j}|_{\mathcal H_j}$
is a cyclic analytic
![]() $2$
-isometry. Hence, by [Reference Richter26, Theorem 5.1], there exist a finite positive Borel measure
$2$
-isometry. Hence, by [Reference Richter26, Theorem 5.1], there exist a finite positive Borel measure
![]() $\mu _j$
on
$\mu _j$
on
![]() $\mathbb T$
and a unitary map
$\mathbb T$
and a unitary map
![]() $V_j : \mathcal H_j \rightarrow \mathcal D(\mu _j)$
such that
$V_j : \mathcal H_j \rightarrow \mathcal D(\mu _j)$
such that
where
![]() $\mathscr M^{(j)}_{w}$
denotes the operator of multiplication by the coordinate function w on
$\mathscr M^{(j)}_{w}$
denotes the operator of multiplication by the coordinate function w on
![]() $\mathcal D(\mu _j).$
We contend that the map given by
$\mathcal D(\mu _j).$
We contend that the map given by
extends to an unitary from
![]() $\mathcal H$
onto
$\mathcal H$
onto
![]() $\mathcal D(\mu _1, \mu _2).$
Since
$\mathcal D(\mu _1, \mu _2).$
Since
![]() $\mathcal H=\vee \{T^{k}_1T^l_2f_0 : k, l \geqslant 0\}$
and
$\mathcal H=\vee \{T^{k}_1T^l_2f_0 : k, l \geqslant 0\}$
and
![]() $\mathcal D(\mu _1, \mu _2)=\vee \{z^{k}_1z^l_2 : k, l \geqslant 0\},$
it suffices to check that
$\mathcal D(\mu _1, \mu _2)=\vee \{z^{k}_1z^l_2 : k, l \geqslant 0\},$
it suffices to check that
Note that for any integers
![]() $m, n \geqslant 0,$
by (6.5),
$m, n \geqslant 0,$
by (6.5),
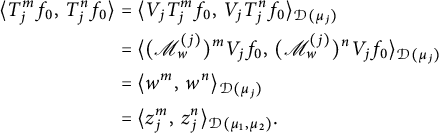 $$ \begin{align*} \langle{T^m_jf_0},\,{T^n_jf_0} \rangle&= \langle{V_j T^m_jf_0},\,{V_jT^n_jf_0} \rangle_{\mathcal D(\mu_j)} \\ &= \langle{(\mathscr M^{(j)}_{w})^{m}V_jf_0},\,{(\mathscr M^{(j)}_{w})^{n}V_jf_0} \rangle_{\mathcal D(\mu_j)} \\ &= \langle{w^m},\,{w^n} \rangle_{\mathcal D(\mu_j)} \\ &= \langle{z^m_j},\,{z^n_j} \rangle_{\mathcal D(\mu_1, \mu_2)}. \end{align*} $$
$$ \begin{align*} \langle{T^m_jf_0},\,{T^n_jf_0} \rangle&= \langle{V_j T^m_jf_0},\,{V_jT^n_jf_0} \rangle_{\mathcal D(\mu_j)} \\ &= \langle{(\mathscr M^{(j)}_{w})^{m}V_jf_0},\,{(\mathscr M^{(j)}_{w})^{n}V_jf_0} \rangle_{\mathcal D(\mu_j)} \\ &= \langle{w^m},\,{w^n} \rangle_{\mathcal D(\mu_j)} \\ &= \langle{z^m_j},\,{z^n_j} \rangle_{\mathcal D(\mu_1, \mu_2)}. \end{align*} $$
Since (6.2) and (6.3) hold (as
![]() $\ker T^*$
is a wandering subspace for T), combining this with Lemma 6.1(ii) yields (6.6), which completes the proof.
$\ker T^*$
is a wandering subspace for T), combining this with Lemma 6.1(ii) yields (6.6), which completes the proof.
(iii)
![]() $\Rightarrow $
(ii) This follows from Corollaries 3.8, 3.12, and 5.5.
$\Rightarrow $
(ii) This follows from Corollaries 3.8, 3.12, and 5.5.
(ii)
![]() $\Rightarrow $
(i) It suffices to check that T is analytic. By Oka–Grauert’s theorem (see [Reference Leiterer21, p. 71, Corollary 2.17], [Reference Eschmeier and Schmitt16, p. 3]), every holomorphic vector bundle on a bidisc is holomorphically trivial. Combining this with the proof of [Reference Eschmeier and Schmitt16, Theorem 4.5] shows that if
$\Rightarrow $
(i) It suffices to check that T is analytic. By Oka–Grauert’s theorem (see [Reference Leiterer21, p. 71, Corollary 2.17], [Reference Eschmeier and Schmitt16, p. 3]), every holomorphic vector bundle on a bidisc is holomorphically trivial. Combining this with the proof of [Reference Eschmeier and Schmitt16, Theorem 4.5] shows that if
![]() $T^* \in \mathbf {B}_1(\mathbb D^2_r),$
then T is unitarily equivalent to the multiplication
$T^* \in \mathbf {B}_1(\mathbb D^2_r),$
then T is unitarily equivalent to the multiplication
![]() $2$
-tuple
$2$
-tuple
![]() $\mathscr M_z$
on a reproducing kernel Hilbert space of scalar-valued holomorphic functions on
$\mathscr M_z$
on a reproducing kernel Hilbert space of scalar-valued holomorphic functions on
![]() $\mathbb D^2_r.$
Since
$\mathbb D^2_r.$
Since
![]() $\mathscr M_z$
is analytic, T is analytic.
$\mathscr M_z$
is analytic, T is analytic.
The conclusion of Theorem 2.4 can be rephrased as follows.
Corollary 6.2 A cyclic analytic toral
![]() $2$
-isometric
$2$
-isometric
![]() $2$
-tuple on
$2$
-tuple on
![]() $\mathcal H$
is unitarily equivalent to the multiplication pair
$\mathcal H$
is unitarily equivalent to the multiplication pair
![]() $\mathscr M_z$
on
$\mathscr M_z$
on
![]() $\mathcal D(\mu _1, \mu _2)$
if and only if
$\mathcal D(\mu _1, \mu _2)$
if and only if
![]() $\ker T^*$
is wandering subspace for T spanned by a cyclic vector for
$\ker T^*$
is wandering subspace for T spanned by a cyclic vector for
![]() $T.$
$T.$
Remark 6.3 Let
![]() $\mathcal D$
denote the Dirichlet space (that is, the Dirichlet-type space associated with the Lebesgue measure on the unit circle), and let
$\mathcal D$
denote the Dirichlet space (that is, the Dirichlet-type space associated with the Lebesgue measure on the unit circle), and let
![]() $\mathscr M_w$
be the operator of multiplication by w on
$\mathscr M_w$
be the operator of multiplication by w on
![]() $\mathcal D$
. It is easy to see that the commuting pair
$\mathcal D$
. It is easy to see that the commuting pair
![]() $T=(\mathscr M_w, \mathscr M_w)$
is a cyclic analytic toral
$T=(\mathscr M_w, \mathscr M_w)$
is a cyclic analytic toral
![]() $2$
-isometry on
$2$
-isometry on
![]() $\mathcal D.$
Note that
$\mathcal D.$
Note that
![]() $\ker T^*=\ker \mathscr M^*_w$
is spanned by
$\ker T^*=\ker \mathscr M^*_w$
is spanned by
![]() $1$
and it is not a wandering subspace for
$1$
and it is not a wandering subspace for
![]() $T.$
It is evident that T is not unitarily equivalent to the multiplication pair
$T.$
It is evident that T is not unitarily equivalent to the multiplication pair
![]() $\mathscr M_z$
on
$\mathscr M_z$
on
![]() $\mathcal D(\mu _1, \mu _2)$
for any
$\mathcal D(\mu _1, \mu _2)$
for any
![]() $\mu _1, \mu _2 \in M_+(\mathbb T).$
$\mu _1, \mu _2 \in M_+(\mathbb T).$
The following is a
![]() $2$
-variable analog of [Reference Richter26, Theorem 5.2].
$2$
-variable analog of [Reference Richter26, Theorem 5.2].
Theorem 6.4 For
![]() $j=1, 2,$
let
$j=1, 2,$
let
![]() $\mu ^{(j)}_1, \mu ^{(j)}_2 \in M_+(\mathbb T).$
Then the multiplication
$\mu ^{(j)}_1, \mu ^{(j)}_2 \in M_+(\mathbb T).$
Then the multiplication
![]() $2$
-tuple
$2$
-tuple
![]() $\mathscr M^{(1)}_{z}$
on
$\mathscr M^{(1)}_{z}$
on
![]() $\mathcal D(\mu ^{(1)}_1, \mu ^{(1)}_2)$
is unitarily equivalent to the multiplication
$\mathcal D(\mu ^{(1)}_1, \mu ^{(1)}_2)$
is unitarily equivalent to the multiplication
![]() $2$
-tuple
$2$
-tuple
![]() $\mathscr M^{(2)}_z$
on
$\mathscr M^{(2)}_z$
on
![]() $\mathcal D(\mu ^{(2)}_1, \mu ^{(2)}_2)$
if and only if
$\mathcal D(\mu ^{(2)}_1, \mu ^{(2)}_2)$
if and only if
![]() $\mu ^{(1)}_j = \mu ^{(2)}_j, j=1, 2.$
$\mu ^{(1)}_j = \mu ^{(2)}_j, j=1, 2.$
Proof Suppose there is a unitary operator
![]() $U : \mathcal D(\mu ^{(1)}_1, \mu ^{(1)}_2) \rightarrow \mathcal D(\mu ^{(2)}_1, \mu ^{(2)}_2)$
such that
$U : \mathcal D(\mu ^{(1)}_1, \mu ^{(1)}_2) \rightarrow \mathcal D(\mu ^{(2)}_1, \mu ^{(2)}_2)$
such that
Since the joint kernel of the adjoint of multiplication tuples is spanned by
![]() $1,$
by (6.7), U must map
$1,$
by (6.7), U must map
![]() $1$
to some constant of modulus
$1$
to some constant of modulus
![]() $1.$
After multiplying U by a unimodular constant, if required, we may assume that
$1.$
After multiplying U by a unimodular constant, if required, we may assume that
![]() $U1=1.$
It now follows from (6.7) that U is identity on polynomials. By Lemma 3.5 (applied twice), we obtain for any polynomial p in two variables,
$U1=1.$
It now follows from (6.7) that U is identity on polynomials. By Lemma 3.5 (applied twice), we obtain for any polynomial p in two variables,
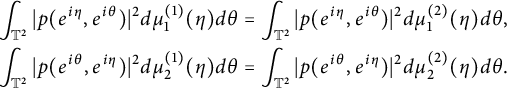 $$ \begin{align*} \int_{\mathbb T^2} |p(e^{i \eta}, e^{i \theta})|^2 d\mu^{(1)}_1(\eta)d\theta &= \int_{\mathbb T^2} |p(e^{i \eta}, e^{i \theta})|^2 d\mu^{(2)}_1(\eta)d\theta, \\ \int_{\mathbb T^2} |p(e^{i \theta}, e^{i \eta})|^2 d\mu^{(1)}_2(\eta)d\theta &= \int_{\mathbb T^2} |p(e^{i \theta}, e^{i \eta})|^2 d\mu^{(2)}_2(\eta)d\theta. \end{align*} $$
$$ \begin{align*} \int_{\mathbb T^2} |p(e^{i \eta}, e^{i \theta})|^2 d\mu^{(1)}_1(\eta)d\theta &= \int_{\mathbb T^2} |p(e^{i \eta}, e^{i \theta})|^2 d\mu^{(2)}_1(\eta)d\theta, \\ \int_{\mathbb T^2} |p(e^{i \theta}, e^{i \eta})|^2 d\mu^{(1)}_2(\eta)d\theta &= \int_{\mathbb T^2} |p(e^{i \theta}, e^{i \eta})|^2 d\mu^{(2)}_2(\eta)d\theta. \end{align*} $$
It is easy to see that for any polynomial p in one variable,
Combining polarization identity with the uniqueness of the trigonometric moment problem yields the desired uniqueness.
Remark 6.5 One may use Lemma 3.5 and argue as in [Reference Richter26, Theorem 6.2] to obtain the following fact: For
![]() $j=1, 2,$
let
$j=1, 2,$
let
![]() $\mu ^{(j)}_1, \mu ^{(j)}_2 \in M_+(\mathbb T).$
Then
$\mu ^{(j)}_1, \mu ^{(j)}_2 \in M_+(\mathbb T).$
Then
if and only if
![]() $\mu ^{(2)}_j \ll \mu ^{(1)}_j$
and the Radon–Nikodým derivative
$\mu ^{(2)}_j \ll \mu ^{(1)}_j$
and the Radon–Nikodým derivative
![]() ${d\mu ^{(2)}_j}/{d\mu ^{(1)}_j} \in L^\infty (\mathbb T), j=1, 2.$
We leave the details to the reader.
${d\mu ^{(2)}_j}/{d\mu ^{(1)}_j} \in L^\infty (\mathbb T), j=1, 2.$
We leave the details to the reader.
We conclude this section with an application to toral isometries.
Corollary 6.6 Let
![]() $T=(T_1, T_2)$
be a cyclic analytic toral isometry with cyclic vector
$T=(T_1, T_2)$
be a cyclic analytic toral isometry with cyclic vector
![]() $f_0 \in \ker T^*.$
Then the following statements are equivalent:
$f_0 \in \ker T^*.$
Then the following statements are equivalent:
-
(i)
 $\ker T^*$
is a wandering subspace for
$\ker T^*$
is a wandering subspace for
 $T,$
$T,$
-
(ii) T is unitarily equivalent to
 $\mathscr M_z$
on
$\mathscr M_z$
on
 $H^2(\mathbb D^2),$
$H^2(\mathbb D^2),$
-
(iii) T is doubly commuting, that is,
 $T^*_{j}T_{i}=T_{i}T^*_{j}, 1 \leqslant i \neq j \leqslant 2.$
$T^*_{j}T_{i}=T_{i}T^*_{j}, 1 \leqslant i \neq j \leqslant 2.$
Proof (i)
![]() $\Rightarrow $
(ii) By Theorem 2.4, there exist
$\Rightarrow $
(ii) By Theorem 2.4, there exist
![]() $\mu _1, \mu _2 \in M_+(\mathbb T)$
such that T is unitarily equivalent to
$\mu _1, \mu _2 \in M_+(\mathbb T)$
such that T is unitarily equivalent to
![]() $\mathscr M_z$
on
$\mathscr M_z$
on
![]() $\mathcal D(\mu _1, \mu _2).$
Since T is a toral isometry,
$\mathcal D(\mu _1, \mu _2).$
Since T is a toral isometry,
![]() $\mathscr M_z$
is also a toral isometry. It now follows from (2.1) that for every polynomial p in two variables,
$\mathscr M_z$
is also a toral isometry. It now follows from (2.1) that for every polynomial p in two variables,
One may now argue as in the proof of Theorem 6.4 to conclude that
![]() $\mu _1=0$
and
$\mu _1=0$
and
![]() $\mu _2=0.$
This yields (ii).
$\mu _2=0.$
This yields (ii).
The implication (ii)
![]() $\Rightarrow $
(iii) is a routine verification, while the implication (iii)
$\Rightarrow $
(iii) is a routine verification, while the implication (iii)
![]() $\Rightarrow $
(i) is recorded in Remark 1.6.
$\Rightarrow $
(i) is recorded in Remark 1.6.
7 Concluding remarks
We conclude the paper with a brief discussion on the spectral picture of the multiplication
![]() $2$
-tuple
$2$
-tuple
![]() $\mathscr M_z$
on
$\mathscr M_z$
on
![]() $\mathcal D(\mu _1, \mu _2).$
We claim that
$\mathcal D(\mu _1, \mu _2).$
We claim that
for some open set
![]() $\Omega $
in
$\Omega $
in
![]() $\mathbb C^2$
containing
$\mathbb C^2$
containing
![]() $\big (\mathbb D \times \{0\}\big ) \cup \big (\{0\} \times \mathbb D\big ).$
To see (7.1), note that by [Reference Curto, Conway and Morrel12, Theorem 4.9], for any commuting pair
$\big (\mathbb D \times \{0\}\big ) \cup \big (\{0\} \times \mathbb D\big ).$
To see (7.1), note that by [Reference Curto, Conway and Morrel12, Theorem 4.9], for any commuting pair
![]() $T=(T_1, T_2), \sigma (T) \subseteq \sigma (T_1) \times \sigma (T_2).$
Since the spectrum of any
$T=(T_1, T_2), \sigma (T) \subseteq \sigma (T_1) \times \sigma (T_2).$
Since the spectrum of any
![]() $2$
-isometry is contained in
$2$
-isometry is contained in
![]() $\overline {\mathbb D}$
(see [Reference Agler and Stankus2, Lemma 1.21]) and both
$\overline {\mathbb D}$
(see [Reference Agler and Stankus2, Lemma 1.21]) and both
![]() $\mathscr M_{z_1}$
and
$\mathscr M_{z_1}$
and
![]() $\mathscr M_{z_2}$
are
$\mathscr M_{z_2}$
are
![]() $2$
-isometries (see Corollary 3.8), we obtain
$2$
-isometries (see Corollary 3.8), we obtain
![]() $ \sigma (\mathscr M_z) \subseteq \overline {\mathbb D}^2.$
Also, by Corollary 3.9,
$ \sigma (\mathscr M_z) \subseteq \overline {\mathbb D}^2.$
Also, by Corollary 3.9,
![]() $\mathbb D^2 \subseteq \sigma _p(\mathscr M^*_z) \subseteq \sigma (\mathscr M^*_z).$
Since
$\mathbb D^2 \subseteq \sigma _p(\mathscr M^*_z) \subseteq \sigma (\mathscr M^*_z).$
Since
![]() $\sigma (\mathscr M^*_z)=\{\overline {z} : z \in \sigma (\mathscr M_z)\},$
we have the inclusion
$\sigma (\mathscr M^*_z)=\{\overline {z} : z \in \sigma (\mathscr M_z)\},$
we have the inclusion
![]() $\mathbb D^2 \subseteq \sigma (\mathscr M_z).$
Finally, since the Taylor spectrum is closed (see [Reference Curto, Conway and Morrel12, Corollary 4.2]), we obtain (7.1). On the other hand, an examination of the proof of Theorem 2.3 (using the full power of Lemma 5.3 together with Lemma 5.4) shows that
$\mathbb D^2 \subseteq \sigma (\mathscr M_z).$
Finally, since the Taylor spectrum is closed (see [Reference Curto, Conway and Morrel12, Corollary 4.2]), we obtain (7.1). On the other hand, an examination of the proof of Theorem 2.3 (using the full power of Lemma 5.3 together with Lemma 5.4) shows that
Since the essential spectrum is a closed subset of the Taylor spectrum, (7.2) now follows from (7.1). The natural question arises whether the unit bidisc lies in the complement of the essential spectrum of
![]() $\mathscr M_z$
(there are interesting examples of toral
$\mathscr M_z$
(there are interesting examples of toral
![]() $2$
-isometries supporting this possibility; see [Reference Athavale and Sholapurkar5, Proposition 5(iii)]). If this question has an affirmative answer, then
$2$
-isometries supporting this possibility; see [Reference Athavale and Sholapurkar5, Proposition 5(iii)]). If this question has an affirmative answer, then
![]() $\sigma _e(\mathscr M_z) = \partial (\mathbb D^2).$
Indeed, if
$\sigma _e(\mathscr M_z) = \partial (\mathbb D^2).$
Indeed, if
![]() $\lambda \in \partial (\mathbb D^2) \backslash \sigma _e(\mathscr M_z),$
then there exist two sequences in
$\lambda \in \partial (\mathbb D^2) \backslash \sigma _e(\mathscr M_z),$
then there exist two sequences in
![]() $\mathbb D^2$
and
$\mathbb D^2$
and
![]() $\mathbb C^2 \backslash \overline {\mathbb D}^2$
converging to
$\mathbb C^2 \backslash \overline {\mathbb D}^2$
converging to
![]() $\lambda ,$
which together with the continuity of the Fredholm index (see (4.7)) leads to a contradiction. This in turn leads to an improvement of Corollary 5.5 providing a bidisc analog of [Reference Richter26, Corollary 3.8] and also solves Gleason’s problem for
$\lambda ,$
which together with the continuity of the Fredholm index (see (4.7)) leads to a contradiction. This in turn leads to an improvement of Corollary 5.5 providing a bidisc analog of [Reference Richter26, Corollary 3.8] and also solves Gleason’s problem for
![]() $\mathcal D(\mu _1, \mu _2)$
(see Lemma 5.1).
$\mathcal D(\mu _1, \mu _2)$
(see Lemma 5.1).
Acknowledgment
The authors would like to thank Archana Morye, Shibananda Biswas, and Somnath Hazra for some fruitful conversations on the subject of this article.