Hostname: page-component-848d4c4894-4hhp2 Total loading time: 0 Render date: 2024-06-01T18:59:32.949Z Has data issue: false hasContentIssue false
  • English
  • Français

On an Enriques Surface Associated With a Quartic Hessian Surface

Part of: Surfaces and higher-dimensional varieties Computational aspects in algebraic geometry

Published online by Cambridge University Press:  09 January 2019

Ichiro Shimada
Ichiro Shimada*
Affiliation:
Division of Mathematics, Graduate School of Science, Hiroshima University, 1-3-1 Kagamiyama, Higashi-Hiroshima, 739-8526, Japan Email: ichiro-shimada@hiroshima-u.ac.jp
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 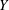$Y$ be a complex Enriques surface whose universal cover 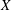$X$ is birational to a general quartic Hessian surface. Using the result on the automorphism group of 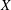$X$ due to Dolgachev and Keum, we obtain a finite presentation of the automorphism group of 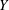$Y$. The list of elliptic fibrations on 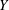$Y$ and the list of combinations of rational double points that can appear on a surface birational to 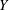$Y$ are presented. As an application, a set of generators of the automorphism group of the generic Enriques surface is calculated explicitly.

Keywords

Enriques surfaceK3 surfaceautomorphismlattice

MSC classification

Primary: 14J28: $K3$ surfaces and Enriques surfaces
Secondary: 14Q10: Surfaces, hypersurfaces
Type
Article
Information
Canadian Journal of Mathematics , Volume 71 , Issue 1 , February 2019 , pp. 213 - 246
Copyright
© Canadian Mathematical Society 2018 

Footnotes

This work was supported by JSPS KAKENHI Grant Number 16H03926 and 16K13749.

References

Conway, J. H., Curtis, R. T., Norton, S. P., Parker, R. A., and Wilson, R. A., Atlas of finite groups. Oxford University Press, Eynsham, 1985.Google Scholar
Barth, W. and Peters, C., Automorphisms of Enriques surfaces . Invent. Math. 73(1983), no. 3, 383–411. https://doi.org/10.1007/BF01388435.Google Scholar
Borcherds, Richard, Automorphism groups of Lorentzian lattices . J. Algebra 111(1987), no. 1, 133–153. https://doi.org/10.1016/0021-8693(87)90245-6.Google Scholar
Borcherds, Richard, Coxeter groups, Lorentzian lattices, and K3 surfaces . Internat. Math. Res. Notices(1998), no. 19, 1011–1031. https://doi.org/10.1155/S1073792898000609.Google Scholar
Conway, J. H., The automorphism group of the 26-dimensional even unimodular Lorentzian lattice . J. Algebra 80(1983), no. 1, 159–163. https://doi.org/10.1016/0021-8693(83)90025-X.Google Scholar
Dardanelli, Elisa and van Geemen, Bert, Hessians and the moduli space of cubic surfaces. In: Algebraic geometry. Contemp. Math., 422. Amer. Math. Soc., Providence, RI, 2007, pp. 17–36. https://doi.org/10.1090/conm/422/08054.Google Scholar
Dolgachev, Igor, Salem numbers and Enriques surfaces . Exp. Math. 27(2018), 287–301. https://doi.org/10.1080/10586458.2016.1261743.Google Scholar
Dolgachev, Igor and Keum, Jonghae, Birational automorphisms of quartic Hessian surfaces . Trans. Amer. Math. Soc. 354(2002), no. 8, 3031–3057. https://doi.org/10.1090/S0002-9947-02-03011-8.Google Scholar
Ebeling, Wolfgang, Lattices and codes. Advanced Lectures in Mathematics. Third edition. Springer Spektrum, Wiesbaden 2013. https://doi.org/10.1007/978-3-658-00360-9.Google Scholar
The GAP Group, GAP - Groups, Algorithms, and Programming. Version 4.7.9; 2015 http://www.gap-system.org.Google Scholar
Katsura, Toshiyuki, Kondo, Shigeyuki, and Shimada, Ichiro, On the supersingular K3 surface in characteristic 5 with Artin invariant 1 . Michigan Math. J. 63(2014), no. 4, 803–844. https://doi.org/10.1307/mmj/1417799227.Google Scholar
Keum, Jonghae, Every algebraic Kummer surface is the K3-cover of an Enriques surface . Nagoya Math. J. 118(1990), 99–110. https://doi.org/10.1017/S0027763000003019.Google Scholar
Koike, Kenji, Hessian K3 surfaces of non-Sylvester type . J. Algebra 330(2011), 388–403. https://doi.org/10.1016/j.jalgebra.2010.12.006.Google Scholar
Kondō, Shigeyuki, Enriques surfaces with finite automorphism groups . Japan. J. Math. (N.S.) 12(1986), no. 2, 191–282. https://doi.org/10.4099/math1924.12.191.Google Scholar
Kondō, Shigeyuki, The automorphism group of a generic Jacobian Kummer surface . J. Algebraic Geom. 7(1998), no. 3, 589–609.Google Scholar
Kondō, Shigeyuki, The moduli space of Hessian quartic surfaces and automorphic forms . J. Pure Appl. Algebra 216(2012), no. 10, 2233–2240. https://doi.org/10.1016/j.jpaa.2012.02.001.Google Scholar
Magnus, Wilhelm, Karrass, Abraham, and Solitar, Donald, Combinatorial group theory. Second edition. Dover Publications, Mineola, NY, 2004.Google Scholar
McMullen, Curtis T., Automorphisms of projective K3 surfaces with minimum entropy . Invent. Math. 203(2016), no. 1, 179–215.Google Scholar
Mukai, Shigeru, Numerically trivial involutions of Kummer type of an Enriques surface . Kyoto J. Math. 50(2010), no. 4, 889–902. https://doi.org/10.1215/0023608X-2010-017.Google Scholar
Mukai, Shigeru and Namikawa, Yukihiko, Automorphisms of Enriques surfaces which act trivially on the cohomology groups . Invent. Math. 77(1984), no. 3, 383–397. https://doi.org/10.1007/BF01388829.Google Scholar
Mukai, S. and Ohashi, H., The automorphism groups of Enriques surfaces covered by symmetric quartic surfaces . In: Recent advances in algebraic geometry. London Math. Soc. Lecture Note Ser., 417. Cambridge Univ. Press, Cambridge, 2015, pp. 307–320.Google Scholar
Nikulin, V. V., Integer symmetric bilinear forms and some of their geometric applications . Izv. Akad. Nauk SSSR Ser. Mat. 43(1979), no. 1, 111–177, 238.Google Scholar
Nikulin, V. V., Description of automorphism groups of Enriques surfaces . Dokl. Akad. Nauk SSSR 277(1984), no. 6, 1324–1327.Google Scholar
Oguiso, Keiji, The third smallest Salem number in automorphisms of K3 surfaces. Adv. Stud. Pure Math., 60. Math. Soc. Japan, Tokyo, 2010, pp. 331–360. https://doi.org/10.1142/e031.Google Scholar
Piatetski-Shapiro, I. I. and Shafarevich, I. R., Torelli’s theorem for algebraic surfaces of type K3 . Izv. Akad. Nauk SSSR Ser. Mat. 35(1971), 530–572. Reprinted in I. R. Shafarevich, Collected Mathematical Papers, Springer-Verlag, Berlin, 1989, pp. 516–557.Google Scholar
Shimada, Ichiro, Projective models of the supersingular K3 surface with Artin invariant 1 in characteristic 5 . J. Algebra 403(2014), 273–299. https://doi.org/10.1016/j.jalgebra.2013.12.029.Google Scholar
Shimada, Ichiro, An algorithm to compute automorphism groups of K3 surfaces and an application to singular K3 surfaces . Int. Math. Res. Not. IMRN(2015), no. 22, 11961–12014.Google Scholar
Shimada, Ichiro, Holes of the Leech lattice and the projective models of K3 surfaces . Math. Proc. Cambridge Philos. Soc. 163(2017), 125–143. https://doi.org/10.1017/S030500411600075X.Google Scholar
Shimada, Ichiro, The automorphism groups of certain singular K3 surfaces and an Enriques surface . In: K3 surfaces and their moduli. Progr. Math., 315. Birkhäuser/Springer, Basel, 2016, pp. 297–343. https://doi.org/10.1007/978-3-319-29959-4_12.Google Scholar
Shimada, Ichiro, Rational double points on Enriques surfaces, 2017. arxiv:1710.01461.Google Scholar
Shimada, Ichiro, On an Enriques surface associated with a quartic Hessian surface: computational data, 2016. http://www.math.sci.hiroshima-u.ac.jp/∼shimada/K3andEnriques.html.Google Scholar
Vinberg, È. B., Some arithmetical discrete groups in Lobačevskiıi spaces . In: Discrete subgroups of Lie groups and applications to moduli. Oxford Univ. Press, Bombay, 1975, pp. 323–348.Google Scholar