Contents
Research Article
Weierstrass Points at the Cusps of Γ0(16p) and Hyperellipticity of Γ0(n)
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 960-968
-
- Article
-
- You have access
- Export citation
Extreme Points in the Hardy Class H 1 of a Riemann Surface
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 969-976
-
- Article
-
- You have access
- Export citation
Obstructions to Liftings in Commutative Squares
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 977-982
-
- Article
-
- You have access
- Export citation
Isomorphic Subgroups of Finite p-Groups. I
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 983-1022
-
- Article
-
- You have access
- Export citation
Isomorphic Subgroups of Finite p-Groups. II
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1023-1039
-
- Article
-
- You have access
- Export citation
Fundamental Biorthogonal Sequences and K-Norms on ϕ
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1040-1050
-
- Article
-
- You have access
- Export citation
Normed Linear Spaces that are Uniformly Convex in Every Direction
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1051-1059
-
- Article
-
- You have access
- Export citation
On Unitary Polarities of Finite Projective Planes
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1060-1077
-
- Article
-
- You have access
- Export citation
Mercerian Conditions for the Method (F, dn )
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1078-1085
-
- Article
-
- You have access
- Export citation
Correction
Existence Theorems for Some Nonlinear Equations of Evolution*: Corrigendum
-
- Published online by Cambridge University Press:
- 20 November 2018, p. 1086
-
- Article
-
- You have access
- Export citation
Research Article
On Screenability and Metrizability of Moore Spaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1087-1092
-
- Article
-
- You have access
- Export citation
Correction
Approximation By Unimodular Functions: Corrigendum
-
- Published online by Cambridge University Press:
- 20 November 2018, p. 1093
-
- Article
-
- You have access
- Export citation
Research Article
Injective Hulls of Torsion Free Modules
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1094-1101
-
- Article
-
- You have access
- Export citation
Immersions and Embeddings Up to Cobordism
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1102-1115
-
- Article
-
- You have access
- Export citation
Pseudo Harmonic Measures and the Dirichlet Problem
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1116-1120
-
- Article
-
- You have access
- Export citation
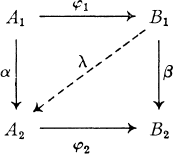
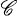
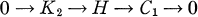
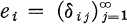 and
and  of order
of order 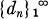 be a complex sequence with
be a complex sequence with