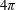Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Kalvin, Victor
2021.
Polyakov-Alvarez type comparison formulas for determinants of Laplacians on Riemann surfaces with conical singularities.
Journal of Functional Analysis,
Vol. 280,
Issue. 7,
p.
108866.
Kalvin, Victor
2023.
Determinants of Laplacians for constant curvature metrics with three conical singularities on the 2-sphere.
Calculus of Variations and Partial Differential Equations,
Vol. 62,
Issue. 2,