No CrossRef data available.
Article contents
On the Smallest and Largest Zeros of Müntz-Legendre Polynomials
Published online by Cambridge University Press: 20 November 2018
Abstract
Müntz-Legendre polynomials 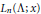 ${{L}_{n}}\left( \Lambda ;\,x \right)$ associated with a sequence
${{L}_{n}}\left( \Lambda ;\,x \right)$ associated with a sequence 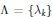 $\Lambda \,=\,\left\{ {{\lambda }_{k}} \right\}$ are obtainedby orthogonalizing the system
$\Lambda \,=\,\left\{ {{\lambda }_{k}} \right\}$ are obtainedby orthogonalizing the system 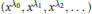 $\left( {{x}^{{{\lambda }_{0}}}},{{x}^{{{\lambda }_{1}}}},{{x}^{{{\lambda }_{2}}}},... \right)$ in
$\left( {{x}^{{{\lambda }_{0}}}},{{x}^{{{\lambda }_{1}}}},{{x}^{{{\lambda }_{2}}}},... \right)$ in 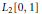 ${{L}_{2}}\left[ 0,1 \right]$ with respect to the Legendre weight. Ifthe
${{L}_{2}}\left[ 0,1 \right]$ with respect to the Legendre weight. Ifthe 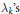 ${{\lambda }_{k}}\text{ }\!\!'\!\!\text{ s}$ are distinct, it is well known that
${{\lambda }_{k}}\text{ }\!\!'\!\!\text{ s}$ are distinct, it is well known that 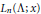 ${{L}_{n}}\left( \Lambda ;\,x \right)$ has exactly
${{L}_{n}}\left( \Lambda ;\,x \right)$ has exactly  $n$ zeros
$n$ zeros 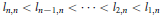 ${{l}_{n,n}}\,<\,{{l}_{n-1,n}}\,<\,\cdot \cdot \cdot \,<\,{{l}_{2,n}}\,<\,{{l}_{1,n}}$ on
${{l}_{n,n}}\,<\,{{l}_{n-1,n}}\,<\,\cdot \cdot \cdot \,<\,{{l}_{2,n}}\,<\,{{l}_{1,n}}$ on 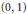 $\left( 0,1 \right)$ .
$\left( 0,1 \right)$ .
First we prove the following global bound for the smallest zero,
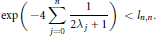 $$\exp \left( -4\sum\limits_{j=0}^{n}{\frac{1}{2\text{ }\!\!\lambda\!\!\text{ j}\,\text{+}\,\text{1}}} \right)\,<\,{{l}_{n,n}}.$$
$$\exp \left( -4\sum\limits_{j=0}^{n}{\frac{1}{2\text{ }\!\!\lambda\!\!\text{ j}\,\text{+}\,\text{1}}} \right)\,<\,{{l}_{n,n}}.$$
An important consequence is that if the associated Müntz space is non-dense in 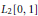 ${{L}_{2}}\left[ 0,1 \right]$ , then
${{L}_{2}}\left[ 0,1 \right]$ , then
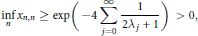 $$\underset{n}{\mathop{\inf }}\,\,{{x}_{n,n}}\,\ge \,\exp \,\left( -4\,\sum\limits_{j=0}^{\infty }{\frac{1}{2{{\text{ }\!\!\lambda\!\!\text{ }}_{j}}\,+\,1}} \right)\,>\,0,$$
$$\underset{n}{\mathop{\inf }}\,\,{{x}_{n,n}}\,\ge \,\exp \,\left( -4\,\sum\limits_{j=0}^{\infty }{\frac{1}{2{{\text{ }\!\!\lambda\!\!\text{ }}_{j}}\,+\,1}} \right)\,>\,0,$$
so the elements 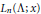 ${{L}_{n}}\left( \Lambda ;\,x \right)$ have no zeros close to 0.
${{L}_{n}}\left( \Lambda ;\,x \right)$ have no zeros close to 0.
Furthermore, we determine the asymptotic behavior of the largest zeros; for  $k$ fixed,
$k$ fixed,
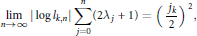 $$\underset{n\to \infty }{\mathop{\lim }}\,\,\left| \log \,{{l}_{k,n}} \right|\,\sum\limits_{j=0}^{n}{\left( 2{{\text{ }\!\!\lambda\!\!\text{ }}_{j}}\,+\,1 \right)}\,=\,{{\left( \frac{jk}{2} \right)}^{2}},$$
$$\underset{n\to \infty }{\mathop{\lim }}\,\,\left| \log \,{{l}_{k,n}} \right|\,\sum\limits_{j=0}^{n}{\left( 2{{\text{ }\!\!\lambda\!\!\text{ }}_{j}}\,+\,1 \right)}\,=\,{{\left( \frac{jk}{2} \right)}^{2}},$$
where 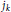 ${{j}_{k}}$ denotes the
${{j}_{k}}$ denotes the  $k$ -th zero of the Bessel function
$k$ -th zero of the Bessel function 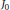 ${{J}_{0}}.$
${{J}_{0}}.$
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2013

