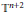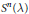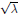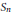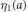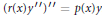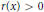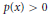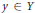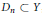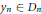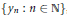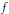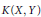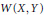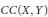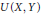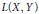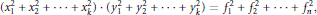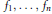Contents
Research Article
Semiclassical Limits of Eigenfunctions on Flat n-Dimensional Tori
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 3-12
-
- Article
-
- You have access
- Export citation
Ordering the Representations of
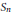 ${{S}_{n}}$ Using the Interchange Process
${{S}_{n}}$ Using the Interchange Process
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 13-30
-
- Article
-
- You have access
- Export citation
Derivations and Valuation Rings
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 31-38
-
- Article
-
- You have access
- Export citation
Comparison Theorem for Conjugate Points of a Fourth-order Linear Differential Equation
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 39-43
-
- Article
-
- You have access
- Export citation
Polystable Parabolic Principal G-Bundles and Hermitian-Einstein Connections
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 44-54
-
- Article
-
- You have access
- Export citation
Cliquishness and Quasicontinuity of Two-Variable Maps
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 55-64
-
- Article
-
- You have access
- Export citation
The Uncomplemented Subspace K(X,Y)
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 65-69
-
- Article
-
- You have access
- Export citation
An Asymptotic Bound on the Composition Number of Integer Sums of Squares Formulas
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 70-79
-
- Article
-
- You have access
- Export citation
Three Fixed Point Theorems: Periodic Solutions of a Volterra Type Integral Equation with Infinite Heredity
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 80-91
-
- Article
-
- You have access
- Export citation
On Perturbations of Continuous Maps
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 92-101
-
- Article
-
- You have access
- Export citation
Eigenvalue Approach to Even Order System Periodic Boundary Value Problems
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 102-115
-
- Article
-
- You have access
- Export citation
Central Extensions of Loop Groups and Obstruction to Pre-Quantization
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 116-126
-
- Article
-
- You have access
- Export citation
Evolution of Eigenvalues along Rescaled Ricci Flow
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 127-135
-
- Article
-
- You have access
- Export citation
On Constructing Ergodic Hyperfinite Equivalence Relations of Non-Product Type
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 136-147
-
- Article
-
- You have access
- Export citation
On the Gras Conjecture for Imaginary Quadratic Fields
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 148-160
-
- Article
-
- You have access
- Export citation
An Extension of the Dirichlet Density for Sets of Gaussian Integers
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 161-172
-
- Article
-
- You have access
- Export citation
Semi-invariant Submersions from Almost Hermitian Manifolds
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 173-183
-
- Article
-
- You have access
- Export citation
On Some Non-Riemannian Quantities in Finsler Geometry
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 184-193
-
- Article
-
- You have access
- Export citation
On the Smallest and Largest Zeros of Müntz-Legendre Polynomials
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 194-202
-
- Article
-
- You have access
- Export citation
Productively Lindelöf Spaces May All Be D
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 203-212
-
- Article
-
- You have access
- Export citation