Contents
Research Article
Completions of Ordered Sets
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 469-472
-
- Article
-
- You have access
- Export citation
The Laurent Expansion Without Cauchy's Integral Theorem
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 473-480
-
- Article
-
- You have access
- Export citation
On Sturm's Separation Theorem
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 481-487
-
- Article
-
- You have access
- Export citation
Integral Functionals in the Duals of Lλ-Spacesc(1)
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 489-499
-
- Article
-
- You have access
- Export citation
A Theorem in the Partition Calculus
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 501-505
-
- Article
-
- You have access
- Export citation
The Fixed Point Set of Real Multi-Valued Contraction Mappings
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 507-511
-
- Article
-
- You have access
- Export citation
Normal Variations of Invariant Hypersurfaces of Framed Manifolds
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 513-521
-
- Article
-
- You have access
- Export citation
Third-Engel 2-Groups are Soluble
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 523-524
-
- Article
-
- You have access
- Export citation
Summability Tests for Singular Points
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 525-528
-
- Article
-
- You have access
- Export citation
The Group of Units of the Integral Group Ring ZS3
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 529-534
-
- Article
-
- You have access
- Export citation
On a Question of Colin Clark Concerning Three Properties of Convex Sets(1)
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 535-537
-
- Article
-
- You have access
- Export citation
On the Finite Two-Dimensional Linear Groups II.(1)
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 539-546
-
- Article
-
- You have access
- Export citation
On Unbiased Estimation of a Vector Parameter
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 547-550
-
- Article
-
- You have access
- Export citation
Approximation of Functions by a Bernstein-Type Operator
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 551-557
-
- Article
-
- You have access
- Export citation
Local Malcev Conditions
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 559-568
-
- Article
-
- You have access
- Export citation
On the Frattini Subgroups of Generalized Free Products with Cyclic Amalgamations(1)
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 569-573
-
- Article
-
- You have access
- Export citation
Uniqueness of Compatible Quasi-Uniformities
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 575-583
-
- Article
-
- You have access
- Export citation
The Primality of N=2A3n-1
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 585-589
-
- Article
-
- You have access
- Export citation
Mathematical Notes
On the Local Connectedness of βX-X
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 591-594
-
- Article
-
- You have access
- Export citation
Research Article
Permutation Functions on a Finite Field
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 595-597
-
- Article
-
- You have access
- Export citation
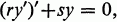
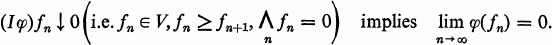
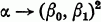
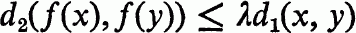
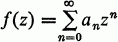
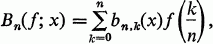
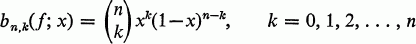
 is an algebra, L(
is an algebra, L( such that for each finite subset
such that for each finite subset