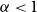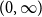1. Introduction
Consider a random simply generated tree. (For definitions of this and other concepts in the introduction, see Sections 2–3.) Under some technical conditions, amounting to the tree being equivalent to a critical conditioned Galton–Watson tree with finite offspring variance, the (height) profile of the tree converges in distribution, as a random function in
![]() $C[0,\infty)$
. Moreover, the limiting random function can be identified with the local time of a standard Brownian excursion; this was conjectured by Aldous [Reference Aldous3] and proved by Drmota and Gittenberger [Reference Drmota and Gittenberger18] (under a stronger assumption), see also Drmota [Reference Drmota17, Section 4.2], and in general by Kersting [Reference Kersting34] in a paper that unfortunately remains unpublished. See further Pitman [Reference Pitman47] for related results and a proof in a special case. See also Kersting [Reference Kersting34] for extensions when the offspring variance is infinite, a case not considered in the present paper.
$C[0,\infty)$
. Moreover, the limiting random function can be identified with the local time of a standard Brownian excursion; this was conjectured by Aldous [Reference Aldous3] and proved by Drmota and Gittenberger [Reference Drmota and Gittenberger18] (under a stronger assumption), see also Drmota [Reference Drmota17, Section 4.2], and in general by Kersting [Reference Kersting34] in a paper that unfortunately remains unpublished. See further Pitman [Reference Pitman47] for related results and a proof in a special case. See also Kersting [Reference Kersting34] for extensions when the offspring variance is infinite, a case not considered in the present paper.
Remark 1.1. To be precise, [Reference Drmota17] and [Reference Drmota and Gittenberger18] assume that the offspring distribution for the conditioned Galton–Watson tree has a finite exponential moment. As said in [Reference Drmota17, footnote on page 127], the analysis can be extended, but it seems that the proof of tightness in [Reference Drmota17], which is based on estimating fourth moments, requires a finite fourth moment of the offspring distribution.
Note also that Drmota [Reference Drmota17, ‘a shortcut’ pp. 123–125] besides the proof from [Reference Drmota and Gittenberger18] also gives an alternative proof that combines tightness (taken from the first proof) and the convergence of the contour process to a Brownian excursion shown by Aldous [Reference Aldous4], and thus avoids some intricate calculations in the first proof. We will use this method of proof below.
Using notation introduced below, the result can be stated as follows.
Theorem 1.2. (Drmota and Gittenberger [Reference Drmota and Gittenberger18], Kersting [Reference Kersting34]). Let
![]() $L_n$
be the (height) profile of a conditioned Galton–Watson tree of order n, with an offspring distribution that has mean 1 and finite variance
$L_n$
be the (height) profile of a conditioned Galton–Watson tree of order n, with an offspring distribution that has mean 1 and finite variance
![]() $\sigma^2$
. Then, as
$\sigma^2$
. Then, as
![]() ${{n\to\infty}}$
,
${{n\to\infty}}$
,
in the space
![]() $C[0,\infty]$
, where
$C[0,\infty]$
, where
![]() $L_\textbf{e}$
is a random function that can be identified with the local time of a standard Brownian excursion
$L_\textbf{e}$
is a random function that can be identified with the local time of a standard Brownian excursion
![]() $\textbf{e}$
; this means that for every bounded measurable
$\textbf{e}$
; this means that for every bounded measurable
![]() $f\,:\,[0,\infty)\to\mathbb R$
,
$f\,:\,[0,\infty)\to\mathbb R$
,
Remark 1.3. This result is often stated with convergence (1) in the space
![]() $C[0,\infty)$
; the version stated here with
$C[0,\infty)$
; the version stated here with
![]() $C[0,\infty]$
is somewhat stronger but follows easily. (Note that the maximum is a continuous functional on
$C[0,\infty]$
is somewhat stronger but follows easily. (Note that the maximum is a continuous functional on
![]() $C[0,\infty]$
but not on
$C[0,\infty]$
but not on
![]() $C[0,\infty)$
.) See further Section 2.4.
$C[0,\infty)$
.) See further Section 2.4.
The profile discussed above is the profile of the distances from the vertices to the root. Consider now instead the distance profile, defined as the profile of all distances between pairs of points. (Again, see Section 2 for details.) One of our main results is the following analogue of Theorem 1.2.
Theorem 1.4. Let
![]() $\Lambda_n$
be the distance profile of a conditioned Galton–Watson tree of order n, with an offspring distribution that has mean 1 and finite variance
$\Lambda_n$
be the distance profile of a conditioned Galton–Watson tree of order n, with an offspring distribution that has mean 1 and finite variance
![]() $\sigma^2>0$
. Then, as
$\sigma^2>0$
. Then, as
![]() ${{n\to\infty}}$
,
${{n\to\infty}}$
,
in the space
![]() $C[0,\infty]$
, where
$C[0,\infty]$
, where
![]() $\Lambda_{{\textbf{e}}}(x)$
is a continuous random function that can be described as the density of distances between random points in the Brownian continuum random tree [Reference Aldous2–Reference Aldous4]; equivalently, for a standard Brownian excursion
$\Lambda_{{\textbf{e}}}(x)$
is a continuous random function that can be described as the density of distances between random points in the Brownian continuum random tree [Reference Aldous2–Reference Aldous4]; equivalently, for a standard Brownian excursion
![]() $\textbf{e}$
, we have for every bounded measurable
$\textbf{e}$
, we have for every bounded measurable
![]() $f\,:\,[0,\infty)\to\mathbb R$
,
$f\,:\,[0,\infty)\to\mathbb R$
,
The random distance profile
![]() $\Lambda_n$
was earlier studied in [Reference Devroye and Janson16], where the estimate (123) below was shown.
$\Lambda_n$
was earlier studied in [Reference Devroye and Janson16], where the estimate (123) below was shown.
Remark 1.5. It is easy to see that the random function
![]() $\Lambda_\textbf{e}$
really is random and not deterministic, e.g. as a consequence of Theorem 13.1. However, we do not know its distribution, although the expectation
$\Lambda_\textbf{e}$
really is random and not deterministic, e.g. as a consequence of Theorem 13.1. However, we do not know its distribution, although the expectation
![]() ${\mathbb E{}}\Lambda_\textbf{e}(x)$
is given in Lemma 15.11. In particular, the following problem is open. (See [Reference Drmota17, Section 4.2.1] for such results, in several different forms, for
${\mathbb E{}}\Lambda_\textbf{e}(x)$
is given in Lemma 15.11. In particular, the following problem is open. (See [Reference Drmota17, Section 4.2.1] for such results, in several different forms, for
![]() $L_\textbf{e}$
.)
$L_\textbf{e}$
.)
Problem 1.6. Find a description of the (one-dimensional) distribution of
![]() $\Lambda_\textbf{e}(x)$
for fixed
$\Lambda_\textbf{e}(x)$
for fixed
![]() $x>0$
.
$x>0$
.
We have so far discussed rooted trees. However, the distance profile is defined also for unrooted trees, and we will find it convenient to use unrooted trees in parts of the proof. This leads us to consider random unrooted simply generated trees.
Simply generated families of rooted trees were introduced by Meir and Moon [Reference Meir and Moon42], leading to the notion of simply generated random rooted trees, see e.g. Drmota [Reference Drmota17]. This class of random rooted trees is one of the most popular classes of random trees, and these trees have been frequently studied in many different contexts by many authors. Simply generated random unrooted trees have been much less studied, but they have occurred, e.g. in a work on non-crossing trees by Kortchemski and Marzouk [Reference Kortchemski and Marzouk38] (see also Marckert and Panholzer [Reference Marckert and Panholzer41]). Nevertheless, we have not found a general treatment of them, so a minor purpose of the present paper is to do this in some detail, both for use in the paper and for future reference. We thus include (Sections 5–8) a general discussion of random unrooted simply generated trees, with some simple results relating them to rooted simply generated trees, allowing the transfer of many results for rooted simply generated trees to the unrooted case. Moreover, as part of the proof of Theorem 1.4, we prove the corresponding result (Theorem 11.2) for random unrooted simply generated trees.
As a preparation for the unrooted case, we also give (Section 4) some results (partly from Kortchemski and Marzouk [Reference Kortchemski and Marzouk38]) on modified rooted simply generated trees (Galton–Watson trees), where the root has different weights (offspring distribution) than all other vertices.
The central parts of the proof of Theorem 1.4 are given in Sections 10–12, where we use both rooted and unrooted trees. As a preparation, in Section 9, we extend Theorem 1.2 to conditioned modified Galton–Watson trees. We later also extend Theorem 1.4 to conditioned modified Galton–Watson trees (Theorem 12.1).
We end the paper with some comments and further results related to our main results. In Section 13, we discuss a simple application to the Wiener index of unrooted simply generated trees. Section 14 contains some important moment estimations of the distance profile for conditioned Galton–Watson trees as well as for its continuous counterpart
![]() $\Lambda_\textbf{e}$
. In Section 15, we establish Hölder continuity properties of the continuous random function
$\Lambda_\textbf{e}$
. In Section 15, we establish Hölder continuity properties of the continuous random function
![]() $L_\textbf{e}$
and
$L_\textbf{e}$
and
![]() $\Lambda_\textbf{e}$
. It is known that
$\Lambda_\textbf{e}$
. It is known that
![]() $L_\textbf{e}$
is a.s. Hölder continuous of order
$L_\textbf{e}$
is a.s. Hölder continuous of order
![]() $\alpha$
(abbreviated to Hölder(
$\alpha$
(abbreviated to Hölder(
![]() $\alpha$
)) for
$\alpha$
)) for
![]() $\alpha<\frac12$
, but not for
$\alpha<\frac12$
, but not for
![]() $\alpha\geqslant\frac12$
. We show that
$\alpha\geqslant\frac12$
. We show that
![]() $\Lambda_\textbf{e}$
is smoother; it is a.s. Hölder(
$\Lambda_\textbf{e}$
is smoother; it is a.s. Hölder(
![]() $\alpha$
) for
$\alpha$
) for
![]() $\alpha<1$
, and it is a.e. differentiable (Theorem 15.5). We do not know whether it is Lipschitz, or even continuously differentiable on
$\alpha<1$
, and it is a.e. differentiable (Theorem 15.5). We do not know whether it is Lipschitz, or even continuously differentiable on
![]() $[0,\infty)$
, but we show that it is does not a.s. have a two-sided derivative at 0 (Theorem 15.10), and we state some open problems.
$[0,\infty)$
, but we show that it is does not a.s. have a two-sided derivative at 0 (Theorem 15.10), and we state some open problems.
Finally, some further remarks are given in Section 16.
2. Some notation
Trees are finite except when explicitly said to be infinite. Trees may be rooted or unrooted; in a rooted tree, the root is denoted o. The rooted trees may be ordered or not. The unrooted trees will always be labelled; we do not consider unrooted unlabelled trees in the present paper.
If T is a tree, then its number of vertices is denoted by
![]() $|T|$
; this is called the order or the size of T. (Unlike some authors, we do not distinguish between order and size.) The notation
$|T|$
; this is called the order or the size of T. (Unlike some authors, we do not distinguish between order and size.) The notation
![]() $v\in T$
means that v is a vertex in T.
$v\in T$
means that v is a vertex in T.
The degree of a vertex
![]() $v\in T$
is denoted d(v). In a rooted tree, we also define the outdegree
$v\in T$
is denoted d(v). In a rooted tree, we also define the outdegree
![]() $d^+(v)$
as the number of children of v; thus,
$d^+(v)$
as the number of children of v; thus,
 \begin{align} d^+(v)= \begin{cases} d(v)-1, & v\neq o,\\d(v), & v=o. \end{cases}\end{align}
\begin{align} d^+(v)= \begin{cases} d(v)-1, & v\neq o,\\d(v), & v=o. \end{cases}\end{align}
A leaf in an unrooted tree is a vertex v with
![]() $d(v)=1$
. In a rooted tree, we instead require
$d(v)=1$
. In a rooted tree, we instead require
![]() $d^+(v)=0$
; this may make a difference only for the root.
$d^+(v)=0$
; this may make a difference only for the root.
A fringe subtree in a rooted tree is a subtree consisting of some vertex v and all its descendants. We regard v as the root of the fringe tree. The branches of a rooted tree are the fringe trees rooted at the children of the root. The number of branches thus equals the degree d(o) of the root.
Let
![]() $\mathfrak{T}_n$
be the set of all ordered rooted trees of order n, and let
$\mathfrak{T}_n$
be the set of all ordered rooted trees of order n, and let
![]() $\mathfrak{T}\,:\!=\,\bigcup_1^\infty\mathfrak{T}_n$
. Note that
$\mathfrak{T}\,:\!=\,\bigcup_1^\infty\mathfrak{T}_n$
. Note that
![]() $\mathfrak{T}_n$
is a finite set; we may identify the vertices of an ordered rooted tree by finite strings of positive integers, such that the root is the empty string and the children of v are vi,
$\mathfrak{T}_n$
is a finite set; we may identify the vertices of an ordered rooted tree by finite strings of positive integers, such that the root is the empty string and the children of v are vi,
![]() $i=1,\dots,d(v)$
. (Thus, an ordered rooted tree is regarded as a subtree of the infinite Ulam–Harris tree.) In fact, it is well known that
$i=1,\dots,d(v)$
. (Thus, an ordered rooted tree is regarded as a subtree of the infinite Ulam–Harris tree.) In fact, it is well known that
![]() $|\mathfrak{T}_n|=\frac{1}{n}\binom{2n-2}{n-1}$
, the Catalan number
$|\mathfrak{T}_n|=\frac{1}{n}\binom{2n-2}{n-1}$
, the Catalan number
![]() $C_{n-1}$
.
$C_{n-1}$
.
Let
![]() $\mathfrak{L}_n$
be the set of all unrooted trees of order n, with the labels
$\mathfrak{L}_n$
be the set of all unrooted trees of order n, with the labels
![]() $1,\dots,n$
; thus
$1,\dots,n$
; thus
![]() $\mathfrak{L}_n$
is the set of all trees on
$\mathfrak{L}_n$
is the set of all trees on
![]() $[n]\,:\!=\,{\{{1,\dots,n}\}}$
.
$[n]\,:\!=\,{\{{1,\dots,n}\}}$
.
![]() $\mathfrak{L}_n$
is evidently finite and by Cayley’s formula
$\mathfrak{L}_n$
is evidently finite and by Cayley’s formula
![]() $|\mathfrak{L}_n|=n^{n-2}$
. Let
$|\mathfrak{L}_n|=n^{n-2}$
. Let
![]() $\mathfrak{L}\,:\!=\,\bigcup_1^\infty\mathfrak{L}_n$
.
$\mathfrak{L}\,:\!=\,\bigcup_1^\infty\mathfrak{L}_n$
.
A probability sequence is the same as a probability distribution on
![]() $\mathbb N_0\,:\!=\,{\{{0,1,2,\dots}\}}$
, i.e., a sequence
$\mathbb N_0\,:\!=\,{\{{0,1,2,\dots}\}}$
, i.e., a sequence
![]() $\textbf{p}=(p_k)_0^\infty$
with
$\textbf{p}=(p_k)_0^\infty$
with
![]() $p_k\geqslant0$
and
$p_k\geqslant0$
and
![]() $\sum_{k=0}^\infty p_k=1$
. The mean
$\sum_{k=0}^\infty p_k=1$
. The mean
![]() $\mu(\textbf{p})$
and variance
$\mu(\textbf{p})$
and variance
![]() $\sigma^2(\textbf{p})$
of a probability sequence are defined to be the mean and variance of a random variable with distribution
$\sigma^2(\textbf{p})$
of a probability sequence are defined to be the mean and variance of a random variable with distribution
![]() $\textbf{p}$
, i.e.,
$\textbf{p}$
, i.e.,
 \begin{align} \mu(\textbf{p})\,:\!=\,\sum_{k=0}^\infty kp_k, &&&\sigma^2(\textbf{p})\,:\!=\,\sum_{k=0}^\infty k^2p_k-\mu(\textbf{p})^2.\end{align}
\begin{align} \mu(\textbf{p})\,:\!=\,\sum_{k=0}^\infty kp_k, &&&\sigma^2(\textbf{p})\,:\!=\,\sum_{k=0}^\infty k^2p_k-\mu(\textbf{p})^2.\end{align}
We use
![]() $\overset{\textrm{d}}{\longrightarrow}$
and
$\overset{\textrm{d}}{\longrightarrow}$
and
![]() $\overset{\textrm{p}}{\longrightarrow}$
for convergence in distribution and in probability, respectively, for a sequence of random variables in some metric space; see e.g. [Reference Billingsley11]. Also,
$\overset{\textrm{p}}{\longrightarrow}$
for convergence in distribution and in probability, respectively, for a sequence of random variables in some metric space; see e.g. [Reference Billingsley11]. Also,
![]() $\overset{\textrm{d}}{=}$
means convergence in distribution.
$\overset{\textrm{d}}{=}$
means convergence in distribution.
The total variation distance between two random variables X and Y in a metric space (or rather between their distributions) is defined by
taking the supremum over all measurable subsets A. It is well known that in a complete separable metric space, there exists a coupling of X and Y (i.e., a joint distribution with the given marginal distributions) such that
and this is best possible.
![]() $O_{\textrm{p}}(1)$
denotes a sequence of real-valued random variables
$O_{\textrm{p}}(1)$
denotes a sequence of real-valued random variables
![]() $(X_n)_n$
that is stochastically bounded, i.e., for every
$(X_n)_n$
that is stochastically bounded, i.e., for every
![]() $\varepsilon>0$
, there exists C such that
$\varepsilon>0$
, there exists C such that
![]() ${\mathbb P{}}(|X_n|>C)\leqslant\varepsilon$
. This is equivalent to
${\mathbb P{}}(|X_n|>C)\leqslant\varepsilon$
. This is equivalent to
![]() $(X_n)_n$
being tight. For tightness in more general metric spaces, see e.g. [Reference Billingsley11].
$(X_n)_n$
being tight. For tightness in more general metric spaces, see e.g. [Reference Billingsley11].
Let f be a real-valued function defined on an interval
![]() $I\subseteq\mathbb R$
. The modulus of continuity of f is the function
$I\subseteq\mathbb R$
. The modulus of continuity of f is the function
![]() $[0,\infty)\to[0,\infty]$
defined by, for
$[0,\infty)\to[0,\infty]$
defined by, for
![]() $\delta\geqslant0$
,
$\delta\geqslant0$
,
If x and y are real numbers,
![]() $x\land y\,:\!=\,\min{\{{x,y}\}}$
and
$x\land y\,:\!=\,\min{\{{x,y}\}}$
and
![]() $x\lor y\,:\!=\,\max{\{{x,y}\}}$
.
$x\lor y\,:\!=\,\max{\{{x,y}\}}$
.
C denotes unspecified constants that may vary from one occurrence to the next. They may depend on parameters such as weight sequences or offspring distributions, but they never depend on the size of the trees. Sometimes we write, e.g.,
![]() $C_r$
to emphasize that the constant depends on the parameter r.
$C_r$
to emphasize that the constant depends on the parameter r.
Unspecified limits are as
![]() ${{n\to\infty}}$
.
${{n\to\infty}}$
.
2.1. Profiles
For two vertices v and w in a tree T, let
![]() $\textsf{d}(x,y)=\textsf{d}_T(x,y)$
denote the distance between v and w, i.e., the number of edges in the unique path joining v and w. In particular, in a rooted tree,
$\textsf{d}(x,y)=\textsf{d}_T(x,y)$
denote the distance between v and w, i.e., the number of edges in the unique path joining v and w. In particular, in a rooted tree,
![]() $\textsf{d}(v,o)$
is the distance to the root, often called the depth (or sometimes height) of v.Footnote 1
$\textsf{d}(v,o)$
is the distance to the root, often called the depth (or sometimes height) of v.Footnote 1
For a rooted tree T, the height of T is
![]() $H(T)\,:\!=\,\max_{v\in T}\textsf{d}(v,o)$
, i.e., the maximum depth. The diameter of a tree T, rooted or not, is
$H(T)\,:\!=\,\max_{v\in T}\textsf{d}(v,o)$
, i.e., the maximum depth. The diameter of a tree T, rooted or not, is
![]() $\textrm{diam}(T)\,:\!=\,\max_{v,w\in T}\textsf{d}(v,w)$
.
$\textrm{diam}(T)\,:\!=\,\max_{v,w\in T}\textsf{d}(v,w)$
.
The profile of a rooted tree is the function
![]() $L=L_T\,:\,\mathbb R\to[0,\infty)$
defined by
$L=L_T\,:\,\mathbb R\to[0,\infty)$
defined by
for integers i, extended by linear interpolation to all real x. (We are mainly interested in
![]() $x\geqslant0$
, and trivially
$x\geqslant0$
, and trivially
![]() $L(x)=0$
for
$L(x)=0$
for
![]() $x\leqslant -1$
, but it will be convenient to allow negative x.) The linear interpolation can be written as
$x\leqslant -1$
, but it will be convenient to allow negative x.) The linear interpolation can be written as
where
![]() $\tau$
is the triangular function
$\tau$
is the triangular function
![]() $\tau(x)\,:\!=\,(1-|x|)\lor0$
.
$\tau(x)\,:\!=\,(1-|x|)\lor0$
.
Note that
![]() $L(0)=1$
, and that L is a continuous function with compact support
$L(0)=1$
, and that L is a continuous function with compact support
![]() $[\!-1,H(T)+1]$
. Furthermore, since
$[\!-1,H(T)+1]$
. Furthermore, since
![]() $\int\tau(x)\,\textrm{d} x=1$
,
$\int\tau(x)\,\textrm{d} x=1$
,
where we integrate from
![]() $-1$
because of the linear interpolation; we have
$-1$
because of the linear interpolation; we have
![]() $ \int_0^\infty L(x)\,\textrm{d} x = \sum_{i=0}^\infty L(i) -\frac12 = |T|-\frac12$
.
$ \int_0^\infty L(x)\,\textrm{d} x = \sum_{i=0}^\infty L(i) -\frac12 = |T|-\frac12$
.
The width of T is defined as
Similarly, in any tree T, rooted or unrooted, we define the distance profile as the function
![]() $\Lambda=\Lambda_T\,:\,[0,\infty)\to[0,\infty)$
defined by
$\Lambda=\Lambda_T\,:\,[0,\infty)\to[0,\infty)$
defined by
for integers i, again extended by linear interpolaton to all real
![]() $x\geqslant0$
. For definiteness, we count ordered pairs in (14), and we include the case
$x\geqslant0$
. For definiteness, we count ordered pairs in (14), and we include the case
![]() $v=w$
, so
$v=w$
, so
![]() $\Lambda(0)=|T|$
.
$\Lambda(0)=|T|$
.
![]() $\Lambda$
is a continuous function on
$\Lambda$
is a continuous function on
![]() $[0,\infty)$
with support
$[0,\infty)$
with support
![]() $[\!-1,\textrm{diam}(T)+1]$
. We have, similarly to (12),
$[\!-1,\textrm{diam}(T)+1]$
. We have, similarly to (12),
If T is an unrooted tree, let T(v) denote the rooted tree obtained by declaring v as the root, for
![]() $v\in T$
. Then, as a consequence of (10) and (14),
$v\in T$
. Then, as a consequence of (10) and (14),
Hence, the distance profile can be regarded as the sum (or, after normalisation, average) of the profiles for all possible choices of a root.
Remark 2.1. Alternatively, one might extend L to a step function by
![]() $L(x)\,:\!=\,L(\lfloor x\rfloor)$
, and similarly for
$L(x)\,:\!=\,L(\lfloor x\rfloor)$
, and similarly for
![]() $\Lambda$
. The asymptotic results are the same (and equivalent by simple arguments), with L and
$\Lambda$
. The asymptotic results are the same (and equivalent by simple arguments), with L and
![]() $\Lambda$
elements of
$\Lambda$
elements of
![]() $D[0,\infty]$
instead of
$D[0,\infty]$
instead of
![]() $C[0,\infty]$
and limit theorems taking place in that space. This has some advantages, but for technical reasons (e.g. simpler tightness criteria), we prefer to work in the space
$C[0,\infty]$
and limit theorems taking place in that space. This has some advantages, but for technical reasons (e.g. simpler tightness criteria), we prefer to work in the space
![]() $C[0,\infty]$
of continuous functions.
$C[0,\infty]$
of continuous functions.
Remark 2.2. Another version of
![]() $\Lambda$
would count unordered pairs of distinct vertices. The two versions are obviously equivalent and our results hold for the alternative version too, mutatis mutandis.
$\Lambda$
would count unordered pairs of distinct vertices. The two versions are obviously equivalent and our results hold for the alternative version too, mutatis mutandis.
2.2. Brownian excursion and its local time
The standard Brownian excursion
![]() $\textbf{e}$
is a random continuous function
$\textbf{e}$
is a random continuous function
![]() ${[0,1]}\to[0,\infty)$
such that
${[0,1]}\to[0,\infty)$
such that
![]() $\textbf{e}(0)=\textbf{e}(1)=0$
and
$\textbf{e}(0)=\textbf{e}(1)=0$
and
![]() $\textbf{e}(t)>0$
for
$\textbf{e}(t)>0$
for
![]() $t\in(0,1)$
. Informally,
$t\in(0,1)$
. Informally,
![]() $\textbf{e}$
can be regarded as a Brownian motion conditioned on these properties; this can be formalised as an appropriate limit [Reference Durrett, Iglehart and Miller23]. There are several other, quite different but equivalent, definitions, see e.g. [Reference Revuz and Yor49, XII.(2.13)], [Reference Blumenthal13, Example II.1d)], and [Reference Drmota17, Section 4.1.3].
$\textbf{e}$
can be regarded as a Brownian motion conditioned on these properties; this can be formalised as an appropriate limit [Reference Durrett, Iglehart and Miller23]. There are several other, quite different but equivalent, definitions, see e.g. [Reference Revuz and Yor49, XII.(2.13)], [Reference Blumenthal13, Example II.1d)], and [Reference Drmota17, Section 4.1.3].
The local time
![]() $L_\textbf{e}$
of
$L_\textbf{e}$
of
![]() $\textbf{e}$
is a continuous random function that is defined (almost surely) as a functional of
$\textbf{e}$
is a continuous random function that is defined (almost surely) as a functional of
![]() $\textbf{e}$
satisfying
$\textbf{e}$
satisfying
for every bounded (or non-negative) measurable function
![]() $f\,:\,[0,\infty)\to\mathbb R$
. In particular, (17) yields, for any
$f\,:\,[0,\infty)\to\mathbb R$
. In particular, (17) yields, for any
![]() $x\geqslant0$
and
$x\geqslant0$
and
![]() $\varepsilon>0$
,
$\varepsilon>0$
,
and thus
Hence,
![]() $L_\textbf{e}(x)$
can be regarded as the occupation density of
$L_\textbf{e}(x)$
can be regarded as the occupation density of
![]() $\textbf{e}$
at the value x.
$\textbf{e}$
at the value x.
Note that the existence (almost surely) of a function
![]() $L_\textbf{e}(x)$
satisfying (17)–(19) is far from obvious; this is part of the general theory of local times for semimartingales, see e.g. [Reference Revuz and Yor49, Chapter VI]. The existence also follows from (some of) the proofs of Theorem 1.2.
$L_\textbf{e}(x)$
satisfying (17)–(19) is far from obvious; this is part of the general theory of local times for semimartingales, see e.g. [Reference Revuz and Yor49, Chapter VI]. The existence also follows from (some of) the proofs of Theorem 1.2.
2.3. Brownian continuum random tree
Given a continuous function
![]() $g\,:\,{[0,1]}\to[0,\infty)$
with
$g\,:\,{[0,1]}\to[0,\infty)$
with
![]() $g(0)=g(1)=0$
, one can define a pseudometric
$g(0)=g(1)=0$
, one can define a pseudometric
![]() $\textsf{d}$
on
$\textsf{d}$
on
![]() ${[0,1]}$
by
${[0,1]}$
by
By identifying points with distance 0, we obtain a metric space
![]() $T_g$
, which is a compact real tree, see e.g. Le Gall [Reference Le Gall39, Theorem 2.2]. We denote the natural quotient map
$T_g$
, which is a compact real tree, see e.g. Le Gall [Reference Le Gall39, Theorem 2.2]. We denote the natural quotient map
![]() ${[0,1]}\to T_g$
by
${[0,1]}\to T_g$
by
![]() $\rho_g$
, and let
$\rho_g$
, and let
![]() $T_g$
be rooted at
$T_g$
be rooted at
![]() $\rho_{g}(0)$
. The Brownian continuum random tree defined by Aldous[Reference Aldous2–Reference Aldous4] can be defined as the random real tree
$\rho_{g}(0)$
. The Brownian continuum random tree defined by Aldous[Reference Aldous2–Reference Aldous4] can be defined as the random real tree
![]() $T_{\textbf{e}}$
constructed in this way from the random Brownian excursion
$T_{\textbf{e}}$
constructed in this way from the random Brownian excursion
![]() $\textbf{e}$
, see [Reference Le Gall39, Section 2.3]. (Aldous [Reference Aldous2–Reference Aldous4] used another definition, and another scaling corresponding to
$\textbf{e}$
, see [Reference Le Gall39, Section 2.3]. (Aldous [Reference Aldous2–Reference Aldous4] used another definition, and another scaling corresponding to
![]() $T_{2\textbf{e}}$
.) Note that using (20), (4) can be written
$T_{2\textbf{e}}$
.) Note that using (20), (4) can be written
for any bounded (or non-negative) measurable function f. This means that
![]() $\Lambda_\textbf{e}$
is the density of the distance in
$\Lambda_\textbf{e}$
is the density of the distance in
![]() $T_\textbf{e}$
between two random points, chosen independently with the probability measure on
$T_\textbf{e}$
between two random points, chosen independently with the probability measure on
![]() $T_\textbf{e}$
induced by the uniform measure on
$T_\textbf{e}$
induced by the uniform measure on
![]() ${[0,1]}$
. This justifies the equivalence of the two definitions of
${[0,1]}$
. This justifies the equivalence of the two definitions of
![]() $\Lambda_\textbf{e}$
stated in Theorem 1.4. As for the local time
$\Lambda_\textbf{e}$
stated in Theorem 1.4. As for the local time
![]() $L_\textbf{e}$
, the existence (almost surely) of a continuous function
$L_\textbf{e}$
, the existence (almost surely) of a continuous function
![]() $\Lambda_\textbf{e}$
satisfying (21) is far from trivial; this will be a consequence of our proof.
$\Lambda_\textbf{e}$
satisfying (21) is far from trivial; this will be a consequence of our proof.
An important feature of the Brownian continuum random tree is its re-rooting invariance property. More precisely, fix
![]() $s \in [0,1]$
and set
$s \in [0,1]$
and set
 \begin{align} \textbf{e}^{[s]}(t)= \begin{cases}\textsf{d}(s,s+t;\,\textbf{e}), & 0\leqslant t < 1-s\\\textsf{d}(s,s+t-1;\,\textbf{e}), &1-s \leqslant t \leqslant 1. \end{cases}\end{align}
\begin{align} \textbf{e}^{[s]}(t)= \begin{cases}\textsf{d}(s,s+t;\,\textbf{e}), & 0\leqslant t < 1-s\\\textsf{d}(s,s+t-1;\,\textbf{e}), &1-s \leqslant t \leqslant 1. \end{cases}\end{align}
Note that
![]() $\textbf{e}^{[s]}$
is a random continuous function
$\textbf{e}^{[s]}$
is a random continuous function
![]() ${[0,1]}\to[0,\infty)$
such that
${[0,1]}\to[0,\infty)$
such that
![]() $\textbf{e}^{[s]}(0)=\textbf{e}^{[s]}(1)=0$
and a.s.
$\textbf{e}^{[s]}(0)=\textbf{e}^{[s]}(1)=0$
and a.s.
![]() $\textbf{e}^{[s]}(t)>0$
for
$\textbf{e}^{[s]}(t)>0$
for
![]() $t\in(0,1)$
; clearly,
$t\in(0,1)$
; clearly,
![]() $\textbf{e}^{[0]} = \textbf{e}$
. By Duquesne and Le Gall [Reference Duquesne and Le Gall21, Lemma 2.2], the compact real tree
$\textbf{e}^{[0]} = \textbf{e}$
. By Duquesne and Le Gall [Reference Duquesne and Le Gall21, Lemma 2.2], the compact real tree
![]() $T_{\textbf{e}^{[s]}}$
is then canonically identified with the
$T_{\textbf{e}^{[s]}}$
is then canonically identified with the
![]() $T_{\textbf{e}}$
tree re-rooted at the vertex
$T_{\textbf{e}}$
tree re-rooted at the vertex
![]() $\rho_{\textbf{e}}(s)$
. Marckert and Mokkadem [Reference Marckert and Mokkadem40, Proposition 4.9] (see also Duquesne and Le Gall [Reference Duquesne and Le Gall22, Theorem 2.2]) have shown that for every fixed
$\rho_{\textbf{e}}(s)$
. Marckert and Mokkadem [Reference Marckert and Mokkadem40, Proposition 4.9] (see also Duquesne and Le Gall [Reference Duquesne and Le Gall22, Theorem 2.2]) have shown that for every fixed
![]() $s \in [0,1]$
,
$s \in [0,1]$
,
in distribution. Thus, the re-rooted tree
![]() $T_{\textbf{e}^{[s]}}$
is a version of the Brownian continuum random tree.
$T_{\textbf{e}^{[s]}}$
is a version of the Brownian continuum random tree.
Remark 2.3. Indeed, Aldous [Reference Aldous3, (20)] already observed that the Brownian continuum random tree is invariant under uniform re-rooting and that this property corresponds to the invariance of the law of the Brownian excursion under the path transformation (22) if
![]() $s = U$
is uniformly random on [0, 1] and independent of
$s = U$
is uniformly random on [0, 1] and independent of
![]() $\textbf{e}$
.
$\textbf{e}$
.
As a consequence of the previous re-rooting invariance property, we deduce the following explicit expression for the continuous function
![]() $\Lambda_\textbf{e}$
. For every fixed
$\Lambda_\textbf{e}$
. For every fixed
![]() $s \in [0,1]$
, let
$s \in [0,1]$
, let
![]() $L_{\textbf{e}^{[s]}}$
denote the local time of
$L_{\textbf{e}^{[s]}}$
denote the local time of
![]() $\textbf{e}^{[s]}$
, which is perfectly defined thanks to (23). It follows from (20), (21) and (22) that
$\textbf{e}^{[s]}$
, which is perfectly defined thanks to (23). It follows from (20), (21) and (22) that
for any bounded (or non-negative) measurable function f, or equivalently,
In accordance with the discrete analogue of
![]() $\Lambda_\textbf{e}$
in (16), the identity (24) shows that
$\Lambda_\textbf{e}$
in (16), the identity (24) shows that
![]() $\Lambda_\textbf{e}$
can be regarded as the average of the profiles for all possible choices of a root in
$\Lambda_\textbf{e}$
can be regarded as the average of the profiles for all possible choices of a root in
![]() $T_{\textbf{e}}$
.
$T_{\textbf{e}}$
.
2.4. The function spaces
 $C[0,\infty)$
and
$C[0,\infty)$
and
 $C[0,\infty]$
$C[0,\infty]$
Recall that
![]() $C[0,\infty)$
is the space of continuous functions on
$C[0,\infty)$
is the space of continuous functions on
![]() $[0,\infty)$
and that convergence in
$[0,\infty)$
and that convergence in
![]() $C[0,\infty)$
means uniform convergence on each compact interval [0, b]. As said in Remark 1.3, we prefer to state our results in the space
$C[0,\infty)$
means uniform convergence on each compact interval [0, b]. As said in Remark 1.3, we prefer to state our results in the space
![]() $C[0,\infty]$
of functions that are continuous on the extended half-line
$C[0,\infty]$
of functions that are continuous on the extended half-line
![]() $[0,\infty]$
. These are the functions f in
$[0,\infty]$
. These are the functions f in
![]() $C[0,\infty)$
such that the limit
$C[0,\infty)$
such that the limit
![]() $f(\infty)\,:\!=\,\lim_{{{x\to\infty}}}f(x)$
exists; in our case, this is a triviality since all random functions on both sides of (1) and (3), and in similar later statements, have compact support, and thus trivially extend continuously to
$f(\infty)\,:\!=\,\lim_{{{x\to\infty}}}f(x)$
exists; in our case, this is a triviality since all random functions on both sides of (1) and (3), and in similar later statements, have compact support, and thus trivially extend continuously to
![]() $[0,\infty]$
with
$[0,\infty]$
with
![]() $f(\infty)=0$
. The important difference between
$f(\infty)=0$
. The important difference between
![]() $C[0,\infty)$
and
$C[0,\infty)$
and
![]() $C[0,\infty]$
is instead the topology: convergence in
$C[0,\infty]$
is instead the topology: convergence in
![]() $C[0,\infty]$
means uniform convergence on
$C[0,\infty]$
means uniform convergence on
![]() $[0,\infty]$
(or, equivalently, on
$[0,\infty]$
(or, equivalently, on
![]() $[0,\infty)$
).
$[0,\infty)$
).
In particular, the supremum is a continuous functional on
![]() $C[0,\infty]$
, but not on
$C[0,\infty]$
, but not on
![]() $C[0,\infty)$
(where it also may be infinite). Thus, convergence of the width (after rescaling), follows immediately from Theorem 1.2 (see also the proof of Theorem 9.2); if this was stated with convergence in
$C[0,\infty)$
(where it also may be infinite). Thus, convergence of the width (after rescaling), follows immediately from Theorem 1.2 (see also the proof of Theorem 9.2); if this was stated with convergence in
![]() $C[0,\infty)$
, a small extra argument would be needed (more or less equivalent to showing convergence in
$C[0,\infty)$
, a small extra argument would be needed (more or less equivalent to showing convergence in
![]() $C[0,\infty]$
).
$C[0,\infty]$
).
In the random setting, the difference between the two topologies can be expressed as in the following lemma. See also [Reference Janson27, Proposition 2.4], for the similar case of the spaces
![]() $D[0,\infty]$
and
$D[0,\infty]$
and
![]() $D[0,\infty)$
.
$D[0,\infty)$
.
Lemma 2.4. Let
![]() $X_n(t)$
and X(t) be random functions in
$X_n(t)$
and X(t) be random functions in
![]() $C[0,\infty]$
. Then
$C[0,\infty]$
. Then
![]() $X_n(t)\overset{{d}}{\longrightarrow} X(t)$
in
$X_n(t)\overset{{d}}{\longrightarrow} X(t)$
in
![]() $C[0,\infty]$
if and only if
$C[0,\infty]$
if and only if
-
(i)
 $X_n(t)\overset{\textrm{d}}{\longrightarrow} X(t)$
in
$X_n(t)\overset{\textrm{d}}{\longrightarrow} X(t)$
in
 $C[0,\infty)$
, and
$C[0,\infty)$
, and -
(ii)
 $X_n(t)\overset{\textrm{p}}{\longrightarrow} X_n(\infty)$
, as
$X_n(t)\overset{\textrm{p}}{\longrightarrow} X_n(\infty)$
, as
 ${{t\to\infty}}$
, uniformly in n; i.e., for every
${{t\to\infty}}$
, uniformly in n; i.e., for every
 $\varepsilon>0$
, (25)
$\varepsilon>0$
, (25) \begin{align} \sup_{n\geqslant1}{\mathbb P{}}\bigl({\sup_{u<t<\infty}|X_n(t)-X_n(\infty)|>\varepsilon}\bigr)\to 0,\qquad \text{as }u\to\infty. \end{align}
\begin{align} \sup_{n\geqslant1}{\mathbb P{}}\bigl({\sup_{u<t<\infty}|X_n(t)-X_n(\infty)|>\varepsilon}\bigr)\to 0,\qquad \text{as }u\to\infty. \end{align}
Proof. A straightforward exercise.
In our cases, such as (1) and (3), the condition (25) is easily verified from convergence (or just tightness) of the normalised height
![]() $H_n/\sqrt n$
, which can be used to bound the support of the left-hand sides. Hence, convergence in
$H_n/\sqrt n$
, which can be used to bound the support of the left-hand sides. Hence, convergence in
![]() $C[0,\infty)$
and
$C[0,\infty)$
and
![]() $C[0,\infty]$
is essentially equivalent.
$C[0,\infty]$
is essentially equivalent.
Note that
![]() $C[0,\infty]$
is a separable Banach space, and that it is isomorphic to
$C[0,\infty]$
is a separable Banach space, and that it is isomorphic to
![]() $C{[0,1]}$
by a change of variable; thus, general results for
$C{[0,1]}$
by a change of variable; thus, general results for
![]() $C{[0,1]}$
may be transferred. Note also that all functions that we are interested in lie in the (Banach) subspace
$C{[0,1]}$
may be transferred. Note also that all functions that we are interested in lie in the (Banach) subspace
![]() $C_0[0,\infty)\,:\!=\,{\{{f\in C[0,\infty]\,:\,f(\infty)=0}\}}$
. Hence, the results may just as well be stated as convergence in distribution in
$C_0[0,\infty)\,:\!=\,{\{{f\in C[0,\infty]\,:\,f(\infty)=0}\}}$
. Hence, the results may just as well be stated as convergence in distribution in
![]() $C_0[0,\infty)$
.
$C_0[0,\infty)$
.
3. Rooted simply generated trees
As a background, we recall first the definition of random rooted simply generated trees and the almost equivalent conditioned Galton–Watson trees, see e.g. [Reference Drmota17] or [Reference Janson30] for further details, and [Reference Athreya and Ney6] for more on Galton–Watson processes.
3.1. Simply generated trees
Let
![]() $\boldsymbol{\phi}=(\phi_k)_0^\infty$
be a given sequence of non-negative weights, with
$\boldsymbol{\phi}=(\phi_k)_0^\infty$
be a given sequence of non-negative weights, with
![]() $\phi_0>0$
and
$\phi_0>0$
and
![]() $\phi_k>0$
for at least one
$\phi_k>0$
for at least one
![]() $k\geqslant2$
. (The latter conditions exclude only trivial cases when the random tree
$k\geqslant2$
. (The latter conditions exclude only trivial cases when the random tree
![]() ${\mathcal T}^{{\boldsymbol{\phi}}}_n$
defined below either does not exist or is a deterministic path.)
${\mathcal T}^{{\boldsymbol{\phi}}}_n$
defined below either does not exist or is a deterministic path.)
For any rooted ordered tree
![]() $T\in\mathfrak{T}$
, define the weight of T as
$T\in\mathfrak{T}$
, define the weight of T as
For a given n, we define the random rooted simply generated tree
![]() ${\mathcal T}^{{\boldsymbol{\phi}}}_n$
of order n as a random tree in
${\mathcal T}^{{\boldsymbol{\phi}}}_n$
of order n as a random tree in
![]() $\mathfrak{T}_n$
with probability proportional to its weight; i.e.,
$\mathfrak{T}_n$
with probability proportional to its weight; i.e.,
We consider only n such that at least one tree T with
![]() $\phi(T)>0$
exists.
$\phi(T)>0$
exists.
A weight sequence
![]() $\boldsymbol{\phi}'=(\phi^{\prime}_k)_0^\infty$
with
$\boldsymbol{\phi}'=(\phi^{\prime}_k)_0^\infty$
with
for some
![]() $a,b>0$
is said to be equivalent to
$a,b>0$
is said to be equivalent to
![]() $(\phi_k)_0^\infty$
. It is easily seen that equivalent weight sequences define the same random tree
$(\phi_k)_0^\infty$
. It is easily seen that equivalent weight sequences define the same random tree
![]() ${\mathcal T}^{{\boldsymbol{\phi}}}_n$
, i.e.,
${\mathcal T}^{{\boldsymbol{\phi}}}_n$
, i.e.,
![]() ${\mathcal T}^{{\boldsymbol{\phi}'}}_n\overset{\textrm{d}}{=}{\mathcal T}^{{\boldsymbol{\phi}}}_n$
.
${\mathcal T}^{{\boldsymbol{\phi}'}}_n\overset{\textrm{d}}{=}{\mathcal T}^{{\boldsymbol{\phi}}}_n$
.
3.2. Galton–Watson trees
Given a probability sequence
![]() $\textbf{p}=(p_k)_0^\infty$
, the Galton–Watson tree
$\textbf{p}=(p_k)_0^\infty$
, the Galton–Watson tree
![]() ${\mathcal T}^{{\textbf{p}}}$
is the family tree of a Galton–Watson process with offspring distribution
${\mathcal T}^{{\textbf{p}}}$
is the family tree of a Galton–Watson process with offspring distribution
![]() $\textbf{p}$
. This means that
$\textbf{p}$
. This means that
![]() ${\mathcal T}^{{\textbf{p}}}$
is a random ordered rooted tree, which is constructed as follows: Start with a root and give it a random number of children with the distribution
${\mathcal T}^{{\textbf{p}}}$
is a random ordered rooted tree, which is constructed as follows: Start with a root and give it a random number of children with the distribution
![]() $\textbf{p}$
. Give each new vertex a random number of children with the same distribution and independent of previous choices, and continue as long as there are new vertices. In general,
$\textbf{p}$
. Give each new vertex a random number of children with the same distribution and independent of previous choices, and continue as long as there are new vertices. In general,
![]() ${\mathcal T}^{{\textbf{p}}}$
may be an infinite tree. We will mainly consider the critical case when the expectation
${\mathcal T}^{{\textbf{p}}}$
may be an infinite tree. We will mainly consider the critical case when the expectation
![]() $\mu(\textbf{p})=1$
, and then it is well known that
$\mu(\textbf{p})=1$
, and then it is well known that
![]() ${\mathcal T}^{{\textbf{p}}}$
is finite a.s. (We exclude the trivial case when
${\mathcal T}^{{\textbf{p}}}$
is finite a.s. (We exclude the trivial case when
![]() $p_1=1$
.)
$p_1=1$
.)
The size
![]() $|{\mathcal T}^{{\textbf{p}}}|$
of a Galton–Watson tree is random. Given
$|{\mathcal T}^{{\textbf{p}}}|$
of a Galton–Watson tree is random. Given
![]() $n\geqslant1$
, the conditioned Galton–Watson tree
$n\geqslant1$
, the conditioned Galton–Watson tree
![]() ${\mathcal T}^{{\textbf{p}}}_n$
is defined as
${\mathcal T}^{{\textbf{p}}}_n$
is defined as
![]() ${\mathcal T}^{{\textbf{p}}}$
conditioned on
${\mathcal T}^{{\textbf{p}}}$
conditioned on
![]() $|{\mathcal T}^{{\textbf{p}}}|=n$
. (We consider only n such that this happens with positive probability.) Consequently,
$|{\mathcal T}^{{\textbf{p}}}|=n$
. (We consider only n such that this happens with positive probability.) Consequently,
![]() ${\mathcal T}^{{\textbf{p}}}_n$
is a random ordered rooted tree of size n. It is easily seen that a conditioned Galton–Watson tree
${\mathcal T}^{{\textbf{p}}}_n$
is a random ordered rooted tree of size n. It is easily seen that a conditioned Galton–Watson tree
![]() ${\mathcal T}^{{\textbf{p}}}_n$
equals (in distribution) the simply generated tree with the weight sequence
${\mathcal T}^{{\textbf{p}}}_n$
equals (in distribution) the simply generated tree with the weight sequence
![]() $\textbf{p}$
, and thus we use the same notation
$\textbf{p}$
, and thus we use the same notation
![]() ${\mathcal T}^{{\textbf{p}}}_n$
for both.
${\mathcal T}^{{\textbf{p}}}_n$
for both.
A (conditioned) Galton–Watson tree is critical if its offspring distribution
![]() $\textbf{p}$
has mean
$\textbf{p}$
has mean
![]() $\mu(\textbf{p})=1$
. We will in the present paper mainly consider conditioned Galton–Watson trees that are critical and have a finite variance
$\mu(\textbf{p})=1$
. We will in the present paper mainly consider conditioned Galton–Watson trees that are critical and have a finite variance
![]() $\sigma^2(\textbf{p})$
; this condition is rather mild, as is seen in the following subsection.
$\sigma^2(\textbf{p})$
; this condition is rather mild, as is seen in the following subsection.
3.3. Equivalence
A random simply generated tree
![]() ${\mathcal T}^{{\boldsymbol{\phi}}}_n$
with a weight sequence
${\mathcal T}^{{\boldsymbol{\phi}}}_n$
with a weight sequence
![]() $(\phi_k)_0^\infty$
that is a probability sequence equals, as just said, the conditioned Galton–Watson tree
$(\phi_k)_0^\infty$
that is a probability sequence equals, as just said, the conditioned Galton–Watson tree
![]() ${\mathcal T}^{{\boldsymbol{\phi}}}_n$
. Much more generally, any weight sequence
${\mathcal T}^{{\boldsymbol{\phi}}}_n$
. Much more generally, any weight sequence
![]() $\boldsymbol{\phi}$
such that its generating function
$\boldsymbol{\phi}$
such that its generating function
 \begin{align} \Phi(z)\,:\!=\,\sum_{k=0}^\infty \phi_k z^k\end{align}
\begin{align} \Phi(z)\,:\!=\,\sum_{k=0}^\infty \phi_k z^k\end{align}
has positive radius of convergence is equivalent to some probability weight sequence; hence,
![]() ${\mathcal T}^{{\boldsymbol{\phi}}}_n$
can be regarded as a conditioned Galton–Watson tree in this case too. Moreover, in many cases, we can choose an equivalent probability weight sequence that has mean 1 and finite variance; see e.g. [Reference Janson30, Section 4].
${\mathcal T}^{{\boldsymbol{\phi}}}_n$
can be regarded as a conditioned Galton–Watson tree in this case too. Moreover, in many cases, we can choose an equivalent probability weight sequence that has mean 1 and finite variance; see e.g. [Reference Janson30, Section 4].
We will use this to switch between simply generated trees and conditioned Galton–Watson trees without comment in the sequel; we will use the name that seems best and most natural in different contexts.
3.4. Simply generated forests
The Galton–Watson process above starts with one individual. More generally, we may start with m individuals, which we may assume are numbered
![]() $1,\dots,m$
; this yields a Galton–Watson forest consisting of m independent copies of
$1,\dots,m$
; this yields a Galton–Watson forest consisting of m independent copies of
![]() ${\mathcal T}^{{\textbf{p}}}$
. Conditioning on the total size being
${\mathcal T}^{{\textbf{p}}}$
. Conditioning on the total size being
![]() $n\geqslant m$
, we obtain a conditioned Galton–Watson forest
$n\geqslant m$
, we obtain a conditioned Galton–Watson forest
![]() ${\mathcal T}^{{\textbf{p}}}_{n,m}$
, which thus consists of m random trees
${\mathcal T}^{{\textbf{p}}}_{n,m}$
, which thus consists of m random trees
![]() ${\mathcal T}^{{\textbf{p}}}_{n,m;\,1}, \dots,{\mathcal T}^{{\textbf{p}}}_{n,m;\,m}$
with
${\mathcal T}^{{\textbf{p}}}_{n,m;\,1}, \dots,{\mathcal T}^{{\textbf{p}}}_{n,m;\,m}$
with
![]() $|{\mathcal T}^{{\textbf{p}}}_{n,m;\,1}|+\dots+|{\mathcal T}^{{\textbf{p}}}_{n,m;\,{m}}|=n$
. Conditioned on the sizes
$|{\mathcal T}^{{\textbf{p}}}_{n,m;\,1}|+\dots+|{\mathcal T}^{{\textbf{p}}}_{n,m;\,{m}}|=n$
. Conditioned on the sizes
![]() $|{\mathcal T}^{{\textbf{p}}}_{n,m;\,1}|,\dots,|{\mathcal T}^{{\textbf{p}}}_{n,m;\,m}|$
, the trees are independent conditioned Galton–Watson trees with the given sizes.
$|{\mathcal T}^{{\textbf{p}}}_{n,m;\,1}|,\dots,|{\mathcal T}^{{\textbf{p}}}_{n,m;\,m}|$
, the trees are independent conditioned Galton–Watson trees with the given sizes.
More generally, given any weight sequence
![]() $\boldsymbol{\phi}$
, a random simply generated forest
$\boldsymbol{\phi}$
, a random simply generated forest
![]() ${\mathcal T}^{{\boldsymbol{\phi}}}_{n,m}$
is a random forest with m rooted trees and total size n, chosen with probability proportional to its weight, defined as in (26). Again, conditioned on their sizes, the trees are independent simply generated trees.
${\mathcal T}^{{\boldsymbol{\phi}}}_{n,m}$
is a random forest with m rooted trees and total size n, chosen with probability proportional to its weight, defined as in (26). Again, conditioned on their sizes, the trees are independent simply generated trees.
Thus, the distribution of the sizes of the trees in the forest is of major importance. Consider the Galton–Watson case, and let
![]() ${\mathcal T}^{{\textbf{p}}}_{n,m;\,(1)}, \dots,{\mathcal T}^{{\textbf{p}}}_{n,m;\,(m)}$
denote the trees arranged in decreasing order:
${\mathcal T}^{{\textbf{p}}}_{n,m;\,(1)}, \dots,{\mathcal T}^{{\textbf{p}}}_{n,m;\,(m)}$
denote the trees arranged in decreasing order:
![]() $|{\mathcal T}^{{\textbf{p}}}_{n,m;\,(1)}|\geqslant\dots\geqslant|{\mathcal T}^{{\textbf{p}}}_{n,m;\,(m)}|$
. (Ties are resolved randomly, say; this applies tacitly to all similar situations.) We have the following general result, which was proved by Marzouk [38, Lemma 5.7(iii)] under an additional regularity hypothesis.
$|{\mathcal T}^{{\textbf{p}}}_{n,m;\,(1)}|\geqslant\dots\geqslant|{\mathcal T}^{{\textbf{p}}}_{n,m;\,(m)}|$
. (Ties are resolved randomly, say; this applies tacitly to all similar situations.) We have the following general result, which was proved by Marzouk [38, Lemma 5.7(iii)] under an additional regularity hypothesis.
Lemma 3.1. Let
![]() $m\geqslant1$
be fixed, and consider the conditioned Galton–Watson forest
$m\geqslant1$
be fixed, and consider the conditioned Galton–Watson forest
![]() ${\mathcal T}^{{{\textbf{p}}}}_{n,m}$
as
${\mathcal T}^{{{\textbf{p}}}}_{n,m}$
as
![]() ${{n\to\infty}}$
. Then
${{n\to\infty}}$
. Then
 \begin{align}|{\mathcal T}^{{{\textbf{p}}}}_{n,m;\,(i)}|= \begin{cases}n-O_{\textrm{p}}(1), & i=1\\O_{\textrm{p}}(1), & i=2,\dots,m. \end{cases}\end{align}
\begin{align}|{\mathcal T}^{{{\textbf{p}}}}_{n,m;\,(i)}|= \begin{cases}n-O_{\textrm{p}}(1), & i=1\\O_{\textrm{p}}(1), & i=2,\dots,m. \end{cases}\end{align}
Proof. Suppose first that
![]() $\mu(\textbf{p})=1$
. Suppose also, for simplicity, that
$\mu(\textbf{p})=1$
. Suppose also, for simplicity, that
![]() $p_m>0$
. Consider the conditioned Galton–Watson tree
$p_m>0$
. Consider the conditioned Galton–Watson tree
![]() ${\mathcal T}^{{\textbf{p}}}_{n+1}$
and condition on the event
${\mathcal T}^{{\textbf{p}}}_{n+1}$
and condition on the event
![]() $\mathcal E_m$
that the root degree is m. Conditioned on
$\mathcal E_m$
that the root degree is m. Conditioned on
![]() $\mathcal E_m$
, there are m branches, which form a conditioned Galton–Watson forest
$\mathcal E_m$
, there are m branches, which form a conditioned Galton–Watson forest
![]() ${\mathcal T}^{{\textbf{p}}}_{n,m}$
.
${\mathcal T}^{{\textbf{p}}}_{n,m}$
.
As
![]() ${{n\to\infty}}$
, the random tree
${{n\to\infty}}$
, the random tree
![]() ${\mathcal T}^{{\textbf{p}}}_{n+1}$
converges in distribution to an infinite random tree
${\mathcal T}^{{\textbf{p}}}_{n+1}$
converges in distribution to an infinite random tree
![]() $\widehat{{\mathcal T}}$
(the size-biased Galton–Watson tree defined by Kesten [Reference Kesten35]), see [Reference Janson30, Theorem 7.1]. Moreover,
$\widehat{{\mathcal T}}$
(the size-biased Galton–Watson tree defined by Kesten [Reference Kesten35]), see [Reference Janson30, Theorem 7.1]. Moreover,
![]() ${\mathbb P{}}(\mathcal E_m)\to mp_m>0$
by [Reference Janson30, Theorem 7.10]. Hence,
${\mathbb P{}}(\mathcal E_m)\to mp_m>0$
by [Reference Janson30, Theorem 7.10]. Hence,
![]() ${\mathcal T}^{{\textbf{p}}}_{n+1}$
conditioned on
${\mathcal T}^{{\textbf{p}}}_{n+1}$
conditioned on
![]() $\mathcal E_m$
converges in distribution to
$\mathcal E_m$
converges in distribution to
![]() $\widehat{{\mathcal T}}$
conditioned on
$\widehat{{\mathcal T}}$
conditioned on
![]() $\mathcal E_m$
. In other words, the forest
$\mathcal E_m$
. In other words, the forest
![]() ${\mathcal T}^{{\textbf{p}}}_{n,m}$
converges in distribution to the branches of
${\mathcal T}^{{\textbf{p}}}_{n,m}$
converges in distribution to the branches of
![]() $\widehat{{\mathcal T}}$
conditioned on having exactly m branches; denote this random limit by
$\widehat{{\mathcal T}}$
conditioned on having exactly m branches; denote this random limit by
![]() $({\mathcal T}_1,\dots,{\mathcal T}_m)$
. By the Skorohod coupling theorem [Reference Kallenberg32, Theorem 4.30], we may (for simplicity) assume that this convergence is a.s. The convergence here is in the local topology used in [Reference Janson30], which means [Reference Janson30, Lemma 6.2] that for any fixed
$({\mathcal T}_1,\dots,{\mathcal T}_m)$
. By the Skorohod coupling theorem [Reference Kallenberg32, Theorem 4.30], we may (for simplicity) assume that this convergence is a.s. The convergence here is in the local topology used in [Reference Janson30], which means [Reference Janson30, Lemma 6.2] that for any fixed
![]() $\ell\geqslant1$
, if
$\ell\geqslant1$
, if
![]() $T^{[\ell]}$
denotes the tree T truncated at height
$T^{[\ell]}$
denotes the tree T truncated at height
![]() $\ell$
, then a.s., for sufficiently large n,
$\ell$
, then a.s., for sufficiently large n,
![]() ${\mathcal T}^{{\textbf{p},[\ell]}}_{n,m;\,i}={\mathcal T}_i^{[\ell]}$
.
${\mathcal T}^{{\textbf{p},[\ell]}}_{n,m;\,i}={\mathcal T}_i^{[\ell]}$
.
The infinite tree
![]() $\widehat{{\mathcal T}}$
has exactly one infinite branch; thus, there exists a (random)
$\widehat{{\mathcal T}}$
has exactly one infinite branch; thus, there exists a (random)
![]() $j\leqslant m$
such that
$j\leqslant m$
such that
![]() ${\mathcal T}_j$
is infinite but
${\mathcal T}_j$
is infinite but
![]() ${\mathcal T}_i$
is finite for
${\mathcal T}_i$
is finite for
![]() $i\neq j$
. Truncating the trees at an
$i\neq j$
. Truncating the trees at an
![]() $\ell$
chosen larger than the heights
$\ell$
chosen larger than the heights
![]() $H({\mathcal T}_i)$
for all
$H({\mathcal T}_i)$
for all
![]() $i\neq j$
, we see that for large n,
$i\neq j$
, we see that for large n,
![]() ${\mathcal T}^{{\textbf{p}}}_{n,m;\,i}={\mathcal T}_i$
. Thus,
${\mathcal T}^{{\textbf{p}}}_{n,m;\,i}={\mathcal T}_i$
. Thus,
![]() $|{\mathcal T}^{{\textbf{p}}}_{n,m;\,i}|=O(1)$
for
$|{\mathcal T}^{{\textbf{p}}}_{n,m;\,i}|=O(1)$
for
![]() $i\neq j$
, and necessarily the remaining branch
$i\neq j$
, and necessarily the remaining branch
![]() ${\mathcal T}^{{\textbf{p}}}_{n,m;\,j}$
has size
${\mathcal T}^{{\textbf{p}}}_{n,m;\,j}$
has size
![]() $n-O(1)$
. Hence, for large enough n,
$n-O(1)$
. Hence, for large enough n,
![]() ${\mathcal T}^{{\textbf{p}}}_{n,m;\,(1)}={\mathcal T}^{{\textbf{p}}}_{n,m;\,j}$
.
${\mathcal T}^{{\textbf{p}}}_{n,m;\,(1)}={\mathcal T}^{{\textbf{p}}}_{n,m;\,j}$
.
Consequently,
![]() ${\mathcal T}^{{\textbf{p}}}_{n,m;\,(2)},\dots,{\mathcal T}^{{\textbf{p}}}_{n,m;\,(m)}$
converge a.s., and thus in distribution, to the
${\mathcal T}^{{\textbf{p}}}_{n,m;\,(2)},\dots,{\mathcal T}^{{\textbf{p}}}_{n,m;\,(m)}$
converge a.s., and thus in distribution, to the
![]() $m-1$
finite branches of
$m-1$
finite branches of
![]() $\widehat{{\mathcal T}}$
, arranged in decreasing order and conditioned on
$\widehat{{\mathcal T}}$
, arranged in decreasing order and conditioned on
![]() $\mathcal E_m$
. In particular, their sizes converge in distribution and are thus
$\mathcal E_m$
. In particular, their sizes converge in distribution and are thus
![]() $O_{\textrm{p}}(1)$
.
$O_{\textrm{p}}(1)$
.
We assumed for simplicity
![]() $p_m>0$
. In general, we may select a rooted tree T with
$p_m>0$
. In general, we may select a rooted tree T with
![]() $\geqslant m$
leaves, such that
$\geqslant m$
leaves, such that
![]() $p_{d^+(v)}>0$
for every
$p_{d^+(v)}>0$
for every
![]() $v\in T$
. Fix m leaves
$v\in T$
. Fix m leaves
![]() $v_1,\dots,v_m$
in T, and consider the conditioned Galton–Watson tree
$v_1,\dots,v_m$
in T, and consider the conditioned Galton–Watson tree
![]() ${\mathcal T}^{{\textbf{p}}}_{n+|T|-m}$
conditioned on the event
${\mathcal T}^{{\textbf{p}}}_{n+|T|-m}$
conditioned on the event
![]() $\mathcal E_T$
that it consists of T with subtrees added at
$\mathcal E_T$
that it consists of T with subtrees added at
![]() $v_1,\dots,v_m$
. Then these subtrees form a conditioned Galton–Watson forest
$v_1,\dots,v_m$
. Then these subtrees form a conditioned Galton–Watson forest
![]() ${\mathcal T}^{{\textbf{p}}}_{n,m}$
, and we can argue as above, conditioning
${\mathcal T}^{{\textbf{p}}}_{n,m}$
, and we can argue as above, conditioning
![]() $\widehat{{\mathcal T}}$
on
$\widehat{{\mathcal T}}$
on
![]() $\mathcal E_T$
.
$\mathcal E_T$
.
This completes the proof when
![]() $\mu(\textbf{p})=1$
. If
$\mu(\textbf{p})=1$
. If
![]() $\mu(\textbf{p})>1$
, there always exists an equivalent probability weight
$\mu(\textbf{p})>1$
, there always exists an equivalent probability weight
![]() $\tilde{\textbf{p}}$
with
$\tilde{\textbf{p}}$
with
![]() $\mu(\tilde{\textbf{p}})=1$
, and the result follows. If
$\mu(\tilde{\textbf{p}})=1$
, and the result follows. If
![]() $\mu(\textbf{p})<1$
, the same may hold, and if it does not hold, then there is a similar infinite limit tree
$\mu(\textbf{p})<1$
, the same may hold, and if it does not hold, then there is a similar infinite limit tree
![]() $\widehat{{\mathcal T}}$
[Reference Janson30, Theorem 7.1]; in this case,
$\widehat{{\mathcal T}}$
[Reference Janson30, Theorem 7.1]; in this case,
![]() $\widehat{{\mathcal T}}$
has one vertex of infinite degree, but the proof above holds with minor modifications.
$\widehat{{\mathcal T}}$
has one vertex of infinite degree, but the proof above holds with minor modifications.
Remark 3.2. The proof shows that in the case
![]() $\mu(\textbf{p})=1$
, the small trees
$\mu(\textbf{p})=1$
, the small trees
![]() ${\mathcal T}^{{\textbf{p}}}_{n,m;\,(2)},\dots,{\mathcal T}^{{\textbf{p}}}_{n,m;\,(m)}$
in the forest converge in distribution to
${\mathcal T}^{{\textbf{p}}}_{n,m;\,(2)},\dots,{\mathcal T}^{{\textbf{p}}}_{n,m;\,(m)}$
in the forest converge in distribution to
![]() $m-1$
independent copies of the unconditioned Galton–Watson tree
$m-1$
independent copies of the unconditioned Galton–Watson tree
![]() ${\mathcal T}^{{\textbf{p}}}$
, arranged in decreasing order. More generally, the small trees converge in distribution to independent Galton–Watson trees for a probability distribution equivalent to
${\mathcal T}^{{\textbf{p}}}$
, arranged in decreasing order. More generally, the small trees converge in distribution to independent Galton–Watson trees for a probability distribution equivalent to
![]() $\textbf{p}$
. (This too was shown in [38, Lemma 5.7(iii)] under stronger assumptions.)
$\textbf{p}$
. (This too was shown in [38, Lemma 5.7(iii)] under stronger assumptions.)
Remark 3.3. In the standard case
![]() $\mu(\textbf{p})=1$
,
$\mu(\textbf{p})=1$
,
![]() $\sigma^2(\textbf{p})<\infty$
, it is also easy to show Lemma 3.1 using the fact
$\sigma^2(\textbf{p})<\infty$
, it is also easy to show Lemma 3.1 using the fact
![]() ${\mathbb P{}}(|{\mathcal T}^{{\textbf{p}}}|=n)\sim c n^{-3/2}$
, for some
${\mathbb P{}}(|{\mathcal T}^{{\textbf{p}}}|=n)\sim c n^{-3/2}$
, for some
![]() $c>0$
, which is a well-known consequence of the local limit theorem, cf. (36)–(37).
$c>0$
, which is a well-known consequence of the local limit theorem, cf. (36)–(37).
Problem 3.4. A simply generated forest
![]() ${\mathcal T}^{{\boldsymbol{\phi}}}_{n,m}$
is covered by Lemma 3.1 when the generating function (29) has positive radius of convergence, since then it is equivalent to a conditioned Galton–Watson forest. We conjecture that Lemma 3.1 holds for simply generated forests also in the case when the generating function has radius of convergence 0, but we leave this as an open problem.
${\mathcal T}^{{\boldsymbol{\phi}}}_{n,m}$
is covered by Lemma 3.1 when the generating function (29) has positive radius of convergence, since then it is equivalent to a conditioned Galton–Watson forest. We conjecture that Lemma 3.1 holds for simply generated forests also in the case when the generating function has radius of convergence 0, but we leave this as an open problem.
4. Modified simply generated trees
One frequently meets random trees where the root has a special distribution, see, for example [Reference Kortchemski and Marzouk38, Reference Marckert and Panholzer41]. Thus, let
![]() $\boldsymbol{\phi}$
and
$\boldsymbol{\phi}$
and
![]() $\boldsymbol{\phi}^0$
be two weight sequences, where
$\boldsymbol{\phi}^0$
be two weight sequences, where
![]() $\boldsymbol{\phi}$
is as above, and
$\boldsymbol{\phi}$
is as above, and
![]() $\boldsymbol{\phi}^0=(\phi^0_k)_0^\infty$
satisfies
$\boldsymbol{\phi}^0=(\phi^0_k)_0^\infty$
satisfies
![]() $\phi^0_k\geqslant0$
, with strict inequality for at least one k. We modify (26) and now define the weight of a tree
$\phi^0_k\geqslant0$
, with strict inequality for at least one k. We modify (26) and now define the weight of a tree
![]() $T\in\mathfrak{T}$
as
$T\in\mathfrak{T}$
as
The random modified simply generated tree
![]() ${\mathcal T}^{{\boldsymbol{\phi}},{\boldsymbol{\phi}^0}}_n$
is defined as in (27), using the modified weight (31).
${\mathcal T}^{{\boldsymbol{\phi}},{\boldsymbol{\phi}^0}}_n$
is defined as in (27), using the modified weight (31).
We say that a pair
![]() $(\boldsymbol{\phi}',\boldsymbol{\phi}^{0\prime})$
is equivalent to
$(\boldsymbol{\phi}',\boldsymbol{\phi}^{0\prime})$
is equivalent to
![]() $(\boldsymbol{\phi},\boldsymbol{\phi}^0)$
if (28) holds and similarly
$(\boldsymbol{\phi},\boldsymbol{\phi}^0)$
if (28) holds and similarly
It is important that the same b is used in (28) and (32), while a and
![]() $a_0$
may be different. It is easy to see that equivalent pairs of weight sequences define the same modified simply generated tree.
$a_0$
may be different. It is easy to see that equivalent pairs of weight sequences define the same modified simply generated tree.
Similarly, given two probability sequences
![]() $\textbf{p}=(p_k)_0^\infty$
and
$\textbf{p}=(p_k)_0^\infty$
and
![]() $\textbf{p}^0=({p}^0_k)_0^\infty$
, we define the modified Galton–Watson tree
$\textbf{p}^0=({p}^0_k)_0^\infty$
, we define the modified Galton–Watson tree
![]() ${\mathcal T}^{{\textbf{p},\textbf{p}^0}}$
and conditioned modified Galton–Watson tree
${\mathcal T}^{{\textbf{p},\textbf{p}^0}}$
and conditioned modified Galton–Watson tree
![]() ${\mathcal T}^{{\textbf{p},\textbf{p}^0}}_n$
as in Section 3.2, but now giving children to the root with distribution
${\mathcal T}^{{\textbf{p},\textbf{p}^0}}_n$
as in Section 3.2, but now giving children to the root with distribution
![]() $\textbf{p}^0$
, and to everyone else with distribution
$\textbf{p}^0$
, and to everyone else with distribution
![]() $\textbf{p}$
.
$\textbf{p}$
.
Again, as indicated by our notation, we have an equality: the conditioned modified Galton–Watson tree
![]() ${\mathcal T}^{{\textbf{p},\textbf{p}^0}}_n$
equals the modified simply generated tree with weight sequences
${\mathcal T}^{{\textbf{p},\textbf{p}^0}}_n$
equals the modified simply generated tree with weight sequences
![]() $\textbf{p}$
and
$\textbf{p}$
and
![]() $\textbf{p}^0$
. Conversely, if two weight sequences
$\textbf{p}^0$
. Conversely, if two weight sequences
![]() $\boldsymbol{\phi}$
and
$\boldsymbol{\phi}$
and
![]() $\boldsymbol{\phi}^0$
both have positive radius of convergence, then it is possible (by taking b small enough) to find equivalent weight sequences
$\boldsymbol{\phi}^0$
both have positive radius of convergence, then it is possible (by taking b small enough) to find equivalent weight sequences
![]() $\boldsymbol{\phi}'$
and
$\boldsymbol{\phi}'$
and
![]() $\boldsymbol{\phi}^{0\prime}$
that are probability sequences, and thus
$\boldsymbol{\phi}^{0\prime}$
that are probability sequences, and thus
![]() ${\mathcal T}^{{\boldsymbol{\phi},\boldsymbol{\phi}^0}}_n= {\mathcal T}^{{\boldsymbol{\phi}',\boldsymbol{\phi}^{0\prime}}}_n$
can be interpreted as a conditioned modified Galton–Watson tree.
${\mathcal T}^{{\boldsymbol{\phi},\boldsymbol{\phi}^0}}_n= {\mathcal T}^{{\boldsymbol{\phi}',\boldsymbol{\phi}^{0\prime}}}_n$
can be interpreted as a conditioned modified Galton–Watson tree.
Lemma 4.1. Consider a modified simply generated tree
![]() ${\mathcal T}^{{\boldsymbol{\phi},\boldsymbol{\phi}^0}}_n$
and denote its branches by
${\mathcal T}^{{\boldsymbol{\phi},\boldsymbol{\phi}^0}}_n$
and denote its branches by
![]() $T_1,\dots,T_{d(o)}$
.
$T_1,\dots,T_{d(o)}$
.
-
(i) Conditioned on the root degree d(o), the branches form a simply generated forest
 ${\mathcal T}^{{\boldsymbol{\phi}}}_{n-1,d(o)}$
.
${\mathcal T}^{{\boldsymbol{\phi}}}_{n-1,d(o)}$
. -
(ii) Conditioned on the root degree d(o) and the sizes
 $|T_i|$
of the branches, the branches are independent simply generated trees
$|T_i|$
of the branches, the branches are independent simply generated trees
 ${\mathcal T}^{{\boldsymbol{\phi}}}_{|T_i|}$
.
${\mathcal T}^{{\boldsymbol{\phi}}}_{|T_i|}$
.
Proof. Exercise.
Note that Lemma 4.1 applies also to the simply generated tree
![]() ${\mathcal T}^{{\boldsymbol{\phi}}}_n$
(by taking
${\mathcal T}^{{\boldsymbol{\phi}}}_n$
(by taking
![]() $\boldsymbol{\phi}^0=\boldsymbol{\phi}$
). Thus, conditioned on the root degree the branches have the same distribution for
$\boldsymbol{\phi}^0=\boldsymbol{\phi}$
). Thus, conditioned on the root degree the branches have the same distribution for
![]() ${\mathcal T}^{{\boldsymbol{\phi}}}_n$
and
${\mathcal T}^{{\boldsymbol{\phi}}}_n$
and
![]() ${\mathcal T}^{{\boldsymbol{\phi},\boldsymbol{\phi}^0}}_n$
. Hence, the distribution of the root degree is of central importance. The following lemma is partly shown by [Reference Kortchemski and Marzouk38, Proposition 5.6] in greater generality (the stable case), although we add the estimate (35).
${\mathcal T}^{{\boldsymbol{\phi},\boldsymbol{\phi}^0}}_n$
. Hence, the distribution of the root degree is of central importance. The following lemma is partly shown by [Reference Kortchemski and Marzouk38, Proposition 5.6] in greater generality (the stable case), although we add the estimate (35).
Lemma 4.2. (mainly Kortchemski and Marzouk [Reference Kortchemski and Marzouk38]) Suppose that
![]() ${\textbf{p}}$
is a probability sequence with mean
${\textbf{p}}$
is a probability sequence with mean
![]() $\mu({\textbf{p}})=1$
and variance
$\mu({\textbf{p}})=1$
and variance
![]() $\sigma^2({\textbf{p}})\in(0,\infty)$
and that
$\sigma^2({\textbf{p}})\in(0,\infty)$
and that
![]() ${\textbf{p}}^0$
is a probability sequence with finite mean
${\textbf{p}}^0$
is a probability sequence with finite mean
![]() $\mu({\textbf{p}}^0)$
. Then the root degree d(o) in the conditioned modified Galton–Watson tree
$\mu({\textbf{p}}^0)$
. Then the root degree d(o) in the conditioned modified Galton–Watson tree
![]() ${\mathcal T}_n^{{{\textbf{p}},{\textbf{p}}^0}}$
converges in distribution to a random variable
${\mathcal T}_n^{{{\textbf{p}},{\textbf{p}}^0}}$
converges in distribution to a random variable
![]() $\widetilde D$
with distribution
$\widetilde D$
with distribution
 \begin{align} {\mathbb P{}}(\widetilde D=k)= \frac{k{p}^0_k}{\sum_{j=1}^\infty j{p}^0_j}= \frac{k{p}^0_k}{\mu({\textbf{p}}^0)}.\end{align}
\begin{align} {\mathbb P{}}(\widetilde D=k)= \frac{k{p}^0_k}{\sum_{j=1}^\infty j{p}^0_j}= \frac{k{p}^0_k}{\mu({\textbf{p}}^0)}.\end{align}
In other words, for every fixed
![]() $k\geqslant0$
,
$k\geqslant0$
,
Moreover, if n is large enough, we have uniformly
As a consequence,
![]() ${\mathbb E{}}\widetilde D<\infty$
if and only if
${\mathbb E{}}\widetilde D<\infty$
if and only if
![]() $\sigma^2(\textbf{p}^0)<\infty$
.
$\sigma^2(\textbf{p}^0)<\infty$
.
Proof. This uses well-known standard arguments, but we give a full proof for completeness; see also [Reference Kortchemski and Marzouk38]. Let D be the root degree in the modified Galton–Watson tree
![]() ${\mathcal T}^{{\textbf{p},\textbf{p}^0}}$
. If
${\mathcal T}^{{\textbf{p},\textbf{p}^0}}$
. If
![]() $D=k$
, then the rest of the tree consists of k independent copies of
$D=k$
, then the rest of the tree consists of k independent copies of
![]() ${\mathcal T}^{{\textbf{p}}}$
. Thus, the conditional probability
${\mathcal T}^{{\textbf{p}}}$
. Thus, the conditional probability
![]() ${\mathbb P{}}\bigl({|{\mathcal T}^{{\textbf{p},\textbf{p}^0}}|=n\mid D=k}\bigr)$
equals the probability that a Galton–Watson process started with k individuals has in total
${\mathbb P{}}\bigl({|{\mathcal T}^{{\textbf{p},\textbf{p}^0}}|=n\mid D=k}\bigr)$
equals the probability that a Galton–Watson process started with k individuals has in total
![]() $n-1$
individuals; hence, by a formula by Dwass [Reference Dwass24], see e.g. [Reference Janson30, Section 15] and the further references there,
$n-1$
individuals; hence, by a formula by Dwass [Reference Dwass24], see e.g. [Reference Janson30, Section 15] and the further references there,
where
![]() $S_{n-1}$
denotes the sum of
$S_{n-1}$
denotes the sum of
![]() $n-1$
independent random variables with distribution
$n-1$
independent random variables with distribution
![]() $\textbf{p}$
.
$\textbf{p}$
.
Suppose for simplicity that the distribution
![]() $\textbf{p}$
is aperiodic, i.e., not supported on any subgroup
$\textbf{p}$
is aperiodic, i.e., not supported on any subgroup
![]() $d\mathbb N$
. (The general case follows similarly using standard modifications.) It then follows by the local limit theorem, see e.g. [Reference Kolchin36, Theorem 1.4.2] or [Reference Petrov46, Theorem VII.1], that, as
$d\mathbb N$
. (The general case follows similarly using standard modifications.) It then follows by the local limit theorem, see e.g. [Reference Kolchin36, Theorem 1.4.2] or [Reference Petrov46, Theorem VII.1], that, as
![]() ${{n\to\infty}}$
,
${{n\to\infty}}$
,
uniformly in k. Consequently, combining (36) and (37) with
![]() ${\mathbb P{}}(D=k)={p}^0_k$
,
${\mathbb P{}}(D=k)={p}^0_k$
,
 \begin{align} {\mathbb P{}}\bigl({|{\mathcal T}^{{\textbf{p},\textbf{p}^0}}|=n \text{ and } D=k}\bigr)&=\frac{k{p}^0_k}{n-1}{\mathbb P{}}\bigl({S_{n-1}=n-k-1}\bigr)\notag\\&= c\frac{k{p}^0_k}{n^{3/2}}\bigl({e^{-k^2/(2n\sigma^2)}+o(1)}\bigr),\end{align}
\begin{align} {\mathbb P{}}\bigl({|{\mathcal T}^{{\textbf{p},\textbf{p}^0}}|=n \text{ and } D=k}\bigr)&=\frac{k{p}^0_k}{n-1}{\mathbb P{}}\bigl({S_{n-1}=n-k-1}\bigr)\notag\\&= c\frac{k{p}^0_k}{n^{3/2}}\bigl({e^{-k^2/(2n\sigma^2)}+o(1)}\bigr),\end{align}
uniformly in k, where
![]() $c\,:\!=\,(2\pi\sigma^2)^{-1/2}$
.
$c\,:\!=\,(2\pi\sigma^2)^{-1/2}$
.
Summing over k we find as
![]() ${{n\to\infty}}$
, using
${{n\to\infty}}$
, using
![]() $\sum k{p}^0_k<\infty$
and monotone convergence,
$\sum k{p}^0_k<\infty$
and monotone convergence,
 \begin{align} {\mathbb P{}}\bigl({|{\mathcal T}^{{\textbf{p},\textbf{p}^0}}|=n}\bigr)&=\frac{c}{n^{3/2}}\Bigl({\sum_{k=1}^\infty {k{p}^0_k}e^{-k^2/(2n\sigma^2)}+o(1)}\Bigr)\sim \frac{c}{n^{3/2}}\sum_{k=1}^\infty {k{p}^0_k}.\end{align}
\begin{align} {\mathbb P{}}\bigl({|{\mathcal T}^{{\textbf{p},\textbf{p}^0}}|=n}\bigr)&=\frac{c}{n^{3/2}}\Bigl({\sum_{k=1}^\infty {k{p}^0_k}e^{-k^2/(2n\sigma^2)}+o(1)}\Bigr)\sim \frac{c}{n^{3/2}}\sum_{k=1}^\infty {k{p}^0_k}.\end{align}
Thus, combining (38) and (39), for any fixed
![]() $k\geqslant1$
, as
$k\geqslant1$
, as
![]() ${{n\to\infty}}$
,
${{n\to\infty}}$
,
 \begin{align} {\mathbb P{}}\bigl({D=k\mid|{\mathcal T}^{{\textbf{p},\textbf{p}^0}}|=n}\bigr)&=\frac{ {\mathbb P{}}\bigl({|{\mathcal T}^{{\textbf{p},\textbf{p}^0}}|=n\text{ and } D=k}\bigr)}{ {\mathbb P{}}\bigl({|{\mathcal T}^{{\textbf{p},\textbf{p}^0}}|=n}\bigr)}\notag\\&\to \frac{k{p}^0_k}{\sum_{j=1}^\infty j{p}^0_j}.\end{align}
\begin{align} {\mathbb P{}}\bigl({D=k\mid|{\mathcal T}^{{\textbf{p},\textbf{p}^0}}|=n}\bigr)&=\frac{ {\mathbb P{}}\bigl({|{\mathcal T}^{{\textbf{p},\textbf{p}^0}}|=n\text{ and } D=k}\bigr)}{ {\mathbb P{}}\bigl({|{\mathcal T}^{{\textbf{p},\textbf{p}^0}}|=n}\bigr)}\notag\\&\to \frac{k{p}^0_k}{\sum_{j=1}^\infty j{p}^0_j}.\end{align}
The limits on the right-hand side sum to 1, and thus the result (33) follows.
Moreover, (38) and (39) also yield
 \begin{align} {\mathbb P{}}\bigl({D=k\mid|{\mathcal T}^{{\textbf{p},\textbf{p}^0}}|=n}\bigr)&=\frac{ {\mathbb P{}}\bigl({|{\mathcal T}^{{\textbf{p},\textbf{p}^0}}|=n\text{ and } D=k}\bigr)}{ {\mathbb P{}}\bigl({|{\mathcal T}^{{\textbf{p},\textbf{p}^0}}|=n}\bigr)}\notag\\&\leqslant \frac{k{p}^0_k}{\sum_{j=1}^\infty j{p}^0_j}\bigl({1+o(1)}\bigr),\end{align}
\begin{align} {\mathbb P{}}\bigl({D=k\mid|{\mathcal T}^{{\textbf{p},\textbf{p}^0}}|=n}\bigr)&=\frac{ {\mathbb P{}}\bigl({|{\mathcal T}^{{\textbf{p},\textbf{p}^0}}|=n\text{ and } D=k}\bigr)}{ {\mathbb P{}}\bigl({|{\mathcal T}^{{\textbf{p},\textbf{p}^0}}|=n}\bigr)}\notag\\&\leqslant \frac{k{p}^0_k}{\sum_{j=1}^\infty j{p}^0_j}\bigl({1+o(1)}\bigr),\end{align}
uniformly in k. In particular, (35) holds for all k if n is large enough.
Finally, by (33),
![]() ${\mathbb E{}}\widetilde D=\sum k{\mathbb P{}}(\widetilde D=k)<\infty$
if and only if
${\mathbb E{}}\widetilde D=\sum k{\mathbb P{}}(\widetilde D=k)<\infty$
if and only if
![]() $\sum_k k^2{p}^0_k<\infty$
.
$\sum_k k^2{p}^0_k<\infty$
.
It follows from Lemma 4.2 that the tree is overwhelmingly dominated by one branch. (Again, this was shown by Kortchemski and Marzouk [Reference Kortchemski and Marzouk38] in greater generality.)
Lemma 4.3. (essentially Kortchemski and Marzouk [38, Proposition 5.6]) Suppose that
![]() ${\textbf{p}}$
is a probability sequence with mean
${\textbf{p}}$
is a probability sequence with mean
![]() $\mu({\textbf{p}})=1$
and variance
$\mu({\textbf{p}})=1$
and variance
![]() $\sigma^2({\textbf{p}})\in(0,\infty)$
and that
$\sigma^2({\textbf{p}})\in(0,\infty)$
and that
![]() ${\textbf{p}}^0$
is a probability sequence with finite mean
${\textbf{p}}^0$
is a probability sequence with finite mean
![]() $\mu({\textbf{p}}^0)$
. Let
$\mu({\textbf{p}}^0)$
. Let
![]() ${\mathcal T}_{n,(1)},\dots,{\mathcal T}_{n,({d(o)})}$
be the branches of
${\mathcal T}_{n,(1)},\dots,{\mathcal T}_{n,({d(o)})}$
be the branches of
![]() ${\mathcal T}^{{{\textbf{p}},{\textbf{p}}^0}}_n$
arranged in decreasing order. Then
${\mathcal T}^{{{\textbf{p}},{\textbf{p}}^0}}_n$
arranged in decreasing order. Then
Proof. Let
![]() $D_n=d(o)$
and condition on
$D_n=d(o)$
and condition on
![]() $D_n=m$
, for a fixed m. Then, by Lemmas 4.1 and 3.1, (42) holds. In other words, for every
$D_n=m$
, for a fixed m. Then, by Lemmas 4.1 and 3.1, (42) holds. In other words, for every
![]() $\varepsilon>0$
, there exists
$\varepsilon>0$
, there exists
![]() $C_{m,\varepsilon}$
such that
$C_{m,\varepsilon}$
such that
By Lemma 4.2,
![]() $D_n\overset{\textrm{d}}{\longrightarrow}\widetilde D$
, and thus
$D_n\overset{\textrm{d}}{\longrightarrow}\widetilde D$
, and thus
![]() $(D_n)_n$
is tight, i.e.,
$(D_n)_n$
is tight, i.e.,
![]() $O_{\textrm{p}}(1)$
, so there exists M such that
$O_{\textrm{p}}(1)$
, so there exists M such that
![]() ${\mathbb P{}}(D_n>M)<\varepsilon$
for all n. Consequently, if
${\mathbb P{}}(D_n>M)<\varepsilon$
for all n. Consequently, if
![]() $C_{\varepsilon}\,:\!=\,\max_{m\leqslant M}C_{m,\varepsilon}$
,
$C_{\varepsilon}\,:\!=\,\max_{m\leqslant M}C_{m,\varepsilon}$
,
which completes the proof.
Lemmas 4.1–4.3 make it possible to transfer many results that are known for simply generated trees (conditioned Galton–Watson trees) to the modified version. See Section 9 for a few examples.
Problem 4.4. Does Lemma 4.2 (and thus Lemma 4.3) hold without assuming finite variance
![]() $\sigma^2(\textbf{p})<\infty$
. i.e., assuming only
$\sigma^2(\textbf{p})<\infty$
. i.e., assuming only
![]() $\mu(\textbf{p})=1$
and
$\mu(\textbf{p})=1$
and
![]() $\mu(\textbf{p}^0)<\infty$
? As said above, (33) was shown also when the variance is infinite by Kortchemski and Marzouk [Reference Kortchemski and Marzouk38], but they then assume that
$\mu(\textbf{p}^0)<\infty$
? As said above, (33) was shown also when the variance is infinite by Kortchemski and Marzouk [Reference Kortchemski and Marzouk38], but they then assume that
![]() $\textbf{p}$
is in the domain of attraction of a stable distribution. What happens without this regularity assumption?
$\textbf{p}$
is in the domain of attraction of a stable distribution. What happens without this regularity assumption?
Remark 4.5. We assume in Lemma 4.2 that
![]() $\mu(\textbf{p}^0)<\infty$
. We claim that if
$\mu(\textbf{p}^0)<\infty$
. We claim that if
![]() $\mu(\textbf{p}^0)=\infty$
, then
$\mu(\textbf{p}^0)=\infty$
, then
![]() $d(o)\overset{\textrm{p}}{\longrightarrow}\infty$
; in other words,
$d(o)\overset{\textrm{p}}{\longrightarrow}\infty$
; in other words,
![]() ${\mathbb P{}}(d(o)=k)\to0$
for every fixed k, which can be seen as the natural interpretation of (33)–(34) in this case.
${\mathbb P{}}(d(o)=k)\to0$
for every fixed k, which can be seen as the natural interpretation of (33)–(34) in this case.
We sketch a proof. First, from (38) and Fatou’s lemma (for sums),
 \begin{align} \liminf_{{{n\to\infty}}}n^{3/2} {\mathbb P{}}\bigl({|{\mathcal T}^{{\textbf{p},\textbf{p}^0}}|=n}\bigr)&\geqslant\sum_{k=0}^\infty \liminf_{{{n\to\infty}}}n^{3/2} {\mathbb P{}}\bigl({|{\mathcal T}^{{\textbf{p},\textbf{p}^0}}|=n \text{ and } D=k}\bigr)\notag\\&=\sum_{k=0}^\infty c k{p}^0_k=\infty.\end{align}
\begin{align} \liminf_{{{n\to\infty}}}n^{3/2} {\mathbb P{}}\bigl({|{\mathcal T}^{{\textbf{p},\textbf{p}^0}}|=n}\bigr)&\geqslant\sum_{k=0}^\infty \liminf_{{{n\to\infty}}}n^{3/2} {\mathbb P{}}\bigl({|{\mathcal T}^{{\textbf{p},\textbf{p}^0}}|=n \text{ and } D=k}\bigr)\notag\\&=\sum_{k=0}^\infty c k{p}^0_k=\infty.\end{align}
In other words,
![]() $ n^{3/2} {\mathbb P{}}\bigl({|{\mathcal T}^{{\textbf{p},\textbf{p}^0}}|=n}\bigr)\to \infty$
. Then, (38) and (45) yield, for any fixed
$ n^{3/2} {\mathbb P{}}\bigl({|{\mathcal T}^{{\textbf{p},\textbf{p}^0}}|=n}\bigr)\to \infty$
. Then, (38) and (45) yield, for any fixed
![]() $k\geqslant0$
,
$k\geqslant0$
,
 \begin{align} {\mathbb P{}}\bigl({D =k \mid|{\mathcal T}^{{\textbf{p},\textbf{p}^0}}|=n}\bigr)&=\frac{ {\mathbb P{}}\bigl({|{\mathcal T}^{{\textbf{p},\textbf{p}^0}}|=n\text{ and } D=k}\bigr)}{ {\mathbb P{}}\bigl({|{\mathcal T}^{{\textbf{p},\textbf{p}^0}}|=n}\bigr)} \to 0.\end{align}
\begin{align} {\mathbb P{}}\bigl({D =k \mid|{\mathcal T}^{{\textbf{p},\textbf{p}^0}}|=n}\bigr)&=\frac{ {\mathbb P{}}\bigl({|{\mathcal T}^{{\textbf{p},\textbf{p}^0}}|=n\text{ and } D=k}\bigr)}{ {\mathbb P{}}\bigl({|{\mathcal T}^{{\textbf{p},\textbf{p}^0}}|=n}\bigr)} \to 0.\end{align}
This proves our claim.
5. Unrooted simply generated trees
We make definitions corresponding to Section 3 for unrooted trees. In this case, we consider labelled trees, so that we can distinguish the vertices. (This is not needed for ordered trees, since their vertices can be labelled canonically as described in Section 2.) Of course, we may then ignore the labelling when we want.
Let
![]() $(w_k)_0^\infty$
be a given sequence of non-negative weights, with
$(w_k)_0^\infty$
be a given sequence of non-negative weights, with
![]() $w_1>0$
and
$w_1>0$
and
![]() $w_k>0$
for some
$w_k>0$
for some
![]() $k\geqslant3$
. (The weight
$k\geqslant3$
. (The weight
![]() $w_0$
is needed only for the trivial case
$w_0$
is needed only for the trivial case
![]() $n=1$
and might be ignored. We may take
$n=1$
and might be ignored. We may take
![]() $w_0=0$
without essential loss of generality.)
$w_0=0$
without essential loss of generality.)
For any labelled tree
![]() $T\in\mathfrak{L}_n$
, now define the weight of T as
$T\in\mathfrak{L}_n$
, now define the weight of T as
Given
![]() $n\geqslant1$
, we define the random unrooted simply generated tree
$n\geqslant1$
, we define the random unrooted simply generated tree
![]() ${\mathcal T}^\circ_{n}={\mathcal T}^{\textbf{w},\circ}_{n}$
as a labelled tree in
${\mathcal T}^\circ_{n}={\mathcal T}^{\textbf{w},\circ}_{n}$
as a labelled tree in
![]() ${\mathcal L}_n$
, chosen randomly with probability proportional to the weight (47). (We consider only n such that at least one tree of positive weight exists.)
${\mathcal L}_n$
, chosen randomly with probability proportional to the weight (47). (We consider only n such that at least one tree of positive weight exists.)
Remark 5.1. Just as in the rooted case, replacing the weight sequence by an equivalent one (still defined as in (28)) gives the same random tree
![]() ${\mathcal T}^\circ_{n}$
.
${\mathcal T}^\circ_{n}$
.
In the following sections, we give three (related but different) relations with the more well-known rooted simply generated trees.
6. Mark a vertex
Let
![]() ${\mathcal T}^{\textbf{w},\circ}_{n}$
be a random unrooted simply generated tree as in Section 5 and mark one of its n vertices, chosen uniformly at random. Regard the marked vertex as a root and denote the resulting rooted tree by
${\mathcal T}^{\textbf{w},\circ}_{n}$
be a random unrooted simply generated tree as in Section 5 and mark one of its n vertices, chosen uniformly at random. Regard the marked vertex as a root and denote the resulting rooted tree by
![]() ${\mathcal T}^{\textbf{w},\bullet}_n$
.
${\mathcal T}^{\textbf{w},\bullet}_n$
.
Thus,
![]() ${\mathcal T}^{\textbf{w},\bullet}_n$
is a random unordered rooted tree, where an unordered rooted tree T has probability proportional to its weight given by (47).
${\mathcal T}^{\textbf{w},\bullet}_n$
is a random unordered rooted tree, where an unordered rooted tree T has probability proportional to its weight given by (47).
We make
![]() ${\mathcal T}^{\textbf{w},\bullet}_n$
ordered by ordering the children of each vertex uniformly at random; denote the resulting random labelled ordered rooted tree by
${\mathcal T}^{\textbf{w},\bullet}_n$
ordered by ordering the children of each vertex uniformly at random; denote the resulting random labelled ordered rooted tree by
![]() ${\mathcal T}^{\textbf{w},*}_n$
. Since each vertex v has
${\mathcal T}^{\textbf{w},*}_n$
. Since each vertex v has
![]() $d^+(v)!$
possible orders, the probability that
$d^+(v)!$
possible orders, the probability that
![]() ${\mathcal T}^{\textbf{w},*}_n$
equals a given ordered tree T is proportional to the weight
${\mathcal T}^{\textbf{w},*}_n$
equals a given ordered tree T is proportional to the weight
The tree
![]() ${\mathcal T}^{\textbf{w},*}_n$
is constructed as a labelled tree, but each ordered rooted tree
${\mathcal T}^{\textbf{w},*}_n$
is constructed as a labelled tree, but each ordered rooted tree
![]() $T\in\mathfrak{T}_n$
has the same number
$T\in\mathfrak{T}_n$
has the same number
![]() $n!$
of labellings, and they have the same weight (48) and thus appear with the same probability. Hence, we may forget the labelling and regard
$n!$
of labellings, and they have the same weight (48) and thus appear with the same probability. Hence, we may forget the labelling and regard
![]() ${\mathcal T}^{\textbf{w},*}_n$
as a random ordered tree in
${\mathcal T}^{\textbf{w},*}_n$
as a random ordered tree in
![]() $\mathfrak{T}_n$
, with probabilities proportional to the weight (48). This is the same as the weight (31) with
$\mathfrak{T}_n$
, with probabilities proportional to the weight (48). This is the same as the weight (31) with
Thus,
![]() ${\mathcal T}^{\textbf{w},*}_n={\mathcal T}^{{\boldsymbol{\phi},\boldsymbol{\phi}^0}}_n$
, the modified simply generated tree defined in Section 4.
${\mathcal T}^{\textbf{w},*}_n={\mathcal T}^{{\boldsymbol{\phi},\boldsymbol{\phi}^0}}_n$
, the modified simply generated tree defined in Section 4.
We recover
![]() ${\mathcal T}^{\textbf{w},\circ}_{n}$
from
${\mathcal T}^{\textbf{w},\circ}_{n}$
from
![]() ${\mathcal T}^{*}_n={\mathcal T}^{{\boldsymbol{\phi},\boldsymbol{\phi}^0}}_n$
by ignoring the root (and adding a uniformly random labelling). This yields thus a method to construct
${\mathcal T}^{*}_n={\mathcal T}^{{\boldsymbol{\phi},\boldsymbol{\phi}^0}}_n$
by ignoring the root (and adding a uniformly random labelling). This yields thus a method to construct
![]() ${\mathcal T}^{\textbf{w},\circ}_{n}$
.
${\mathcal T}^{\textbf{w},\circ}_{n}$
.
Example 6.1. Marckert and Panholzer [Reference Marckert and Panholzer41] studied uniformly random non-crossing trees of a given size n and found that if they are regarded as ordered rooted trees, then they have the same distribution as the conditioned modified Galton–Watson tree
![]() ${\mathcal T}^{{\textbf{p},\textbf{p}^0}}_n$
, where
${\mathcal T}^{{\textbf{p},\textbf{p}^0}}_n$
, where
These weights are equivalent to
![]() $\phi_k=k+1$
and
$\phi_k=k+1$
and
![]() $\phi^0_k=1$
, which are given by (49)–(50) with
$\phi^0_k=1$
, which are given by (49)–(50) with
![]() $w_k=k!$
. We may thus reformulate the result by Marckert and Panholzer [Reference Marckert and Panholzer41] as: A uniformly random non-crossing tree is the same as a random unrooted simply generated tree with weights
$w_k=k!$
. We may thus reformulate the result by Marckert and Panholzer [Reference Marckert and Panholzer41] as: A uniformly random non-crossing tree is the same as a random unrooted simply generated tree with weights
![]() $w_k=k!$
.
$w_k=k!$
.
More generally, Kortchemski and Marzouk [Reference Kortchemski and Marzouk38] studied simply generated non-crossing trees, which are random non-crossing trees with probability proportional to the weight (47) for some weight sequence
![]() $\textbf{w}=(w_k)_k$
, and showed that they (under a condition) are equivalent to conditioned modified Galton–Watson trees. In fact, for any weight sequence
$\textbf{w}=(w_k)_k$
, and showed that they (under a condition) are equivalent to conditioned modified Galton–Watson trees. In fact, for any weight sequence
![]() $\textbf{w}$
, the proofs in [Reference Marckert and Panholzer41, in particular Lemma 2] and [Reference Kortchemski and Marzouk38, in particular Proposition 2.1] show that the simply generated non-crossing tree, regarded as an ordered rooted tree, is the same as
$\textbf{w}$
, the proofs in [Reference Marckert and Panholzer41, in particular Lemma 2] and [Reference Kortchemski and Marzouk38, in particular Proposition 2.1] show that the simply generated non-crossing tree, regarded as an ordered rooted tree, is the same as
![]() ${\mathcal T}^{{\boldsymbol{\phi},\boldsymbol{\phi}^0}}_n$
with
${\mathcal T}^{{\boldsymbol{\phi},\boldsymbol{\phi}^0}}_n$
with
Thus, comparing with (49)–(50), it follows that the simply generated non-crossing tree is an unordered simply generated tree, with weight sequence
![]() $\overline{w}_k\,:\!=\,w_kk!$
.
$\overline{w}_k\,:\!=\,w_kk!$
.
Note that non-crossing trees are naturally defined as unrooted trees. A root is introduced in [Reference Kortchemski and Marzouk38, Reference Marckert and Panholzer41] for the analysis, which as said above makes the trees conditioned modified Galton–Watson trees (or, more generally, modified simply generated trees). This is precisely the marking of an unrooted simply generated tree discussed in the present section.
Remark 6.2. The constructions in this and the next section lead to simple relations of generating functions (not used here); see [Reference Berzunza Ojeda and Janson10, Appendix B].
7. Mark an edge
In the random unrooted tree
![]() ${\mathcal T}^{\textbf{w},\circ}_{n}$
, mark a (uniformly) random edge, and give it a direction; i.e., mark two adjacent vertices, say
${\mathcal T}^{\textbf{w},\circ}_{n}$
, mark a (uniformly) random edge, and give it a direction; i.e., mark two adjacent vertices, say
![]() $o_+$
and
$o_+$
and
![]() $o_-$
. Since each tree
$o_-$
. Since each tree
![]() ${\mathcal T}^{\textbf{w},\circ}_{n}$
has the same number
${\mathcal T}^{\textbf{w},\circ}_{n}$
has the same number
![]() $n-1$
of edges, the resulting marked tree
$n-1$
of edges, the resulting marked tree
![]() ${\mathcal T}^{\textbf{w},\bullet\bullet}_n$
is distributed over all labelled trees on [n] with a marked and directed edge with probabilities proportional to the weight (47).
${\mathcal T}^{\textbf{w},\bullet\bullet}_n$
is distributed over all labelled trees on [n] with a marked and directed edge with probabilities proportional to the weight (47).
Now ignore the marked edge, and regard the tree
![]() ${\mathcal T}^{\textbf{w},\bullet\bullet}_n$
as two rooted trees
${\mathcal T}^{\textbf{w},\bullet\bullet}_n$
as two rooted trees
![]() ${\mathcal T}_{n,1}$
and
${\mathcal T}_{n,1}$
and
![]() ${\mathcal T}_{n,2}$
with roots
${\mathcal T}_{n,2}$
with roots
![]() $o_+$
and
$o_+$
and
![]() $o_-$
, respectively. Furthermore, order randomly the children of each vertex in each of these rooted trees; this makes
$o_-$
, respectively. Furthermore, order randomly the children of each vertex in each of these rooted trees; this makes
![]() ${\mathcal T}_{n,1}$
and
${\mathcal T}_{n,1}$
and
![]() ${\mathcal T}_{n,2}$
a pair of ordered trees, and each pair
${\mathcal T}_{n,2}$
a pair of ordered trees, and each pair
![]() $(T_+,T_-)$
of labelled ordered rooted trees with
$(T_+,T_-)$
of labelled ordered rooted trees with
![]() $|T_+|+|T_-|=n$
and the labels
$|T_+|+|T_-|=n$
and the labels
![]() $1,\dots,n$
appears with probability proportional to
$1,\dots,n$
appears with probability proportional to
where, for a rooted tree T,
Using again the definition (49), we have by (26),
Moreover, since we now have ordered rooted trees, the vertices are distinguishable, and each pair
![]() $(T_+,T_-)$
of ordered trees with
$(T_+,T_-)$
of ordered trees with
![]() $|T_+|+|T_-|=n$
has the same number
$|T_+|+|T_-|=n$
has the same number
![]() $n!$
of labellings. Hence, we may ignore the labelling and regard the marked tree
$n!$
of labellings. Hence, we may ignore the labelling and regard the marked tree
![]() ${\mathcal T}^{\textbf{w},\bullet\bullet}_n$
as a pair of ordered trees
${\mathcal T}^{\textbf{w},\bullet\bullet}_n$
as a pair of ordered trees
![]() $({\mathcal T}_{n,1},{\mathcal T}_{n,2})$
with
$({\mathcal T}_{n,1},{\mathcal T}_{n,2})$
with
![]() $|{\mathcal T}_{n,1}|+|{\mathcal T}_{n,2}|=n$
and probabilities proportional to the weight given by (55) and (57). This means that
$|{\mathcal T}_{n,1}|+|{\mathcal T}_{n,2}|=n$
and probabilities proportional to the weight given by (55) and (57). This means that
![]() ${\mathcal T}_{n,1}$
and
${\mathcal T}_{n,1}$
and
![]() ${\mathcal T}_{n,2}$
, conditioned on their sizes, are two independent random rooted simply generated trees, with the weight sequence
${\mathcal T}_{n,2}$
, conditioned on their sizes, are two independent random rooted simply generated trees, with the weight sequence
![]() $\boldsymbol{\phi}$
given by (49); in other words,
$\boldsymbol{\phi}$
given by (49); in other words,
![]() $({\mathcal T}_{n,1},{\mathcal T}_{n,2})$
is a simply generated forest
$({\mathcal T}_{n,1},{\mathcal T}_{n,2})$
is a simply generated forest
![]() ${\mathcal T}^{{\boldsymbol{\phi}}}_{n,2}$
.
${\mathcal T}^{{\boldsymbol{\phi}}}_{n,2}$
.
Consequently, we can construct the random unrooted simply generated tree
![]() ${\mathcal T}^{\textbf{w},\circ}_{n}$
by taking two random rooted simply generated trees
${\mathcal T}^{\textbf{w},\circ}_{n}$
by taking two random rooted simply generated trees
![]() ${\mathcal T}_{n,1}$
and
${\mathcal T}_{n,1}$
and
![]() ${\mathcal T}_{n,2}$
constructed in this way, with the right distribution of their sizes, and joining their roots.
${\mathcal T}_{n,2}$
constructed in this way, with the right distribution of their sizes, and joining their roots.
Note that
![]() $|{\mathcal T}_{n,1}|=n-|{\mathcal T}_{n,2}|$
is random, with a distribution given by the construction above. More precisely, if
$|{\mathcal T}_{n,1}|=n-|{\mathcal T}_{n,2}|$
is random, with a distribution given by the construction above. More precisely, if
![]() $a_n$
is the total weight (57) summed over all ordered trees of order n, then
$a_n$
is the total weight (57) summed over all ordered trees of order n, then
Remark 7.1. If
![]() $\phi_2>0$
, we can alternatively describe the result as follows: Use the weight sequence
$\phi_2>0$
, we can alternatively describe the result as follows: Use the weight sequence
![]() $(\phi_k)_0^\infty$
given by (49) and take a random rooted simply generated tree
$(\phi_k)_0^\infty$
given by (49) and take a random rooted simply generated tree
![]() ${\mathcal T}^{{\boldsymbol{\phi}}}_{n+1}$
of order
${\mathcal T}^{{\boldsymbol{\phi}}}_{n+1}$
of order
![]() $n+1$
, conditioned on the root degree
$n+1$
, conditioned on the root degree
![]() $=2$
; remove the root and join its two neighbours to each other (this is the marked edge).
$=2$
; remove the root and join its two neighbours to each other (this is the marked edge).
If
![]() $\phi_2=0$
, we can instead take any
$\phi_2=0$
, we can instead take any
![]() $k>2$
with
$k>2$
with
![]() $\phi_k>0$
, and take a random rooted simply generated tree
$\phi_k>0$
, and take a random rooted simply generated tree
![]() ${\mathcal T}^{{\boldsymbol{\phi}}}_{n+k-1}$
of order
${\mathcal T}^{{\boldsymbol{\phi}}}_{n+k-1}$
of order
![]() $n+k-1$
, conditioned on the event that the root degree is k, and the
$n+k-1$
, conditioned on the event that the root degree is k, and the
![]() $k-2$
last children of the root are leaves; we remove the root and these children, and join the first two children.
$k-2$
last children of the root are leaves; we remove the root and these children, and join the first two children.
Remark 7.2. Suppose that the weight sequence
![]() $(\phi_j)_0^\infty$
given by (49) satisfies
$(\phi_j)_0^\infty$
given by (49) satisfies
![]() $\sum_{j=1}^\infty\phi_j=1$
, so
$\sum_{j=1}^\infty\phi_j=1$
, so
![]() $(\phi_j)_0^\infty$
is a probability distribution. (Note that a large class of examples can be expressed with such weights, see Remark 5.1.) Then the construction above can be stated as follows:
$(\phi_j)_0^\infty$
is a probability distribution. (Note that a large class of examples can be expressed with such weights, see Remark 5.1.) Then the construction above can be stated as follows:
Consider a Galton–Watson process with offspring distribution
![]() $(\phi_k)_0^\infty$
, starting with two individuals, and conditioned on the total progeny being n. This creates a forest with two trees; join their roots to obtain
$(\phi_k)_0^\infty$
, starting with two individuals, and conditioned on the total progeny being n. This creates a forest with two trees; join their roots to obtain
![]() ${\mathcal T}^{\textbf{w},\circ}_{n}$
.
${\mathcal T}^{\textbf{w},\circ}_{n}$
.
Note that it follows from the arguments above that if we mark the edge joining the two roots, then the marked edge will be distributed uniformly over all edges in the tree
![]() ${\mathcal T}^{\textbf{w},\circ}_{n}$
.
${\mathcal T}^{\textbf{w},\circ}_{n}$
.
In the construction above,
![]() ${\mathcal T}_{n,1}$
and
${\mathcal T}_{n,1}$
and
![]() ${\mathcal T}_{n,2}$
have the same distribution by symmetry. Now define
${\mathcal T}_{n,2}$
have the same distribution by symmetry. Now define
![]() ${\mathcal T}_{n,+}$
as the largest and
${\mathcal T}_{n,+}$
as the largest and
![]() ${\mathcal T}_{n,-}$
as the smallest of
${\mathcal T}_{n,-}$
as the smallest of
![]() ${\mathcal T}_{n,1}$
and
${\mathcal T}_{n,1}$
and
![]() ${\mathcal T}_{n,2}$
. The next lemma shows that (at least under a weak condition),
${\mathcal T}_{n,2}$
. The next lemma shows that (at least under a weak condition),
![]() ${\mathcal T}_{n,-}$
is stochastically bounded, so
${\mathcal T}_{n,-}$
is stochastically bounded, so
![]() ${\mathcal T}^{\textbf{w},\circ}_{n}$
is dominated by the subtree
${\mathcal T}^{\textbf{w},\circ}_{n}$
is dominated by the subtree
![]() ${\mathcal T}_{n,+}$
.
${\mathcal T}_{n,+}$
.
Lemma 7.3. Suppose that the generating function
![]() $\Phi(z)$
in (29) has a positive radius of convergence. Then, as
$\Phi(z)$
in (29) has a positive radius of convergence. Then, as
![]() ${{n\to\infty}}$
,
${{n\to\infty}}$
,
![]() ${\mathcal T}_{n,-}\overset{{d}}{\longrightarrow}{\mathcal T}^{{{\textbf{p}}}}$
, an unconditioned Galton–Watson tree with offspring distribution
${\mathcal T}_{n,-}\overset{{d}}{\longrightarrow}{\mathcal T}^{{{\textbf{p}}}}$
, an unconditioned Galton–Watson tree with offspring distribution
![]() ${\textbf{p}}$
equivalent to
${\textbf{p}}$
equivalent to
![]() $(\phi_k)_0^\infty$
. In particular,
$(\phi_k)_0^\infty$
. In particular,
![]() $|{\mathcal T}_{n,-}|=O_{{p}}(1)$
, and thus
$|{\mathcal T}_{n,-}|=O_{{p}}(1)$
, and thus
![]() $|{\mathcal T}_{n,+}|=n-O_{{p}}(1)$
.
$|{\mathcal T}_{n,+}|=n-O_{{p}}(1)$
.
Proof. This is a special case of Lemma 3.1, see also Remark 3.2.
As remarked in Problem 3.4, we conjecture that
![]() $|{\mathcal T}_{n,-}|=O_{\textrm{p}}(1)$
also when the generating function has radius of convergence 0, but we leave this as an open problem.
$|{\mathcal T}_{n,-}|=O_{\textrm{p}}(1)$
also when the generating function has radius of convergence 0, but we leave this as an open problem.
8. Mark a leaf
This differs from the preceding two sections in that we do not recover the distribution of
![]() ${\mathcal T}^{\textbf{w},\circ}_{n}$
exactly, but only asymptotically.
${\mathcal T}^{\textbf{w},\circ}_{n}$
exactly, but only asymptotically.
Let
![]() $N_0(T)$
be the number of leaves in an unrooted tree T. Let
$N_0(T)$
be the number of leaves in an unrooted tree T. Let
![]() $\widehat{{\mathcal T}}^{\textbf{w},\circ}_{n}$
be a random unrooted labelled tree with probability proportional to
$\widehat{{\mathcal T}}^{\textbf{w},\circ}_{n}$
be a random unrooted labelled tree with probability proportional to
![]() $N_0(T)w(T)$
; in other words, we bias the distribution of
$N_0(T)w(T)$
; in other words, we bias the distribution of
![]() ${\mathcal T}^{\textbf{w},\circ}_{n}$
by the factor
${\mathcal T}^{\textbf{w},\circ}_{n}$
by the factor
![]() $N_0(T)$
.
$N_0(T)$
.
Let
![]() $\widehat{{\mathcal T}}^{\textbf{w},\bullet}_{n}$
be the random rooted tree obtained by marking a uniformly random leaf in
$\widehat{{\mathcal T}}^{\textbf{w},\bullet}_{n}$
be the random rooted tree obtained by marking a uniformly random leaf in
![]() $\widehat{{\mathcal T}}^{\textbf{w},\circ}_{n}$
, regarding the marked leaf as the root. Then, any pair (T, o) with
$\widehat{{\mathcal T}}^{\textbf{w},\circ}_{n}$
, regarding the marked leaf as the root. Then, any pair (T, o) with
![]() $T\in\mathfrak{L}_n$
and
$T\in\mathfrak{L}_n$
and
![]() $o\in T$
with
$o\in T$
with
![]() $d(o)=1$
will be chosen as
$d(o)=1$
will be chosen as
![]() $\widehat{{\mathcal T}}^{\textbf{w},\bullet}_{n}$
and its root with probability proportional to the weight (47). We order the children of each vertex at random as in Sections 6 and 7, and obtain an ordered rooted tree
$\widehat{{\mathcal T}}^{\textbf{w},\bullet}_{n}$
and its root with probability proportional to the weight (47). We order the children of each vertex at random as in Sections 6 and 7, and obtain an ordered rooted tree
![]() $\widehat{{\mathcal T}}^{\textbf{w},*}_{n}$
. Then each tree with root degree 1 appears with probability proportional to (48).
$\widehat{{\mathcal T}}^{\textbf{w},*}_{n}$
. Then each tree with root degree 1 appears with probability proportional to (48).
Consequently, if we ignore the labelling,
![]() $\widehat{{\mathcal T}}^{\textbf{w},*}_{n}={\mathcal T}^{{\boldsymbol{\phi}},{\boldsymbol{\phi}^0}}_n$
, where
$\widehat{{\mathcal T}}^{\textbf{w},*}_{n}={\mathcal T}^{{\boldsymbol{\phi}},{\boldsymbol{\phi}^0}}_n$
, where
![]() $\boldsymbol{\phi}$
is given by (49), and
$\boldsymbol{\phi}$
is given by (49), and
![]() $\phi^0_k\,:\!=\,\delta_{k1}$
(with a Kronecker delta). Equivalently,
$\phi^0_k\,:\!=\,\delta_{k1}$
(with a Kronecker delta). Equivalently,
![]() $\widehat{{\mathcal T}}^{\textbf{w},*}_{n}$
has a root of degree 1, and its single branch is a
$\widehat{{\mathcal T}}^{\textbf{w},*}_{n}$
has a root of degree 1, and its single branch is a
![]() ${\mathcal T}^{{\boldsymbol{\phi}}}_{n-1}$
.
${\mathcal T}^{{\boldsymbol{\phi}}}_{n-1}$
.
Conversely, we may obtain
![]() $\widehat{{\mathcal T}}^{\textbf{w},\circ}_{n}$
from
$\widehat{{\mathcal T}}^{\textbf{w},\circ}_{n}$
from
![]() ${\mathcal T}^{{\boldsymbol{\phi}}}_{n-1}$
by adding a new root under the old one and then adding a random labelling.
${\mathcal T}^{{\boldsymbol{\phi}}}_{n-1}$
by adding a new root under the old one and then adding a random labelling.
Remark 8.1. The construction above can also be regarded as a variant of the one in Section 7, where we mark an edge such that one endpoint is a leaf. Then, in the notation there,
![]() $|{\mathcal T}_{n,-}|=1$
and
$|{\mathcal T}_{n,-}|=1$
and
![]() ${\mathcal T}_{n,+}={\mathcal T}^{{\boldsymbol{\phi}}}_{n-1}$
.
${\mathcal T}_{n,+}={\mathcal T}^{{\boldsymbol{\phi}}}_{n-1}$
.
As said above,
![]() $\widehat{{\mathcal T}}^{\textbf{w},\circ}_{n}$
does not have the distribution of
$\widehat{{\mathcal T}}^{\textbf{w},\circ}_{n}$
does not have the distribution of
![]() ${\mathcal T}^{\textbf{w},\circ}_{n}$
, but it is not far from it.
${\mathcal T}^{\textbf{w},\circ}_{n}$
, but it is not far from it.
Lemma 8.2. Let
![]() ${\textbf{w}}$
be any weight sequence. As
${\textbf{w}}$
be any weight sequence. As
![]() ${{n\to\infty}}$
, the total variation distance
${{n\to\infty}}$
, the total variation distance
![]() $d_{{TV}}(\widehat{{\mathcal T}}^{{\textbf{w}},\circ}_{n},{\mathcal T}^{{\textbf{w}},\circ}_{n})\to0$
. In other words, there exists a coupling such that
$d_{{TV}}(\widehat{{\mathcal T}}^{{\textbf{w}},\circ}_{n},{\mathcal T}^{{\textbf{w}},\circ}_{n})\to0$
. In other words, there exists a coupling such that
![]() ${\mathbb P{}}\bigl({\widehat{{\mathcal T}}^{{\textbf{w}},\circ}_{n}\neq{\mathcal T}^{{\textbf{w}},\circ}_{n}}\bigr)\to0$
.
${\mathbb P{}}\bigl({\widehat{{\mathcal T}}^{{\textbf{w}},\circ}_{n}\neq{\mathcal T}^{{\textbf{w}},\circ}_{n}}\bigr)\to0$
.
Proof. We may construct
![]() ${\mathcal T}^{\textbf{w},\circ}_{n}$
as in Section 7 from two random ordered trees
${\mathcal T}^{\textbf{w},\circ}_{n}$
as in Section 7 from two random ordered trees
![]() ${\mathcal T}_{n,+}$
and
${\mathcal T}_{n,+}$
and
![]() ${\mathcal T}_{n,-}$
, where
${\mathcal T}_{n,-}$
, where
![]() $|{\mathcal T}_{n,-}|=O_{\textrm{p}}(1)$
. Conditioned on
$|{\mathcal T}_{n,-}|=O_{\textrm{p}}(1)$
. Conditioned on
![]() $|{\mathcal T}_{n,-}|=\ell$
, for any fixed
$|{\mathcal T}_{n,-}|=\ell$
, for any fixed
![]() $\ell$
, we have
$\ell$
, we have
![]() ${\mathcal T}_{n,+}\overset{\textrm{d}}{=} {\mathcal T}^{{\boldsymbol{\phi}}}_{n-\ell}$
, where
${\mathcal T}_{n,+}\overset{\textrm{d}}{=} {\mathcal T}^{{\boldsymbol{\phi}}}_{n-\ell}$
, where
![]() $\boldsymbol{\phi}$
is given by (49). Thus, by [Reference Janson30, Theorem 7.11] (see comments there for earlier references to special cases, and to further results), as
$\boldsymbol{\phi}$
is given by (49). Thus, by [Reference Janson30, Theorem 7.11] (see comments there for earlier references to special cases, and to further results), as
![]() ${{n\to\infty}}$
, conditioned on
${{n\to\infty}}$
, conditioned on
![]() $|{\mathcal T}_{n,-}|=\ell$
for any fixed
$|{\mathcal T}_{n,-}|=\ell$
for any fixed
![]() $\ell$
,
$\ell$
,
for some constant
![]() $\pi_0>0$
. (If
$\pi_0>0$
. (If
![]() $\boldsymbol{\phi}$
is a probability sequence, then
$\boldsymbol{\phi}$
is a probability sequence, then
![]() $\pi_0=\phi_0.)$
Furthermore,
$\pi_0=\phi_0.)$
Furthermore,
![]() $N_0({\mathcal T}^{\textbf{w},\circ}_{n})=N_0({\mathcal T}_{n,+})+N_0({\mathcal T}_{n,-})=N_0({\mathcal T}_{n,+})+O(1)$
, since
$N_0({\mathcal T}^{\textbf{w},\circ}_{n})=N_0({\mathcal T}_{n,+})+N_0({\mathcal T}_{n,-})=N_0({\mathcal T}_{n,+})+O(1)$
, since
![]() $N_0({\mathcal T}_{n,-})\leqslant|{\mathcal T}_{n,-}|=\ell$
. Consequently, still conditioned on
$N_0({\mathcal T}_{n,-})\leqslant|{\mathcal T}_{n,-}|=\ell$
. Consequently, still conditioned on
![]() $|{\mathcal T}_{n,-}|=\ell$
for any fixed
$|{\mathcal T}_{n,-}|=\ell$
for any fixed
![]() $\ell$
,
$\ell$
,
Since
![]() $ |{\mathcal T}_{n,-}|=O_{\textrm{p}}(1)$
, it follows that (60) holds also unconditionally.
$ |{\mathcal T}_{n,-}|=O_{\textrm{p}}(1)$
, it follows that (60) holds also unconditionally.
Since
![]() ${N_0({\mathcal T}^{\textbf{w},\circ}_{n})}/{n}\leqslant1$
, dominated convergence yields
${N_0({\mathcal T}^{\textbf{w},\circ}_{n})}/{n}\leqslant1$
, dominated convergence yields
and thus, by dominated convergence again,
The definition of
![]() $\widehat{{\mathcal T}}^{\textbf{w},\circ}_{n}$
by biasing means that for any bounded (or non-negative) function
$\widehat{{\mathcal T}}^{\textbf{w},\circ}_{n}$
by biasing means that for any bounded (or non-negative) function
![]() $f\,:\,\mathfrak{L}_n\to\mathbb R$
,
$f\,:\,\mathfrak{L}_n\to\mathbb R$
,
and thus, for any indicator function f,
 \begin{align}\bigl\lvert{{\mathbb E{}} f(\widehat{{\mathcal T}}^{\textbf{w},\circ}_{n})-{\mathbb E{}} f({\mathcal T}^{\textbf{w},\circ}_{n})}\bigr\rvert&=\Bigl\lvert{{\mathbb E{}} \Bigl[{f({\mathcal T}^{\textbf{w},\circ}_{n})\Bigl({\frac{{N_0({\mathcal T}^{\textbf{w},\circ}_{n})}}{{\mathbb E{}} N_0({\mathcal T}^{\textbf{w},\circ}_{n})}-1}\Bigr)}\Bigr]}\Bigr\rvert\notag\\&\leqslant{\mathbb E{}} \Bigl\lvert{\frac{{N_0({\mathcal T}^{\textbf{w},\circ}_{n})}}{{\mathbb E{}} N_0({\mathcal T}^{\textbf{w},\circ}_{n})}-1}\Bigr\rvert.\end{align}
\begin{align}\bigl\lvert{{\mathbb E{}} f(\widehat{{\mathcal T}}^{\textbf{w},\circ}_{n})-{\mathbb E{}} f({\mathcal T}^{\textbf{w},\circ}_{n})}\bigr\rvert&=\Bigl\lvert{{\mathbb E{}} \Bigl[{f({\mathcal T}^{\textbf{w},\circ}_{n})\Bigl({\frac{{N_0({\mathcal T}^{\textbf{w},\circ}_{n})}}{{\mathbb E{}} N_0({\mathcal T}^{\textbf{w},\circ}_{n})}-1}\Bigr)}\Bigr]}\Bigr\rvert\notag\\&\leqslant{\mathbb E{}} \Bigl\lvert{\frac{{N_0({\mathcal T}^{\textbf{w},\circ}_{n})}}{{\mathbb E{}} N_0({\mathcal T}^{\textbf{w},\circ}_{n})}-1}\Bigr\rvert.\end{align}
Hence, taking the supremum over all
![]() $f=\boldsymbol1_{A}$
,
$f=\boldsymbol1_{A}$
,
and the result follows by (63).
Lemma 8.2 implies that any result on convergence in probability or distribution for one of
![]() $\ {\widehat{{\mathcal T}}^{\textbf{w},\circ}_{n}}$
and
$\ {\widehat{{\mathcal T}}^{\textbf{w},\circ}_{n}}$
and
![]() ${\mathcal T}^{\textbf{w},\circ}_{n}$
also hold for the other.
${\mathcal T}^{\textbf{w},\circ}_{n}$
also hold for the other.
9. Profile of conditioned modified Galton–Watson trees
We will use the following extension of Theorem 1.2 to conditioned modified Galton–Watson trees.
Theorem 9.1. Let
![]() $L_n$
be the profile of a conditioned modified Galton–Watson tree
$L_n$
be the profile of a conditioned modified Galton–Watson tree
![]() ${\mathcal T}^{{{\textbf{p}},{\textbf{p}}^0}}_n$
of order n and assume that
${\mathcal T}^{{{\textbf{p}},{\textbf{p}}^0}}_n$
of order n and assume that
![]() $\mu({\textbf{p}})=1$
,
$\mu({\textbf{p}})=1$
,
![]() $\sigma^2({\textbf{p}})<\infty$
and
$\sigma^2({\textbf{p}})<\infty$
and
![]() $\mu({\textbf{p}}^0)<\infty$
. Then, as
$\mu({\textbf{p}}^0)<\infty$
. Then, as
![]() ${{n\to\infty}}$
,
${{n\to\infty}}$
,
in the space
![]() $C[0,\infty]$
, where
$C[0,\infty]$
, where
![]() $L_{{\textbf{e}}}$
is, as in Theorem 1.2, the local time of a standard Brownian excursion
$L_{{\textbf{e}}}$
is, as in Theorem 1.2, the local time of a standard Brownian excursion
![]() ${\textbf{e}}$
.
${\textbf{e}}$
.
Proof. Denote the branches of
![]() ${\mathcal T}^{{\textbf{p},\textbf{p}^0}}_n$
by
${\mathcal T}^{{\textbf{p},\textbf{p}^0}}_n$
by
![]() ${\mathcal T}_1,\dots,{\mathcal T}_{d(o)}$
and let
${\mathcal T}_1,\dots,{\mathcal T}_{d(o)}$
and let
![]() ${\mathcal T}_0$
be a single root. Then, regarding the branches as rooted trees, which means that their vertices have their depths shifted by 1 from the original tree,
${\mathcal T}_0$
be a single root. Then, regarding the branches as rooted trees, which means that their vertices have their depths shifted by 1 from the original tree,
 \begin{align}L_n(x)=\sum_{i=1}^{d(o)} L_{{\mathcal T}_i}(x-1)+L_{{\mathcal T}_0}(x).\end{align}
\begin{align}L_n(x)=\sum_{i=1}^{d(o)} L_{{\mathcal T}_i}(x-1)+L_{{\mathcal T}_0}(x).\end{align}
Let
![]() ${\mathcal T}_{(1)},\dots,{\mathcal T}_{({d(o)})}$
be the branches arranged in decreasing order. Lemma 4.3 shows that
${\mathcal T}_{(1)},\dots,{\mathcal T}_{({d(o)})}$
be the branches arranged in decreasing order. Lemma 4.3 shows that
![]() $|{\mathcal T}_{(1)}|=n-O_{\textrm{p}}(1)$
. Hence, (68) and the trivial estimate
$|{\mathcal T}_{(1)}|=n-O_{\textrm{p}}(1)$
. Hence, (68) and the trivial estimate
![]() $0\leqslant L_T(x)\leqslant |T|$
for any T and x yield
$0\leqslant L_T(x)\leqslant |T|$
for any T and x yield
 \begin{align}\bigl\lvert{L_n(x)-L_{{\mathcal T}_{(1)}}(x-1)}\bigr\rvert \leqslant\sum_{i=2}^{d(o)}|{\mathcal T}_{({i})}|+1=n-|{\mathcal T}_{(1)}|=O_{\textrm{p}}(1).\end{align}
\begin{align}\bigl\lvert{L_n(x)-L_{{\mathcal T}_{(1)}}(x-1)}\bigr\rvert \leqslant\sum_{i=2}^{d(o)}|{\mathcal T}_{({i})}|+1=n-|{\mathcal T}_{(1)}|=O_{\textrm{p}}(1).\end{align}
Furthermore, conditioned on
![]() $|{\mathcal T}_{(1)}|=n-\ell$
, for any fixed
$|{\mathcal T}_{(1)}|=n-\ell$
, for any fixed
![]() $\ell$
,
$\ell$
,
![]() ${\mathcal T}_{(1)}$
has the same distribution as
${\mathcal T}_{(1)}$
has the same distribution as
![]() ${\mathcal T}^{{\textbf{p}}}_{n-\ell}$
, and thus Theorem 1.2 shows that
${\mathcal T}^{{\textbf{p}}}_{n-\ell}$
, and thus Theorem 1.2 shows that
and it follows easily that, still conditioned,
Together with (69), this shows that for every fixed
![]() $\ell$
,
$\ell$
,
It follows that (72) holds also if we condition on
![]() $n-|{\mathcal T}_{(1)}|\leqslant K$
, for any fixed K, and then (67) follows easily from
$n-|{\mathcal T}_{(1)}|\leqslant K$
, for any fixed K, and then (67) follows easily from
![]() $n-|{\mathcal T}_{(1)}|=O_{\textrm{p}}(1)$
.
$n-|{\mathcal T}_{(1)}|=O_{\textrm{p}}(1)$
.
Recall that for conditioned Galton–Watson trees
![]() ${\mathcal T}^{{\textbf{p}}}_n$
with
${\mathcal T}^{{\textbf{p}}}_n$
with
![]() $\mu(\textbf{p})=1$
and
$\mu(\textbf{p})=1$
and
![]() $\sigma^2(\textbf{p})<\infty$
, the width divided by
$\sigma^2(\textbf{p})<\infty$
, the width divided by
![]() $\sqrt n$
converges in distribution: we have
$\sqrt n$
converges in distribution: we have
for some random variable W (not depending on
![]() $\textbf{p}$
). In fact, as noted by Drmota and Gittenberger [Reference Drmota and Gittenberger18], this is an immediate consequence of (13) and (1), with
$\textbf{p}$
). In fact, as noted by Drmota and Gittenberger [Reference Drmota and Gittenberger18], this is an immediate consequence of (13) and (1), with
It is also known that all moments converge, see [Reference Drmota and Gittenberger19] (assuming an exponential moment) and [Reference Addario-Berry, Devroye and Janson1] (in general).
The next theorem records that (73) extends to conditioned modified Galton–Watson trees, together with two partial results on moments.
Theorem 9.2. Consider a conditioned modified Galton–Watson tree
![]() ${\mathcal T}^{{{\textbf{p}},{\textbf{p}}^0}}_n$
where
${\mathcal T}^{{{\textbf{p}},{\textbf{p}}^0}}_n$
where
![]() $\mu({\textbf{p}})=1$
,
$\mu({\textbf{p}})=1$
,
![]() $\sigma^2({\textbf{p}})<\infty$
and
$\sigma^2({\textbf{p}})<\infty$
and
![]() $\sigma^2({\textbf{p}}^0)<\infty$
. Then, as
$\sigma^2({\textbf{p}}^0)<\infty$
. Then, as
![]() ${{n\to\infty}}$
,
${{n\to\infty}}$
,
Proof. First, (75) follows as in [Reference Drmota and Gittenberger18]:
![]() $f\to\sup f$
is a continuous functional on
$f\to\sup f$
is a continuous functional on
![]() $C[0,\infty]$
, and thus (75) follows from (67), (13) and (74).
$C[0,\infty]$
, and thus (75) follows from (67), (13) and (74).
We next prove (77). Denote the branches of
![]() ${\mathcal T}^{{\textbf{p},\textbf{p}^0}}_n$
by
${\mathcal T}^{{\textbf{p},\textbf{p}^0}}_n$
by
![]() ${\mathcal T}_1,\dots,{\mathcal T}_{d(o)}$
. Assume
${\mathcal T}_1,\dots,{\mathcal T}_{d(o)}$
. Assume
![]() $n>1$
, then the width is attained above the root, and we have, for every
$n>1$
, then the width is attained above the root, and we have, for every
![]() $i\leqslant d(o)$
,
$i\leqslant d(o)$
,
 \begin{align} W({\mathcal T}_i) \leqslant W({\mathcal T}^{{\textbf{p},\textbf{p}^0}}_n) \leqslant \sum_{i=1}^{d(o)}W({\mathcal T}_i).\end{align}
\begin{align} W({\mathcal T}_i) \leqslant W({\mathcal T}^{{\textbf{p},\textbf{p}^0}}_n) \leqslant \sum_{i=1}^{d(o)}W({\mathcal T}_i).\end{align}
Condition on d(o) and
![]() $|{\mathcal T}_1|,\dots,|{\mathcal T}_{d(o)}|$
as in Lemma 4.1. For a random variable X, denote its conditioned
$|{\mathcal T}_1|,\dots,|{\mathcal T}_{d(o)}|$
as in Lemma 4.1. For a random variable X, denote its conditioned
![]() $L^2$
norm by
$L^2$
norm by
By (78) and Minkowski’s inequality, we have
 \begin{align} \lVert{{W({\mathcal T}^{{\textbf{p},\textbf{p}^0}}_n)}}\rVert^{\prime}_2\leqslant \sum_{i=1}^{d(o)}\lVert{W({\mathcal T}_i)}\rVert^{\prime}_2.\end{align}
\begin{align} \lVert{{W({\mathcal T}^{{\textbf{p},\textbf{p}^0}}_n)}}\rVert^{\prime}_2\leqslant \sum_{i=1}^{d(o)}\lVert{W({\mathcal T}_i)}\rVert^{\prime}_2.\end{align}
Furthermore, by Lemma 4.1 and [Reference Addario-Berry, Devroye and Janson1, Corollary 1.3], if
![]() $|{\mathcal T}_i|=n_i$
,
$|{\mathcal T}_i|=n_i$
,
and thus
![]() $\lVert{{W({\mathcal T}_i)}}\rVert^{\prime}_2 \leqslant C n_i^{1/2} = C|{\mathcal T}_i|^{1/2}$
. Hence, by (80),
$\lVert{{W({\mathcal T}_i)}}\rVert^{\prime}_2 \leqslant C n_i^{1/2} = C|{\mathcal T}_i|^{1/2}$
. Hence, by (80),
 \begin{align} \lVert{{W({\mathcal T}^{{\textbf{p},\textbf{p}^0}}_n)}}\rVert^{\prime}_2\leqslant \sum_{i=1}^{d(o)} C |{\mathcal T}_i|^{1/2}\end{align}
\begin{align} \lVert{{W({\mathcal T}^{{\textbf{p},\textbf{p}^0}}_n)}}\rVert^{\prime}_2\leqslant \sum_{i=1}^{d(o)} C |{\mathcal T}_i|^{1/2}\end{align}
and thus, by the Cauchy–Schwarz inequality,
 \begin{align}&{{\mathbb E{}}\bigl[{ W({\mathcal T}^{{\textbf{p},\textbf{p}^0}}_n)^2\mid d(o),|{\mathcal T}_1|,\dots,|{\mathcal T}_{d(o)}|}\bigr]}=\bigl({ \lVert{{W({\mathcal T}^{{\textbf{p},\textbf{p}^0}}_n)}}\rVert^{\prime}_2}\bigr)^2\notag\\&\qquad\leqslant C\Bigl({ \sum_{i=1}^{d(o)} |{\mathcal T}_i|^{1/2}}\Bigr)^2\leqslant C d(o) \sum_{i=1}^{d(o)} |{\mathcal T}_i|\leqslant C d(o) n.\end{align}
\begin{align}&{{\mathbb E{}}\bigl[{ W({\mathcal T}^{{\textbf{p},\textbf{p}^0}}_n)^2\mid d(o),|{\mathcal T}_1|,\dots,|{\mathcal T}_{d(o)}|}\bigr]}=\bigl({ \lVert{{W({\mathcal T}^{{\textbf{p},\textbf{p}^0}}_n)}}\rVert^{\prime}_2}\bigr)^2\notag\\&\qquad\leqslant C\Bigl({ \sum_{i=1}^{d(o)} |{\mathcal T}_i|^{1/2}}\Bigr)^2\leqslant C d(o) \sum_{i=1}^{d(o)} |{\mathcal T}_i|\leqslant C d(o) n.\end{align}
Taking the expectation yields
Furthermore, (35) implies that for large n,
![]() ${\mathbb E{}}[{ d(o)}] \leqslant 2{\mathbb E{}}{ \widetilde D}$
, where
${\mathbb E{}}[{ d(o)}] \leqslant 2{\mathbb E{}}{ \widetilde D}$
, where
![]() ${\mathbb E{}}\widetilde D<\infty $
by Lemma 4.2. Thus,
${\mathbb E{}}\widetilde D<\infty $
by Lemma 4.2. Thus,
![]() ${\mathbb E{}} [{d(o)}]\leqslant C$
, and (84) yields
${\mathbb E{}} [{d(o)}]\leqslant C$
, and (84) yields
showing (77).
Finally, (77) implies that the variables on the left-hand side of (75) are uniformly integrable [Reference Gut26, Theorem 5.4.2], and thus (76) follows from (75).
![]() ${\mathbb E{}} W=\sqrt{\pi/2}$
is well known, see e.g. [Reference Biane, Pitman and Yor12].
${\mathbb E{}} W=\sqrt{\pi/2}$
is well known, see e.g. [Reference Biane, Pitman and Yor12].
Problem 9.3. We conjecture that under the assumptions of Theorem 9.2,
![]() ${\mathbb E{}}\bigl[{ W({\mathcal T}^{{\textbf{p},\textbf{p}^0}}_n)^r}\bigr]=O\bigl({n^{r/2}}\bigr)$
for any
${\mathbb E{}}\bigl[{ W({\mathcal T}^{{\textbf{p},\textbf{p}^0}}_n)^r}\bigr]=O\bigl({n^{r/2}}\bigr)$
for any
![]() $r>0$
, which implies convergence of all moments in (75), as shown for the case
$r>0$
, which implies convergence of all moments in (75), as shown for the case
![]() $\textbf{p}^0=\textbf{p}$
in [Reference Addario-Berry, Devroye and Janson1]. The proof above is easily generalized if
$\textbf{p}^0=\textbf{p}$
in [Reference Addario-Berry, Devroye and Janson1]. The proof above is easily generalized if
![]() ${\mathbb E{}} \widetilde D^{r/2}=O(1)$
, which is equivalent to
${\mathbb E{}} \widetilde D^{r/2}=O(1)$
, which is equivalent to
![]() $\sum_k k^{1+r/2}{p}^0_k<\infty$
, but we leave the general case as an open problem.
$\sum_k k^{1+r/2}{p}^0_k<\infty$
, but we leave the general case as an open problem.
Problem 9.4. Is
![]() $\sigma^2(\textbf{p}^0)<\infty$
really needed in Theorem 9.2?
$\sigma^2(\textbf{p}^0)<\infty$
really needed in Theorem 9.2?
10. Distance profile, first step
We now turn to distance profiles. We begin with a weak version of Theorem 1.4; recall the pseudometric
![]() $\textsf{d}$
defined in (20), and (21).
$\textsf{d}$
defined in (20), and (21).
Lemma 10.1. Consider a conditioned Galton–Watson tree
![]() ${\mathcal T}^{{{\textbf{p}}}}_n$
where
${\mathcal T}^{{{\textbf{p}}}}_n$
where
![]() $\mu({\textbf{p}})=1$
and
$\mu({\textbf{p}})=1$
and
![]() $\sigma^2=\sigma^2({\textbf{p}})<\infty$
. Then, as
$\sigma^2=\sigma^2({\textbf{p}})<\infty$
. Then, as
![]() ${{n\to\infty}}$
, for any continuous function with compact support
${{n\to\infty}}$
, for any continuous function with compact support
![]() $f\,:\,[0,\infty)\to\mathbb R$
,
$f\,:\,[0,\infty)\to\mathbb R$
,
Proof. The function f is bounded, and also uniformly continuous, i.e., its modulus of continuity
![]() $\omega(\delta;\,f)$
, defined in (9), satisfies
$\omega(\delta;\,f)$
, defined in (9), satisfies
![]() $\omega(\delta;\,f)\to0$
as
$\omega(\delta;\,f)\to0$
as
![]() $\delta\to0$
. Thus, for any rooted tree
$\delta\to0$
. Thus, for any rooted tree
![]() $T\in\mathfrak{T}_n$
, noting that
$T\in\mathfrak{T}_n$
, noting that
![]() $\Lambda_T(x)\leqslant n$
on
$\Lambda_T(x)\leqslant n$
on
![]() $[\!-\!1,0]$
and using the analogue of (11) for
$[\!-\!1,0]$
and using the analogue of (11) for
![]() $\Lambda$
,
$\Lambda$
,
 \begin{align}\hskip2em&\hskip-2em\int_0^\infty n^{-3/2} \Lambda_T\bigl({x n^{1/2}}\bigr)f(x) \,\textrm{d} x= n^{-2}\int_0^\infty \Lambda_T({x})f\bigl({n^{-1/2} x}\bigr) \,\textrm{d} x\notag\\&= n^{-2}\int_{-1}^\infty f\bigl({n^{-1/2} x}\bigr)\Lambda_T({x}) \,\textrm{d} x+O\bigl({n^{-1}}\bigr)\notag\\&= n^{-2}\sum_{i=0}^\infty \int_{i-1}^{i+1}f\bigl({n^{-1/2} x}\bigr)\Lambda_T(i)\tau(x-i) \,\textrm{d} x +O\bigl({n^{-1}}\bigr)\notag\\&= n^{-2}\sum_{i=0}^\infty f\bigl({n^{-1/2} i}\bigr)\Lambda_T(i)+ O\bigl({\omega(n^{-1/2};\,f)}\bigr)+O\bigl({n^{-1}}\bigr)\notag\\&= n^{-2}\sum_{v,w\in T} f\bigl({n^{-1/2}\textsf{d}(v,w)}\bigr)+ o(1),\end{align}
\begin{align}\hskip2em&\hskip-2em\int_0^\infty n^{-3/2} \Lambda_T\bigl({x n^{1/2}}\bigr)f(x) \,\textrm{d} x= n^{-2}\int_0^\infty \Lambda_T({x})f\bigl({n^{-1/2} x}\bigr) \,\textrm{d} x\notag\\&= n^{-2}\int_{-1}^\infty f\bigl({n^{-1/2} x}\bigr)\Lambda_T({x}) \,\textrm{d} x+O\bigl({n^{-1}}\bigr)\notag\\&= n^{-2}\sum_{i=0}^\infty \int_{i-1}^{i+1}f\bigl({n^{-1/2} x}\bigr)\Lambda_T(i)\tau(x-i) \,\textrm{d} x +O\bigl({n^{-1}}\bigr)\notag\\&= n^{-2}\sum_{i=0}^\infty f\bigl({n^{-1/2} i}\bigr)\Lambda_T(i)+ O\bigl({\omega(n^{-1/2};\,f)}\bigr)+O\bigl({n^{-1}}\bigr)\notag\\&= n^{-2}\sum_{v,w\in T} f\bigl({n^{-1/2}\textsf{d}(v,w)}\bigr)+ o(1),\end{align}
where (as throughout the proof) o(1) tends to 0 as
![]() ${{n\to\infty}}$
, uniformly in
${{n\to\infty}}$
, uniformly in
![]() $T\in\mathfrak{T}_n$
. Recall that the contour process
$T\in\mathfrak{T}_n$
. Recall that the contour process
![]() $C_T(x)$
of T is a continuous function
$C_T(x)$
of T is a continuous function
![]() $C_T\,:\,[0,2n-2]\to[0,\infty)$
that describes the distance from the root to a particle that travels with speed 1 on the ‘outside’ of the tree. (Equivalently, it performs a depth first walk at integer times
$C_T\,:\,[0,2n-2]\to[0,\infty)$
that describes the distance from the root to a particle that travels with speed 1 on the ‘outside’ of the tree. (Equivalently, it performs a depth first walk at integer times
![]() $0,1,\dots,2n-2$
.) For each vertex
$0,1,\dots,2n-2$
.) For each vertex
![]() $v\neq o$
, the particle travels through the edge leading from v towards the root during two time intervals of unit length (once in each direction). Thus, as is well known,
$v\neq o$
, the particle travels through the edge leading from v towards the root during two time intervals of unit length (once in each direction). Thus, as is well known,
 \begin{align} \int_0^{2n-2} f\bigl({n^{-1/2} C_T(x)}\bigr)\,\textrm{d} x= 2\sum_{v\neq o} f\bigl({n^{-1/2} \textsf{d}(v,o)}\bigr)+O\bigl({n\omega(n^{-1/2};\, f)}\bigr).\end{align}
\begin{align} \int_0^{2n-2} f\bigl({n^{-1/2} C_T(x)}\bigr)\,\textrm{d} x= 2\sum_{v\neq o} f\bigl({n^{-1/2} \textsf{d}(v,o)}\bigr)+O\bigl({n\omega(n^{-1/2};\, f)}\bigr).\end{align}
We will use a bivariate version of this. It is also well known that if v(i) is the vertex visited by the particle at time i, then, for any integers
![]() $i,j\in[0,2n-2]$
,
$i,j\in[0,2n-2]$
,
where the first
![]() $\textsf{d}$
is the graph distance in T, and the second is the pseudometric defined by (20) (now on the interval
$\textsf{d}$
is the graph distance in T, and the second is the pseudometric defined by (20) (now on the interval
![]() $[0,2n-2]$
). Hence, the argument yielding (88) also yields
$[0,2n-2]$
). Hence, the argument yielding (88) also yields
 \begin{align}\int_0^{2n-2}\int_0^{2n-2}f\bigl({n^{-1/2}\textsf{d}(x,y;\,C_T)}\bigr)\,\textrm{d} x\,\textrm{d} y =4 \sum_{v,w\neq o} f\bigl({n^{-1/2}\textsf{d}(v,w)}\bigr) + O\bigl({n^2\omega(n^{-1/2};\,f)}\bigr).\end{align}
\begin{align}\int_0^{2n-2}\int_0^{2n-2}f\bigl({n^{-1/2}\textsf{d}(x,y;\,C_T)}\bigr)\,\textrm{d} x\,\textrm{d} y =4 \sum_{v,w\neq o} f\bigl({n^{-1/2}\textsf{d}(v,w)}\bigr) + O\bigl({n^2\omega(n^{-1/2};\,f)}\bigr).\end{align}
We use the standard rescaling of the contour process
and note that for any
![]() $g\,:\,[0,1] \rightarrow [0, \infty)$
with
$g\,:\,[0,1] \rightarrow [0, \infty)$
with
![]() $g(0) = g(1) = 0$
and
$g(0) = g(1) = 0$
and
![]() $c>0$
,
$c>0$
,
Thus, by (90) and a change of variables,
 \begin{align}\hskip4em&\hskip-4em\int_0^{1}\int_0^{1}f\bigl({\textsf{d}(s,t;\,\widetilde C_T)}\bigr)\,\textrm{d} s\,\textrm{d} t\notag\\&=\frac{1}{(2n-2)^2}\int_0^{2n-2}\int_0^{2n-2}f\bigl({n^{-1/2}\textsf{d}(x,y;\,C_T)}\bigr)\,\textrm{d} x\,\textrm{d} y\notag\\&=\frac{1}{(n-1)^2} \sum_{v,w\neq o} f\bigl({n^{-1/2}\textsf{d}(v,w)}\bigr)+ O\bigl({\omega(n^{-1/2};\,f)}\bigr).\notag\\&=\frac{1}{n^2} \sum_{v,w\neq o} f\bigl({n^{-1/2}\textsf{d}(v,w)}\bigr) +o(1).\end{align}
\begin{align}\hskip4em&\hskip-4em\int_0^{1}\int_0^{1}f\bigl({\textsf{d}(s,t;\,\widetilde C_T)}\bigr)\,\textrm{d} s\,\textrm{d} t\notag\\&=\frac{1}{(2n-2)^2}\int_0^{2n-2}\int_0^{2n-2}f\bigl({n^{-1/2}\textsf{d}(x,y;\,C_T)}\bigr)\,\textrm{d} x\,\textrm{d} y\notag\\&=\frac{1}{(n-1)^2} \sum_{v,w\neq o} f\bigl({n^{-1/2}\textsf{d}(v,w)}\bigr)+ O\bigl({\omega(n^{-1/2};\,f)}\bigr).\notag\\&=\frac{1}{n^2} \sum_{v,w\neq o} f\bigl({n^{-1/2}\textsf{d}(v,w)}\bigr) +o(1).\end{align}
Combining (87) and (93), we find
We apply this to
![]() $T={\mathcal T}^{{\textbf{p}}}_n$
and use the result by Aldous [Reference Aldous3, Reference Aldous4],
$T={\mathcal T}^{{\textbf{p}}}_n$
and use the result by Aldous [Reference Aldous3, Reference Aldous4],
The functional
![]() $g\to\iint f\bigl({d(s,t;\,g)}\bigr)\,\textrm{d} s\,\textrm{d} t$
is continuous on
$g\to\iint f\bigl({d(s,t;\,g)}\bigr)\,\textrm{d} s\,\textrm{d} t$
is continuous on
![]() $C{[0,1]}$
, and the result (86) follows from (94) and (95) by the continuous mapping theorem, using also (92).
$C{[0,1]}$
, and the result (86) follows from (94) and (95) by the continuous mapping theorem, using also (92).
11. Distance profile of unrooted trees
We continue with the distance profile, now turning to unrooted simply generated trees for a while. Throughout this section, we assume that
![]() $\textbf{w}$
is a weight sequence and that
$\textbf{w}$
is a weight sequence and that
![]() $\boldsymbol{\phi}$
and
$\boldsymbol{\phi}$
and
![]() $\boldsymbol{\phi}^0$
are the weight sequences given by (49) and (50). We assume that the exponential generating function of
$\boldsymbol{\phi}^0$
are the weight sequences given by (49) and (50). We assume that the exponential generating function of
![]() $\textbf{w}$
has positive radius of convergence; this means that the generating function
$\textbf{w}$
has positive radius of convergence; this means that the generating function
![]() $\Phi(z)$
in (29) has positive radius of convergence, which in turn implies that there exists a probability weight sequence
$\Phi(z)$
in (29) has positive radius of convergence, which in turn implies that there exists a probability weight sequence
![]() $\textbf{p}$
equivalent to
$\textbf{p}$
equivalent to
![]() $\boldsymbol{\phi}$
. We assume furthermore that it is possible to choose
$\boldsymbol{\phi}$
. We assume furthermore that it is possible to choose
![]() $\textbf{p}$
such that
$\textbf{p}$
such that
![]() $\mu(\textbf{p})=1$
;
$\mu(\textbf{p})=1$
;
![]() $\textbf{p}$
will denote this choice. (For algebraic conditions on
$\textbf{p}$
will denote this choice. (For algebraic conditions on
![]() $\Phi$
for such a
$\Phi$
for such a
![]() $\textbf{p}$
to exist, see e.g. [Reference Janson30].)
$\textbf{p}$
to exist, see e.g. [Reference Janson30].)
We note that by (49)–(50),
![]() $\phi^0_k\leqslant\phi_{k-1}$
,
$\phi^0_k\leqslant\phi_{k-1}$
,
![]() $k\geqslant1$
. Hence, if
$k\geqslant1$
. Hence, if
![]() $p_k=ab^k\phi_k$
, then
$p_k=ab^k\phi_k$
, then
![]() $\sum_k b^k\phi^0_k<\infty$
, and it is possible to find
$\sum_k b^k\phi^0_k<\infty$
, and it is possible to find
![]() $a_0>0$
such that
$a_0>0$
such that
![]() $\textbf{p}^0\,:\!=\,\boldsymbol{\phi}^{0\prime}$
given by (32) also is a probability sequence; hence
$\textbf{p}^0\,:\!=\,\boldsymbol{\phi}^{0\prime}$
given by (32) also is a probability sequence; hence
![]() ${\mathcal T}^{{\boldsymbol{\phi},\boldsymbol{\phi}^0}}_n={\mathcal T}^{{\textbf{p},\textbf{p}^0}}_n$
is a modified Galton–Watson tree. Furthermore,
${\mathcal T}^{{\boldsymbol{\phi},\boldsymbol{\phi}^0}}_n={\mathcal T}^{{\textbf{p},\textbf{p}^0}}_n$
is a modified Galton–Watson tree. Furthermore,
![]() ${p}^0_k\leqslant (a_0/a)p_k$
, and thus if
${p}^0_k\leqslant (a_0/a)p_k$
, and thus if
![]() $\sigma^2(\textbf{p})<\infty$
, then
$\sigma^2(\textbf{p})<\infty$
, then
![]() $\sigma^2(\textbf{p}^0)<\infty$
.
$\sigma^2(\textbf{p}^0)<\infty$
.
We begin with an unrooted version of Lemma 10.1.
Lemma 11.1. Let
![]() ${\textbf{w}}$
,
${\textbf{w}}$
,
![]() $\boldsymbol{\phi}$
and
$\boldsymbol{\phi}$
and
![]() ${\textbf{p}}$
be as above and assume
${\textbf{p}}$
be as above and assume
![]() $\sigma^2\,:\!=\,\sigma^2({\textbf{p}})<\infty$
. Let
$\sigma^2\,:\!=\,\sigma^2({\textbf{p}})<\infty$
. Let
![]() $\Lambda_n$
be the distance profile of the unrooted simply generated tree
$\Lambda_n$
be the distance profile of the unrooted simply generated tree
![]() ${\mathcal T}^{{\textbf{w}},\circ}_{n}$
. Then, as
${\mathcal T}^{{\textbf{w}},\circ}_{n}$
. Then, as
![]() ${{n\to\infty}}$
, for any continuous function with compact support
${{n\to\infty}}$
, for any continuous function with compact support
![]() $f\,:\,[0,\infty)\to\mathbb R$
,
$f\,:\,[0,\infty)\to\mathbb R$
,
Proof. Consider the leaf-biased random tree
![]() $\widehat{{\mathcal T}}^{\textbf{w},\circ}_{n}$
defined in Section 8. By Lemma 8.2, we may assume
$\widehat{{\mathcal T}}^{\textbf{w},\circ}_{n}$
defined in Section 8. By Lemma 8.2, we may assume
![]() ${\mathbb P{}}(\widehat{{\mathcal T}}^{\textbf{w},\circ}_{n}\neq{\mathcal T}^{\textbf{w},\circ}_{n})\to0$
and thus it suffices to show (96) with
${\mathbb P{}}(\widehat{{\mathcal T}}^{\textbf{w},\circ}_{n}\neq{\mathcal T}^{\textbf{w},\circ}_{n})\to0$
and thus it suffices to show (96) with
![]() $\Lambda_{\widehat{{\mathcal T}}^{\textbf{w},\circ}_{n}}$
instead of
$\Lambda_{\widehat{{\mathcal T}}^{\textbf{w},\circ}_{n}}$
instead of
![]() $\Lambda_n$
. If
$\Lambda_n$
. If
![]() ${\mathcal T}_{n,+}$
denotes the unique branch of
${\mathcal T}_{n,+}$
denotes the unique branch of
![]() $\widehat{{\mathcal T}}^{\textbf{w},\circ}_{n}$
, then, trivially,
$\widehat{{\mathcal T}}^{\textbf{w},\circ}_{n}$
, then, trivially,
and thus we may further reduce and replace
![]() $\Lambda_n$
in (96) by
$\Lambda_n$
in (96) by
![]() $\Lambda_{{\mathcal T}_{n,+}}$
. As shown in Section 8,
$\Lambda_{{\mathcal T}_{n,+}}$
. As shown in Section 8,
![]() ${\mathcal T}_{n,+}\overset{\textrm{d}}{=}{\mathcal T}^{{\boldsymbol{\phi}}}_{n-1}={\mathcal T}^{{\textbf{p}}}_{n-1}$
, and the result now follows from Lemma 10.1, replacing n there by
${\mathcal T}_{n,+}\overset{\textrm{d}}{=}{\mathcal T}^{{\boldsymbol{\phi}}}_{n-1}={\mathcal T}^{{\textbf{p}}}_{n-1}$
, and the result now follows from Lemma 10.1, replacing n there by
![]() $n-1$
and x by
$n-1$
and x by
![]() $x=(n/(n-1))^{1/2} x$
, noting that
$x=(n/(n-1))^{1/2} x$
, noting that
![]() $\sup_x|f(x)-f\bigl({(n/(n-1))^{1/2} x}\bigr)|\to0$
as
$\sup_x|f(x)-f\bigl({(n/(n-1))^{1/2} x}\bigr)|\to0$
as
![]() ${{n\to\infty}}$
.
${{n\to\infty}}$
.
Theorem 11.2. Let
![]() ${\textbf{w}}$
,
${\textbf{w}}$
,
![]() $\boldsymbol{\phi}$
and
$\boldsymbol{\phi}$
and
![]() ${\textbf{p}}$
be as above, and assume
${\textbf{p}}$
be as above, and assume
![]() $\sigma^2\,:\!=\,\sigma^2({\textbf{p}})<\infty$
. Let
$\sigma^2\,:\!=\,\sigma^2({\textbf{p}})<\infty$
. Let
![]() $\Lambda_n$
be the distance profile of the unrooted simply generated tree
$\Lambda_n$
be the distance profile of the unrooted simply generated tree
![]() ${\mathcal T}^{{\textbf{w}},\circ}_{n}$
. Then, as
${\mathcal T}^{{\textbf{w}},\circ}_{n}$
. Then, as
![]() ${{n\to\infty}}$
,
${{n\to\infty}}$
,
in the space
![]() $C[0,\infty]$
, where
$C[0,\infty]$
, where
![]() $\Lambda_{{\textbf{e}}}(x)$
is as in Theorem 1.4.
$\Lambda_{{\textbf{e}}}(x)$
is as in Theorem 1.4.
Proof. Let
Regard
![]() $Y_n$
as a random element of
$Y_n$
as a random element of
![]() $C[0,\infty]$
. Define also the mapping
$C[0,\infty]$
. Define also the mapping
![]() $\psi\,:\,C[0,\infty]\to\mathcal M([0,\infty))$
, the space of all locally finite Borel measures on
$\psi\,:\,C[0,\infty]\to\mathcal M([0,\infty))$
, the space of all locally finite Borel measures on
![]() $[0,\infty)$
, defined by
$[0,\infty)$
, defined by
![]() $\psi(h)\,:\!=\,h(x)\,\textrm{d} x$
; i.e., for
$\psi(h)\,:\!=\,h(x)\,\textrm{d} x$
; i.e., for
![]() $h\in C[0,\infty]$
and
$h\in C[0,\infty]$
and
![]() $f\in C[0,\infty)$
with compact support,
$f\in C[0,\infty)$
with compact support,
In other word,
![]() $\psi(h)$
has density h.
$\psi(h)$
has density h.
We give
![]() $\mathcal M([0,\infty))$
the vague topology, i.e.,
$\mathcal M([0,\infty))$
the vague topology, i.e.,
![]() $\nu_n\to\nu$
in
$\nu_n\to\nu$
in
![]() $\mathcal M([0,\infty))$
if
$\mathcal M([0,\infty))$
if
![]() $\int f\,\textrm{d}\nu_n\to\int f\,\textrm{d}\nu$
for every
$\int f\,\textrm{d}\nu_n\to\int f\,\textrm{d}\nu$
for every
![]() $f\in C[0,\infty)$
with compact support, and note that
$f\in C[0,\infty)$
with compact support, and note that
![]() $\mathcal M([0,\infty))$
is a Polish space, see e.g. [Reference Kallenberg32, Theorem A2.3]. Clearly, the separable Banach space
$\mathcal M([0,\infty))$
is a Polish space, see e.g. [Reference Kallenberg32, Theorem A2.3]. Clearly, the separable Banach space
![]() $C[0,\infty]$
is also a Polish space. (Recall that a Polish space has a topology that can be defined by a complete separable metric.) It follows from the definition (100) that
$C[0,\infty]$
is also a Polish space. (Recall that a Polish space has a topology that can be defined by a complete separable metric.) It follows from the definition (100) that
![]() $\psi$
is continuous
$\psi$
is continuous
![]() $C[0,\infty]\to\mathcal M([0,\infty))$
. Furthermore,
$C[0,\infty]\to\mathcal M([0,\infty))$
. Furthermore,
![]() $\psi$
is injective, since the density of a measure is a.e. uniquely determined.
$\psi$
is injective, since the density of a measure is a.e. uniquely determined.
We will use the alternative method of proof in [Reference Drmota17, p. 123–125], and show the following two properties:
Claim 1. The sequence
![]() $Y_n$
is tight in
$Y_n$
is tight in
![]() $C[0,\infty]$
.
$C[0,\infty]$
.
Claim 2. The sequence of random measures
![]() $\psi(Y_n)$
converges in distribution in
$\psi(Y_n)$
converges in distribution in
![]() $\mathcal M([0,\infty))$
to some random measure
$\mathcal M([0,\infty))$
to some random measure
![]() $\zeta$
.
$\zeta$
.
It then follows from [Reference Bousquet-Mélou and Janson14, Lemma 7.1] (see also [Reference Drmota17, Theorem 4.17]) that
for some random
![]() $Z\in C[0,\infty]$
such that
$Z\in C[0,\infty]$
such that
It will then be easy to complete the proof.
Proof of Claim 1: For
![]() $i=1,\dots,n$
, let
$i=1,\dots,n$
, let
![]() ${\mathcal T}(i)$
be
${\mathcal T}(i)$
be
![]() ${\mathcal T}^{\textbf{w},\circ}_{n}$
rooted at i. By symmetry, all
${\mathcal T}^{\textbf{w},\circ}_{n}$
rooted at i. By symmetry, all
![]() ${\mathcal T}(i)$
have the same distribution; moreover, they equal in distribution
${\mathcal T}(i)$
have the same distribution; moreover, they equal in distribution
![]() $\widehat{{\mathcal T}}^{\textbf{w},\bullet}_{n}$
defined in Section 6 (which has a random root). Hence, if we order each
$\widehat{{\mathcal T}}^{\textbf{w},\bullet}_{n}$
defined in Section 6 (which has a random root). Hence, if we order each
![]() ${\mathcal T}(i)$
randomly, we have by Section 6
${\mathcal T}(i)$
randomly, we have by Section 6
By (16),
Since the sequence
![]() $n^{-1/2} L_{{\mathcal T}^{{\textbf{p},\textbf{p}^0}}_n}\bigl({xn^{1/2}}\bigr)$
converges in
$n^{-1/2} L_{{\mathcal T}^{{\textbf{p},\textbf{p}^0}}_n}\bigl({xn^{1/2}}\bigr)$
converges in
![]() $C[0,\infty]$
by Theorem 9.1, it is tight in
$C[0,\infty]$
by Theorem 9.1, it is tight in
![]() $C[0,\infty]$
. Furthermore,
$C[0,\infty]$
. Furthermore,
which are uniformly integrable by (77) in Theorem 9.2. Hence, by Lemma A.2 (which we state and prove in Appendix A) and Remark A.3, (104) and (103) imply that the sequence
![]() $Y_n$
is tight in
$Y_n$
is tight in
![]() $C[0,\infty]$
, proving Claim 1.
$C[0,\infty]$
, proving Claim 1.
Proof of Claim 2: Let
![]() $f\in C[0,\infty)$
have compact support. Then, Lemma 11.1 shows that
$f\in C[0,\infty)$
have compact support. Then, Lemma 11.1 shows that
 \begin{align} \int_0^\infty f(x)\,\textrm{d}\psi(Y_n)&=\int_0^\infty f(x)Y_n(x)\,\textrm{d} x\overset{\textrm{d}}{\longrightarrow}\int_0^1\int_0^1 f\Bigl({\frac{2}{\sigma}\textsf{d}\bigl({s,t;\,\textbf{e}}\bigr)}\Bigr)\,\textrm{d} s\,\textrm{d} t\notag\\&=\int_0^\infty f(x)\,\textrm{d}\zeta(x),\end{align}
\begin{align} \int_0^\infty f(x)\,\textrm{d}\psi(Y_n)&=\int_0^\infty f(x)Y_n(x)\,\textrm{d} x\overset{\textrm{d}}{\longrightarrow}\int_0^1\int_0^1 f\Bigl({\frac{2}{\sigma}\textsf{d}\bigl({s,t;\,\textbf{e}}\bigr)}\Bigr)\,\textrm{d} s\,\textrm{d} t\notag\\&=\int_0^\infty f(x)\,\textrm{d}\zeta(x),\end{align}
where
![]() $\zeta$
is the (random) probability measure on
$\zeta$
is the (random) probability measure on
![]() $[0,\infty)$
defined as the push-forward of Lebesgue measure on
$[0,\infty)$
defined as the push-forward of Lebesgue measure on
![]() ${[0,1]}\times{[0,1]}$
by the map
${[0,1]}\times{[0,1]}$
by the map
![]() $(s,t)\to(2/\sigma)\textsf{d}(s,t;\,\textbf{e})$
; in other words,
$(s,t)\to(2/\sigma)\textsf{d}(s,t;\,\textbf{e})$
; in other words,
![]() $\zeta$
is the conditional distribution, given
$\zeta$
is the conditional distribution, given
![]() $\textbf{e}$
, of
$\textbf{e}$
, of
![]() $(2/\sigma)\textsf{d}(U_1,U_2;\,\textbf{e})$
where
$(2/\sigma)\textsf{d}(U_1,U_2;\,\textbf{e})$
where
![]() $U_1$
and
$U_1$
and
![]() $U_2$
are independent uniform
$U_2$
are independent uniform
![]() $U{[0,1]}$
random variables. This convergence in distribution for each f with compact support is equivalent to convergence in
$U{[0,1]}$
random variables. This convergence in distribution for each f with compact support is equivalent to convergence in
![]() $\mathcal M([0,\infty))$
, see [Reference Kallenberg32, Theorem 16.16]. Thus,
$\mathcal M([0,\infty))$
, see [Reference Kallenberg32, Theorem 16.16]. Thus,
![]() $\psi(Y_n)\overset{\textrm{d}}{\longrightarrow} \zeta$
in
$\psi(Y_n)\overset{\textrm{d}}{\longrightarrow} \zeta$
in
![]() $\mathcal M([0,\infty))$
, proving Claim 2.
$\mathcal M([0,\infty))$
, proving Claim 2.
As said above, the claims imply (101)–(102). Thus, by the definition of
![]() $\zeta$
above, see (106), for any bounded measurable
$\zeta$
above, see (106), for any bounded measurable
![]() $f\,:\,[0,\infty)\to\mathbb R$
,
$f\,:\,[0,\infty)\to\mathbb R$
,
 \begin{align}\int_0^\infty f(x) Z(x)\,\textrm{d} x&=\int_0^\infty f(x)\,\textrm{d}\psi(Z)=\int_0^\infty f(x)\,\textrm{d}\zeta(x)\notag\\&=\int_0^1\int_0^1 f\Bigl({\frac{2}{\sigma}\textsf{d}\bigl({s,t;\,\textbf{e}}\bigr)}\Bigr)\,\textrm{d} s\,\textrm{d} t.\end{align}
\begin{align}\int_0^\infty f(x) Z(x)\,\textrm{d} x&=\int_0^\infty f(x)\,\textrm{d}\psi(Z)=\int_0^\infty f(x)\,\textrm{d}\zeta(x)\notag\\&=\int_0^1\int_0^1 f\Bigl({\frac{2}{\sigma}\textsf{d}\bigl({s,t;\,\textbf{e}}\bigr)}\Bigr)\,\textrm{d} s\,\textrm{d} t.\end{align}
Define
Then, (101) is the same as (98). Furthermore, replacing f(x) by
![]() $f(\sigma x/2)$
in (107) yields after a simple change of variables (21) and thus (4). (In particular,
$f(\sigma x/2)$
in (107) yields after a simple change of variables (21) and thus (4). (In particular,
![]() $\Lambda_\textbf{e}$
does not depend on the weight sequence
$\Lambda_\textbf{e}$
does not depend on the weight sequence
![]() $\textbf{w}$
.)
$\textbf{w}$
.)
12. Distance profile of rooted trees
Finally, we can prove Theorem 1.4 as a simple consequence of the corresponding result Theorem 11.2 for unrooted trees.
Proof of Theorem 1.4. Let
![]() $\boldsymbol{\phi}=\textbf{p}$
, and use (49) to define the weight sequence
$\boldsymbol{\phi}=\textbf{p}$
, and use (49) to define the weight sequence
![]() $\textbf{w}$
. Then, Theorem 11.2 applies to
$\textbf{w}$
. Then, Theorem 11.2 applies to
![]() ${\mathcal T}^{\textbf{w},\circ}_{n}$
. Consider, as in the proof of Lemma 11.1, the leaf-biased unrooted random tree
${\mathcal T}^{\textbf{w},\circ}_{n}$
. Consider, as in the proof of Lemma 11.1, the leaf-biased unrooted random tree
![]() $\widehat{{\mathcal T}}^{\textbf{w},\circ}_{n}$
. By Lemma 8.2, Theorem 11.2 holds also for
$\widehat{{\mathcal T}}^{\textbf{w},\circ}_{n}$
. By Lemma 8.2, Theorem 11.2 holds also for
![]() $\widehat{{\mathcal T}}^{\textbf{w},\circ}_{n}$
.
$\widehat{{\mathcal T}}^{\textbf{w},\circ}_{n}$
.
Let again
![]() ${\mathcal T}_{n,+}\overset{\textrm{d}}{=} {\mathcal T}^{{\boldsymbol{\phi}}}_{n-1}={\mathcal T}^{{\textbf{p}}}_{n-1}$
denote the unique branch of
${\mathcal T}_{n,+}\overset{\textrm{d}}{=} {\mathcal T}^{{\boldsymbol{\phi}}}_{n-1}={\mathcal T}^{{\textbf{p}}}_{n-1}$
denote the unique branch of
![]() $\widehat{{\mathcal T}}^{\textbf{w},\circ}_{n}$
. By (97), Theorem 11.2 holds also for
$\widehat{{\mathcal T}}^{\textbf{w},\circ}_{n}$
. By (97), Theorem 11.2 holds also for
![]() ${\mathcal T}_{n,+}$
and thus for
${\mathcal T}_{n,+}$
and thus for
![]() ${\mathcal T}^{{\textbf{p}}}_{n-1}$
. Replace n by
${\mathcal T}^{{\textbf{p}}}_{n-1}$
. Replace n by
![]() $n+1$
, then a change of variables shows that Theorem 11.2 holds for
$n+1$
, then a change of variables shows that Theorem 11.2 holds for
![]() ${\mathcal T}^{{\textbf{p}}}_n$
too, which is Theorem 1.4.
${\mathcal T}^{{\textbf{p}}}_n$
too, which is Theorem 1.4.
As part of the proof, we have shown the corresponding result Theorem 11.2 for unrooted trees. The result also extends easily to conditioned modified Galton–Watson trees, using the method by Marckert and Panholzer [Reference Marckert and Panholzer41] and Kortchemski and Marzouk [Reference Kortchemski and Marzouk38].
Theorem 12.1. Let
![]() $\Lambda_n$
be the distance profile of a conditioned modified Galton–Watson tree
$\Lambda_n$
be the distance profile of a conditioned modified Galton–Watson tree
![]() ${\mathcal T}^{{\textbf{p},\textbf{p}^0}}_n$
of order n and assume that
${\mathcal T}^{{\textbf{p},\textbf{p}^0}}_n$
of order n and assume that
![]() $\mu(\textbf{p})=1$
,
$\mu(\textbf{p})=1$
,
![]() $\sigma^2(\textbf{p})<\infty$
and
$\sigma^2(\textbf{p})<\infty$
and
![]() $\mu(\textbf{p}^0)<\infty$
. Then, (3) holds as
$\mu(\textbf{p}^0)<\infty$
. Then, (3) holds as
![]() ${{n\to\infty}}$
.
${{n\to\infty}}$
.
Proof. This is a simple consequence of Theorem 1.4 and Lemma 4.3. It follows from (42) that
and thus (3) for
![]() ${\mathcal T}^{{\textbf{p},\textbf{p}^0}}_n$
follows from the same result for
${\mathcal T}^{{\textbf{p},\textbf{p}^0}}_n$
follows from the same result for
![]() ${\mathcal T}_{n,(1)}$
, which follows from (42) and Theorem 1.4 by conditioning on
${\mathcal T}_{n,(1)}$
, which follows from (42) and Theorem 1.4 by conditioning on
![]() $|{\mathcal T}_{n,(1)}|$
. We omit the details.
$|{\mathcal T}_{n,(1)}|$
. We omit the details.
13. Wiener index
Recall that the Wiener index of a tree T is defined as
where
![]() $\textsf{d}$
is the graph distance in T. Thus,
$\textsf{d}$
is the graph distance in T. Thus,
Since the integrand x in (111) is unbounded, convergence of the Wiener index does not follow immediately from convergence of the profile, but only a simple extra truncation argument is needed. For a conditioned Galton–Watson tree
![]() ${\mathcal T}^{{\textbf{p}}}_n$
, with
${\mathcal T}^{{\textbf{p}}}_n$
, with
![]() $\mu(\textbf{p})=1$
and
$\mu(\textbf{p})=1$
and
![]() $\sigma^2(\textbf{p})<\infty$
, convergence is more easily proved directly from Aldous’s result (95) [Reference Aldous3, Reference Aldous4], see [Reference Janson28], but as an application of the results above, we show the corresponding result for unrooted trees.
$\sigma^2(\textbf{p})<\infty$
, convergence is more easily proved directly from Aldous’s result (95) [Reference Aldous3, Reference Aldous4], see [Reference Janson28], but as an application of the results above, we show the corresponding result for unrooted trees.
Theorem 13.1. Let
![]() ${\textbf{w}}$
and
${\textbf{w}}$
and
![]() ${\textbf{p}}$
be as in Theorem 11.2. Then
${\textbf{p}}$
be as in Theorem 11.2. Then
Proof. Let
![]() $T\in\mathfrak{T}_n$
, and define a modified version by
$T\in\mathfrak{T}_n$
, and define a modified version by
using (111) and noting that
![]() $\Lambda_T(x)\leqslant n$
for
$\Lambda_T(x)\leqslant n$
for
![]() $x\in[\!-1,0]$
. It suffices to prove (112) for
$x\in[\!-1,0]$
. It suffices to prove (112) for
![]() ${Wie}'({\mathcal T}^{\textbf{w},\circ}_{n})$
. By (113),
${Wie}'({\mathcal T}^{\textbf{w},\circ}_{n})$
. By (113),
Define a truncated version by, for
![]() $m \geq 0$
,
$m \geq 0$
,
Then, since the support of
![]() $\Lambda_T$
is
$\Lambda_T$
is
![]() $[-1,\textrm{diam}(T)+1]$
,
$[-1,\textrm{diam}(T)+1]$
,
Since
![]() $\textrm{diam}({\mathcal T}^{\textbf{w},\circ}_{n}) = O_{\textrm{p}}(n^{1/2})$
, as an easy consequence of any of the constructions in Sections 6–8 and known results on the height of rooted Galton–Watson trees, see e.g. [Reference Aldous3, Reference Kolchin36] or [Reference Addario-Berry, Devroye and Janson1, Theorem 1.2], it follows that
$\textrm{diam}({\mathcal T}^{\textbf{w},\circ}_{n}) = O_{\textrm{p}}(n^{1/2})$
, as an easy consequence of any of the constructions in Sections 6–8 and known results on the height of rooted Galton–Watson trees, see e.g. [Reference Aldous3, Reference Kolchin36] or [Reference Addario-Berry, Devroye and Janson1, Theorem 1.2], it follows that
Furthermore, for each fixed m, (115) and Theorem 11.2 imply, as
![]() ${{n\to\infty}}$
,
${{n\to\infty}}$
,
 \begin{align}{n^{-5/2}}\textrm{Wie}_m({\mathcal T}^{\textbf{w},\circ}_{n})&\overset{\textrm{d}}{\longrightarrow}\frac{1}2\int_0^\infty (x\land m)\frac{\sigma}2\Lambda_\textbf{e}\Bigl({\frac{\sigma}2 x}\Bigr)\,\textrm{d} x\notag\\&=\frac{1}\sigma\int_0^\infty \bigl({x\land \frac{\sigma m}2}\bigr)\Lambda_\textbf{e}({x})\,\textrm{d} x.\end{align}
\begin{align}{n^{-5/2}}\textrm{Wie}_m({\mathcal T}^{\textbf{w},\circ}_{n})&\overset{\textrm{d}}{\longrightarrow}\frac{1}2\int_0^\infty (x\land m)\frac{\sigma}2\Lambda_\textbf{e}\Bigl({\frac{\sigma}2 x}\Bigr)\,\textrm{d} x\notag\\&=\frac{1}\sigma\int_0^\infty \bigl({x\land \frac{\sigma m}2}\bigr)\Lambda_\textbf{e}({x})\,\textrm{d} x.\end{align}
The convergence in (112) follows by (117) and (118), see [11, Theorem 4.2]. The equality in (112) holds by (21).
Of course, the limit in (112) agrees with the limit in [Reference Janson28] for the rooted case.
14. Moments of the distance profile
In this section, we prove the following estimates on moments of the distance profile for a conditioned Galton–Watson tree; we use again the simplified notation
![]() $L_n$
and
$L_n$
and
![]() $\Lambda_n$
for the profile and distance profile as in Theorems 1.2 and 1.4. Throughout the section, C and c denote some positive constants that may depend on the offspring distribution
$\Lambda_n$
for the profile and distance profile as in Theorems 1.2 and 1.4. Throughout the section, C and c denote some positive constants that may depend on the offspring distribution
![]() $\textbf{p}$
only;
$\textbf{p}$
only;
![]() $C_r$
denotes constants depending on
$C_r$
denotes constants depending on
![]() $\textbf{p}$
and the parameter r only. (As always, these may change from one occurrence to the next.)
$\textbf{p}$
and the parameter r only. (As always, these may change from one occurrence to the next.)
Theorem 14.1. Let
![]() $\Lambda_n$
be the distance profile of a conditioned Galton–Watson tree of order n, with an offspring distribution
$\Lambda_n$
be the distance profile of a conditioned Galton–Watson tree of order n, with an offspring distribution
![]() $\textbf{p}$
such that
$\textbf{p}$
such that
![]() $\mu(\textbf{p})=1$
and
$\mu(\textbf{p})=1$
and
![]() $\sigma^2(\textbf{p})<\infty$
.
$\sigma^2(\textbf{p})<\infty$
.
-
(i) Let
 $r\geqslant 1$
be a real number. Then, for all
$r\geqslant 1$
be a real number. Then, for all
 $i, n \geqslant 1$
, (119)
$i, n \geqslant 1$
, (119) \begin{align} {\mathbb E{}}[ \Lambda_n(i)^{r} ]\leqslant C_r n^{3r/2}e^{-ci^{2}/n}.\end{align}
\begin{align} {\mathbb E{}}[ \Lambda_n(i)^{r} ]\leqslant C_r n^{3r/2}e^{-ci^{2}/n}.\end{align}
-
(ii) Let
 $r\geqslant1$
be an integer, and suppose that
$r\geqslant1$
be an integer, and suppose that
 $\textbf{p}$
has a finite
$\textbf{p}$
has a finite
 $(r+1)th$
moment: (120)Then, for all
$(r+1)th$
moment: (120)Then, for all \begin{align} \sum_{k} k^{1+r}p_{k} < \infty.\end{align}
\begin{align} \sum_{k} k^{1+r}p_{k} < \infty.\end{align}
 $i, n \geqslant 1$
, (121)Furthermore, we may in this case combine (119) and (121) to
$i, n \geqslant 1$
, (121)Furthermore, we may in this case combine (119) and (121) to \begin{align} {\mathbb E{}}[ \Lambda_n(i)^{r} ]\leqslant C_r i^{r} n^{r}.\end{align}
(122)for all
\begin{align} {\mathbb E{}}[ \Lambda_n(i)^{r} ]\leqslant C_r i^{r} n^{r}.\end{align}
(122)for all \begin{align} {\mathbb E{}}[ \Lambda_n(i)^{r} ]\leqslant C_r i^r n^{r}e^{-ci^{2}/n},\end{align}
\begin{align} {\mathbb E{}}[ \Lambda_n(i)^{r} ]\leqslant C_r i^r n^{r}e^{-ci^{2}/n},\end{align}
 $i, n \geqslant 1$
.
$i, n \geqslant 1$
.
The proof is given later. Note that (122) trivially implies (121) and (changing
![]() $C_r$
and c) (119); conversely (119) and (121) imply (122) by considering
$C_r$
and c) (119); conversely (119) and (121) imply (122) by considering
![]() $i\leqslant n^{1/2}$
and
$i\leqslant n^{1/2}$
and
![]() $i>n^{1/2}$
separately.
$i>n^{1/2}$
separately.
The special case
![]() $r=1$
of (121), i.e.,
$r=1$
of (121), i.e.,
was proved in [16, Theorem 1.3]; note that when
![]() $r=1$
, (120) holds automatically by our assumption
$r=1$
, (120) holds automatically by our assumption
![]() $\sigma^2(\textbf{p})<\infty$
.
$\sigma^2(\textbf{p})<\infty$
.
Remark 14.2. The estimates above are natural analogues of estimates for the profile
![]() $L_n$
. First, as proved in [Reference Addario-Berry, Devroye and Janson1, Theorem 1.6], under the conditions in Theorem 14.1(i),
$L_n$
. First, as proved in [Reference Addario-Berry, Devroye and Janson1, Theorem 1.6], under the conditions in Theorem 14.1(i),
for all
![]() $i,n\geqslant1$
. Second, as proved in [Reference Janson29, Theorem 1.13], under the conditions in Theorem 14.1(ii),
$i,n\geqslant1$
. Second, as proved in [Reference Janson29, Theorem 1.13], under the conditions in Theorem 14.1(ii),
for all
![]() $i,n\geqslant1$
. The estimates (124)–(125) are used in our proof of Theorem 14.1.
$i,n\geqslant1$
. The estimates (124)–(125) are used in our proof of Theorem 14.1.
Remark 14.3. We do not know whether the moment assumption (120) really is necessary for the result. This assumption is necessary for the corresponding estimate (125) for the profile
![]() $L_n(i)$
, as noted in [Reference Addario-Berry, Devroye and Janson1], but the argument there does not apply to the distance profile. We state this as an open problem.
$L_n(i)$
, as noted in [Reference Addario-Berry, Devroye and Janson1], but the argument there does not apply to the distance profile. We state this as an open problem.
Remark 14.5. We also do not know whether the assumption that r is an integer is necessary in Theorem 14.1(i); we conjecture that it is not. (This assumption is used in the proof of (125) in [Reference Janson29].)
As an immediate consequence of Theorems 1.4 and 14.1, we obtain the corresponding results for the asymptotic profile
![]() $\Lambda_\textbf{e}$
.
$\Lambda_\textbf{e}$
.
Theorem 14.6. For any
![]() $r \geqslant 1$
and all
$r \geqslant 1$
and all
![]() $x\geqslant0$
,
$x\geqslant0$
,
Proof. Fix an offspring distribution
![]() $\textbf{p}$
with
$\textbf{p}$
with
![]() $\mu(\textbf{p})=1$
and all moments finite. (For example, we may choose a well-known example such as
$\mu(\textbf{p})=1$
and all moments finite. (For example, we may choose a well-known example such as
![]() ${Po}(1)$
or
${Po}(1)$
or
![]() ${Bi}(2,\frac12)$
.) Let
${Bi}(2,\frac12)$
.) Let
![]() $x\in(0,\infty)$
. Define
$x\in(0,\infty)$
. Define
![]() $i_n\,:\!=\,\lceil{2\sigma^{-1} xn^{1/2}}\rceil$
. Then
$i_n\,:\!=\,\lceil{2\sigma^{-1} xn^{1/2}}\rceil$
. Then
![]() $i_n/n^{1/2}\to 2x/\sigma$
as
$i_n/n^{1/2}\to 2x/\sigma$
as
![]() ${{n\to\infty}}$
, and (3) implies
${{n\to\infty}}$
, and (3) implies
Hence, Fatou’s lemma and (119) yield, for any
![]() $r\geqslant1$
,
$r\geqslant1$
,
Similarly, Fatou’s lemma and (121) yield
for integer
![]() $r\geqslant1$
; equivalently, the
$r\geqslant1$
; equivalently, the
![]() $L^r$
norm is estimated by
$L^r$
norm is estimated by
![]() $\lVert{\Lambda_\textbf{e}(x)}\rVert_r \leqslant C_r x$
. This estimate extends to all real
$\lVert{\Lambda_\textbf{e}(x)}\rVert_r \leqslant C_r x$
. This estimate extends to all real
![]() $r\geqslant1$
by Lyapounov’s inequality. Hence, (128) and (129) both hold for all
$r\geqslant1$
by Lyapounov’s inequality. Hence, (128) and (129) both hold for all
![]() $r\geqslant1$
, which yields (126) for
$r\geqslant1$
, which yields (126) for
![]() $x>0$
.
$x>0$
.
Finally, the result (126) is trivial for
![]() $x=0$
, since
$x=0$
, since
![]() $\Lambda_\textbf{e}(0)=0$
a.s.
$\Lambda_\textbf{e}(0)=0$
a.s.
Remark 14.7. The same argument shows that Theorem 1.2 and (124)–(125) imply
for any
![]() $r \geqslant 1$
and all
$r \geqslant 1$
and all
![]() $x\geqslant0$
.
$x\geqslant0$
.
The proof of Theorem 14.1 relies on an invariance property of the law of Galton–Watson trees under random re-rooting proved by Bertoin and Miermont [Reference Bertoin and Miermont9, Proposition 2]. A pointed tree is a pair (T, v), where T is an ordered rooted tree (also called planar rooted tree) and v is a vertex of T. We endow the space of pointed trees with the
![]() $\sigma$
-finite measure
$\sigma$
-finite measure
![]() ${\mathbb P{}}^{\bullet}$
defined by
${\mathbb P{}}^{\bullet}$
defined by
where
![]() ${\mathcal T}^{{\textbf{p}}}$
is a Galton–Watson tree with offspring distribution
${\mathcal T}^{{\textbf{p}}}$
is a Galton–Watson tree with offspring distribution
![]() $\textbf{p}$
such that
$\textbf{p}$
such that
![]() $\mu(\textbf{p})=1$
. We let
$\mu(\textbf{p})=1$
. We let
![]() ${\mathbb E{}}^{\bullet}$
denote the expectation under this ‘law’. In particular, the conditional law
${\mathbb E{}}^{\bullet}$
denote the expectation under this ‘law’. In particular, the conditional law
![]() ${\mathbb P{}}^{\bullet}(\, \cdot \, \mid |T|= n)$
on the space of pointed trees with n vertices is well defined and equals the distribution of
${\mathbb P{}}^{\bullet}(\, \cdot \, \mid |T|= n)$
on the space of pointed trees with n vertices is well defined and equals the distribution of
![]() $({\mathcal T}^{{\textbf{p}}}_{n}, v)$
where given the conditioned Galton–Watson tree
$({\mathcal T}^{{\textbf{p}}}_{n}, v)$
where given the conditioned Galton–Watson tree
![]() ${\mathcal T}^{{\textbf{p}}}_{n}$
of order n, v is a uniform random vertex of
${\mathcal T}^{{\textbf{p}}}_{n}$
of order n, v is a uniform random vertex of
![]() ${\mathcal T}^{{\textbf{p}}}_{n}$
.
${\mathcal T}^{{\textbf{p}}}_{n}$
.
Let us now describe the transformation of pointed trees of Bertoin and Miermont [Reference Bertoin and Miermont9, Section 4]. They work with planted planar trees; the base in the planted tree is useful since it implicitly specifies the ordering of the transformed tree. However, we ignore this detail and formulate their transformation for rooted trees; our formulation is easily seen to be equivalent to theirs. For any rooted planar tree T and vertex v of T, let
![]() $T_{v}$
be the fringe subtree of T rooted at v, and let
$T_{v}$
be the fringe subtree of T rooted at v, and let
![]() $T^{v}$
be the subtree of T obtained by deleting all the strict descendants of v in T. We define a new pointed tree
$T^{v}$
be the subtree of T obtained by deleting all the strict descendants of v in T. We define a new pointed tree
![]() $(\hat{T},{\hat{v}})$
in the following way. If v is the root, we do nothing, and let
$(\hat{T},{\hat{v}})$
in the following way. If v is the root, we do nothing, and let
![]() $\bigl({\hat{T},\hat{v}}\bigr)=(T,v)$
. Otherwise, first remove the edge e(v) between v and its parent pr(v) in T, and instead connect v to the root of T. We then re-root the resulting tree at pr(v) and obtain the new rooted tree
$\bigl({\hat{T},\hat{v}}\bigr)=(T,v)$
. Otherwise, first remove the edge e(v) between v and its parent pr(v) in T, and instead connect v to the root of T. We then re-root the resulting tree at pr(v) and obtain the new rooted tree
![]() $\hat{T}$
, which we point at
$\hat{T}$
, which we point at
![]() $\hat v = v$
. Note that
$\hat v = v$
. Note that
![]() $\hat T_{\hat v}=T_v$
, and that
$\hat T_{\hat v}=T_v$
, and that
![]() $\hat{T}^{\hat{v}}\setminus{\{{\hat v}\}}$
equals
$\hat{T}^{\hat{v}}\setminus{\{{\hat v}\}}$
equals
![]() $T^v\setminus{\{{v}\}}=T\setminus T_v$
rerooted at pr(v).
$T^v\setminus{\{{v}\}}=T\setminus T_v$
rerooted at pr(v).
Bertoin and Miermont [Reference Bertoin and Miermont9, Proposition 2 and its proof] and its proof establish that this transformation preserves the measure
![]() ${\mathbb P{}}^\bullet$
; this includes the following.
${\mathbb P{}}^\bullet$
; this includes the following.
Proposition 14.8. (Bertoin and Miermont [Reference Bertoin and Miermont9]). Under
![]() ${\mathbb P{}}^{\bullet}$
,
${\mathbb P{}}^{\bullet}$
,
![]() $(\hat{T}^{\hat{v}}, T_{v})$
and
$(\hat{T}^{\hat{v}}, T_{v})$
and
![]() $(T^{v}, T_{v})$
have the same ‘law’. Furthermore, the trees
$(T^{v}, T_{v})$
have the same ‘law’. Furthermore, the trees
![]() $T^{v}$
and
$T^{v}$
and
![]() $T_{v}$
are independent, with
$T_{v}$
are independent, with
![]() $T_{v}$
being a Galton–Watson tree with offspring distribution
$T_{v}$
being a Galton–Watson tree with offspring distribution
![]() $\textbf{p}$
.
$\textbf{p}$
.
Proof of Theorem 14.1. For a rooted plane tree T and
![]() $i \geqslant 0$
an integer, it will be convenient to write
$i \geqslant 0$
an integer, it will be convenient to write
![]() $Z_{i}(T)\,:\!=\,L_T(i)$
for the number of vertices at distance i from the root of T. For a vertex v in T, note that the number of vertices at distance
$Z_{i}(T)\,:\!=\,L_T(i)$
for the number of vertices at distance i from the root of T. For a vertex v in T, note that the number of vertices at distance
![]() $i \geqslant 1$
from v is less than or equal to
$i \geqslant 1$
from v is less than or equal to
![]() $Z_{i-1}(\hat{T}^{\hat{v}}) +Z_{i}(T_{v})$
. (Strict inequality may occur because of the extra vertex
$Z_{i-1}(\hat{T}^{\hat{v}}) +Z_{i}(T_{v})$
. (Strict inequality may occur because of the extra vertex
![]() $\hat v$
added in
$\hat v$
added in
![]() $\hat{T}^{\hat{v}}$
.) From (16), we thus obtain that if
$\hat{T}^{\hat{v}}$
.) From (16), we thus obtain that if
![]() $\Lambda_{T}$
is the distance profile of T defined in (14), then
$\Lambda_{T}$
is the distance profile of T defined in (14), then
If
![]() $r\geqslant1$
and
$r\geqslant1$
and
![]() $|T|=n$
, then (132) and Jensen’s inequality yield
$|T|=n$
, then (132) and Jensen’s inequality yield
Consequently, using (131),
 \begin{align} {\mathbb E{}}[ \Lambda_n(i)^{r} ] & \leqslant n^{r} {\mathbb E{}}^{\bullet} \bigl[{ \bigl({ Z_{i-1}(\hat{T}^{\hat{v}}) + Z_{i}(T_{v})}\bigr)^{r} \, \big | \, |T| = n }\bigr] \notag \\& \leqslant 2^{r} n^{r} {\mathbb E{}}^{\bullet} \bigl[{ Z_{i-1}(\hat{T}^{\hat{v}})^{r} + Z_{i}(T_{v})^{r} \, \big | \, |T| = n }\bigr].\end{align}
\begin{align} {\mathbb E{}}[ \Lambda_n(i)^{r} ] & \leqslant n^{r} {\mathbb E{}}^{\bullet} \bigl[{ \bigl({ Z_{i-1}(\hat{T}^{\hat{v}}) + Z_{i}(T_{v})}\bigr)^{r} \, \big | \, |T| = n }\bigr] \notag \\& \leqslant 2^{r} n^{r} {\mathbb E{}}^{\bullet} \bigl[{ Z_{i-1}(\hat{T}^{\hat{v}})^{r} + Z_{i}(T_{v})^{r} \, \big | \, |T| = n }\bigr].\end{align}
By Proposition 14.8, we have on the one hand that
 \begin{align} {\mathbb E{}}^{\bullet} \bigl[{ Z_{i-1}(\hat{T}^{\hat{v}})^{r} \, \big | \, |T| = n }\bigr] & = {\mathbb E{}}^{\bullet} \bigl[{ Z_{i-1}(T^{v})^{r} \, \big | \, |T| = n }\bigr] \notag \\& \leqslant {\mathbb E{}}^{\bullet} \bigl[{ Z_{i-1}(T)^{r} \, \big | \, |T| = n }\bigr] \notag \\& = {\mathbb E{}} [ Z_{i-1}( {\mathcal T}^{{\textbf{p}}}_{n})^{r} ].\end{align}
\begin{align} {\mathbb E{}}^{\bullet} \bigl[{ Z_{i-1}(\hat{T}^{\hat{v}})^{r} \, \big | \, |T| = n }\bigr] & = {\mathbb E{}}^{\bullet} \bigl[{ Z_{i-1}(T^{v})^{r} \, \big | \, |T| = n }\bigr] \notag \\& \leqslant {\mathbb E{}}^{\bullet} \bigl[{ Z_{i-1}(T)^{r} \, \big | \, |T| = n }\bigr] \notag \\& = {\mathbb E{}} [ Z_{i-1}( {\mathcal T}^{{\textbf{p}}}_{n})^{r} ].\end{align}
On the other hand, since
![]() $|T| = |T^{v}| + |T_{v}| -1$
, we see from Proposition 14.8 that
$|T| = |T^{v}| + |T_{v}| -1$
, we see from Proposition 14.8 that
 \begin{align}{\mathbb E{}}^{\bullet} \bigl[{ Z_{i}(T_{v})^{r} \, \big | \, |T| = n }\bigr] & = \sum_{m=1}^{n} {\mathbb E{}}^{\bullet} \bigl[{ Z_{i}(T_{v})^{r} \, \big | \, |T_{v}| = m, |T^{v}| = n-m+1 }\bigr] \notag \\& \times {\mathbb P{}}^{\bullet} \bigl[{ |T_{v}| = m \, \big | \, |T| = n }\bigr] \notag \\& = \sum_{m=1}^{n} {\mathbb E{}} \bigl[{ Z_{i}({\mathcal T}^{{\textbf{p}}}_{m})^{r} }\bigr] {\mathbb P{}}^{\bullet} \bigl[{ |T_{v}| = m \, \big | \, |T| = n }\bigr] \notag \\& \leqslant \sup_{1 \leqslant m \leqslant n} {\mathbb E{}} \bigl[{ Z_{i}({\mathcal T}^{{\textbf{p}}}_{m})^{r} }\bigr] .\end{align}
\begin{align}{\mathbb E{}}^{\bullet} \bigl[{ Z_{i}(T_{v})^{r} \, \big | \, |T| = n }\bigr] & = \sum_{m=1}^{n} {\mathbb E{}}^{\bullet} \bigl[{ Z_{i}(T_{v})^{r} \, \big | \, |T_{v}| = m, |T^{v}| = n-m+1 }\bigr] \notag \\& \times {\mathbb P{}}^{\bullet} \bigl[{ |T_{v}| = m \, \big | \, |T| = n }\bigr] \notag \\& = \sum_{m=1}^{n} {\mathbb E{}} \bigl[{ Z_{i}({\mathcal T}^{{\textbf{p}}}_{m})^{r} }\bigr] {\mathbb P{}}^{\bullet} \bigl[{ |T_{v}| = m \, \big | \, |T| = n }\bigr] \notag \\& \leqslant \sup_{1 \leqslant m \leqslant n} {\mathbb E{}} \bigl[{ Z_{i}({\mathcal T}^{{\textbf{p}}}_{m})^{r} }\bigr] .\end{align}
Combining (134), (135) and (136), we have that
 \begin{align} {\mathbb E{}}[ \Lambda_n(i)^{r} ]&\leqslant 2^{r} n^{r} \bigl({{\mathbb E{}} \bigl[{ Z_{i-1}( {\mathcal T}^{{\textbf{p}}}_{n})^{r} }\bigr]+ \sup_{1 \leqslant m \leqslant n} {\mathbb E{}} \bigl[{ Z_{i}({\mathcal T}^{{\textbf{p}}}_{m})^{r} }\bigr]}\bigr)\notag\\&= 2^{r} n^{r} \bigl({{\mathbb E{}} \bigl[{L_n(i-1)^{r} }\bigr]+ \sup_{1 \leqslant m \leqslant n} {\mathbb E{}} \bigl[{ L_m(i)^{r} }\bigr]}\bigr).\end{align}
\begin{align} {\mathbb E{}}[ \Lambda_n(i)^{r} ]&\leqslant 2^{r} n^{r} \bigl({{\mathbb E{}} \bigl[{ Z_{i-1}( {\mathcal T}^{{\textbf{p}}}_{n})^{r} }\bigr]+ \sup_{1 \leqslant m \leqslant n} {\mathbb E{}} \bigl[{ Z_{i}({\mathcal T}^{{\textbf{p}}}_{m})^{r} }\bigr]}\bigr)\notag\\&= 2^{r} n^{r} \bigl({{\mathbb E{}} \bigl[{L_n(i-1)^{r} }\bigr]+ \sup_{1 \leqslant m \leqslant n} {\mathbb E{}} \bigl[{ L_m(i)^{r} }\bigr]}\bigr).\end{align}
Therefore, (119) and (121) follow from (124) and (125), proved in [Reference Addario-Berry, Devroye and Janson1, Theorem 1.6] and [Reference Janson29, Theorem 1.13], respectively.
15. Hölder continuity
We now discuss Hölder continuity properties of the continuous random functions
![]() $L_\textbf{e}$
and
$L_\textbf{e}$
and
![]() $\Lambda_\textbf{e}$
. We begin with
$\Lambda_\textbf{e}$
. We begin with
![]() $L_\textbf{e}$
, the local time of
$L_\textbf{e}$
, the local time of
![]() $\textbf{e}$
. The results are to a large extent known, although we do not know any reference to the form of them stated here; nevertheless, we treat also
$\textbf{e}$
. The results are to a large extent known, although we do not know any reference to the form of them stated here; nevertheless, we treat also
![]() $L_\textbf{e}$
in detail, as a background to and preparation for the discussion of
$L_\textbf{e}$
in detail, as a background to and preparation for the discussion of
![]() $\Lambda_\textbf{e}$
below.
$\Lambda_\textbf{e}$
below.
It is well known that the local time of Brownian motion at some fixed time a.s. is Hölder continuous of order
![]() $\alpha$
for any
$\alpha$
for any
![]() $\alpha <1/2$
, see [Reference Revuz and Yor49, VI.(1.8)]. It is also known that this Hölder continuity extends by standard arguments to the local times of Brownian bridge and Brownian excursion, and thus (see Theorem 1.2) to
$\alpha <1/2$
, see [Reference Revuz and Yor49, VI.(1.8)]. It is also known that this Hölder continuity extends by standard arguments to the local times of Brownian bridge and Brownian excursion, and thus (see Theorem 1.2) to
![]() $L_\textbf{e}$
. We need a quantitative version of this.
$L_\textbf{e}$
. We need a quantitative version of this.
For
![]() $\alpha>0$
and an interval
$\alpha>0$
and an interval
![]() $I\subseteq\mathbb R$
, let the Hölder space
$I\subseteq\mathbb R$
, let the Hölder space
![]() $\mathcal H_\alpha=\mathcal H_\alpha(I)$
be the space of functions
$\mathcal H_\alpha=\mathcal H_\alpha(I)$
be the space of functions
![]() $f\,:\,I\to\mathbb R$
such that
$f\,:\,I\to\mathbb R$
such that
This is a semi-norm. We may regard
![]() $\mathcal H_\alpha$
as a space of functions modulo constants, and then
$\mathcal H_\alpha$
as a space of functions modulo constants, and then
![]() $\lVert{\cdot}\rVert_{\mathcal H_\alpha}$
is a norm and
$\lVert{\cdot}\rVert_{\mathcal H_\alpha}$
is a norm and
![]() $\mathcal H_\alpha$
a Banach space.
$\mathcal H_\alpha$
a Banach space.
Theorem 15.1. Let
![]() $0<\alpha<\frac12$
and let
$0<\alpha<\frac12$
and let
![]() $A<\infty$
. Then
$A<\infty$
. Then
In particular,
![]() $L_\textbf{e}\in\mathcal H_\alpha[0,\infty)$
a.s.
$L_\textbf{e}\in\mathcal H_\alpha[0,\infty)$
a.s.
Proof. We let
![]() $\alpha$
and A be fixed. Constants C below may depend on
$\alpha$
and A be fixed. Constants C below may depend on
![]() $\alpha$
and A.
$\alpha$
and A.
Recall that
![]() $L_\textbf{e}(x)=L^x_1$
, where
$L_\textbf{e}(x)=L^x_1$
, where
![]() $L^x_t$
is the local time of a (standard) Brownian excursion
$L^x_t$
is the local time of a (standard) Brownian excursion
![]() $\textbf{e}$
. The proof will actually show the result for
$\textbf{e}$
. The proof will actually show the result for
![]() $L^x_t$
for any fixed
$L^x_t$
for any fixed
![]() $t\in{[0,1]}$
.
$t\in{[0,1]}$
.
We first note that if
![]() $\beta$
is a 3-dimensional Bessel process started from 0 (see e.g. [Reference Revuz and Yor49, Section VI.3]), then a standard Brownian excursion
$\beta$
is a 3-dimensional Bessel process started from 0 (see e.g. [Reference Revuz and Yor49, Section VI.3]), then a standard Brownian excursion
![]() $\textbf{e}$
is given by
$\textbf{e}$
is given by
![]() $\textbf{e}(1)=0$
and
$\textbf{e}(1)=0$
and
see [Reference Blumenthal13, II.(1.5)]. One then can deduce from [Reference Revuz and Yor49, VI.(3.3)] and an application of the Itô integration by parts formula that
![]() $\textbf{e}$
satisfies
$\textbf{e}$
satisfies
where B is a standard Brownian motion. In particular,
![]() $\textbf{e}$
is a continuous semi-martingale.
$\textbf{e}$
is a continuous semi-martingale.
We now follow the proof of [Reference Revuz and Yor49, VI.(1.7), see also VI.(1.32)], but avoid localising at the cost of further calculations. Let
so (141) can be written
Then, by Tanaka’s formula [Reference Revuz and Yor49, VI.(1.2)], writing
![]() $x^+\,:\!=\,x\lor 0$
,
$x^+\,:\!=\,x\lor 0$
,
 \begin{align} L^x_t = 2 \bigl({\textbf{e}(t)-x}\bigr)^+- 2 \bigl({-x}\bigr)^+&-2\int_0^t \boldsymbol1\{{{\textbf{e}(s)>x}}\}\,\textrm{d} B(s)\notag\\&\qquad-2\int_0^t \boldsymbol1\{{{\textbf{e}(t)>x}}\} \textbf{v}(s)\,\textrm{d} s.\end{align}
\begin{align} L^x_t = 2 \bigl({\textbf{e}(t)-x}\bigr)^+- 2 \bigl({-x}\bigr)^+&-2\int_0^t \boldsymbol1\{{{\textbf{e}(s)>x}}\}\,\textrm{d} B(s)\notag\\&\qquad-2\int_0^t \boldsymbol1\{{{\textbf{e}(t)>x}}\} \textbf{v}(s)\,\textrm{d} s.\end{align}
Fix
![]() $t\in{[0,1]}$
and denote the four random functions of x on the right-hand side of (144) by
$t\in{[0,1]}$
and denote the four random functions of x on the right-hand side of (144) by
![]() $F_1(x),\dots,F_4(x)$
. Trivially, the first two are in
$F_1(x),\dots,F_4(x)$
. Trivially, the first two are in
![]() $\mathcal H_1$
(= Lipschitz), with norm at most 2. Hence,
$\mathcal H_1$
(= Lipschitz), with norm at most 2. Hence,
For each x,
![]() $F_3(x)$
is a continuous martingale in t. Thus, if
$F_3(x)$
is a continuous martingale in t. Thus, if
![]() $0\leqslant x<y\leqslant A$
, the Burkholder–Davis–Gundy inequality [Reference Revuz and Yor49, IV.(4.1)] and the occupation times formula [Reference Revuz and Yor49, VI.(1.9)] yield, for any
$0\leqslant x<y\leqslant A$
, the Burkholder–Davis–Gundy inequality [Reference Revuz and Yor49, IV.(4.1)] and the occupation times formula [Reference Revuz and Yor49, VI.(1.9)] yield, for any
![]() $p\geqslant2$
,
$p\geqslant2$
,
 \begin{align} {\mathbb E{}} |F_3(x)-F_3(y)|^p&\leqslant C_p {\mathbb E{}} \Bigl[{\Bigl({\int_0^t \boldsymbol1\{{{x<\textbf{e}(s)\leqslant y}}\}\,\textrm{d} s}\Bigr)^{p/2}}\Bigr]\notag\\&= C_p {\mathbb E{}} \Bigl[{\Bigl({\int_x^y L^z_t\,\textrm{d} z}\Bigr)^{p/2}}\Bigr]\notag\\&= C_p (y-x)^{p/2}{\mathbb E{}} \Bigl[{\Bigl({\frac{1}{y-x}\int_x^y L^z_t\,\textrm{d} z}\Bigr)^{p/2}}\Bigr]\notag\\&\leqslant C_p (y-x)^{p/2}{\mathbb E{}} \Bigl[{{\frac{1}{y-x}\int_x^y \bigl({L^z_t}\bigr)^{p/2}\,\textrm{d} z}}\Bigr].\notag\\&= C_p (y-x)^{p/2}{\frac{1}{y-x}\int_x^y {\mathbb E{}}\bigl({L^z_t}\bigr)^{p/2}\,\textrm{d} z}.\end{align}
\begin{align} {\mathbb E{}} |F_3(x)-F_3(y)|^p&\leqslant C_p {\mathbb E{}} \Bigl[{\Bigl({\int_0^t \boldsymbol1\{{{x<\textbf{e}(s)\leqslant y}}\}\,\textrm{d} s}\Bigr)^{p/2}}\Bigr]\notag\\&= C_p {\mathbb E{}} \Bigl[{\Bigl({\int_x^y L^z_t\,\textrm{d} z}\Bigr)^{p/2}}\Bigr]\notag\\&= C_p (y-x)^{p/2}{\mathbb E{}} \Bigl[{\Bigl({\frac{1}{y-x}\int_x^y L^z_t\,\textrm{d} z}\Bigr)^{p/2}}\Bigr]\notag\\&\leqslant C_p (y-x)^{p/2}{\mathbb E{}} \Bigl[{{\frac{1}{y-x}\int_x^y \bigl({L^z_t}\bigr)^{p/2}\,\textrm{d} z}}\Bigr].\notag\\&= C_p (y-x)^{p/2}{\frac{1}{y-x}\int_x^y {\mathbb E{}}\bigl({L^z_t}\bigr)^{p/2}\,\textrm{d} z}.\end{align}
We have
![]() $L^z_t \leqslant L^z_1=L_\textbf{e}(z)$
, and thus (130) implies
$L^z_t \leqslant L^z_1=L_\textbf{e}(z)$
, and thus (130) implies
![]() ${\mathbb E{}}(L^z_t)^{p/2}\leqslant C_p$
for all z; hence (146) yields
${\mathbb E{}}(L^z_t)^{p/2}\leqslant C_p$
for all z; hence (146) yields
Consequently,
![]() $F_3$
satisfies the Kolmogorov continuity criterion, and the version of it stated in [Reference Revuz and Yor49, I.(2.1)] shows that if p is chosen so large that
$F_3$
satisfies the Kolmogorov continuity criterion, and the version of it stated in [Reference Revuz and Yor49, I.(2.1)] shows that if p is chosen so large that
![]() $(p/2-1)/p > \alpha$
, then (147) implies
$(p/2-1)/p > \alpha$
, then (147) implies
Similarly, using the extension of the occupation times formula in [Reference Revuz and Yor49, VI.(1.15)], if again
![]() $0\leqslant x<y\leqslant A$
,
$0\leqslant x<y\leqslant A$
,
 \begin{align} F_4(y)-F_4(x)&=2\int_0^t\boldsymbol1\{{{x<\textbf{e}(s)\leqslant y}}\}\textbf{v}(s)\,\textrm{d} s\notag\\&=2\int_0^t\boldsymbol1\{{{x<\textbf{e}(s)\leqslant y}}\}\Bigl({\frac{1}{\textbf{e}(s)} - \frac{\textbf{e}(s)}{1-s}}\Bigr)\,\textrm{d} s\notag\\&=2\int_x^y\,\textrm{d} z\int_0^t \Bigl({\frac{1}{z} - \frac{z}{1-s}}\Bigr)\,\textrm{d} L^z_s.\end{align}
\begin{align} F_4(y)-F_4(x)&=2\int_0^t\boldsymbol1\{{{x<\textbf{e}(s)\leqslant y}}\}\textbf{v}(s)\,\textrm{d} s\notag\\&=2\int_0^t\boldsymbol1\{{{x<\textbf{e}(s)\leqslant y}}\}\Bigl({\frac{1}{\textbf{e}(s)} - \frac{\textbf{e}(s)}{1-s}}\Bigr)\,\textrm{d} s\notag\\&=2\int_x^y\,\textrm{d} z\int_0^t \Bigl({\frac{1}{z} - \frac{z}{1-s}}\Bigr)\,\textrm{d} L^z_s.\end{align}
We now simplify and assume
![]() $0\leqslant t\leqslant \frac12$
. Then (149) implies
$0\leqslant t\leqslant \frac12$
. Then (149) implies
Let
![]() $p'\,:\!=\,1/\alpha$
and let
$p'\,:\!=\,1/\alpha$
and let
![]() $p\,:\!=\,(1-\alpha)^{-1}>1$
be the conjugate exponent. Then, by (150) and Hölder’s inequality,
$p\,:\!=\,(1-\alpha)^{-1}>1$
be the conjugate exponent. Then, by (150) and Hölder’s inequality,
Consequently,
Thus, using again (130),
and thus
Consequently, (144), (145), (148) and (154) yield
for
![]() $0\leqslant t\leqslant\frac12$
.
$0\leqslant t\leqslant\frac12$
.
We have for simplicity assumed
![]() $t\leqslant\frac12$
. To complete the proof, we note that
$t\leqslant\frac12$
. To complete the proof, we note that
![]() $\textbf{e}$
is invariant under reflection:
$\textbf{e}$
is invariant under reflection:
![]() $\textbf{e}(1-t)\overset{\textrm{d}}{=}\textbf{e}(t)$
(as processes), and thus
$\textbf{e}(1-t)\overset{\textrm{d}}{=}\textbf{e}(t)$
(as processes), and thus
![]() $L^x_1-L^x_{1/2}\overset{\textrm{d}}{=} L^x_{1/2}$
(as processes in x). Consequently,
$L^x_1-L^x_{1/2}\overset{\textrm{d}}{=} L^x_{1/2}$
(as processes in x). Consequently,
showing (139). (The case
![]() $\frac12<t<1$
follows similarly.)
$\frac12<t<1$
follows similarly.)
Finally, (139) shows that a.s.,
![]() $L_\textbf{e}\in\mathcal H_\alpha[0,A]$
for every
$L_\textbf{e}\in\mathcal H_\alpha[0,A]$
for every
![]() $A>0$
. Moreover,
$A>0$
. Moreover,
![]() $L_\textbf{e}$
has finite support
$L_\textbf{e}$
has finite support
![]() $[0, \sup\textbf{e}]$
, and thus
$[0, \sup\textbf{e}]$
, and thus
![]() $L_\textbf{e}\in\mathcal H_\alpha[0,\infty)$
.
$L_\textbf{e}\in\mathcal H_\alpha[0,\infty)$
.
We have for simplicity considered a finite interval [0, A] in Theorem 15.1, but the result can easily be extended to
![]() $\mathcal H_\alpha[0,\infty)$
.
$\mathcal H_\alpha[0,\infty)$
.
Theorem 15.2. Let
![]() $0<\alpha<\frac12$
. Then
$0<\alpha<\frac12$
. Then
Proof. Note that the proof of Theorem 15.1 actually shows
![]() ${\mathbb E{}}\,\lVert{{L_\textbf{e}}}\rVert_{\mathcal H_\alpha[0,A]}^p<\infty$
for some
${\mathbb E{}}\,\lVert{{L_\textbf{e}}}\rVert_{\mathcal H_\alpha[0,A]}^p<\infty$
for some
![]() $p>1$
, see (148) and (153). Moreover, the same proof applied to the interval
$p>1$
, see (148) and (153). Moreover, the same proof applied to the interval
![]() $[m,m+1]$
shows that for any
$[m,m+1]$
shows that for any
![]() $m\geqslant1$
,
$m\geqslant1$
,
with C independent of m, where the factor
![]() $m^p$
comes from (150). Furthermore,
$m^p$
comes from (150). Furthermore,
![]() $L_\textbf{e}=0$
on
$L_\textbf{e}=0$
on
![]() $[m,m+1]$
unless
$[m,m+1]$
unless
![]() $\sup\textbf{e}>m$
. The explicit formula for the distribution function of
$\sup\textbf{e}>m$
. The explicit formula for the distribution function of
![]() $\sup\textbf{e}$
, see e.g. [Reference Chung15, Reference Kennedy33] or [Reference Drmota17, p. 114], yields the well-known subgaussian decay
$\sup\textbf{e}$
, see e.g. [Reference Chung15, Reference Kennedy33] or [Reference Drmota17, p. 114], yields the well-known subgaussian decay
(See also [Reference Addario-Berry, Devroye and Janson1] for the corresponding result for heights of conditioned Galton–Watson trees.) Combining (158) and (159) with Hölder’s inequality, we obtain, with
![]() $1/q=1-1/p$
,
$1/q=1-1/p$
,
 \begin{align} {\mathbb E{}}\,\lVert{{L_\textbf{e}}}\rVert_{\mathcal H_\alpha{[m,m+1]}}&\leqslant \Bigl({{\mathbb E{}}\,\lVert{{L_\textbf{e}}}\rVert_{\mathcal H_\alpha{[m,m+1]}}^p}\Bigr)^{1/p}{\mathbb P{}}\bigl({\lVert{{L_\textbf{e}}}\rVert_{\mathcal H_\alpha{[m,m+1]}}\neq0}\bigr)^{1/q}\notag\\&\leqslant Cm {\mathbb P{}}\bigl({\sup\textbf{e}>m}\bigr)^{1/q}\leqslant Cm e^{-cm^2},\end{align}
\begin{align} {\mathbb E{}}\,\lVert{{L_\textbf{e}}}\rVert_{\mathcal H_\alpha{[m,m+1]}}&\leqslant \Bigl({{\mathbb E{}}\,\lVert{{L_\textbf{e}}}\rVert_{\mathcal H_\alpha{[m,m+1]}}^p}\Bigr)^{1/p}{\mathbb P{}}\bigl({\lVert{{L_\textbf{e}}}\rVert_{\mathcal H_\alpha{[m,m+1]}}\neq0}\bigr)^{1/q}\notag\\&\leqslant Cm {\mathbb P{}}\bigl({\sup\textbf{e}>m}\bigr)^{1/q}\leqslant Cm e^{-cm^2},\end{align}
Finally, it is easy to see that
Remark 15.3. The proofs above apply also to the local time of the Brownian bridge. The main differences are that we consider functions on
![]() $(-\infty,\infty)$
and that the term
$(-\infty,\infty)$
and that the term
![]() $1/\textbf{e}(t)$
in (142) disappears. This shows that, writing
$1/\textbf{e}(t)$
in (142) disappears. This shows that, writing
![]() ${L}_{\textbf{b}}(x)$
for the local time of the Brownian bridge at time
${L}_{\textbf{b}}(x)$
for the local time of the Brownian bridge at time
![]() $t=1$
,
$t=1$
,
By Vervaat [Reference Vervaat51], the Brownian excursion can be constructed from a Brownian bridge by shifts in both time and space, and thus
![]() $L_\textbf{e}$
is a (random) shift of
$L_\textbf{e}$
is a (random) shift of
![]() ${L}_{\textbf{b}}$
. Consequently, with this coupling,
${L}_{\textbf{b}}$
. Consequently, with this coupling,
and thus (157) and (163) are equivalent. This yields an alternative proof of Theorem 15.2.
We have so far considered
![]() $\alpha<1/2$
. For
$\alpha<1/2$
. For
![]() $\alpha\geqslant1/2$
, it is well known that Brownian motion is a.s. not locally Hölder(
$\alpha\geqslant1/2$
, it is well known that Brownian motion is a.s. not locally Hölder(
![]() $\alpha$
); see e.g. [Reference Revuz and Yor49, I.(2.7)] or [Reference Mörters and Peres43, Section 1.2] for even more precise results. Moreover, the same holds for the local time
$\alpha$
); see e.g. [Reference Revuz and Yor49, I.(2.7)] or [Reference Mörters and Peres43, Section 1.2] for even more precise results. Moreover, the same holds for the local time
![]() $\bar{L}^x_t$
of Brownian motion, regarded as a function of the space variable x (for any fixed
$\bar{L}^x_t$
of Brownian motion, regarded as a function of the space variable x (for any fixed
![]() $t>0$
); we do not know an explicit reference but this follows easily, for example, from the first Ray–Knight theorem [Reference Revuz and Yor49, XI.(2.2)], which says that if we stop at
$t>0$
); we do not know an explicit reference but this follows easily, for example, from the first Ray–Knight theorem [Reference Revuz and Yor49, XI.(2.2)], which says that if we stop at
![]() $\tau_1$
, the hitting time of 1, then the process
$\tau_1$
, the hitting time of 1, then the process
![]() $(\bar{L}^{1-x}_{\tau_1})$
,
$(\bar{L}^{1-x}_{\tau_1})$
,
![]() $0\leqslant x\leqslant 1$
, is a 2-dimensional squared Bessel process, which (at least away from 0) has the same smoothness as a Brownian motion (since it can be written as the sum of squares of two independent Brownian motions); we omit the details.
$0\leqslant x\leqslant 1$
, is a 2-dimensional squared Bessel process, which (at least away from 0) has the same smoothness as a Brownian motion (since it can be written as the sum of squares of two independent Brownian motions); we omit the details.
Similarly,
![]() $L_\textbf{e}=L^x_1$
, which is the local time of a standard Brownian excursion is a.s. not Hölder(
$L_\textbf{e}=L^x_1$
, which is the local time of a standard Brownian excursion is a.s. not Hölder(
![]() $\frac12$
). One way to see this is that if we stop a Brownian motion when its local time at 0 reaches 1, i.e., at
$\frac12$
). One way to see this is that if we stop a Brownian motion when its local time at 0 reaches 1, i.e., at
![]() $\tau\,:\!=\,\inf{\{{t\,:\,\bar{L}^0_t=1}\}}$
, then the part of the Brownian motion before time
$\tau\,:\!=\,\inf{\{{t\,:\,\bar{L}^0_t=1}\}}$
, then the part of the Brownian motion before time
![]() $\tau$
and above any fixed
$\tau$
and above any fixed
![]() $\delta>0$
is a.s. included in a finite number of excursions, and these are independent, conditioned on the number of them and their lengths. Hence, if the local time of a Brownian excursion were Hölder(
$\delta>0$
is a.s. included in a finite number of excursions, and these are independent, conditioned on the number of them and their lengths. Hence, if the local time of a Brownian excursion were Hölder(
![]() $\frac12$
) with positive probability, then so would
$\frac12$
) with positive probability, then so would
![]() $\bar{L}_\tau^x$
, restricted to
$\bar{L}_\tau^x$
, restricted to
![]() $x\geqslant\delta$
, be, and then
$x\geqslant\delta$
, be, and then
![]() $\bar{L}_t^x$
,
$\bar{L}_t^x$
,
![]() $x\geqslant\delta$
, would be Hölder(
$x\geqslant\delta$
, would be Hölder(
![]() $\frac12$
) with positive probability for some rational t, and thus for all
$\frac12$
) with positive probability for some rational t, and thus for all
![]() $t>0$
by scaling, which contradicts the argument above.
$t>0$
by scaling, which contradicts the argument above.
15.1. Distance profile
We next consider the asymptotic distance profile
![]() $\Lambda_\textbf{e}$
. We first note that the nice re-rooting invariance property of the standard Brownian excursion
$\Lambda_\textbf{e}$
. We first note that the nice re-rooting invariance property of the standard Brownian excursion
![]() $\textbf{e}$
presented in Section 2.3 yields the following corollary of Theorem 15.2.
$\textbf{e}$
presented in Section 2.3 yields the following corollary of Theorem 15.2.
Corollary 15.4. Let
![]() $0<\alpha<\frac12$
. Then
$0<\alpha<\frac12$
. Then
In particular, the random function
![]() $\Lambda_\textbf{e}\in\mathcal H_\alpha[0,\infty)$
a.s.
$\Lambda_\textbf{e}\in\mathcal H_\alpha[0,\infty)$
a.s.
Proof. It follows from the identity (24) that
where for every
![]() $s \in{[0,1]}$
,
$s \in{[0,1]}$
,
![]() $L_{\textbf{e}^{[s]}}$
denotes the local time of the process
$L_{\textbf{e}^{[s]}}$
denotes the local time of the process
![]() $\textbf{e}^{[s]}$
defined in (22), which is distributed as a standard Brownian excursion (23). Hence, Theorem 15.2 yields
$\textbf{e}^{[s]}$
defined in (22), which is distributed as a standard Brownian excursion (23). Hence, Theorem 15.2 yields
However, it turns out that the averaging in (24) actually makes
![]() $\Lambda_\textbf{e}$
smoother than
$\Lambda_\textbf{e}$
smoother than
![]() $L_\textbf{e}$
; we have the following stronger result, which improves Corollary 15.4.
$L_\textbf{e}$
; we have the following stronger result, which improves Corollary 15.4.
Theorem 15.5. The asymptotic distance profile
![]() $\Lambda_{{\textbf{e}}}\in \mathcal H_\alpha$
for every
$\Lambda_{{\textbf{e}}}\in \mathcal H_\alpha$
for every
![]() $\alpha<1$
, a.s. Furthermore,
$\alpha<1$
, a.s. Furthermore,
![]() $\Lambda_\textbf{e}$
is a.s. absolutely continuous and with a derivative
$\Lambda_\textbf{e}$
is a.s. absolutely continuous and with a derivative
![]() $\Lambda_{{\textbf{e}}}'$
(defined a.e.) that belongs to
$\Lambda_{{\textbf{e}}}'$
(defined a.e.) that belongs to
![]() $L^p(\mathbb R)$
for every
$L^p(\mathbb R)$
for every
![]() $p<\infty$
.
$p<\infty$
.
In order to prove Theorem 15.5, we first prove an estimate of the Fourier transform of
![]() $\Lambda_\textbf{e}$
. We choose to define Fourier transforms as, for
$\Lambda_\textbf{e}$
. We choose to define Fourier transforms as, for
![]() $f\in L^1(\mathbb R)$
,
$f\in L^1(\mathbb R)$
,
Note that by (21), the Fourier transform
![]() $\widehat{\Lambda_\textbf{e}}$
can be written as
$\widehat{\Lambda_\textbf{e}}$
can be written as
Lemma 15.6. There exists a constant C such that
Proof. Note first that the profile
![]() $\Lambda_\textbf{e}$
is a (random) non-negative function with integral 1, e.g., by (4). Hence, for every
$\Lambda_\textbf{e}$
is a (random) non-negative function with integral 1, e.g., by (4). Hence, for every
![]() $\xi$
,
$\xi$
,
Thus, (170) is trivial for
![]() $|\xi|\leqslant1$
. Assume in the remainder of the proof
$|\xi|\leqslant1$
. Assume in the remainder of the proof
![]() $|\xi|\geqslant1$
.
$|\xi|\geqslant1$
.
By (169),
 \begin{align} {\mathbb E{}}\,\bigl\lvert{\widehat{\Lambda_\textbf{e}}(\xi)}\bigr\rvert^2&={\mathbb E{}} \idotsint_{t_1,\dots t_4\in{[0,1]}} e^{\textrm{i} \xi (\textsf{d}(t_1,t_2;\,\textbf{e})-\textsf{d}(t_3,t_4;\,\textbf{e}))}\,\textrm{d} t_1\dotsm\,\textrm{d} t_4\notag\\&={\mathbb E{}} e^{\textrm{i} \xi (\textsf{d}(U_1,U_2;\,\textbf{e})-\textsf{d}(U_3,U_4;\,\textbf{e}))},\end{align}
\begin{align} {\mathbb E{}}\,\bigl\lvert{\widehat{\Lambda_\textbf{e}}(\xi)}\bigr\rvert^2&={\mathbb E{}} \idotsint_{t_1,\dots t_4\in{[0,1]}} e^{\textrm{i} \xi (\textsf{d}(t_1,t_2;\,\textbf{e})-\textsf{d}(t_3,t_4;\,\textbf{e}))}\,\textrm{d} t_1\dotsm\,\textrm{d} t_4\notag\\&={\mathbb E{}} e^{\textrm{i} \xi (\textsf{d}(U_1,U_2;\,\textbf{e})-\textsf{d}(U_3,U_4;\,\textbf{e}))},\end{align}
where
![]() $U_1,\dots,U_4$
are i.i.d. uniform U(0,1) random variables, independent of
$U_1,\dots,U_4$
are i.i.d. uniform U(0,1) random variables, independent of
![]() $\textbf{e}$
.
$\textbf{e}$
.
Recall from Section 2.3 that the Brownian excursion
![]() $\textbf{e}$
defines the continuum random tree
$\textbf{e}$
defines the continuum random tree
![]() $T_{\textbf{e}}$
, with a quotient map
$T_{\textbf{e}}$
, with a quotient map
![]() $\rho_{\textbf{e}}\,:\,{[0,1]}\to T_{\textbf{e}}$
. Let
$\rho_{\textbf{e}}\,:\,{[0,1]}\to T_{\textbf{e}}$
. Let
![]() $\overline{U}_i\,:\!=\,\rho_\textbf{e}(U_i)$
,
$\overline{U}_i\,:\!=\,\rho_\textbf{e}(U_i)$
,
![]() $i=1,\dots,4$
, be the points in
$i=1,\dots,4$
, be the points in
![]() $T_{\textbf{e}}$
corresponding to
$T_{\textbf{e}}$
corresponding to
![]() $U_i$
; these are i.i.d. uniformly random points in
$U_i$
; these are i.i.d. uniformly random points in
![]() $T_{\textbf{e}}$
, and
$T_{\textbf{e}}$
, and
![]() $\textsf{d}(U_i,U_j;\,\textbf{e})$
equals the distance
$\textsf{d}(U_i,U_j;\,\textbf{e})$
equals the distance
![]() $\textsf{d}(\overline{U}_i,\overline{U}_j)$
between
$\textsf{d}(\overline{U}_i,\overline{U}_j)$
between
![]() $\overline{U}_i$
and
$\overline{U}_i$
and
![]() $\overline{U}_j$
in the real tree
$\overline{U}_j$
in the real tree
![]() $T_{\textbf{e}}$
. Then (172) becomes
$T_{\textbf{e}}$
. Then (172) becomes
Furthermore, we can simplify the calculations by rerooting
![]() $T_{\textbf{e}}$
at
$T_{\textbf{e}}$
at
![]() $\overline{U}_4$
; this preserves the distribution, see (23), and
$\overline{U}_4$
; this preserves the distribution, see (23), and
![]() $\overline{U}_1,\dots,\overline{U}_3$
are still independent uniformly random points in the tree; hence, we also have, with
$\overline{U}_1,\dots,\overline{U}_3$
are still independent uniformly random points in the tree; hence, we also have, with
![]() $o=\rho_\textbf{e}(0)$
the root of
$o=\rho_\textbf{e}(0)$
the root of
![]() $T_{\textbf{e}}$
.
$T_{\textbf{e}}$
.
To calculate (174), it suffices to consider the (real) subtree of
![]() $T_{\textbf{e}}$
spanned by the root o and
$T_{\textbf{e}}$
spanned by the root o and
![]() $\overline{U}_{1},\dots,\overline{U}_3$
. [Reference Aldous4, Corollary 22] showed that the distribution of the random real tree
$\overline{U}_{1},\dots,\overline{U}_3$
. [Reference Aldous4, Corollary 22] showed that the distribution of the random real tree
![]() $\widetilde{{\mathcal T}}_k$
spanned in this way by
$\widetilde{{\mathcal T}}_k$
spanned in this way by
![]() $k\geqslant1$
i.i.d. uniform random points
$k\geqslant1$
i.i.d. uniform random points
![]() $\overline{U}_1,\dots,\overline{U}_k\in T_{\textbf{e}}$
can be described as follows. Let the shape
$\overline{U}_1,\dots,\overline{U}_k\in T_{\textbf{e}}$
can be described as follows. Let the shape
![]() $\tau$
of
$\tau$
of
![]() $\widetilde{{\mathcal T}}_k$
be the tree regarded as a combinatorial tree, i.e., ignoring the edge lengths. Then
$\widetilde{{\mathcal T}}_k$
be the tree regarded as a combinatorial tree, i.e., ignoring the edge lengths. Then
![]() $\tau$
is a.s. a rooted binary tree with k leaves, labelled by
$\tau$
is a.s. a rooted binary tree with k leaves, labelled by
![]() $1,\dots,k$
(corresponding to
$1,\dots,k$
(corresponding to
![]() $\overline{U}_1,\dots,\overline{U}_k$
). Let
$\overline{U}_1,\dots,\overline{U}_k$
). Let
![]() $\bar{\mathfrak{T}}^{k}$
be the set of possible shapes, i.e., the set of binary trees with k labelled leaves. Then
$\bar{\mathfrak{T}}^{k}$
be the set of possible shapes, i.e., the set of binary trees with k labelled leaves. Then
![]() $|\bar{\mathfrak{T}}^{k}|=(2k-3)!!$
. Each shape
$|\bar{\mathfrak{T}}^{k}|=(2k-3)!!$
. Each shape
![]() $\tau$
has
$\tau$
has
![]() $k-1$
internal vertices, and thus 2k vertices and
$k-1$
internal vertices, and thus 2k vertices and
![]() $2k-1$
edges. For each shape
$2k-1$
edges. For each shape
![]() $\tau$
, label the edges
$\tau$
, label the edges
![]() $1,\dots,2k-1$
in some order, and for each tree
$1,\dots,2k-1$
in some order, and for each tree
![]() $\widetilde{{\mathcal T}}_k$
with shape
$\widetilde{{\mathcal T}}_k$
with shape
![]() $\tau$
, let
$\tau$
, let
![]() $\ell_1,\dots,\ell_{2k-1}$
be the corresponding edge lengths. Then
$\ell_1,\dots,\ell_{2k-1}$
be the corresponding edge lengths. Then
![]() $\widetilde{{\mathcal T}}_k$
is described by
$\widetilde{{\mathcal T}}_k$
is described by
![]() $(\tau,\ell_1,\dots,\ell_k)$
, and the distribution of
$(\tau,\ell_1,\dots,\ell_k)$
, and the distribution of
![]() $(\tau,\ell_1,\dots,\ell_k)$
is given by the density, for
$(\tau,\ell_1,\dots,\ell_k)$
is given by the density, for
![]() $\tau\in\bar{\mathfrak{T}}^{k}$
and
$\tau\in\bar{\mathfrak{T}}^{k}$
and
![]() $\ell_i>0$
,
$\ell_i>0$
,
Recall that our normalisation differs from [Reference Aldous4], where
![]() $T_{2\textbf{e}}$
is used instead of
$T_{2\textbf{e}}$
is used instead of
![]() $T_{\textbf{e}}$
, and thus all edges are twice as long; hence (175) is obtained from [4, (33)] by a trivial change of variables.
$T_{\textbf{e}}$
, and thus all edges are twice as long; hence (175) is obtained from [4, (33)] by a trivial change of variables.
For
![]() $k=3$
we have
$k=3$
we have
![]() $|\bar{\mathfrak{T}}^{3}|=3!!=3$
different shapes. It is easy to verify that in each of them, we may label the five edges such that
$|\bar{\mathfrak{T}}^{3}|=3!!=3$
different shapes. It is easy to verify that in each of them, we may label the five edges such that
![]() $\textsf{d}(\overline{U}_1,\overline{U}_2)-\textsf{d}(\overline{U}_3,o)=\ell_1+\ell_2-\ell_3-\ell_4$
. Consequently, (174) and (175) yield, with s as in (175),
$\textsf{d}(\overline{U}_1,\overline{U}_2)-\textsf{d}(\overline{U}_3,o)=\ell_1+\ell_2-\ell_3-\ell_4$
. Consequently, (174) and (175) yield, with s as in (175),
 \begin{align} {\mathbb E{}}\,\bigl\lvert{\widehat{\Lambda_\textbf{e}}(\xi)}\bigr\rvert^2&= 3\int_{\mathbb R_+^5} e^{\textrm{i}\xi(\ell_1+\ell_2-\ell_3-\ell_4)} 2^6 s e^{-2s^2}\,\textrm{d}\ell_1\dotsm\,\textrm{d}\ell_5\notag\\&=192 \int_0^\infty \psi(s) s e^{-2s^2}\,\textrm{d} s,\end{align}
\begin{align} {\mathbb E{}}\,\bigl\lvert{\widehat{\Lambda_\textbf{e}}(\xi)}\bigr\rvert^2&= 3\int_{\mathbb R_+^5} e^{\textrm{i}\xi(\ell_1+\ell_2-\ell_3-\ell_4)} 2^6 s e^{-2s^2}\,\textrm{d}\ell_1\dotsm\,\textrm{d}\ell_5\notag\\&=192 \int_0^\infty \psi(s) s e^{-2s^2}\,\textrm{d} s,\end{align}
where, with
![]() $\Sigma_5(s)\,:\!=\,{\{{(\ell_1,\dots,\ell_5)\,:\,\ell_i>0 \text{ and } \ell_1+\dots+\ell_5=s}\}}$
,
$\Sigma_5(s)\,:\!=\,{\{{(\ell_1,\dots,\ell_5)\,:\,\ell_i>0 \text{ and } \ell_1+\dots+\ell_5=s}\}}$
,
We can easily find the Laplace transform of
![]() $\psi(s)$
: for
$\psi(s)$
: for
![]() $\lambda>0$
,
$\lambda>0$
,
 \begin{align} \int_0^\infty e^{-\lambda s}\psi(s)\,\textrm{d} s &= \int_{\mathbb R_+^5} e^{-\lambda(\ell_1+\dots+\ell_5)}e^{\textrm{i}\xi(\ell_1+\ell_2-\ell_3-\ell_4)}\,\textrm{d}\ell_1\dotsm\,\textrm{d}\ell_5\notag\\&=\frac{1}{(\lambda-\textrm{i}\xi)^2(\lambda+\textrm{i}\xi)^2\lambda}.\end{align}
\begin{align} \int_0^\infty e^{-\lambda s}\psi(s)\,\textrm{d} s &= \int_{\mathbb R_+^5} e^{-\lambda(\ell_1+\dots+\ell_5)}e^{\textrm{i}\xi(\ell_1+\ell_2-\ell_3-\ell_4)}\,\textrm{d}\ell_1\dotsm\,\textrm{d}\ell_5\notag\\&=\frac{1}{(\lambda-\textrm{i}\xi)^2(\lambda+\textrm{i}\xi)^2\lambda}.\end{align}
A partial fraction expansion of (178) yields,
for some coefficients
![]() $a(\xi),b_\pm(\xi),c_\pm(\xi)$
. It is easy to calculate these, but it suffices to note that (178) is homogeneous of degree
$a(\xi),b_\pm(\xi),c_\pm(\xi)$
. It is easy to calculate these, but it suffices to note that (178) is homogeneous of degree
![]() $-5$
in
$-5$
in
![]() $(\lambda,\xi)$
, and thus
$(\lambda,\xi)$
, and thus
![]() $a(\xi)=a\xi^{-4}$
,
$a(\xi)=a\xi^{-4}$
,
![]() $b_\pm(\xi)=b_\pm\xi^{-4}$
and
$b_\pm(\xi)=b_\pm\xi^{-4}$
and
![]() $c_\pm(\xi)=c_\pm\xi^{-3}$
for some complex
$c_\pm(\xi)=c_\pm\xi^{-3}$
for some complex
![]() $a,b_\pm,c_\pm$
. By inverting the Laplace transform (179), we find
$a,b_\pm,c_\pm$
. By inverting the Laplace transform (179), we find
Finally, we substitute (180) in (176). We define
and obtain, recalling (168),
We have
![]() $\hat h_1(\xi)=O(1)$
since
$\hat h_1(\xi)=O(1)$
since
![]() $h_1$
is integrable, and
$h_1$
is integrable, and
![]() $\xi\hat h_2(\xi)=\textrm{i}\widehat{h_2'}(\xi)=O(1)$
since
$\xi\hat h_2(\xi)=\textrm{i}\widehat{h_2'}(\xi)=O(1)$
since
![]() $h_2$
is differentiable with integrable derivative. Consequently, the result (170) follows.
$h_2$
is differentiable with integrable derivative. Consequently, the result (170) follows.
Remark 15.7. It is easy to see that in the proof above,
![]() $a=1$
and
$a=1$
and
![]() $\hat h_1(0)=\int_0^\infty s e^{-2s^2}\,\textrm{d} s=1/4$
; moreover,
$\hat h_1(0)=\int_0^\infty s e^{-2s^2}\,\textrm{d} s=1/4$
; moreover,
![]() $\hat h_1(\xi)=O(\xi^{-2})$
and
$\hat h_1(\xi)=O(\xi^{-2})$
and
![]() $\hat h_2(\xi)=O(\xi^{-3})$
. Hence, the proof yields
$\hat h_2(\xi)=O(\xi^{-3})$
. Hence, the proof yields
Thus, the estimate in Lemma 15.6 is sharp.
Remark 15.8. The result (170) (or (183)) can also be obtained in the same way from (172). However, for
![]() $k=4$
we have
$k=4$
we have
![]() $|\bar{\mathfrak{T}}^{4}|=5!!=15$
different shapes that we have to consider, and they yield several different terms in (176). The leading term in the partial fraction expansion (179) will now be
$|\bar{\mathfrak{T}}^{4}|=5!!=15$
different shapes that we have to consider, and they yield several different terms in (176). The leading term in the partial fraction expansion (179) will now be
![]() $a\xi^{-4}/\lambda^3$
.
$a\xi^{-4}/\lambda^3$
.
Proof of Theorem 15.5. Let
![]() $0<\alpha<3/2$
. Then, by Lemma 15.6,
$0<\alpha<3/2$
. Then, by Lemma 15.6,
 \begin{align} {\mathbb E{}} \int_{-\infty}^\infty \bigl\lvert{|\xi|^{\alpha}\widehat{\Lambda_\textbf{e}}(\xi)}\bigr\rvert^2\,\textrm{d}\xi&=2 \int_0^\infty |\xi|^{2\alpha}{\mathbb E{}}\,\bigl\lvert{\widehat{\Lambda_\textbf{e}}(\xi)}\bigr\rvert^2\,\textrm{d}\xi\notag\\&\leqslant C \int_0^1 \xi^{2\alpha}\,\textrm{d}\xi+ C\int_1^\infty \xi^{2\alpha-4}\,\textrm{d}\xi <\infty.\end{align}
\begin{align} {\mathbb E{}} \int_{-\infty}^\infty \bigl\lvert{|\xi|^{\alpha}\widehat{\Lambda_\textbf{e}}(\xi)}\bigr\rvert^2\,\textrm{d}\xi&=2 \int_0^\infty |\xi|^{2\alpha}{\mathbb E{}}\,\bigl\lvert{\widehat{\Lambda_\textbf{e}}(\xi)}\bigr\rvert^2\,\textrm{d}\xi\notag\\&\leqslant C \int_0^1 \xi^{2\alpha}\,\textrm{d}\xi+ C\int_1^\infty \xi^{2\alpha-4}\,\textrm{d}\xi <\infty.\end{align}
Hence, a.s., the function
![]() $\Lambda_\textbf{e}$
belongs to the (generalised) Sobolev space
$\Lambda_\textbf{e}$
belongs to the (generalised) Sobolev space
![]() ${\mathcal L}^2_{{\alpha}}$
(also called potential space; many different notations exist), which is defined as the space of all functions
${\mathcal L}^2_{{\alpha}}$
(also called potential space; many different notations exist), which is defined as the space of all functions
![]() $f\in L^2(\mathbb R)$
such that
$f\in L^2(\mathbb R)$
such that
see, e.g. [Reference Stein50, Chapter V] or [Reference Bergh and Löfström8, Chapter 6]. Furthermore, this Sobolev space equals the Besov space
![]() $B^{2,2}_{{\alpha}}$
, see again [Reference Stein50, Chapter V (there denoted
$B^{2,2}_{{\alpha}}$
, see again [Reference Stein50, Chapter V (there denoted
![]() $\Lambda_\alpha^{2,2}$
)] or [Reference Bergh and Löfström8, Chapter 6.]
$\Lambda_\alpha^{2,2}$
)] or [Reference Bergh and Löfström8, Chapter 6.]
![]() $B^{2,2}_{\alpha}$
is an
$B^{2,2}_{\alpha}$
is an
![]() $L^2$
version of
$L^2$
version of
![]() $\mathcal H_\alpha$
, and for
$\mathcal H_\alpha$
, and for
![]() $0<\alpha<1$
,
$0<\alpha<1$
,
![]() $B^{2,2}_{{\alpha}}$
may be defined as the set of functions in
$B^{2,2}_{{\alpha}}$
may be defined as the set of functions in
![]() $L^2$
such that
$L^2$
such that
the equivalence (within constant factors) of (186) with (185) follows easily from the Plancherel formula. (For a much more general result, see [Reference Bergh and Löfström8, Theorem 6.2.5] or [Reference Stein50, (V.60)].) For
![]() $1<\alpha<2$
, (177)) fails, but
$1<\alpha<2$
, (177)) fails, but
![]() $B^{2,2}_{\alpha}={\{{f\in L^2\,:\,f'\in B^{2,2}_{{\alpha-1}}}\}}$
, which again equals
$B^{2,2}_{\alpha}={\{{f\in L^2\,:\,f'\in B^{2,2}_{{\alpha-1}}}\}}$
, which again equals
![]() ${\mathcal L}^2_{\alpha}$
.
${\mathcal L}^2_{\alpha}$
.
If
![]() $1\leqslant\alpha<3/2$
, it follows that the derivative (in distribution sense)
$1\leqslant\alpha<3/2$
, it follows that the derivative (in distribution sense)
![]() $\Lambda_\textbf{e}'\in{\mathcal L}^2_{{\alpha-1}}$
. By the Sobolev (or Besov) embedding theorem [Reference Bergh and Löfström8, Theorem 6.5.1], see also [Reference Stein50, Theorem V.2] and, for a simplified version, [Reference Bousquet-Mélou and Janson14, Lemma 6.2], this implies
$\Lambda_\textbf{e}'\in{\mathcal L}^2_{{\alpha-1}}$
. By the Sobolev (or Besov) embedding theorem [Reference Bergh and Löfström8, Theorem 6.5.1], see also [Reference Stein50, Theorem V.2] and, for a simplified version, [Reference Bousquet-Mélou and Janson14, Lemma 6.2], this implies
![]() $\Lambda_\textbf{e}'\in L^p(\mathbb R)$
with
$\Lambda_\textbf{e}'\in L^p(\mathbb R)$
with
![]() $1/p = 1/2-(\alpha-1)$
. Since
$1/p = 1/2-(\alpha-1)$
. Since
![]() $\alpha$
may be chosen arbitrarily close to
$\alpha$
may be chosen arbitrarily close to
![]() $3/2$
, it follows that
$3/2$
, it follows that
![]() $\Lambda_\textbf{e}'\in L^p$
for every
$\Lambda_\textbf{e}'\in L^p$
for every
![]() $p<\infty$
. (Recall that
$p<\infty$
. (Recall that
![]() $\Lambda_\textbf{e}$
, and thus
$\Lambda_\textbf{e}$
, and thus
![]() $\Lambda_\textbf{e}'$
, has compact support, so small p is not a problem.) The continuous function
$\Lambda_\textbf{e}'$
, has compact support, so small p is not a problem.) The continuous function
![]() $\Lambda_\textbf{e}$
thus has a distributional derivative
$\Lambda_\textbf{e}$
thus has a distributional derivative
![]() $\Lambda_\textbf{e}'$
that is integrable, which implies that
$\Lambda_\textbf{e}'$
that is integrable, which implies that
![]() $\Lambda_\textbf{e}$
is the integral of this derivative, so
$\Lambda_\textbf{e}$
is the integral of this derivative, so
![]() $\Lambda_\textbf{e}$
is absolutely continuous, with a derivative in the usual sense a.e, which equals the distributional derivative
$\Lambda_\textbf{e}$
is absolutely continuous, with a derivative in the usual sense a.e, which equals the distributional derivative
![]() $\Lambda_\textbf{e}'$
.
$\Lambda_\textbf{e}'$
.
Finally,
![]() $\Lambda_\textbf{e}\in\mathcal H_\alpha$
for
$\Lambda_\textbf{e}\in\mathcal H_\alpha$
for
![]() $\alpha<1$
by
$\alpha<1$
by
![]() $\Lambda_\textbf{e}'\in L^p$
(with
$\Lambda_\textbf{e}'\in L^p$
(with
![]() $p=1/(1-\alpha)$
) and Hölder’s inequality, or directly by
$p=1/(1-\alpha)$
) and Hölder’s inequality, or directly by
![]() $\Lambda_\textbf{e}\in{\mathcal L}^2_{{\alpha+1/2}}=B^{2,2}_{{\alpha+1/2}}$
and the Besov embedding theorem [Reference Bergh and Löfström8, Theorem 6.5.1], [Reference Stein50, V.6.7], noting
$\Lambda_\textbf{e}\in{\mathcal L}^2_{{\alpha+1/2}}=B^{2,2}_{{\alpha+1/2}}$
and the Besov embedding theorem [Reference Bergh and Löfström8, Theorem 6.5.1], [Reference Stein50, V.6.7], noting
![]() $\mathcal H_\alpha=B^{\infty,\infty}_{{\alpha}}$
.
$\mathcal H_\alpha=B^{\infty,\infty}_{{\alpha}}$
.
Remark 15.9. For the Fourier transform
![]() $\widehat{L_\textbf{e}}$
, we have instead of (170) and (183) the analogous estimate
$\widehat{L_\textbf{e}}$
, we have instead of (170) and (183) the analogous estimate
and, more precisely,
These are proved by the same argument as above, now with
![]() $\bigl({d(\overline{U}_1,o)-d(\overline{U}_2,o)}\bigr)$
in the exponent in (173) and using (175) with
$\bigl({d(\overline{U}_1,o)-d(\overline{U}_2,o)}\bigr)$
in the exponent in (173) and using (175) with
![]() $k=2$
; we omit the details.
$k=2$
; we omit the details.
Note that the exponent of
![]() $\xi$
is
$\xi$
is
![]() $-2$
in (188), but
$-2$
in (188), but
![]() $-4$
in (174). Hence,
$-4$
in (174). Hence,
![]() $\widehat{\Lambda_\textbf{e}}(\xi)$
decays faster than
$\widehat{\Lambda_\textbf{e}}(\xi)$
decays faster than
![]() $\widehat{L_\textbf{e}}(\xi)$
(at least in an average sense), which intuitively means that
$\widehat{L_\textbf{e}}(\xi)$
(at least in an average sense), which intuitively means that
![]() $\Lambda_\textbf{e}$
is smoother than
$\Lambda_\textbf{e}$
is smoother than
![]() $L_\textbf{e}$
, as seen in the results above.
$L_\textbf{e}$
, as seen in the results above.
Note also that the result of Vervaat [Reference Vervaat51] mentioned in Remark 15.3 implies that
![]() $|\widehat{L_\textbf{e}}(\xi)|=|\widehat{{L}_{\textbf{b}}}(\xi)|$
. The expectation
$|\widehat{L_\textbf{e}}(\xi)|=|\widehat{{L}_{\textbf{b}}}(\xi)|$
. The expectation
![]() ${\mathbb E{}}|\widehat{{L}_{\textbf{b}}}(\xi)|^2$
can easily be calculated and estimated directly, since
${\mathbb E{}}|\widehat{{L}_{\textbf{b}}}(\xi)|^2$
can easily be calculated and estimated directly, since
![]() $\textbf{b}$
is a Gaussian process, which leads to another proof of (187) and (188); we leave the details to the reader.
$\textbf{b}$
is a Gaussian process, which leads to another proof of (187) and (188); we leave the details to the reader.
The proof above shows that
and thus
More precisely, it follows from the proof that
but not for any
![]() $\alpha\geqslant3/2$
.
$\alpha\geqslant3/2$
.
For comparison, (188) implies that
but not for
![]() $\alpha\geqslant\frac12$
. In this case, the range of
$\alpha\geqslant\frac12$
. In this case, the range of
![]() $\alpha$
in (192) is thus the same as the range of Hölder continuity, note that since
$\alpha$
in (192) is thus the same as the range of Hölder continuity, note that since
![]() $\mathcal H_\alpha=B^{\infty,\infty}_{\alpha}$
for
$\mathcal H_\alpha=B^{\infty,\infty}_{\alpha}$
for
![]() $\alpha\in(0,1)$
, this range equals the set of
$\alpha\in(0,1)$
, this range equals the set of
![]() $\alpha\in(0,1)$
such that
$\alpha\in(0,1)$
such that
![]() $L_\textbf{e}\in B^{\infty,\infty}_{\alpha}$
. Another, similar, example is the Brownian bridge
$L_\textbf{e}\in B^{\infty,\infty}_{\alpha}$
. Another, similar, example is the Brownian bridge
![]() $\textbf{b}$
; a simple calculation shows that
$\textbf{b}$
; a simple calculation shows that
![]() ${\mathbb E{}}\, \lVert{\textbf{b}}\rVert_{B^{2,2}_{{\alpha}}}^2<\infty$
for
${\mathbb E{}}\, \lVert{\textbf{b}}\rVert_{B^{2,2}_{{\alpha}}}^2<\infty$
for
![]() $\alpha<\frac12$
, but not for larger
$\alpha<\frac12$
, but not for larger
![]() $\alpha$
.
$\alpha$
.
This suggests (but does not prove) that
![]() $\Lambda_\textbf{e}$
is even smoother than shown by Theorem 15.5. However, the derivative
$\Lambda_\textbf{e}$
is even smoother than shown by Theorem 15.5. However, the derivative
![]() $\Lambda_\textbf{e}'$
is not Hölder continuous on
$\Lambda_\textbf{e}'$
is not Hölder continuous on
![]() $(-\infty,\infty)$
, as might be guessed from the analogy between (191) and (192). In fact, the (two-sided) derivative
$(-\infty,\infty)$
, as might be guessed from the analogy between (191) and (192). In fact, the (two-sided) derivative
![]() $\Lambda_\textbf{e}'$
does not exist at 0, and thus
$\Lambda_\textbf{e}'$
does not exist at 0, and thus
![]() $\Lambda_\textbf{e}'$
is not even continuous, at least not at 0.
$\Lambda_\textbf{e}'$
is not even continuous, at least not at 0.
Theorem 15.10.
![]() $\Lambda_{{\textbf{e}}}$
does not a.s. have a (two-sided) derivative at 0.
$\Lambda_{{\textbf{e}}}$
does not a.s. have a (two-sided) derivative at 0.
To see this, we note first the following.
Lemma 15.11. For every
![]() $x\geqslant0$
,
$x\geqslant0$
,
Proof. The result for
![]() $L_\textbf{e}$
is well known; it was shown by [Reference Chung15, (6.2)], and it is equivalent to the case
$L_\textbf{e}$
is well known; it was shown by [Reference Chung15, (6.2)], and it is equivalent to the case
![]() $k=1$
of (175).
$k=1$
of (175).
The result for
![]() $\Lambda_\textbf{e}$
follows by (24) and (23).
$\Lambda_\textbf{e}$
follows by (24) and (23).
Proof of Theorem 15.10. Suppose that
![]() $\Lambda_\textbf{e}$
is differentiable at 0. Since
$\Lambda_\textbf{e}$
is differentiable at 0. Since
![]() $\Lambda_\textbf{e}(x)=0$
for
$\Lambda_\textbf{e}(x)=0$
for
![]() $x<0$
, the derivative has to be 0, and thus
$x<0$
, the derivative has to be 0, and thus
![]() $\Lambda_\textbf{e}(x)/x\to0$
as
$\Lambda_\textbf{e}(x)/x\to0$
as
![]() $x\searrow0$
. Furthermore, Theorem 14.6 shows that
$x\searrow0$
. Furthermore, Theorem 14.6 shows that
![]() ${\mathbb E{}}\bigl({\Lambda_\textbf{e}(x)/x}\bigr)^2 \leqslant C$
, and thus
${\mathbb E{}}\bigl({\Lambda_\textbf{e}(x)/x}\bigr)^2 \leqslant C$
, and thus
![]() $\Lambda_\textbf{e}(x)/x$
is uniformly integrable for
$\Lambda_\textbf{e}(x)/x$
is uniformly integrable for
![]() $x>0$
. Consequently, if
$x>0$
. Consequently, if
![]() $\Lambda_\textbf{e}$
were a.s. differentiable at 0, then
$\Lambda_\textbf{e}$
were a.s. differentiable at 0, then
![]() ${\mathbb E{}}\bigl({\Lambda_\textbf{e}(x)/x}\bigr)\to0$
as
${\mathbb E{}}\bigl({\Lambda_\textbf{e}(x)/x}\bigr)\to0$
as
![]() $x\searrow0$
, which contradicts Lemma 15.11.
$x\searrow0$
, which contradicts Lemma 15.11.
Nevertheless, it is quite possible that
![]() $\Lambda_\textbf{e}$
is continuously differentiable on
$\Lambda_\textbf{e}$
is continuously differentiable on
![]() $[0,\infty)$
, with a one-sided derivative at 0. We end with some open problems suggested by the results above.
$[0,\infty)$
, with a one-sided derivative at 0. We end with some open problems suggested by the results above.
Problem 15.12.
-
(i) Is
 $\Lambda_\textbf{e}$
a.s. Lipschitz, i.e., is the derivative
$\Lambda_\textbf{e}$
a.s. Lipschitz, i.e., is the derivative
 $\Lambda_\textbf{e}'$
a.s. bounded?
$\Lambda_\textbf{e}'$
a.s. bounded? -
(ii) Does
 $\Lambda_\textbf{e}'(0)$
exist a.s. as a right derivative?
$\Lambda_\textbf{e}'(0)$
exist a.s. as a right derivative? -
(iii) Is the derivative
 $\Lambda_\textbf{e}'$
a.s. continuous on
$\Lambda_\textbf{e}'$
a.s. continuous on
 $[0,\infty)$
?
$[0,\infty)$
? -
(iv) Is the derivative
 $\Lambda_\textbf{e}'$
a.s. in
$\Lambda_\textbf{e}'$
a.s. in
 $\mathcal H_\alpha[0,\infty)$
for some
$\mathcal H_\alpha[0,\infty)$
for some
 $\alpha>0$
? For every
$\alpha>0$
? For every
 $\alpha<\frac12$
?
$\alpha<\frac12$
?
15.2. Finite n
We have in this section so far considered only the asymptotic profiles
![]() $L_\textbf{e}$
and
$L_\textbf{e}$
and
![]() $\Lambda_\textbf{e}$
. Consider now the profile
$\Lambda_\textbf{e}$
. Consider now the profile
![]() $L_n$
and distance profile
$L_n$
and distance profile
![]() $\Lambda_n$
of a conditioned Galton–Watson tree
$\Lambda_n$
of a conditioned Galton–Watson tree
![]() ${\mathcal T}^{{\textbf{p}}}_n$
, for a given offspring distribution
${\mathcal T}^{{\textbf{p}}}_n$
, for a given offspring distribution
![]() $\textbf{p}$
. We assume throughout the section that
$\textbf{p}$
. We assume throughout the section that
![]() $\mu(\textbf{p})=1$
and that
$\mu(\textbf{p})=1$
and that
![]() $0<\sigma^2(\textbf{p})<\infty$
; we will often add the condition that
$0<\sigma^2(\textbf{p})<\infty$
; we will often add the condition that
![]() $\textbf{p}$
has a finite fourth moment
$\textbf{p}$
has a finite fourth moment
![]() $\mu_4(\textbf{p})\,:\!=\,\sum_k k^4 p_k$
.
$\mu_4(\textbf{p})\,:\!=\,\sum_k k^4 p_k$
.
It was shown by Drmota and Gittenberger [Reference Drmota and Gittenberger18], see also [17, Theorem 4.24], that if the offspring distribution has an exponential moment, then
which by the standard argument in (147)–(148) yields
for
![]() $\alpha<1/4$
. This and Theorem 1.2 then yield (139) for
$\alpha<1/4$
. This and Theorem 1.2 then yield (139) for
![]() $\alpha<1/4$
. We conjecture that (194) can be extended to higher moments, yielding (195) and thus another proof of (15.1) for all
$\alpha<1/4$
. We conjecture that (194) can be extended to higher moments, yielding (195) and thus another proof of (15.1) for all
![]() $\alpha<\frac12$
, but this seems to require some non-trivial work.
$\alpha<\frac12$
, but this seems to require some non-trivial work.
Moreover, as said in [Reference Drmota17, footnote on p. 127], the proof of (194) does not really require an exponential moment, but it seems to require at least a fourth moment for the offspring distribution. We do not know whether such a moment condition really is necessary for (194), and we state the following problem.
Problem 15.13. Let
![]() $p\geqslant 2$
. Is it true for any offspring distribution
$p\geqslant 2$
. Is it true for any offspring distribution
![]() $\textbf{p}$
with
$\textbf{p}$
with
![]() $\mu(\textbf{p})=1$
and
$\mu(\textbf{p})=1$
and
![]() $\sigma^2(\textbf{p})<\infty$
then
$\sigma^2(\textbf{p})<\infty$
then
Is this true assuming a pth moment for
![]() $\textbf{p}$
? Assuming an exponential moment?
$\textbf{p}$
? Assuming an exponential moment?
Remark 15.14. A rerooting argument as in the proof of Theorem 14.1 shows that (196) would imply
Again we can ask under which conditions this holds.
We can also use generating functions and singularity analysis to estimate the Fourier transform of
![]() $L_{n}$
and
$L_{n}$
and
![]() $\Lambda_n$
. Recall that we in Section 2.1 have defined
$\Lambda_n$
. Recall that we in Section 2.1 have defined
![]() $L_n$
and
$L_n$
and
![]() $\Lambda_n$
as functions on
$\Lambda_n$
as functions on
![]() $\mathbb R$
, using linear interpolation. We first consider their restrictions to the integers, and the corresponding Fourier transforms, for
$\mathbb R$
, using linear interpolation. We first consider their restrictions to the integers, and the corresponding Fourier transforms, for
![]() $- \infty < \xi < \infty$
,
$- \infty < \xi < \infty$
,
 \begin{align} \widehat{L_n^\mathbb Z} (\xi)\,:\!=\, \sum_{k=0}^{\infty} L_{n}(k)e^{\textrm{i}\xi k}\ \text{and}\ {\widehat{\Lambda^\mathbb Z_n}}(\xi)\,:\!=\, \sum_{k=0}^{\infty} \Lambda_n(k)e^{\textrm{i} \xi k}.\end{align}
\begin{align} \widehat{L_n^\mathbb Z} (\xi)\,:\!=\, \sum_{k=0}^{\infty} L_{n}(k)e^{\textrm{i}\xi k}\ \text{and}\ {\widehat{\Lambda^\mathbb Z_n}}(\xi)\,:\!=\, \sum_{k=0}^{\infty} \Lambda_n(k)e^{\textrm{i} \xi k}.\end{align}
Note that these are periodic functions with period
![]() $2\pi$
, and that, as a consequence of (12) and (15),
$2\pi$
, and that, as a consequence of (12) and (15),
Lemma 15.15. Let
![]() ${\textbf{p}}$
be an offspring distribution with
${\textbf{p}}$
be an offspring distribution with
![]() $\mu({\textbf{p}})=1$
.
$\mu({\textbf{p}})=1$
.
-
(i) If
 $\textbf{p}$
has a finite second moment, then (200)
$\textbf{p}$
has a finite second moment, then (200) \begin{align} {\mathbb E{}}\, | \widehat{L_n^\mathbb Z}(\xi n^{-1/2}) |^{2}&\leqslant C n^{2}(\xi^{-2} \wedge 1), \qquad |\xi|\leqslant \pi n^{1/2}.\end{align}
\begin{align} {\mathbb E{}}\, | \widehat{L_n^\mathbb Z}(\xi n^{-1/2}) |^{2}&\leqslant C n^{2}(\xi^{-2} \wedge 1), \qquad |\xi|\leqslant \pi n^{1/2}.\end{align}
-
(ii) If
 $\textbf{p}$
has a finite fourth moment, then (201)
$\textbf{p}$
has a finite fourth moment, then (201) \begin{align}{\mathbb E{}}\,| \widehat{\Lambda^\mathbb Z_n}( \xi n^{-1/2}) |^{2}&\leqslant Cn^{4} (\xi^{-4} \wedge 1), \qquad |\xi|\leqslant \pi n^{1/2}.\end{align}
\begin{align}{\mathbb E{}}\,| \widehat{\Lambda^\mathbb Z_n}( \xi n^{-1/2}) |^{2}&\leqslant Cn^{4} (\xi^{-4} \wedge 1), \qquad |\xi|\leqslant \pi n^{1/2}.\end{align}
The proofs of (200) and (201) are based on lengthy calculations of some generating functions; we omit these and refer to the preprint version of the present paper [10, Appendix C].
We return to the interpolated profiles
![]() $L_n$
and
$L_n$
and
![]() $\Lambda_n$
and their Fourier transforms
$\Lambda_n$
and their Fourier transforms
![]() $\widehat{L_n}$
and
$\widehat{L_n}$
and
![]() $\widehat{\Lambda_n}$
defined by (168). It follows from (11) that
$\widehat{\Lambda_n}$
defined by (168). It follows from (11) that
and similarly
In particular,
![]() $|\widehat{L_n}(\xi)|\leqslant|\widehat{L_n^\mathbb Z}(\xi)|$
and
$|\widehat{L_n}(\xi)|\leqslant|\widehat{L_n^\mathbb Z}(\xi)|$
and
![]() $|\widehat{\Lambda_n}(\xi)|\leqslant|\widehat{\Lambda^\mathbb Z_n}(\xi)|$
; hence, the estimates in Lemma 15.15 hold also for
$|\widehat{\Lambda_n}(\xi)|\leqslant|\widehat{\Lambda^\mathbb Z_n}(\xi)|$
; hence, the estimates in Lemma 15.15 hold also for
![]() $\widehat{L_n}$
and
$\widehat{L_n}$
and
![]() $\widehat{\Lambda_n}$
.
$\widehat{\Lambda_n}$
.
We have stated Theorems 1.2 and 1.4 with convergence (in distribution) in
![]() $C[0,\infty]$
; however, it is obvious that then the same statement holds with convergence in
$C[0,\infty]$
; however, it is obvious that then the same statement holds with convergence in
![]() $C[\!-\infty,\infty]$
. Note that both sides of (1) and (3) are non-negative functions on
$C[\!-\infty,\infty]$
. Note that both sides of (1) and (3) are non-negative functions on
![]() $(-\infty,\infty)$
with integral 1. It is easily seen that in the set of such functions, convergence a.e. (and a fortiori convergence in
$(-\infty,\infty)$
with integral 1. It is easily seen that in the set of such functions, convergence a.e. (and a fortiori convergence in
![]() $C[\!-\infty,\infty]$
, i.e., uniform convergence) implies convergence in
$C[\!-\infty,\infty]$
, i.e., uniform convergence) implies convergence in
![]() $L^1(\mathbb R)$
, and thus (uniform) convergence of the Fourier transforms. Furthermore, the Fourier transforms of the left-hand sides of (1) and (3) are
$L^1(\mathbb R)$
, and thus (uniform) convergence of the Fourier transforms. Furthermore, the Fourier transforms of the left-hand sides of (1) and (3) are
![]() $n^{-1}\widehat{L_n}(\xi n^{-1/2})$
and
$n^{-1}\widehat{L_n}(\xi n^{-1/2})$
and
![]() $n^{-2}\widehat{\Lambda_n}(\xi n^{-1/2})$
, respectively. Hence, Theorems 1.2 and 1.4 imply that for any fixed
$n^{-2}\widehat{\Lambda_n}(\xi n^{-1/2})$
, respectively. Hence, Theorems 1.2 and 1.4 imply that for any fixed
![]() $\xi$
$\xi$
Consequently, by Fatou’s lemma, the estimates (200) and (201) in Lemma 15.15 yield another proof of the estimates (187) and (170) above.
Moreover, we can argue similarly to the proof of Theorem 15.5 and obtain a corresponding result on the smoothness of
![]() $\Lambda_n$
. Of course, this profile is by construction Lipschitz, but what is relevant is a smoothness estimate that is uniform in n.
$\Lambda_n$
. Of course, this profile is by construction Lipschitz, but what is relevant is a smoothness estimate that is uniform in n.
Theorem 15.16. If the offspring distribution
![]() ${\textbf{p}}$
has a finite fourth moment, then
${\textbf{p}}$
has a finite fourth moment, then
uniformly in n, for every fixed
![]() $\alpha<1$
.
$\alpha<1$
.
For the proof, we need a discrete version of (a simple case of) the Sobolev embedding theorem. We do not know an explicit reference, so for completeness, we state this and give a proof.
Lemma 15.17. Let
![]() $f\,:\,\mathbb R\to\mathbb R$
be a function initially defined on
$f\,:\,\mathbb R\to\mathbb R$
be a function initially defined on
![]() $\mathbb Z$
and extended by linear interpolation to
$\mathbb Z$
and extended by linear interpolation to
![]() $\mathbb R$
. Suppose that
$\mathbb R$
. Suppose that
![]() $\sum_{-\infty}^\infty|f(k)|<\infty$
, and define, as in (198),
$\sum_{-\infty}^\infty|f(k)|<\infty$
, and define, as in (198),
![]() $\widehat{f^\mathbb Z}(\xi)\,:\!=\,\sum_k f(k) e^{\textrm{i}\xi k}.$
Let
$\widehat{f^\mathbb Z}(\xi)\,:\!=\,\sum_k f(k) e^{\textrm{i}\xi k}.$
Let
![]() $0<\alpha<1$
. Then
$0<\alpha<1$
. Then
Proof. Let
![]() $j,k\in\mathbb Z$
. Then, by Fourier inversion,
$j,k\in\mathbb Z$
. Then, by Fourier inversion,
 \begin{align}|f(j)-f(k)|&=\left\lvert{\frac{1}{2\pi}\int_{-\pi}^{\pi}\bigl({e^{-\textrm{i} j\xi}-e^{-\textrm{i} k\xi}}\bigr)\widehat{f^\mathbb Z}(\xi)\,\textrm{d}\xi }\right\rvert\notag\\&\leqslant \int_{0}^{\pi}\bigl({|j-k|\xi \land1}\bigr)\bigl\lvert{\widehat{f^\mathbb Z}(\xi)}\bigr\rvert\,\textrm{d}\xi. \end{align}
\begin{align}|f(j)-f(k)|&=\left\lvert{\frac{1}{2\pi}\int_{-\pi}^{\pi}\bigl({e^{-\textrm{i} j\xi}-e^{-\textrm{i} k\xi}}\bigr)\widehat{f^\mathbb Z}(\xi)\,\textrm{d}\xi }\right\rvert\notag\\&\leqslant \int_{0}^{\pi}\bigl({|j-k|\xi \land1}\bigr)\bigl\lvert{\widehat{f^\mathbb Z}(\xi)}\bigr\rvert\,\textrm{d}\xi. \end{align}
Hence, using the Cauchy–Schwarz inequality,
Writing
![]() $M\,:\!=\,\int_0^{\pi} \bigl\lvert{\widehat{f^\mathbb Z}(\xi)}\bigr\rvert^2 \xi^{2\alpha+1}\,\textrm{d}\xi$
, and changing variables to
$M\,:\!=\,\int_0^{\pi} \bigl\lvert{\widehat{f^\mathbb Z}(\xi)}\bigr\rvert^2 \xi^{2\alpha+1}\,\textrm{d}\xi$
, and changing variables to
![]() $t\,:\!=\,|j-k|\xi$
in the first integral (assuming
$t\,:\!=\,|j-k|\xi$
in the first integral (assuming
![]() $j\neq k$
), we obtain
$j\neq k$
), we obtain
for some
![]() $C<\infty$
(depending on
$C<\infty$
(depending on
![]() $\alpha$
). Hence,
$\alpha$
). Hence,
whenever x and y are integers. Since f is linear between integers, it follows that (211) holds for all
![]() $x,y\in\mathbb R$
(with another C), i.e.,
$x,y\in\mathbb R$
(with another C), i.e.,
![]() $\lVert{{f}}\rVert_{\mathcal H_\alpha}\leqslant C M^{1/2}$
, as claimed in (207).
$\lVert{{f}}\rVert_{\mathcal H_\alpha}\leqslant C M^{1/2}$
, as claimed in (207).
Proof of Theorem 15.16. Lemma 15.17 and a change of variables together with (201) yield
 \begin{align}{\mathbb E{}}\,\lVert{{\Lambda_n}}\rVert_{\mathcal H_\alpha}^2&\leqslant C{\mathbb E{}} \int_{-\pi}^{\pi} |\xi|^{2\alpha+1} \bigl\lvert{\widehat{\Lambda^\mathbb Z_n}(\xi)}\bigr\rvert^2\,\textrm{d}\xi\notag\\&= C n^{-\alpha-1}\int_{-\pi n^{1/2}}^{\pi n^{1/2}} |\xi|^{2\alpha+1} {\mathbb E{}}\bigl\lvert{\widehat{\Lambda^\mathbb Z_n}(\xi n^{-1/2})}\bigr\rvert^2\,\textrm{d}\xi\notag\\&\leqslant C n^{3-\alpha}\int_{-\infty}^\infty \bigl({|\xi|^{2\alpha-3}\land |\xi|^{2\alpha+1}}\bigr)\,\textrm{d}\xi= C n^{3-\alpha}, \end{align}
\begin{align}{\mathbb E{}}\,\lVert{{\Lambda_n}}\rVert_{\mathcal H_\alpha}^2&\leqslant C{\mathbb E{}} \int_{-\pi}^{\pi} |\xi|^{2\alpha+1} \bigl\lvert{\widehat{\Lambda^\mathbb Z_n}(\xi)}\bigr\rvert^2\,\textrm{d}\xi\notag\\&= C n^{-\alpha-1}\int_{-\pi n^{1/2}}^{\pi n^{1/2}} |\xi|^{2\alpha+1} {\mathbb E{}}\bigl\lvert{\widehat{\Lambda^\mathbb Z_n}(\xi n^{-1/2})}\bigr\rvert^2\,\textrm{d}\xi\notag\\&\leqslant C n^{3-\alpha}\int_{-\infty}^\infty \bigl({|\xi|^{2\alpha-3}\land |\xi|^{2\alpha+1}}\bigr)\,\textrm{d}\xi= C n^{3-\alpha}, \end{align}
since the final integral converges for
![]() $0<\alpha<1$
. A change of variables yields (206).
$0<\alpha<1$
. A change of variables yields (206).
We end this subsection with a couple of open problems suggested by Theorem 15.16.
The fourth moment condition in Theorem 15.16 is used in our proof (see [Reference Berzunza Ojeda and Janson10]) of (201), but it seems likely that it can be weakened. Hence, we ask the following.
Problem 15.18. Does (206) hold assuming only a finite second moment for
![]() $\textbf{p}$
?
$\textbf{p}$
?
Just as for the limit
![]() $\Lambda_\textbf{e}$
, we do not know whether (206) holds for
$\Lambda_\textbf{e}$
, we do not know whether (206) holds for
![]() $\alpha=1$
. Since Hölder(1) equals Lipschitz, and
$\alpha=1$
. Since Hölder(1) equals Lipschitz, and
![]() $\Lambda_n$
is defined by linear interpolation, it is easy to see that
$\Lambda_n$
is defined by linear interpolation, it is easy to see that
Consequently, the question whether (206) holds for
![]() $\alpha=1$
is equivalent to the following. (Cf. (123).)
$\alpha=1$
is equivalent to the following. (Cf. (123).)
Problem 15.19. Assume that
![]() $\mu(\textbf{p})=1$
and that
$\mu(\textbf{p})=1$
and that
![]() $\textbf{p}$
has a finite second moment (or fourth moment, or an exponential moment). Is then
$\textbf{p}$
has a finite second moment (or fourth moment, or an exponential moment). Is then
A slightly weaker version is
16. Further remarks
Remark 16.1. In analogy with Sections 3 and 5, we might, as a third alternative, also define random unlabelled simply generated trees by using the weights (47) on the set
![]() $\mathfrak{U}_n$
of all unlabelled unrooted trees of order n. (These are defined as equivalence classes of labelled trees in
$\mathfrak{U}_n$
of all unlabelled unrooted trees of order n. (These are defined as equivalence classes of labelled trees in
![]() $\mathfrak{L}_n$
under isomorphisms.) It is usually more challenging to consider unlabelled trees; we conjecture that results similar to those above hold for unlabelled simply generated trees too, but we leave this as an open problem.
$\mathfrak{L}_n$
under isomorphisms.) It is usually more challenging to consider unlabelled trees; we conjecture that results similar to those above hold for unlabelled simply generated trees too, but we leave this as an open problem.
There is some existing work [Reference Ramzews and Stufler48, Reference Wang52] on yet another related model for random trees: simply generated unrooted plane trees (i.e., unlabelled unrooted trees where each vertex is endowed with a cyclic ordering of its neighbourhood). In particular, the results in [48, Sections 2 and 3] seem to be reminiscent of some of our results in Sections 3–5. Informally, through a series of approximations (using rooted/labelled/differently weighted versions) one ends up comparing those tree models to a pair of Galton–Watson trees (with the roots joined by an edge), conditioned on the sum of vertices. One of the two trees being typically macroscopic while the other is microscopic.
Remark 16.2. Another class of ‘simply generated’ trees is simply generated increasing trees, see [Reference Bergeron, Flajolet and Salvy7] and [Reference Drmota17, Section 1.3.3]. These random trees are quite different: They have (under weak conditions) logarithmic height; moreover, both the profile and distance profile are degenerate, in the sense that the distribution of depths or distances divided by
![]() $\log n$
converges to a point mass at some positive constant. With a more refined scaling, the profile and distance profile are both Gaussian, see Panholzer and Prodinger [Reference Panholzer and Prodinger45].
$\log n$
converges to a point mass at some positive constant. With a more refined scaling, the profile and distance profile are both Gaussian, see Panholzer and Prodinger [Reference Panholzer and Prodinger45].
Remark 16.3. The degenerate behaviour seen in Remark 16.2, with almost all distances close to
![]() $c\log n$
for some constant
$c\log n$
for some constant
![]() $c>0$
, seems to be typical for many classes of random trees with logarithmic height, see [Reference Janson31].
$c>0$
, seems to be typical for many classes of random trees with logarithmic height, see [Reference Janson31].
Problem 16.4. We have in this paper assumed that the offspring distribution is critical and has finite variance. It would be interesting to extend the results to the case of infinite variance, with the offspring distribution in the domain of attraction of a stable variable. In this case, the tree converges in a suitable sense to a random stable tree [Reference Duquesne20, Reference Kortchemski37]; moreover, there is a corresponding limit result for the profile [Reference Angtuncio and Bravo5, Reference Kersting34]. However, there seems to be several technical challenges to adapt the arguments above to this case, and we leave it as an open problem.
Acknowledgements
We thank Tom Hillegers for questions that inspired the present paper, and Stephan Wagner for helpful comments. GBO is supported by the Knut and Alice Wallenberg Foundation, a grant from the Swedish Research Council and The Swedish Foundations’ starting grant from the Ragnar Söderberg Foundation. SJ is supported by the Knut and Alice Wallenberg Foundation.
Appendix A. Tightness
We show here a general technical result used in the proof of Theorem 11.2, and thus of our main theorem.
We recall the standard criterion for tightness in
![]() $C{[0,1]}$
in, e.g., [11, Theorem 8.2], which we formulate as follows, using the modulus of continuity defined in (9). (The equivalence of our formulation and the one in [Reference Billingsley11] is a simple exercise.)
$C{[0,1]}$
in, e.g., [11, Theorem 8.2], which we formulate as follows, using the modulus of continuity defined in (9). (The equivalence of our formulation and the one in [Reference Billingsley11] is a simple exercise.)
Lemma A.1. A sequence of random functions
![]() $(X_n(t))_1^\infty$
in
$(X_n(t))_1^\infty$
in
![]() $C{[0,1]}$
is tight if and only if the following two conditions hold:
$C{[0,1]}$
is tight if and only if the following two conditions hold:
-
(i) The sequence
 $X_n(0)$
of random variables is tight.
$X_n(0)$
of random variables is tight. -
(ii)
 $\omega(\delta;\,X_n)\overset{\textrm{p}}{\longrightarrow}0$
as
$\omega(\delta;\,X_n)\overset{\textrm{p}}{\longrightarrow}0$
as
 $\delta\to0$
, uniformly in n.
$\delta\to0$
, uniformly in n.
The uniform convergence in probability in (ii) means that for every
![]() $\varepsilon,\eta>0$
, there exists
$\varepsilon,\eta>0$
, there exists
![]() $\delta>0$
such that
$\delta>0$
such that
Equivalently, for every sequence
![]() $\delta_k\to0$
and every sequence
$\delta_k\to0$
and every sequence
![]() $(n_k)_1^\infty$
,
$(n_k)_1^\infty$
,
We use this to prove the following general lemma on tightness of averages.
Lemma A.2. Suppose that
![]() $(X_n(t))_1^\infty$
is a sequence of random functions in
$(X_n(t))_1^\infty$
is a sequence of random functions in
![]() $C{[0,1]}$
, that
$C{[0,1]}$
, that
![]() $(N_n)_1^\infty$
is an arbitrary sequence of positive integers, and that for each n,
$(N_n)_1^\infty$
is an arbitrary sequence of positive integers, and that for each n,
![]() $(X_{ni}(t))_{i=1}^{N_n}$
is a, possibly dependent, family of identically distributed random functions with
$(X_{ni}(t))_{i=1}^{N_n}$
is a, possibly dependent, family of identically distributed random functions with
![]() $X_{ni}\overset{{d}}{=} X_n$
. Assume that
$X_{ni}\overset{{d}}{=} X_n$
. Assume that
-
(i) The sequence
 $(X_n)$
is tight in
$(X_n)$
is tight in
 $C{[0,1]}$
.
$C{[0,1]}$
. -
(ii) The sequence of random variables
(A3)is uniformly integrable. \begin{align} \lVert{X_n}\rVert\,:\!=\,\sup_{t\in{[0,1]}}|X_n(t)| \end{align}
\begin{align} \lVert{X_n}\rVert\,:\!=\,\sup_{t\in{[0,1]}}|X_n(t)| \end{align}
Then the sequence of averages
 \begin{align} Y_n(t)\,:\!=\,\frac{1}{N_n}\sum_{i=1}^{N_n} X_{ni}(t)\end{align}
\begin{align} Y_n(t)\,:\!=\,\frac{1}{N_n}\sum_{i=1}^{N_n} X_{ni}(t)\end{align}
is tight in
![]() $C{[0,1]}$
.
$C{[0,1]}$
.
Remark A.3. We state Lemma A.2 for
![]() $C{[0,1]}$
; it transfers immediately to, e.g.,
$C{[0,1]}$
; it transfers immediately to, e.g.,
![]() $C[0,\infty]$
. It follows also that the lemma holds for
$C[0,\infty]$
. It follows also that the lemma holds for
![]() $C[0,\infty)$
, with (ii) replaced by the assumption that
$C[0,\infty)$
, with (ii) replaced by the assumption that
![]() $\sup_{[0,b]}|X_n|$
over any finite interval [0,b] is uniformly integrable.
$\sup_{[0,b]}|X_n|$
over any finite interval [0,b] is uniformly integrable.
Proof. Let
![]() $\delta_k\to0$
and let
$\delta_k\to0$
and let
![]() $n_k$
be arbitrary positive integers. Then (A2) holds by assumption (i) and Lemma A.1.
$n_k$
be arbitrary positive integers. Then (A2) holds by assumption (i) and Lemma A.1.
Furthermore, for any
![]() $\delta>0$
, we obviously have, by (9),
$\delta>0$
, we obviously have, by (9),
![]() $\omega(\delta;\,X_n)\leqslant2\lVert{X_n}\rVert$
. In particular,
$\omega(\delta;\,X_n)\leqslant2\lVert{X_n}\rVert$
. In particular,
![]() $\omega(\delta_k;\,X_{n_k})\leqslant2\lVert{X_{n_k}}\rVert$
, and it follows from (ii) that the sequence
$\omega(\delta_k;\,X_{n_k})\leqslant2\lVert{X_{n_k}}\rVert$
, and it follows from (ii) that the sequence
![]() $\omega(\delta_k;\,X_{n_k})$
,
$\omega(\delta_k;\,X_{n_k})$
,
![]() $k\geqslant1$
, is uniformly integrable. Hence, (A2) implies
$k\geqslant1$
, is uniformly integrable. Hence, (A2) implies
Next, it follows from the definitions (A4) and (9) that, for any
![]() $\delta>0$
,
$\delta>0$
,
 \begin{align} \omega({\delta;\,Y_n})=\frac{1}{N_n}\omega\Bigl({\delta;\,\sum_{i=1}^{N_n}X_{ni}}\Bigr)\leqslant\frac{1}{N_n}\sum_{i=1}^{N_n}\omega\bigl({\delta;\,X_{ni}}\bigr)\end{align}
\begin{align} \omega({\delta;\,Y_n})=\frac{1}{N_n}\omega\Bigl({\delta;\,\sum_{i=1}^{N_n}X_{ni}}\Bigr)\leqslant\frac{1}{N_n}\sum_{i=1}^{N_n}\omega\bigl({\delta;\,X_{ni}}\bigr)\end{align}
and hence,
 \begin{align}{\mathbb E{}} \omega({\delta;\,Y_n})\leqslant\frac{1}{N_n}\sum_{i=1}^{N_n}{\mathbb E{}}\omega\bigl({\delta;\,X_{ni}}\bigr)={\mathbb E{}}\omega\bigl({\delta;\,X_{n}}\bigr).\end{align}
\begin{align}{\mathbb E{}} \omega({\delta;\,Y_n})\leqslant\frac{1}{N_n}\sum_{i=1}^{N_n}{\mathbb E{}}\omega\bigl({\delta;\,X_{ni}}\bigr)={\mathbb E{}}\omega\bigl({\delta;\,X_{n}}\bigr).\end{align}
Consequently, by (A5) and (A7),
Since the sequences
![]() $(\delta_k)_k$
and
$(\delta_k)_k$
and
![]() $(n_k)_k$
are arbitrary, this shows that the sequence
$(n_k)_k$
are arbitrary, this shows that the sequence
![]() $(Y_n)_n$
satisfies (A2) and thus condition Lemma A.1(ii).
$(Y_n)_n$
satisfies (A2) and thus condition Lemma A.1(ii).
Furthermore, condition Lemma A.1(i) holds too, because by (A4), (A3) and assumption (ii),
 \begin{align} {\mathbb E{}}|Y_n(0)|\leqslant\frac{1}{N_n}\sum_{i=1}^{N_n}{\mathbb E{}}| X_{ni}(0)|={\mathbb E{}}|X_n(0)|\leqslant{\mathbb E{}}\,\lVert{X_n}\rVert=O(1),\end{align}
\begin{align} {\mathbb E{}}|Y_n(0)|\leqslant\frac{1}{N_n}\sum_{i=1}^{N_n}{\mathbb E{}}| X_{ni}(0)|={\mathbb E{}}|X_n(0)|\leqslant{\mathbb E{}}\,\lVert{X_n}\rVert=O(1),\end{align}
which implies that the sequence
![]() $Y_n(0)$
is tight. Hence, the conclusion follows by Lemma A.1.
$Y_n(0)$
is tight. Hence, the conclusion follows by Lemma A.1.
Remark A.4. The assumption on uniform integrability in Lemma A.2(ii) cannot be weakened to
![]() ${\mathbb E{}}\,\lVert{X_n}\rVert=O(1)$
. For an example, let
${\mathbb E{}}\,\lVert{X_n}\rVert=O(1)$
. For an example, let
where
![]() $\xi_n\sim{Be}(1/n)$
, i.e.,
$\xi_n\sim{Be}(1/n)$
, i.e.,
![]() ${\mathbb P{}}(\xi_n=1)=1/n$
and otherwise
${\mathbb P{}}(\xi_n=1)=1/n$
and otherwise
![]() $\xi_n=0$
. Then
$\xi_n=0$
. Then
![]() ${\mathbb E{}}\,\lVert{X_n}\rVert=1$
. On the other hand, take
${\mathbb E{}}\,\lVert{X_n}\rVert=1$
. On the other hand, take
![]() $N_n\,:\!=\,n$
and let
$N_n\,:\!=\,n$
and let
![]() $X_{ni}\overset{\textrm{d}}{=} X_n$
be independent,
$X_{ni}\overset{\textrm{d}}{=} X_n$
be independent,
![]() $1\leqslant i\leqslant N_n$
. Then, for every n, with probability
$1\leqslant i\leqslant N_n$
. Then, for every n, with probability
![]() $e^{-1}+o(1)$
exactly one
$e^{-1}+o(1)$
exactly one
![]() $X_{ni}$
is not identically 0, and in this case
$X_{ni}$
is not identically 0, and in this case
![]() $Y_n=(1\land nt)$
and thus
$Y_n=(1\land nt)$
and thus
![]() $\omega(1/n;\,Y_n)=1$
. Hence,
$\omega(1/n;\,Y_n)=1$
. Hence,
![]() ${\mathbb P{}}\bigl({\omega(1/n;\,Y_n)=1}\bigr) \geqslant e^{-1}+o(1)$
and thus (A2) and Lemma A.1(ii) do not hold for
${\mathbb P{}}\bigl({\omega(1/n;\,Y_n)=1}\bigr) \geqslant e^{-1}+o(1)$
and thus (A2) and Lemma A.1(ii) do not hold for
![]() $(Y_n)$
; thus, the sequence
$(Y_n)$
; thus, the sequence
![]() $Y_n$
is not tight.
$Y_n$
is not tight.